น้อง ๆ หลายคนอาจเคยได้ยินคำว่า “ความคล้าย” กันมาบ้างแล้วในชีวิตประจำวัน แต่พอขึ้น ม.3 ก็จะเห็นว่ามีบทเรียนเรื่องความคล้ายอยู่ในเนื้อหาคณิต ม.3 ด้วย สงสัยกันมั้ยว่าในทางคณิตศาสตร์นั้น ความคล้ายคืออะไร ?
วันนี้พี่ก็เลยจะมาสรุปเรื่อง ความคล้าย ม.3 เพื่อให้น้อง ๆ ที่กำลังเรียนอยู่ชั้น ม.3 ได้เข้าใจเรื่องนี้มากขึ้น แต่ใครที่กำลังเรียนอยู่ชั้น ม.2 เตรียมตัวขึ้น ม.3 ก็มาทำความเข้าใจไปพร้อมกันได้น้าา
ความคล้ายคืออะไร ?
ถ้าน้อง ๆ ลองดูสิ่งของรอบตัว ก็จะเจอว่ามีสิ่งของเครื่องใช้หลายอย่างที่มีรูปร่างคล้ายกัน แต่ต่างกันที่ขนาด เช่น ทีวี กล่องเก็บอาหาร แก้วน้ำ ตุ๊กตาแม่ลูกดกหรือมาโตรชก้า เป็นต้น เราจะเรียกสิ่งของที่มีรูปร่างคล้ายกันเหล่านี้ว่าเป็นสิ่งของที่คล้ายกัน
ซึ่งในบทเรียนนี้ไม่ได้กล่าวถึงเพียงรูปสามเหลี่ยมที่คล้ายกันเท่านั้น สังเกตได้จากชื่อบทเลย เพราะชื่อบทไม่ได้พูดแค่ว่าเป็นบทเกี่ยวกับรูปสามเหลี่ยมที่คล้ายกัน แต่พูดมาเป็นคำกว้าง ๆ คือ “ความคล้าย” ดังนั้นในบทนี้กล่าวถึงรูปเรขาคณิตที่มีรูปร่างคล้ายกันด้วยเช่นกันนะ ให้น้อง ๆ ลองพิจารณารูปของรูปเรขาคณิตต่อไปนี้
ตัวอย่างที่ 1 พิจารณารูปเรขาคณิตที่คล้ายกัน
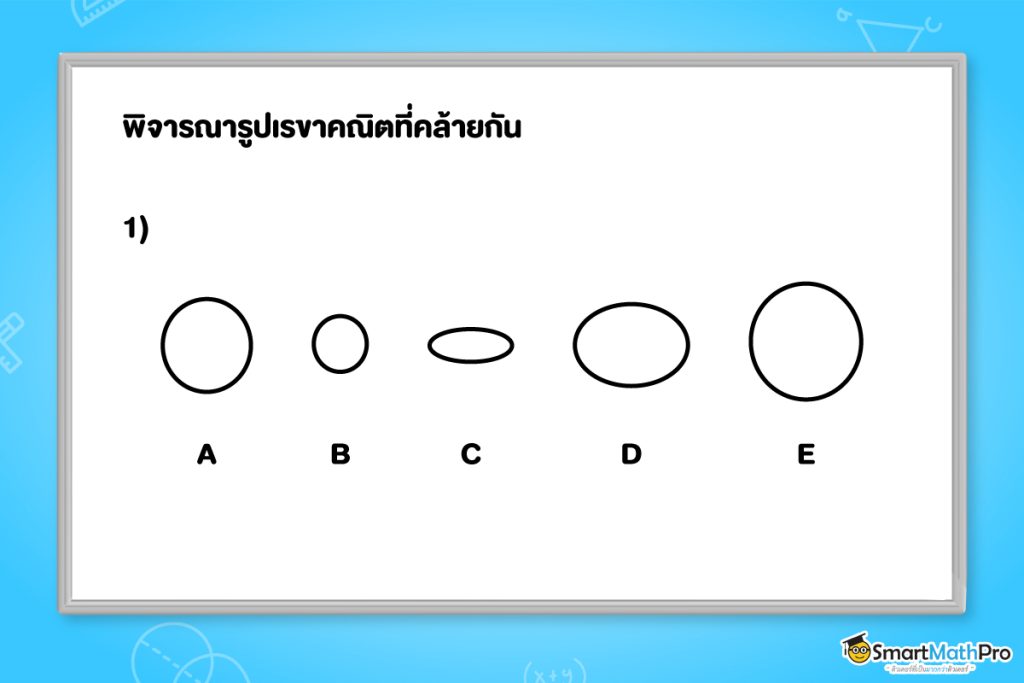
จะเห็นว่ารูป A, B และ E เป็นรูปวงกลมที่มีขนาดต่างกัน แต่รูป C และ D เป็นรูปวงรี ซึ่งมีรูปร่างและขนาดต่างกัน
จะเห็นว่ารูป B, C และ E เป็นรูปห้าเหลี่ยมที่มีลักษณะคล้ายกัน แต่มีขนาดต่างกัน แต่รูป A และ D เป็นรูปห้าเหลี่ยมที่มีรูปร่างและขนาดต่างกัน ดังนั้น รูป B, C และ E เป็นรูปเรขาคณิตที่คล้ายกัน
เราจึงสรุปได้ว่า รูปเรขาคณิตสองรูปเป็นรูปที่คล้ายกัน เมื่อรูปเรขาคณิตทั้งสองนั้นมีรูปร่างเหมือนกัน โดยรูปเรขาคณิตที่คล้ายกันอาจมีขนาดเท่ากันหรือแตกต่างกันก็ได้
สัญลักษณ์
รูปเรขาคณิต A และรูปเรขาคณิต B เป็นรูปที่คล้ายกัน จะเขียนแทนว่า รูปเรขาคณิต A \sim รูปเรขาคณิต B
สมบัติของความคล้าย
- สมบัติสะท้อน:
รูปเรขาคณิต A \sim รูปเรขาคณิต A - สมบัติสมมาตร:
ถ้ารูปเรขาคณิต A \sim รูปเรขาคณิต B
แล้วรูปเรขาคณิต B \sim รูปเรขาคณิต A - สมบัติถ่ายทอด:
ถ้ารูปเรขาคณิต A \sim รูปเรขาคณิต B
และรูปเรขาคณิต B \sim รูปเรขาคณิต C
แล้วรูปเรขาคณิต A \sim รูปเรขาคณิต C
บทนิยาม
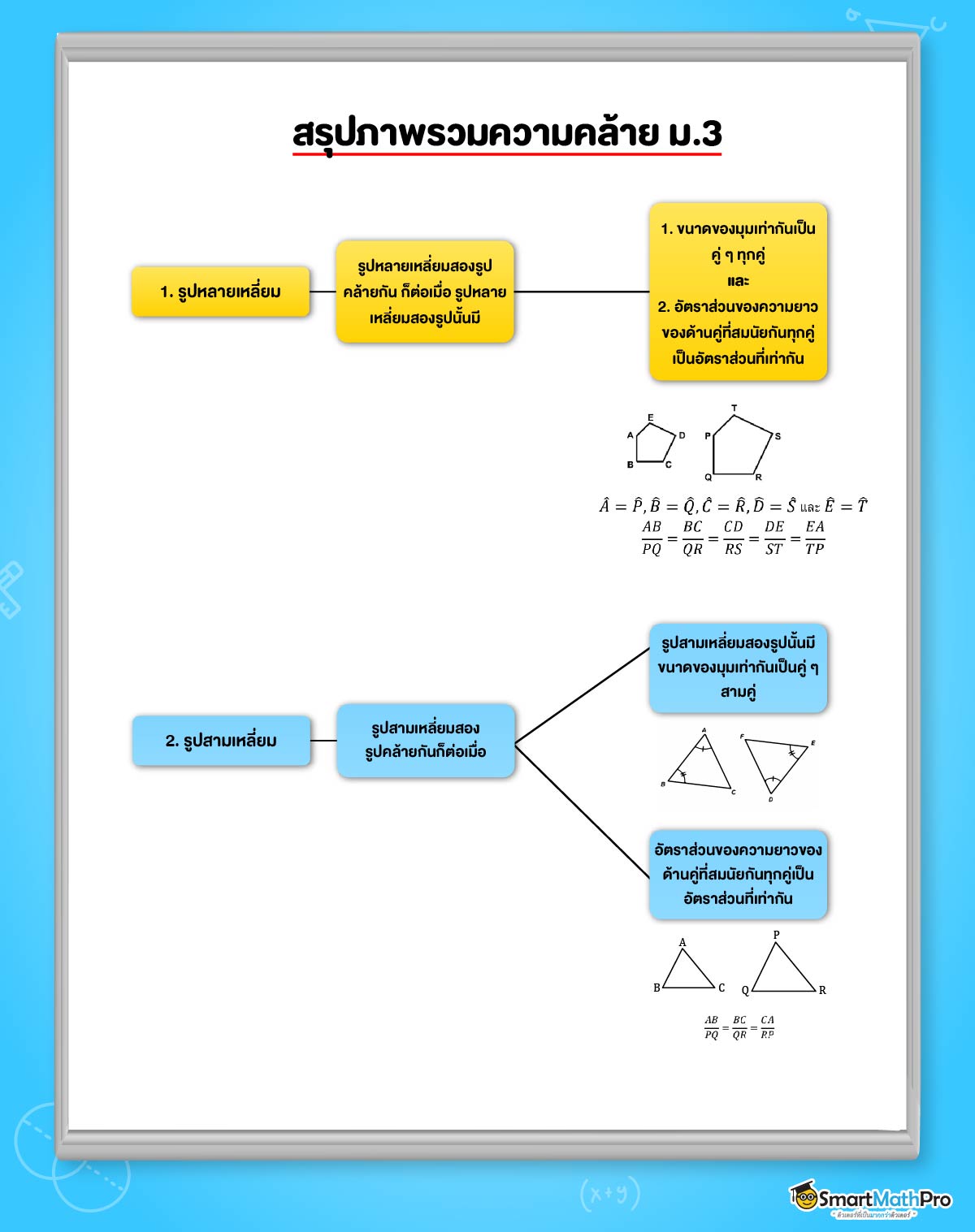
รูปหลายเหลี่ยมสองรูปคล้ายกัน ก็ต่อเมื่อ รูปหลายเหลี่ยมสองรูปนั้นมี
1. ขนาดของมุมเท่ากันเป็นคู่ ๆ ทุกคู่
และ
2. อัตราส่วนของความยาวของด้านคู่ที่สมนัยกันทุกคู่เป็นอัตราส่วนที่เท่ากัน
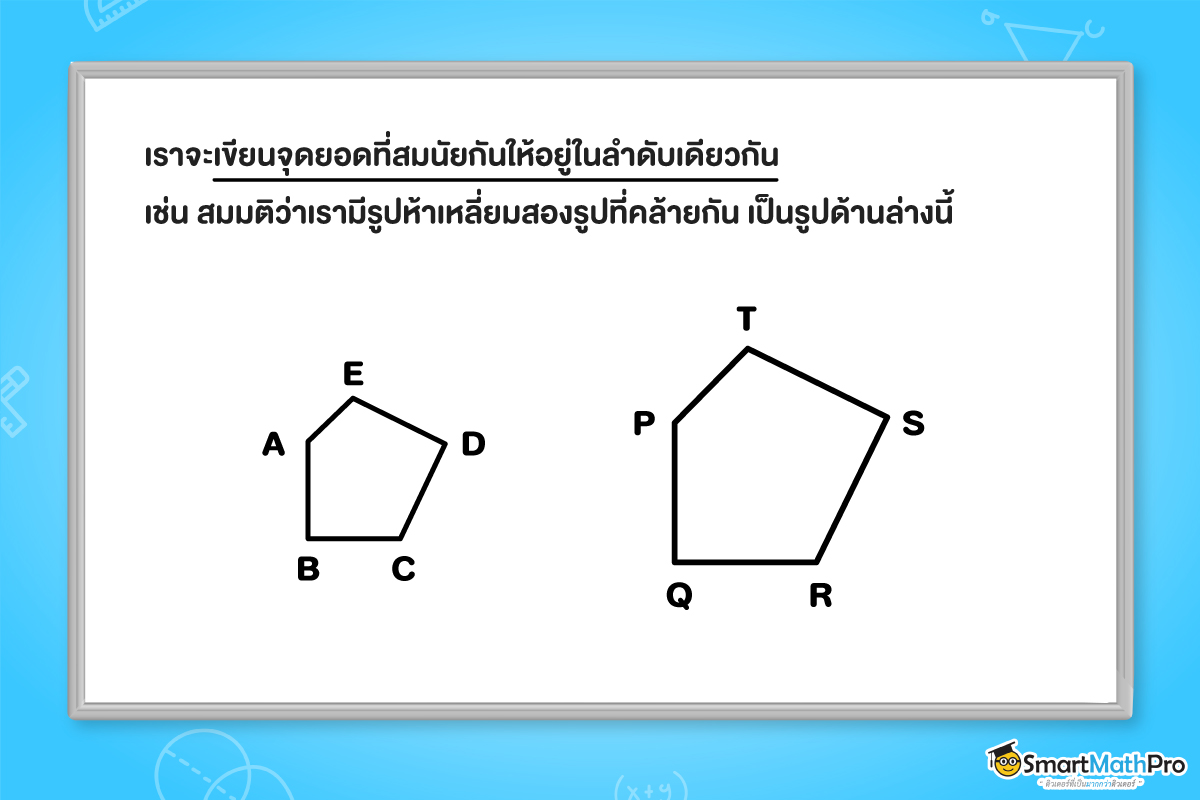
ถ้าน้อง ๆ ต้องการเขียนว่ารูปห้าเหลี่ยมทั้งสองคล้ายกัน ให้น้อง ๆ เขียนโดยเรียงลำดับมุมคู่ที่สมนัยกันแล้วเรียงลำดับไปยังมุมที่อยู่ติดกัน (ในทิศทวนหรือตามเข็มนาฬิกาก็ได้)
จากรูปเราพอจะเห็นว่า \hat{A}=\hat{P},\ \hat{B}=\hat{Q},\ \hat{C}=\hat{R},\ \hat{D}=\hat{S} และ \hat{E}=\hat{T}
เราจะได้ว่ามุมแต่ละคู่ที่มีขนาดเท่ากันเหล่านั้นคือมุมคู่ที่สมนัยกัน
ดังนั้น เราจะเขียนเป็นสัญลักษณ์ได้ว่า รูป ABCDE \sim รูป PQRST
เราจะไม่นิยมเขียนเรียงแบบอื่นที่มุมคู่สมนัยกันอยู่ไม่ตรงกันน้า
ตัวอย่างที่ 2 รูปสี่เหลี่ยมที่กำหนดให้ เป็นรูปสี่เหลี่ยมที่คล้ายกันหรือไม่ เพราะเหตุใด
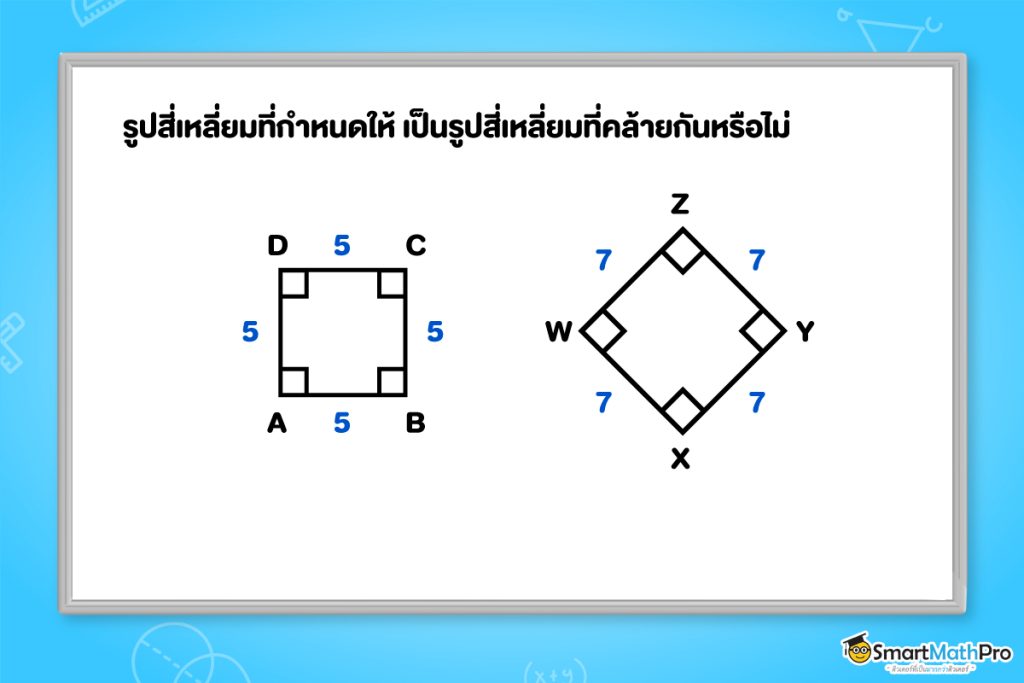
แนวคิด ใช้บทนิยามทั้ง 2 ข้อมาตรวจสอบว่ารูปสี่เหลี่ยมทั้งสองคล้ายกันหรือไม่
วิธีทำ จากรูป น้อง ๆ จะเห็นว่ารูปสี่เหลี่ยมทั้งสองรูป เป็นรูปสี่เหลี่ยมที่มีมุมฉากทั้งหมดเลย
ดังนั้น มุมของรูปสี่เหลี่ยมทั้งสองรูปจะเท่ากันเป็นคู่ ๆ ทุกคู่
พิจารณาอัตราส่วนของความยาวด้านคู่ที่สมนัยกัน
จะได้ว่า \frac{AB}{WX}=\frac{BC}{XY}=\frac{CD}{YZ}=\frac{DA}{ZW}=\frac{5}{7}
ดังนั้น \square ABCD \sim \square WXYZ
รูปสามเหลี่ยมที่คล้ายกัน
จากที่เรารู้จักรูปหลายเหลี่ยมที่คล้ายกันในหัวข้อก่อนหน้า นั่นยังไม่ใช่หัวข้อหลักเลยน้าา หัวข้อหลักของบทความคล้ายอยู่ที่หัวข้อนี้เลย นั่นคือเรื่อง “รูปสามเหลี่ยมที่คล้ายกัน” ข้อสอบก็จะออกเกี่ยวกับหัวข้อนี้เป็นหลัก แถมยังออกสอบเยอะกว่าหัวข้ออื่นมาก ๆ อีกด้วยน้า
ซึ่งในหัวข้อนี้เราจะนำบทนิยามของรูปหลายเหลี่ยมที่คล้ายกันมาช่วยพิจารณาความคล้ายกันของรูปสามเหลี่ยมด้วยนะ เป็นตามตัวอย่างต่อไปนี้เลย
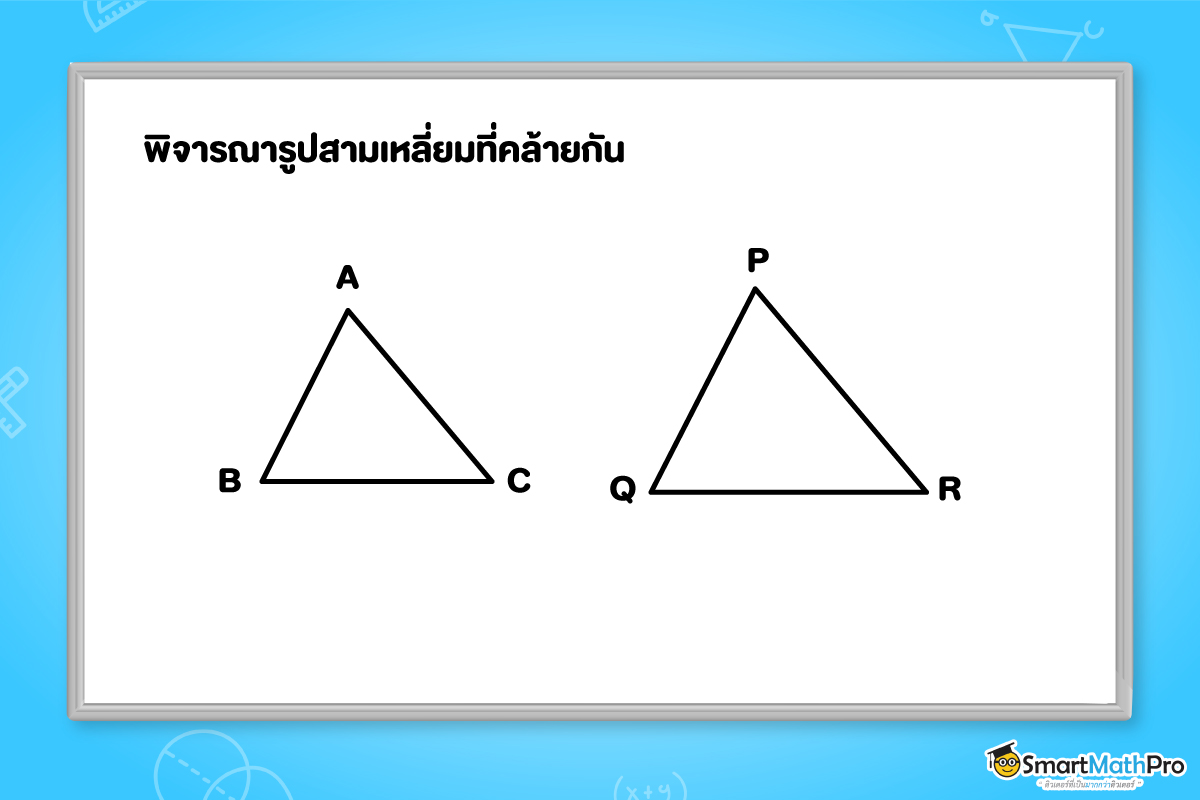
จากบทนิยามของรูปหลายเหลี่ยมที่คล้ายกัน \Delta ABC\sim\Delta PQR ก็ต่อเมื่อ
1. \hat{A}=\hat{P},\ \hat{B}=\hat{Q}\ และ \hat{C}=\hat{R}
นั่นคือ ขนาดของมุมเท่ากันเป็นคู่ ๆ ทุกคู่
และ
2. \frac{AB}{PQ}=\frac{BC}{QR}=\frac{CA}{RP}
นั่นคือ อัตราส่วนของความยาวของด้านคู่ที่สมนัยกันทุกคู่เป็นอัตราส่วนที่เท่ากัน
หลักการพิจารณารูปสามเหลี่ยมที่คล้ายกัน
น้อง ๆ บางคนอาจสงสัยว่าแล้วเราต้องพิจารณาทั้งสองข้อตามบทนิยามของรูปหลายเหลี่ยมที่คล้ายกันเลยไหม เพื่อที่จะสรุปว่ารูปสามเหลี่ยมที่เรากำลังพิจารณาอยู่มันคล้ายกันหรือไม่ เวลาเราแก้โจทย์เรามักจะไม่พิจารณาตามบทนิยามจนครบทั้งสองข้อแล้วค่อยสรุปคำตอบนะ เพราะโดยทั่วไป ถ้ารูปสามเหลี่ยมสองรูปมีขนาดของมุมเท่ากันเป็นคู่ ๆ สามคู่ แล้วอัตราส่วนของความยาวของด้าน คู่ที่สมนัยกันทั้งสามคู่จะเท่ากันตามไปด้วย
นั่นคือ แค่เราพิจารณารูปสามเหลี่ยมสองรูปว่ามีขนาดของมุมเท่ากันเป็นคู่ ๆ สามคู่ ก็เป็นเงื่อนไขที่เพียงพอแล้วที่จะทำให้สรุปได้ว่า รูปสามเหลี่ยมสองรูปนั้นเป็นรูปสามเหลี่ยมที่คล้ายกัน โดยที่เราไม่จำเป็นต้องตรวจสอบอัตราส่วนของความยาวของด้านคู่ที่สมนัยกันเหมือนรูปหลายเหลี่ยมอื่น ๆ ในทางคณิตศาสตร์ได้ให้บทนิยามของรูปสามเหลี่ยมที่คล้ายกัน ดังนี้
บทนิยาม รูปสามเหลี่ยมสองรูปคล้ายกัน ก็ต่อเมื่อ รูปสามเหลี่ยมสองรูปนั้น มีขนาดของมุมเท่ากันเป็นคู่ ๆ สามคู่
ตัวอย่างที่ 3 รูปสามเหลี่ยมที่กำหนดให้ เป็นรูปสามเหลี่ยมที่คล้ายกันหรือไม่ เพราะเหตุใด
พิจารณาโดยใช้บทนิยามข้างต้น จะได้ว่า \Delta RAT \sim\Delta DOG เพราะ มีมุมที่มีขนาดเท่ากันเป็นคู่ ๆ สามคู่
คือ \hat{R}=\hat{D} , \ \hat{A} = \hat{O}\ และ \hat{T} = \hat{G}
นอกจากบทนิยามข้างต้น ที่กล่าวถึงการที่สามเหลี่ยมจะเป็นสามเหลี่ยมคล้ายได้ถ้าเราพิจารณาแล้วพบว่ามีมุมเท่ากันป็นคู่ ๆ ทั้งสามคู่แล้ว ยังมีทฤษฎีบทต่อไปนี้ ที่กล่าวถึงอัตราส่วนของด้านคู่ที่สมนัยกันอีกด้วย นั่นคือ
ทฤษฎีบท ถ้าอัตราส่วนของความยาวของด้านคู่ที่สมนัยกันทุกคู่ของรูปสามเหลี่ยมสองรูปเป็นอัตราส่วนที่เท่ากันแล้วรูปสามเหลี่ยมสองรูปนั้นเป็นรูปสามเหลี่ยมที่คล้ายกัน
ตัวอย่างที่ 4 รูปสามเหลี่ยมที่กำหนดให้ต่อไปนี้ เป็นรูปสามเหลี่ยมที่คล้ายกันหรือไม่ เพราะเหตุใด
พิจารณาโดยใช้ทฤษฎีบทข้างต้น จะได้ว่า
\frac{AC}{EH}=\frac{8}{16}=\frac{1}{2}
\frac{CT}{HN}=\frac{13}{26}=\frac{1}{2}
\frac{TA}{NE}=\frac{10}{20}=\frac{1}{2}
ดังนั้น \Delta CAT \sim\Delta HEN
จากบทนิยามและทฤษฎีบทเกี่ยวกับรูปสามเหลี่ยมที่คล้ายกัน และจากตัวอย่างที่ 3 และ 4 ที่ผ่านมา จะเห็นว่า เราสามารถใช้เพียงบทนิยาม หรือใช้เพียงทฤษฎีบทเพียงอย่างเดียวเพื่อตรวจสอบรูปสามเหลี่ยมที่คล้ายกันได้
ดังนั้นต่อจากนี้ ถ้าน้อง ๆ จะทำโจทย์ในบทนี้ต่อไป ให้ใช้เพียงเงื่อนไขเดียว จากสองเงื่อนไขเพื่อพิจารณาได้ว่ารูปสามเหลี่ยมที่โจทย์กำหนดให้คล้ายกันหรือไม่ก็เพียงพอแล้วนะ ซึ่งเงื่อนไขที่น้อง ๆ สามารถเลือกใช้เพื่อตรวจสอบได้ คือ
1. รูปสามเหลี่ยมทั้งสองรูปมีขนาดของมุมเท่ากันเป็นคู่ๆ ทั้งสามคู่
หรือ
2. อัตราส่วนของความยาวด้านของคู่ที่สมนัยกันทุกคู่ เป็นอัตราส่วนที่เท่ากัน
ถึงตรงนี้พี่คิดว่าน้อง ๆ น่าจะเข้าใจเกี่ยวกับรูปสามเหลี่ยมที่คล้ายกันแล้ว เรานำความรู้ที่ได้ในหัวข้อก่อนหน้านี้มาแก้โจทย์ในตัวอย่างต่อไปนี้กัน แต่ขอเตือนน้อง ๆ น้าา ว่าทุกครั้ง ก่อนที่เราจะใช้เงื่อนไขข้อใดข้อหนึ่งในการแก้ปัญหาโจทย์ปัญหาเกี่ยวกับรูปสามเหลี่ยมที่คล้ายกัน เราต้องตรวจสอบก่อนเสมอว่ารูปสามเหลี่ยมสองรูปนั้นคล้ายกันใช่ไหมนะ
ถ้ารูปสามเหลี่ยมสองรูปนั้นไม่คล้ายกัน ก็จะไม่สามารถใช้เงื่อนไขเกี่ยวกับอัตราส่วนของความยาวด้าน หรือเงื่อนไขเกี่ยวกับมุมคู่ที่สมนัยกันได้เลย
ตัวอย่างที่ 5 จงหาค่าของ x และ y
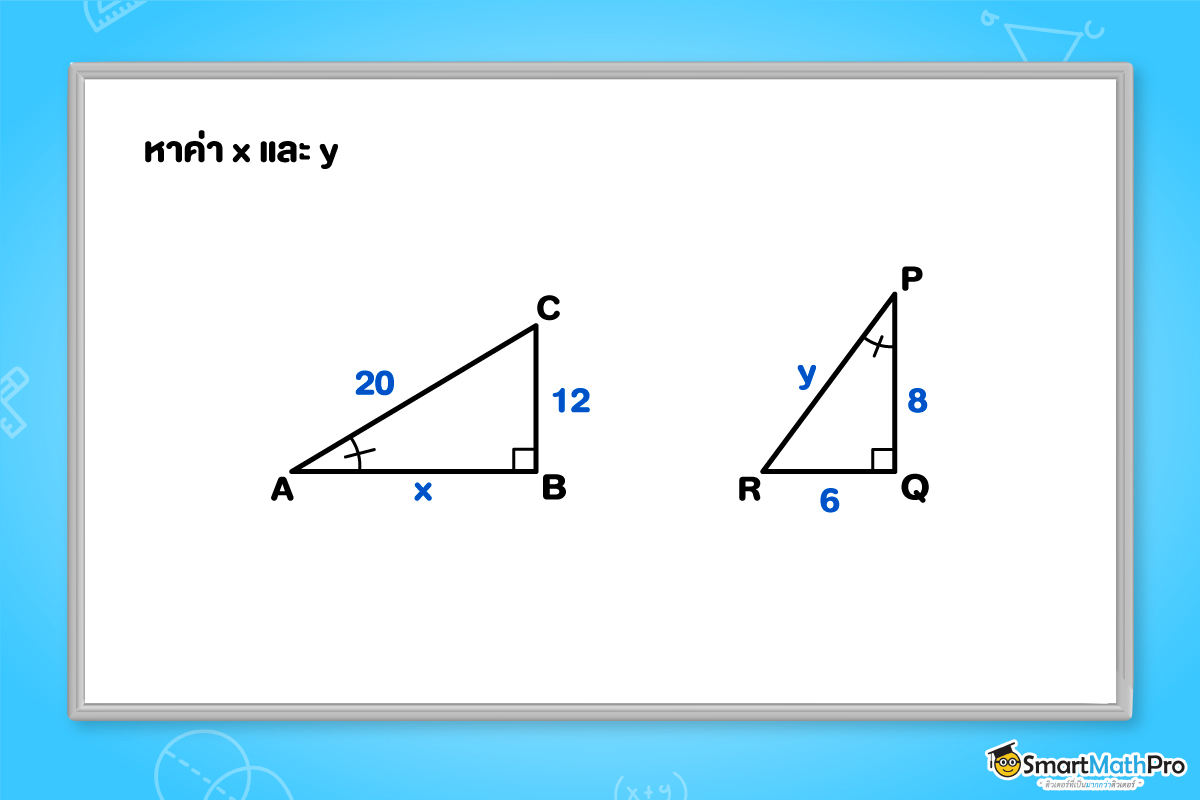
วิธีทำ
ขั้นตอนที่ 1 จะแสดงว่า \Delta ABC\sim\Delta PQR
จากรูป จะได้ว่า \hat{A}=\hat{P} และ \hat{B}=\hat{Q}=90^{\circ}
พิจารณา \hat{C}=180^{\circ}-(\hat{B}+\hat{A})=180^{\circ}-(90^{\circ}+\hat{A})=90^{\circ}-\hat{A}
\hat{R}=180^{\circ}-(\hat{Q}+\hat{P})=180^{\circ}-(90^{\circ}+\hat{A})=90^{\circ}-\hat{A}
จะได้ว่า \hat{C}=\hat{R}
ดังนั้น \Delta ABC\sim\Delta PQR
ขั้นตอนที่ 2 หาค่าของ x และ y
จะได้ว่า \frac{AB}{PQ}=\frac{BC}{QR}
\frac{x}{8}=\frac{12}{6}
x=(\frac{12}{6})(8)=16
จะได้ว่า \frac{PR}{AC}=\frac{QR}{BC}
\frac{y}{20}=\frac{6}{12}
x=(\frac{6}{12})(20)=10
ดังนั้น x=16 และ y=10
ข้อสังเกต จากตัวอย่างที่ 5 เมื่อรูปสามเหลี่ยมสองรูปใด ๆ มีมุมที่มีขนาดเท่ากันสองคู่ มุมที่เหลืออยู่จะกางเท่ากันเสมอ
ดังนั้นเมื่อน้องทำโจทย์ในบทนี้ เมื่อน้อง ๆ เจอรูปสามเหลี่ยมที่มีมุมขนาดเท่ากันเป็นคู่ ๆ เพียงสองคู่ ก็สามารถสรุปได้เลยว่ารูปสามเหลี่ยมสองรูปนั้นคล้ายกันนะ
โจทย์ปัญหาเกี่ยวกับรูปสามเหลี่ยม
น้อง ๆ อาจสังเกตว่าในแทบจะทุกบทของเนื้อหาคณิตม.ต้นจะต้องปิดท้ายด้วยหัวข้อโจทย์ปัญหาเสมอเลยใช่ไหม ในบทนี้ก็เช่นกันนะ เราสามารถนำความรู้เรื่องรูปสามเหลี่ยมคล้ายกันไปใช้ในการแก้ปัญหาในชีวิตประจำวันได้นะ พี่แนะนำว่าให้น้อง ๆ ลองถอดข้อความที่โจทย์กำหนดให้มาเป็นแผนภาพก่อน แล้วหารูปสามเหลี่ยมที่คล้ายกันให้เจอ ก็จะโจทย์ปัญหาได้แล้วนะ สังเกตได้จากตัวอย่างต่อไปนี้เลย
ตัวอย่างที่ 6
จุ๋มไปเที่ยวสวนสัตว์แห่งหนึ่งและได้พกเอาตลับเมตรไปด้วย จุ๋มต้องการวัดส่วนสูงของยีราฟด้วยการใช้เงา โดยจุ๋มยืนอยู่ตรงเงาของปลายหัวของยีราฟพอดี จุ๋มวัดเงาของยีราฟได้ยาว 8 เมตร จุ๋มวัดเงาของตัวเองได้ยาว 3.4 เมตร ถ้าจุ๋มสูง 170 เซนติเมตร แล้วยีราฟจะสูงเท่าใด
วิธีทำ
กำหนดให้ยีราฟสูงเท่ากับ CB = x เมตร
AB แทนความยาวของเงาของยีราฟ คือ 8 เมตร
DE แทนความสูงของจุ๋ม คือ 1.7 เมตร
AE แทนความยาวของเงาของจุ๋ม คือ 3.4 เมตร
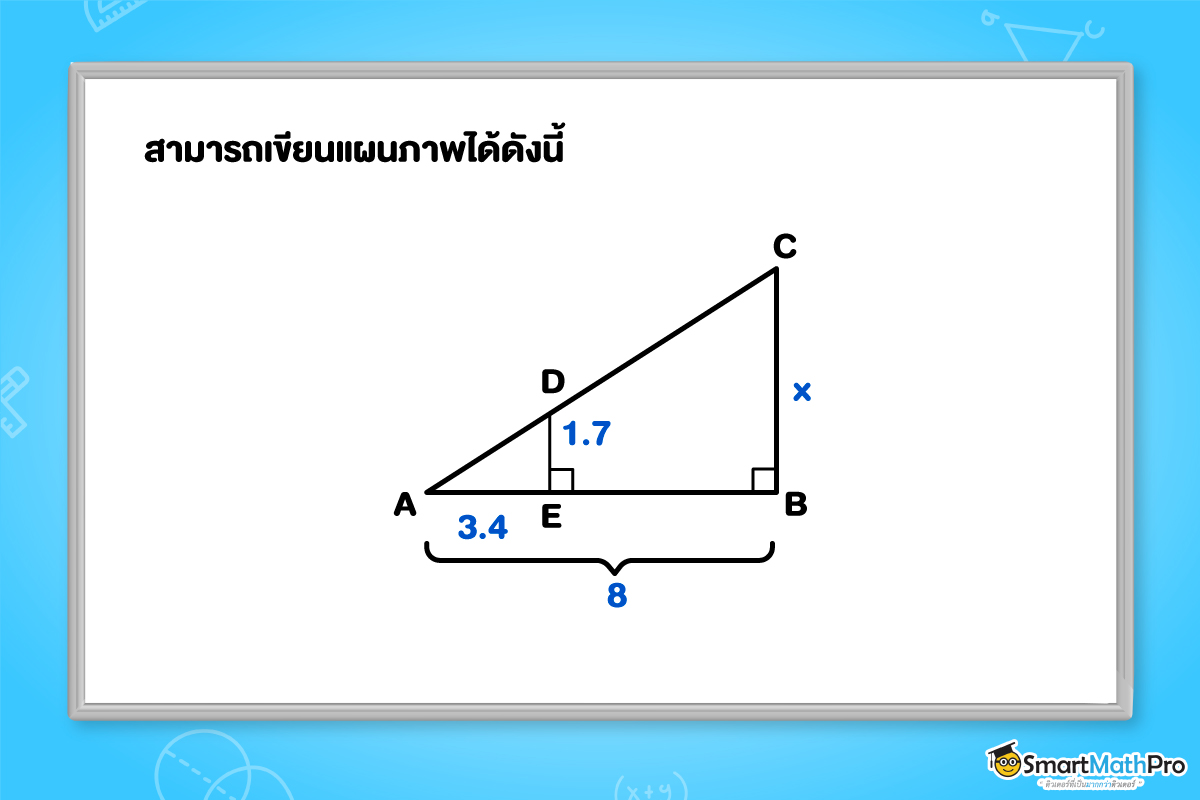
พิจารณา \Delta ABC และ \Delta AED
จะได้ว่า \hat{A}=\hat{A} เนื่องจากเป็นมุมร่วมและ \hat{B}=\hat{E} = 90 ^{\circ}
จากข้อสังเกต จะได้ว่า \hat{C}=\hat{D}
ดังนั้น \Delta ABC \sim\Delta AED จะได้ว่า \frac{AB}{AE}=\frac{BC}{ED}
\frac{8}{3.4}=\frac{x}{1.7}
x=(\frac{8}{3.4}) (1.7)=4
ดังนั้น ยีราฟสูง 4 เมตร
จะเห็นได้ว่า ความคล้ายในคณิตศาสตร์ ไม่ใช่การมองด้วยสายตาแล้วบอกได้เลยว่า สิ่งหนึ่งคล้ายสิ่งหนึ่ง แต่จะต้องมีการพิสูจน์ว่ารูปเรขาคณิตที่เห็นนั้นคล้ายกันจริง ๆ หรือไม่ อ่านมาถึงตรงนี้คงมีหลายคนเริ่มกังวลว่าคณิต ม.3 จะยากเกินไปมั้ย T_T พี่ไม่อยากให้ทุกคนท้อหรือคิดว่ามันเป็นเรื่องยากถึงขนาดที่ว่าเราจะทำไม่ได้น้าาาา ลองทบทวนจุดที่ไม่เข้าใจก่อน หรือจะฝึกทำโจทย์เยอะ ๆ ก็ได้ ซึ่งพี่ได้นำโจทย์มาให้น้อง ๆ ดาวน์โหลดไปฝึกทำกันได้ฟรี ๆ เลยน้า สามารถดาวน์โหลดแบบฝึกหัดความคล้าย ม.3 มาฝึกทำเพื่อเตรียมตัวล่วงหน้า หรือถ้าใครเรียนผ่านไปแล้วก็สามารถกลับมาฝึกทำโจทย์เพื่อเสริมพื้นฐานคณิต ม.ต้น ให้แข็งแรงได้น้าาา
เนื้อหาคณิต ม.3 ถือว่าเป็นอะไรที่สำคัญมากเพราะนอกจากจะเป็นเนื้อหาที่ยากที่สุดในคณิต ม.ต้น แล้วยังเป็นส่วนสำคัญที่อาจจะใช้ในการสอบเข้า ม.4 ด้วย สำหรับใครที่ลองทำโจทย์แล้ว แต่ยังมีเนื้อหาบางจุดที่ไม่เข้าใจ พี่ขอแนะนำคอร์สติวคณิต ม.3 จาก SmartMathPro เล้ยยย มีสอนทั้งเทอม 1 และเทอม 2 ปูพื้นฐานให้แบบละเอียดพร้อมพาทำโจทย์จนน้องสามารถทำเองได้ ใครสนใจดูรายละเอียดเพิ่มเติม คลิก ได้เลย
ดูคลิปติว ความคล้าย ม.3
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง Youtube Channel : SmartMathPro
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุป แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 พร้อมโจทย์+เฉลย
สรุป อสมการเชิงเส้นตัวแปรเดียว ม.3 พร้อมแจกโจทย์และเฉลย
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สถิติ ม.3 สรุปเนื้อหาคณิตม.ต้นหลักสูตรใหม่ พร้อมแจกโจทย์ให้ลองทำ !
สรุป พาราโบลา (ฟังก์ชันกำลังสอง) ม.3 พร้อมแจกสูตรและโจทย์ฟรี
สรุป วงกลม ม.3 ทฤษฎีบทวงกลม พร้อมแจกแบบฝึกหัดฟรี !
ตรีโกณมิติ ม.3 สรุปเนื้อหาพร้อมโจทย์แบบจัดเต็ม จบในที่เดียว !
คณิตศาสตร์ ม.3 เทอม 1, เทอม 2 เรียนอะไรบ้าง ? อัปเดตตาม สสวท.
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
