SMP_Toeyคณิต ม.ต้น
สรุปเนื้อตรีโกณมิติ ม.3 พร้อมโจทย์และวิธีการทำ

ใครกำลังหาสรุปเนื้อหา ตรีโกณมิติ ม.3 อยู่ ต้องรีบมารวมกันตรงนี้เลยยย วันนี้พี่เตรียมเนื้อหานี้มาให้น้อง ๆ ม.3
และน้อง ๆ ม.2 ที่อยากเตรียมตัวล่วงหน้าโดยเฉพาะเลยย เพราะพี่เชื่อว่าตรีโกณเป็นอีก 1 วิชาที่ยากและต้องเป็นไม้เบื่อ
ไม้เมาของหลายคนแน่นอนนน แต่ไม่ต้องกังวลไปน้าา เพราะพี่สรุปหัวข้อ สูตร พร้อมตัวอย่างโจทย์ตรีโกณมิติมาให้
หมดแล้ว ถ้าใครพร้อมแล้วเราก็ไปลุยกันเลย !

ตรีโกณมิติ ม.3

สรุปเนื้อหาตรีโกณม.3

ความหมายของอัตราส่วนตรีโกณมิติ

น้อง ๆ หลายคนเคยสงสัยไหมว่า เวลาที่เราเล่มเกม ไม่ว่าจะเป็นเกมขับรถ เกมเดินตะลุยสิ่งกีดขวาง คนพัฒนาเกมสร้างให้
ตัวละครเคลื่อนไหวได้ยังไง 

พี่ขอยกตัวอย่างเพิ่มเติม เช่น หากคนพัฒนาเกมต้องการกำหนดให้ตัวละครกระโดด ให้น้อง ๆ สังเกตการกระโดดแล้วจะเห็นว่าตัวละครจะพุ่งขึ้นไปจนถึงจุดสูงสุดและลงมายังจุดต่ำสุด (ซึ่งก็แล้วแต่เกมอีกเช่นกัน บางเกมอาจจะร่วงตกลงมาเลย บางเกมอาจจะพุ่งไปด้านหน้าอีกนิดนึง) นั่นแปลว่าเราจะต้องพิจารณา จุดเริ่มกระโดด จุดสูงสุด และ
จุดตกลงมา จากสามจุดนี้จะทำให้เห็นว่ามันคือรูปเรขาคณิต (ที่น้อง ๆ ทุกคนรู้จัก) นั่นคือรูปสามเหลี่ยมนั่นเอง

ถ้าเราต้องการคาดคะเนระยะการกระโดดต่าง ๆ เพิ่มเติม เราต้องใช้ความรู้เกี่ยวกับอัตราส่วนตรีโกณมิติมาช่วยใน
การคำนวณ

หากลองย้อนกลับไปในสมัยก่อน คนสนใจที่จะวัดความยาวของรูปสามเหลี่ยมชนิดต่าง ๆ จึงตั้งชื่อเล่นให้กับการวัด
ในลักษณะนี้ โดยกำหนดให้ชื่อนั้นมีที่มาจากคำว่า trigonon ที่แปลว่ารูปสามเหลี่ยม และ metron ที่แปลว่าการวัด รวมกันเป็นชื่อว่า trigonometry หรือ ตรีโกณมิติ นั่นเอง วันเวลาผ่านไปความรู้เรื่องตรีโกณมิติถูกใช้อย่างแพร่หลายและเป็นที่ต้องการอย่างมาก จนกลายที่ต้องเรียนในวิชาคณิตศาสตร์ไปแล้ววว

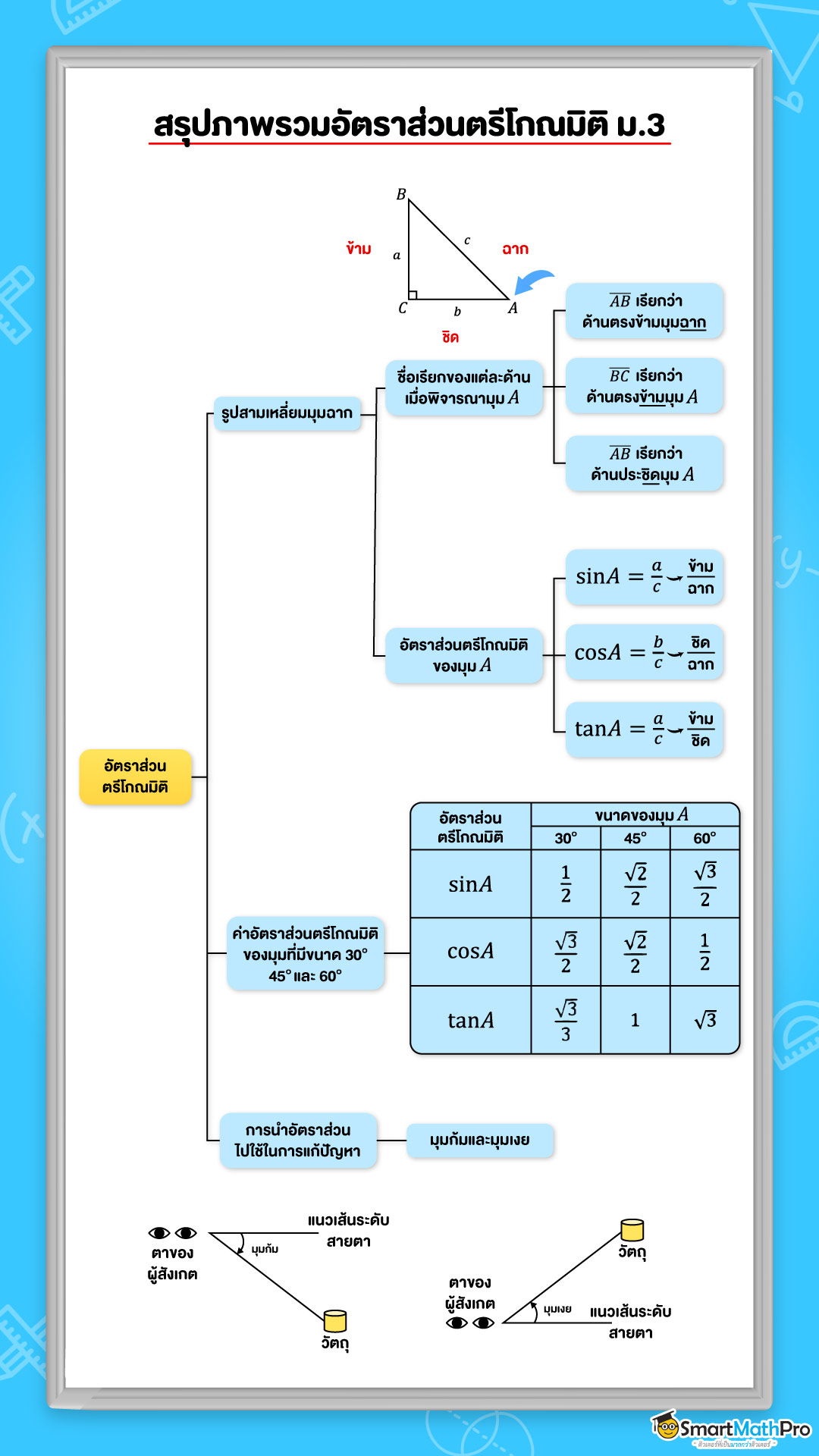
รูปสามเหลี่ยมมุมฉาก

จากที่เราได้รู้ความหมายไปแล้ว เราก็พอจะรู้แล้วว่าในบทนี้ เราจะสนใจรูปสามเหลี่ยมเป็นหลัก โดยรูปที่เราสนใจศึกษามากที่สุดในบทนี้ คือ รูปสามเหลี่ยมมุมฉากนั่นเอง เดี๋ยวเราลองมาดูกันเลยยย

รูปสามเหลี่ยมมุมฉาก คือ รูปสามเหลี่ยมที่มีมุมทั้งหมด 3 มุมแต่มี 1 มุมเป็นมุมฉาก ถ้าเราให้รูปสามเหลี่ยมมุมฉาก ABC ที่มี C เป็นมุมฉาก เราจะเรียกแต่ละด้านดังต่อไปนี้

รูปสามเหลี่ยมมุมฉากและด้านที่เกี่ยวข้องกับมุม A ในตรีโกณมิติ ม.3

\overline{AB} คือ ด้านตรงข้ามมุมฉาก (hypotenuse)

\overline{BC} คือ ด้านตรงข้ามมุม A (the opposite side of angle A)

\overline{AC} คือ ด้านประชิดมุม A (the adjacent side of angle A)

ข้อสังเกต ชื่อด้านที่เราเรียกตามรูปข้างต้นจะพิจารณาที่มุม A เป็นหลัก แต่ถ้าเปลี่ยนมาพิจารณามุม B เราก็ยังมีชื่อเรียกของด้านเหล่านี้เหมือนกัน โดย \overline{AC} จะเป็นด้านตรงข้ามมุม B และ \overline{BC} จะเป็นด้านประชิดมุม B นั่นเอง

หลังจากที่น้องได้รู้จักชื่อเรียกด้านต่าง ๆ ของสามเหลี่ยมมุมฉากเพื่อให้จดจำและเข้าใจง่ายแล้ว ทีนี้เราจะมาเรียนรู้ว่า
จะเอามันมาใช้ประโยชน์ยังไงกัน !! ซึ่งจะเอามาใช้ในเรื่องอัตราส่วนตรีโกณมิติเนี่ยแหละ ไปต่อกันเลยยย

อัตราส่วนตรีโกณมิติ

รูปสามเหลี่ยมมีองค์ประกอบที่สำคัญ คือ ด้านแต่ละด้านของรูปสามเหลี่ยมและมุมทั้ง 3 มุม ซึ่งต่อไปเราจะมาดู
ความสัมพันธ์ของแต่ละองค์ประกอบกันเลย

รูปสามเหลี่ยมมุมฉาก ABC ซึ่งมี C เป็นมุมฉาก เมื่อเราพิจารณามุมมุมหนึ่งที่ไม่ใช่มุมฉาก เช่น มุม A แล้วจะได้ว่า

บทนิยามรูปสามเหลี่ยมมุมฉากในตรีโกณ ม.3

ไซน์ของมุม A, โคไซน์ของมุม A และแทนเจนต์ของมุม A เนี่ยแหละ เราจะเห็นว่ามันคือการเอาความยาวด้านแต่ละด้านมาเทียบกันเป็นคู่ ๆ เราเรียกมันว่าอัตราส่วนตรีโกณมิติ ซึ่งอัตราส่วนตรีโกณมิติเดียวกันของมุมมุมหนึ่งเป็นค่าคงตัวค่าหนึ่งเสมอ และเราจะนิยมเขียน   

sinA แทน ไซน์ของมุม A และอ่านว่า ไซน์ A

cosA แทน โคไซน์ของมุม A และอ่านว่า คอส A

tanA แทน แทนเจนต์ของมุม A และอ่านว่า แทน A

ตัวอย่างที่ 1 จากรูปสามเหลี่ยมมุมฉากที่กำหนดให้ จงหาค่า sinA, cosA, tanA, sinB, cosB, tanB

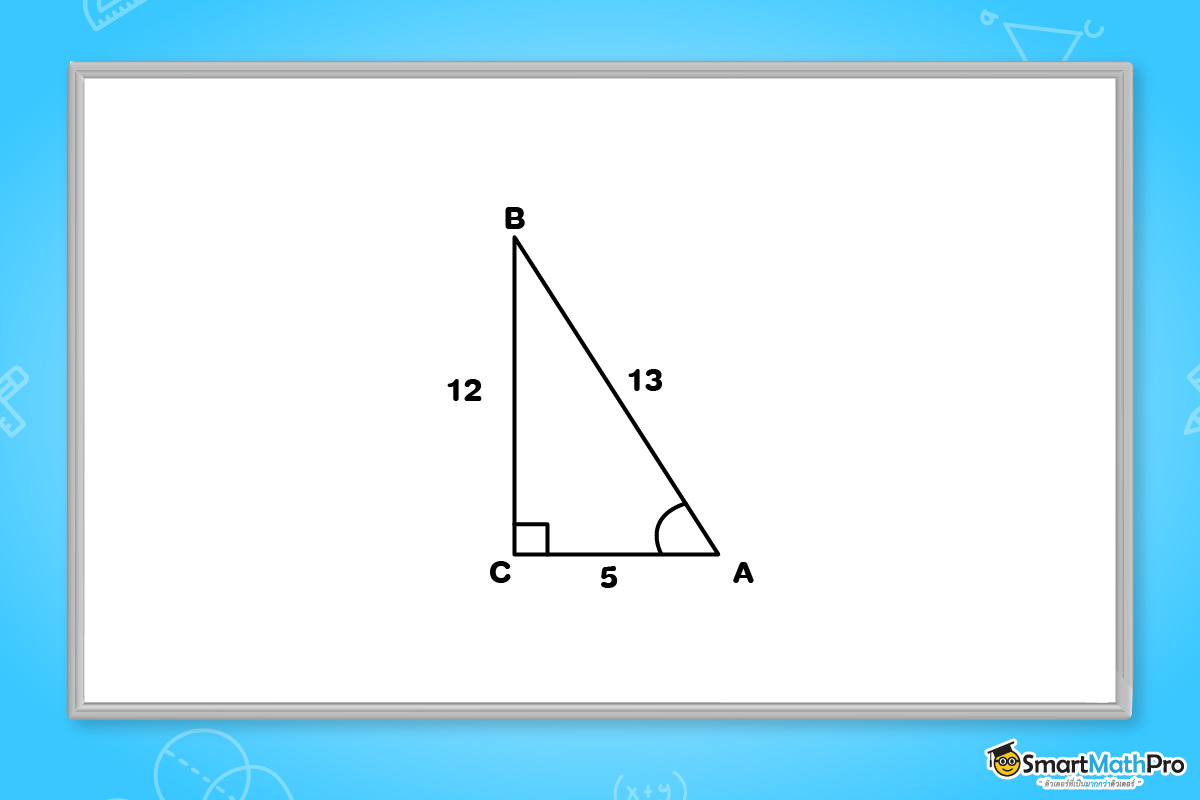
แบบฝึกหัดรูปสามเหลี่ยมมุมฉากเรื่องตรีโกณ ม.3

จากรูปจะได้ว่า

sinA = \frac{12}{13}  

cosA = \frac{5}{13} 

tanA = \frac{12}{5} 

sinB = \frac{5}{13} 

cosB = \frac{12}{13} 

tanB = \frac{5}{12}

อัตราส่วนตรีโกณมิติของมุมที่มีขนาด 30 องศา, 45 องศา และ 60 องศา

จากหัวข้อก่อนหน้าเราได้รู้จักกับอัตราส่วนตรีโกณมิติไปแล้ว ซึ่งเรารู้ว่าอัตราส่วนตรีโกณมิติในมุมที่มีขนาดเท่ากัน
จะมีค่าเท่ากัน ซึ่งจริง ๆ แล้วขนาดของมุมในรูปสามเหลี่ยมมุมฉากนั้นมีหลายมุมมากเลยนะ แต่ในระดับชั้น ม.3 เราจะโฟกัสแค่มุมแหลมที่มีขนาด 30^{\circ} , 45^{\circ} , 60^{\circ}

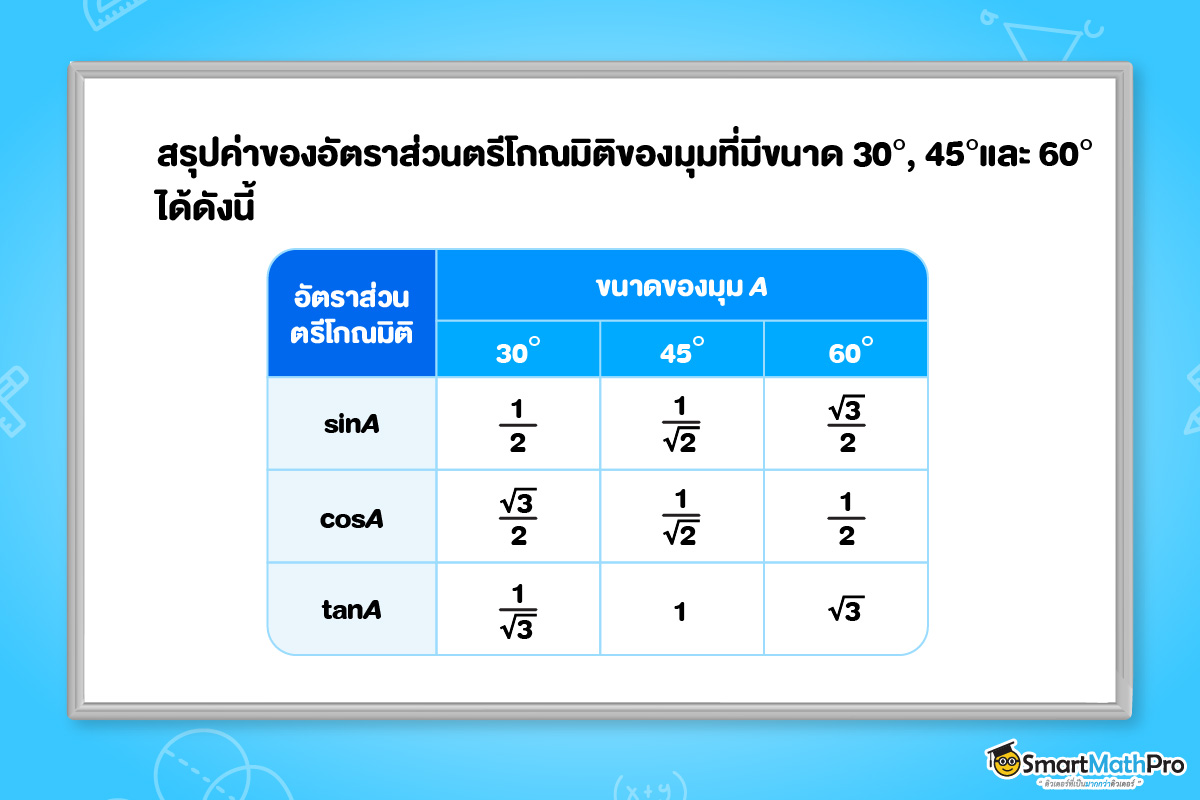
สรุปค่าของอัตราส่วนตรีโกณมิติ ม.3 ของมุมที่มีขนาด 30 , 45 และ 60 องศา

 สมบัติ
สำหรับรูปสามเหลี่ยมมุมฉากใด ๆ อัตราส่วนตรีโกณมิติเดียวกันของมุมที่มีขนาดเท่ากัน จะมีค่าเท่ากัน

ถ้าน้อง ๆ ยังจำค่าของอัตราส่วนตรีโกณมิติต่าง ๆ ของมุม 30^{\circ}, 45^{\circ}, 60^{\circ} จากในตารางไม่ได้ พี่มีเทคนิควิธีจำค่าของอัตราส่วนตรีโกณมิติแบบเก๋ ๆ ของมุม 30^{\circ}, 45^{\circ}, 60^{\circ} มาฝากกัน ยกมือซ้ายขึ้นมา แล้วลองไปดูกันว่าเทคนิคนี้มีวิธียังไงกันบ้างงง

วิธีใช้เทคนิคมือ (ซ้าย)

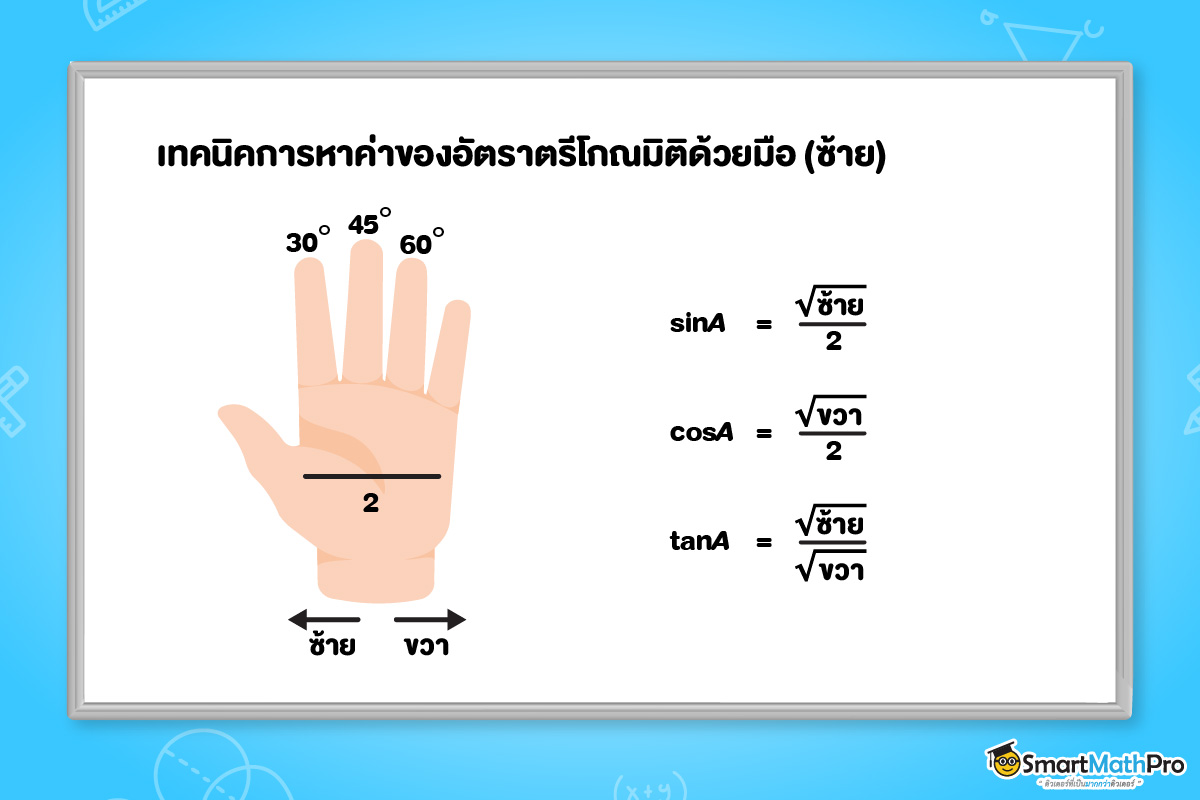
เทคนิคการหาค่าตรีโกณมิติด้วยมือซ้าย

ขั้นตอนการหาค่าโดยใช้เทคนิคมือ (ซ้าย) 

  • เลือกมุมที่เราต้องการพิจารณา
  • พับนิ้วลง ตามมุมในรูป เช่น ต้องการพิจารณามุม  30^{\circ} ให้พับนิ้วชี้ลง
  • การหาค่าของอัตราส่วนตรีโกณมิติ จะหาได้จากการนับจำนวนนิ้วจากด้านซ้ายหรือด้านขวาที่แตกต่างกัน

ลองใช้เทคนิคมือซ้ายในการหาค่า เช่น

  • ต้องการหาค่า sin60^{\circ}
    ให้พับนิ้วนางลง เหลือ 3 นิ้วทางด้านซ้าย เลยได้ว่าค่าของ sin60^{\circ} มีค่าเท่ากับ \frac{\sqrt{3}}{2} 
  • ต้องการหาค่า cos45^{\circ} 
    ให้พับนิ้วกลางลง เหลือ 2 นิ้วทางด้านขวา เลยได้ว่าค่าของ cos45^{\circ}  มีค่าเท่ากับ \frac{\sqrt{2}}{2} นั่นคือ cos45^{\circ}=\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\frac{1}{\sqrt{2}} จะเห็นว่าได้ค่าเท่ากับตารางด้านบนเลย
  • ต้องการหาค่า tan60^{\circ}
    ให้พับนิ้วนางลง มี 3 นิ้วทางด้านซ้าย และ 1 นิ้วทางด้านขวา เลยได้ว่าค่าของ tan60^{\circ}
    มีค่าเท่ากับ \frac{\sqrt{3}}{\sqrt{1}}=\sqrt{3}

ตัวอย่างที่ 2 จากรูปสามเหลี่ยมต่อไปนี้ จงหาขนาดของมุม x และมุม y 

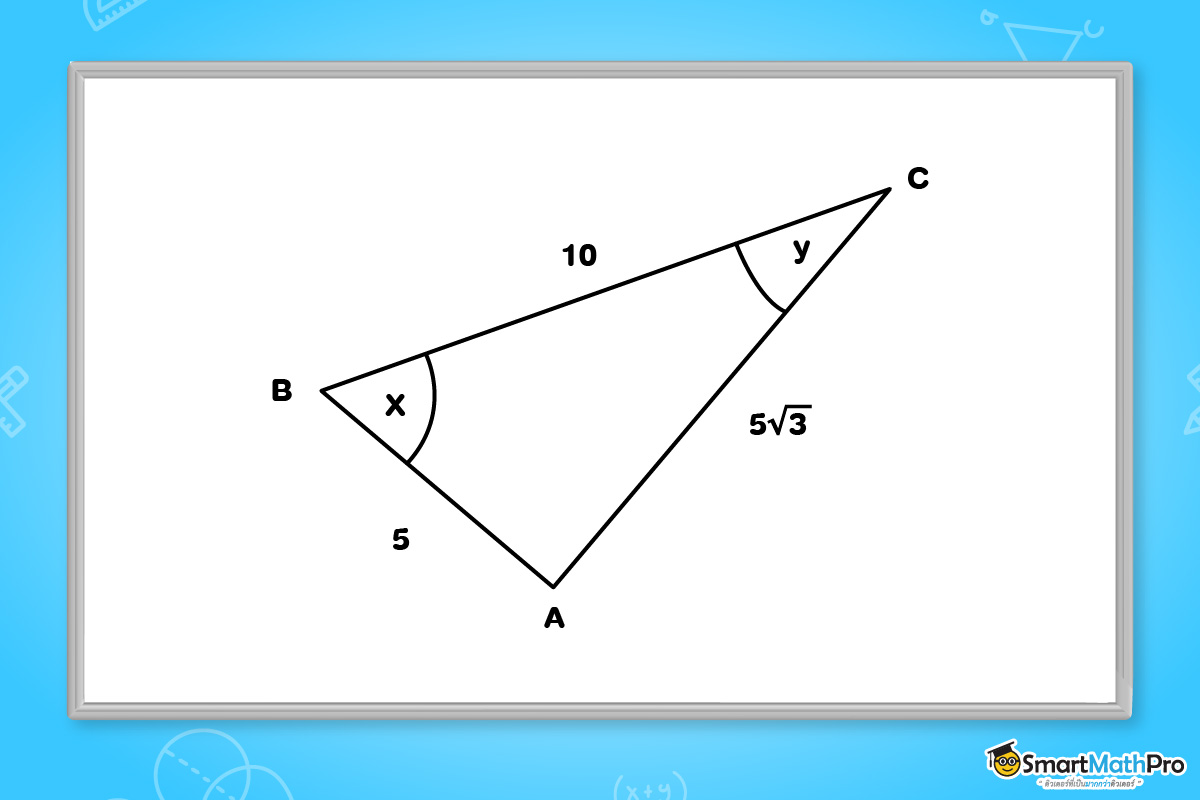
โจทย์การฝึกใช้เทคนิคมือซ้ายสำหรับหาค่าตรีโกณมิติ

แนวคิด เราจะมาพิจารณากันว่ารูปสามเหลี่ยมข้างต้นนี้ เป็นรูปสามเหลี่ยมมุมฉากหรือไม่ ถ้าเป็นรูปสามเหลี่ยมมุมฉากจะใช้อัตราส่วนตรีโกณมิติในการหาขนาดของมุมต่อไป

วิธีทำ

จากทฤษฎีบทพีทาโกรัส “กำลังสองของความยาวของด้านตรงข้ามมุมฉากเท่ากับผลบวกของกำลังสองของความยาวของด้านประกอบมุมฉาก”

จากรูปสามเหลี่ยม

ABC จะได้ว่า CB^{2}=AB^{2}+AC^{2}

แทนค่าได้ว่า 10^{2}=5^{2}+(5\sqrt{3})^{2}

100=25+75

100=100 ซึ่งเป็นจริง

ดังนั้น รูปสามเหลี่ยม ABC เป็นรูปสามเหลี่ยมมุมฉาก ที่มีมุม A เป็นมุมฉาก

จากมุม x

พิจารณา cosx =\frac{5}{10}=\frac{1}{2}

จาก cos60^{\circ}=\frac{1}{2}

ดังนั้น x=60^{\circ}

จากมุม y

พิจารณา tany=\frac{5}{5\sqrt{3}}=\frac{1}{\sqrt{3}}

จาก tan30^{\circ}=\frac{1}{\sqrt{3}}

ดังนั้น y=30^{\circ}

ตัวอย่างที่ 3 จากรูปสามเหลี่ยมมุมฉากต่อไปนี้ จงหาค่า x และ y

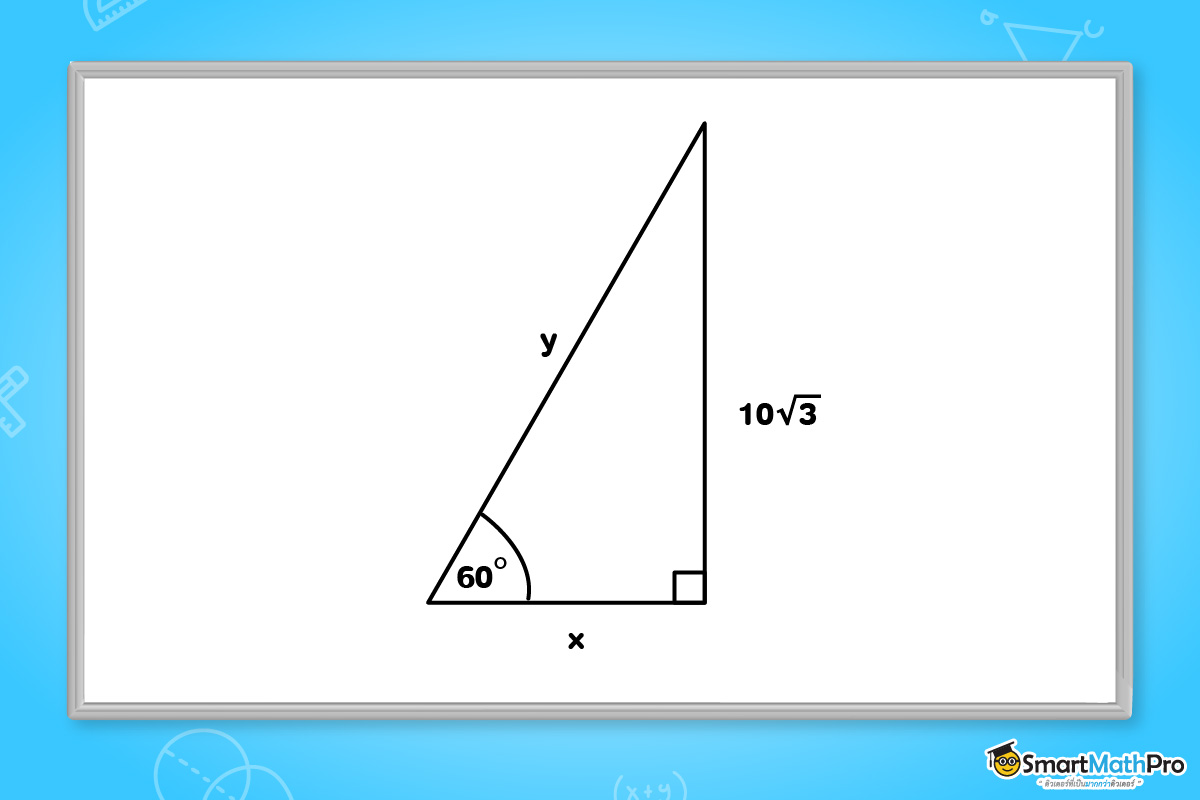
แบบฝึกหัดรูปสามเหลี่ยมมุมฉากเรื่องตรีโกณมิติ ม.3

วิธีทำ จาก tan60^{\circ}=\sqrt{3} 

จากรูป จะได้ว่า \frac{10\sqrt{3}}{x}=\sqrt{3} 

 10\sqrt{3}=x\sqrt{3}  

x=10 

จากค่า sin60^{\circ}=\frac{\sqrt{3}}{2} 

จากรูปจะได้ว่า \frac{10\sqrt{3}}{y} =\frac{\sqrt{3}}{2} 

(10\sqrt{3})(2)=y\sqrt{3}  

 20\sqrt{3}=y\sqrt{3}  

y=20

ตัวอย่างที่ 4 จงหาผลลัพธ์ของ sin30^{\circ} + (cos45^{\circ})^{2}

วิธีทำ

จาก sin30^{\circ}=\frac{1}{2},cos45^{\circ}=\frac{\sqrt{2}}{2}

จะได้ว่า sin30^{\circ} + (cos45^{\circ})^{2} = \frac{1}{2}+\left (\frac{\sqrt{2}}{2}\right)^{2}=\frac{1}{2}+\frac{2}{4}=\frac{1}{2}+\frac{1}{2}=1

ดังนั้น sin30^{\circ} + (cos45^{\circ})^{2}  =1

โจทย์ปัญหาอัตราส่วนตรีโกณมิติ

ในการแก้ปัญหาที่ต้องใช้อัตราส่วนตรีโกณมิติ จำเป็นต้องทราบขนาดของมุมด้วยน้า และการแก้โจทย์ปัญหาในเรื่องนี้เราจะใช้มุมที่เกิดจากการมองด้วยสายตา ซึ่งมีคำที่ใช้ในการเรียกมุมที่ทำกับแนวเส้นระดับสายตา 2 แบบด้วยกัน คือ
มุมก้ม (angle of depression) และมุมเงย (angle of elevation)

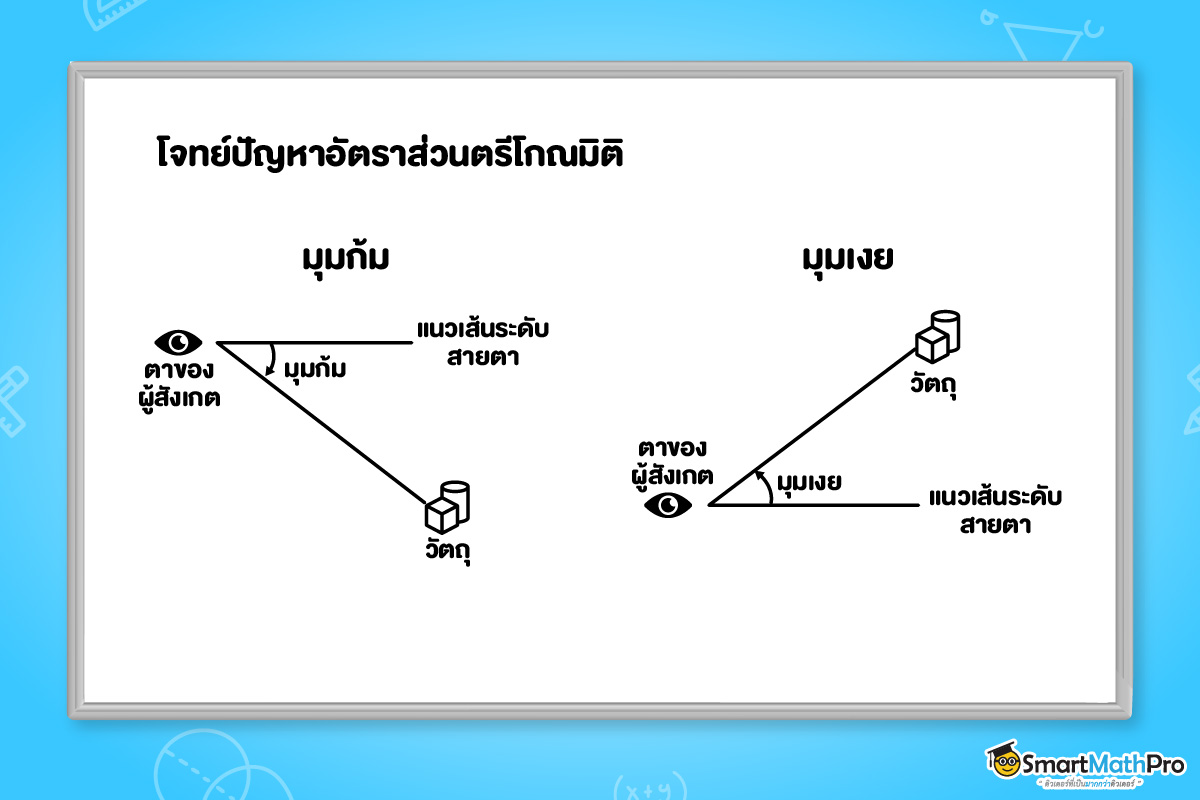
เทคนิคมุมก้มและมุมเงยสำหรับทำโจทย์ตรีโกณมิติ

จากรูป จะเห็นได้ว่า

  • มุมก้ม เป็นมุมที่เกิดจากการมองวัตถุที่อยู่ต่ำกว่าแนวเส้นระดับสายตา
  • มุมเงย เป็นมุมที่เกิดจากการมองวัตถุที่อยู่สูงกว่าแนวเส้นระดับสายตา

เรามาดูตัวอย่างวิธีการใช้งาน โดยผ่านตัวอย่างนี้กัน

ตัวอย่างที่ 5 บันไดวางพาดกำแพงโดยทำมุม 30^{\circ} กับพื้น ถ้าปลายอีกด้านของบันไดอยู่ห่างจากฐานกำแพงอยู่
6\sqrt{3} เมตร แล้วบันไดยาวกี่เมตร

วิธีทำ

โจทย์ปัญหาอัตราส่วนตรีโกณ ม.3 เรื่องมุมก้มและมุมเงย

กำหนดให้ บันไดยาว x เมตร

จะได้ว่า cos30^{\circ}=\frac{6\sqrt{3}}{x} 

จาก cos30^{\circ}=\frac{\sqrt{3}}{2} 

จะได้ \frac{\sqrt{3}}{2}=\frac{6\sqrt{3}}{x}    

x\sqrt{3}=12\sqrt{3}   

x=12 

ดังนั้น บันไดยาว 12   เมตร

เป็นยังไงกันบ้างงง กับเนื้อหาตรีโกณมิติ ม.3 หลายคนพออ่านจบแล้ว อาจจะรู้สึกว่าเนื้อหาเยอะ แล้วก็ยากด้วย แต่ถ้าลองค่อย ๆ ทำความเข้าใจ รวมถึงทบทวนเนื้อหาและฝึกทำโจทย์บ่อย ๆ พี่เชื่อว่าเนื้อหาตรีโกณมิติ ม.3 ก็จะไม่ยากเกินความสามารถของทุกคนแน่นอนน ซึ่งถ้าใครอยากได้โจทย์เอาไว้ซ้อมมือ พี่ก็มีแบบฝึกหัดตรีโกณมิติ ม.3 มาให้ทุกคนได้ลองทำด้วยน้าา ไปดาวน์โหลดกันได้เลยย

แต่ถ้าใครที่ลองทบทวนหรือฝึกทำโจทย์เองแล้วยังมีเนื้อหาบางจุดที่ยังไม่เข้าใจ ต้องการคนช่วยไกด์เนื้อหาให้เข้าใจมากขึ้น พี่ขอแนะนำคอร์สติวคณิต ม.3 จาก SmartMathPro เลยย คอร์สนี้มีทั้งเนื้อหาของทั้งเทอม 1 และเทอม 2 ครบทุกบท ซึ่งพี่จะปูพื้นฐานให้แบบละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. พร้อมพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ แถมยังมี Quiz ทบทวนความเข้าใจแต่ละบทให้ด้วยน้า 

ดังนั้นน้อง ๆ คนไหนที่พื้นฐานไม่แน่นก็เรียนได้ ไม่ต้องกังวลเลยว่าจะเรียนไม่ทัน !! และถ้าโรงเรียนของน้อง ๆ สอนไม่ตรงตามคอร์สที่มี ก็สามารถเลือกเรียนแบบแยกบทได้เลยย เริ่มต้นเพียง 360 บาทเท่านั้น ใครสนใจดูรายละเอียดเพิ่มเติม คลิก ได้เลยน้าา

ดูคลิปติว ตรีโกณมิติ ม.3

ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro

บทความ แนะนำ

บทความ แนะนำ

สรุปเนื้อหาคณิตม.3 เรื่องการแยกตัวประกอบของพหุนามที่มีดีกรีสูงกว่าสอง
สรุป แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 พร้อมโจทย์+เฉลย
สรุปเนื้อหาคณิตม.3 อสมการเชิงเส้นตัวแปรเดียว
สรุป อสมการเชิงเส้นตัวแปรเดียว ม.3 พร้อมแจกโจทย์และเฉลย
สรุปเนื้อหาคณิตม.3 เรื่องสมการกำลังสองตัวแปรเดียว
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สรุปเนื้อหาคณิต ม.3 เรื่อง สถิติ (แผนภาพกล่อง)
สถิติ ม.3 (แผนภาพกล่อง) สรุปเนื้อหา พร้อมแจกโจทย์และเฉลยฟรี!
สรุปเนื้อหาคณิตศาสตร์ ม.3 เรื่อง พาราโบลา (กราฟฟังก์ชันกำลังสอง)
สรุป พาราโบลา (ฟังก์ชันกำลังสอง) ม.3 พร้อมแจกสูตรและโจทย์ฟรี
สรุปเนื้อหาคณิตม.3 เรื่องความคล้าย
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
สรุปเนื้อหาคณิตม.3 เรื่องวงกลม
สรุป วงกลม ม.3 ทฤษฎีบทวงกลม พร้อมแจกแบบฝึกหัดฟรี !

สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่

Line : @smartmathpronews 

FB : Pan SmartMathPro ติวคณิต By พี่ปั้น 

IG : pan_smartmathpro

X : @PanSmartMathPro 

Tiktok : @pan_smartmathpro

Post Views: 42,201
Share