พอได้ยินชื่อ “ฟังก์ชันกำลังสอง” ในเนื้อหาคณิตศาสตร์ ม.3 น้อง ๆ บางคนก็อาจจะรู้สึกว่าไม่เคยได้ยินชื่อนี้มาก่อน และคิดว่าต้องเป็นเนื้อหาที่ยากมากแน่ ๆ แต่ถ้าพี่พูดคำว่า “พาราโบลา” หลายคนก็อาจจะร้องอ๋อกันขึ้นมาบ้างแล้วใช่ไหม > <
แต่ถ้าใครยังไม่เคยได้ยินชื่อนี้มาก่อนก็ไม่เป็นไรน้าา วันนี้พี่จะพาทุกคนไปรู้จักกับฟังก์ชันกำลังสอง หรือ พาราโบลา ให้มากขึ้นในบทความนี้ตั้งแต่ความหมายของพาราโบลา สมการของพาราโบลา และความเชื่อมโยงระหว่างพาราโบลา ม.ต้น กับ ม.ปลาย แถมท้ายบทความมีแจกแบบฝึกหัดให้ฝึกซ้อมมือด้วยยย ไปอ่านกันเลยดีกว่าา
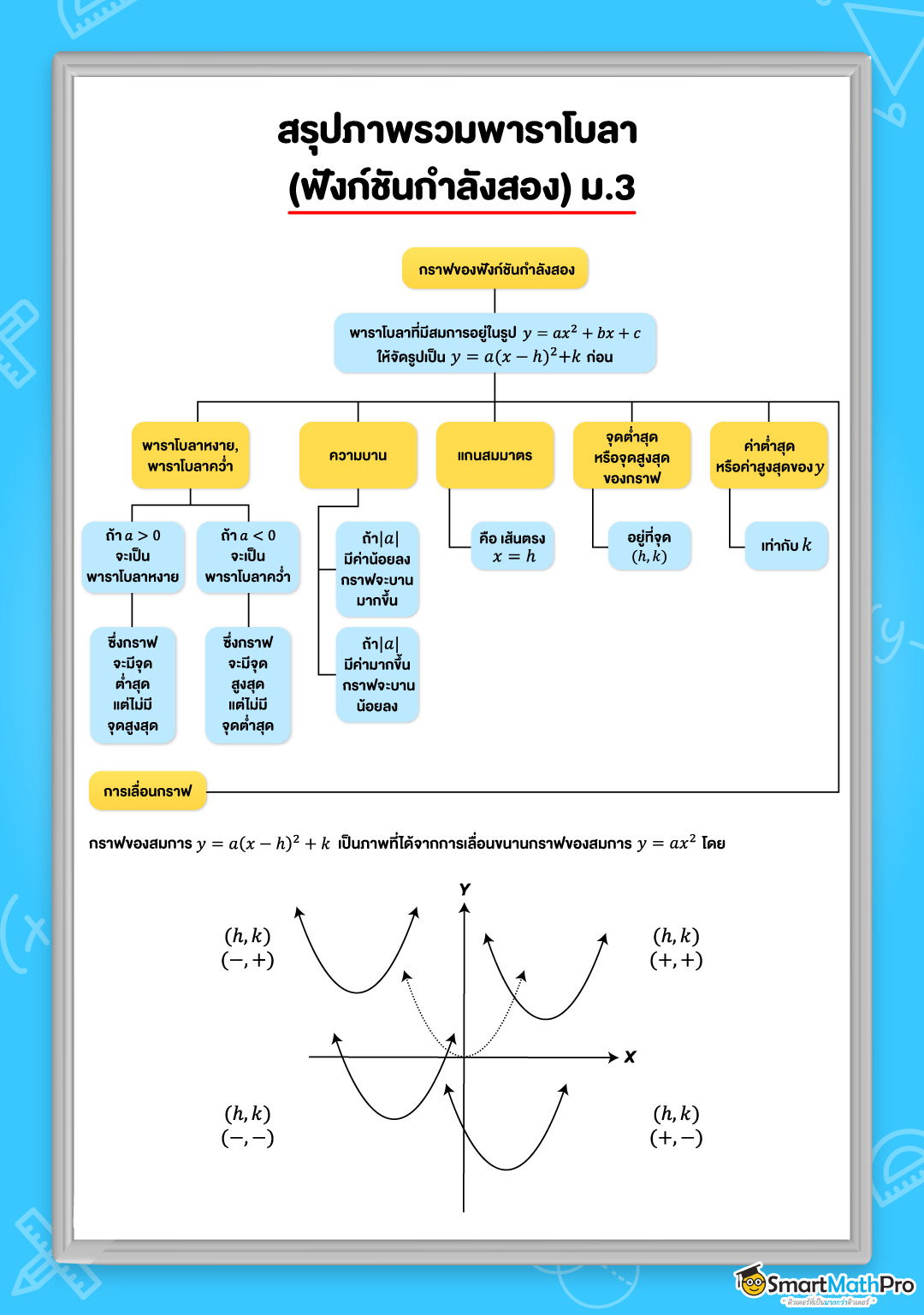
พาราโบลา (ฟังก์ชันกำลังสอง) คืออะไร ?
น้อง ๆ ลองสังเกตสิ่งที่อยู่รอบ ๆ ตัวจะพบสิ่งก่อสร้าง วัสดุ อุปกรณ์ หรือลักษณะในธรรมชาติบางอย่าง ที่ส่วนประกอบมีลักษณะเป็นเส้นโค้งทางเรขาคณิต ตัวอย่างสิ่งก่อสร้างระดับโลก เช่น บริเวณขาของหอไอเฟล (Eiffel Tower) ในประเทศฝรั่งเศส ที่มีความโค้ง หรือสะพานโกลเดนเกต (Golden Gate Bridge) ที่ซานฟรานซิสโก รัฐแคลิฟอร์เนีย สหรัฐอเมริกา ก็จะมีส่วนที่โค้ง ๆ โดยที่เส้นโค้งเหล่านี้จะมีลักษณะคล้ายกันเลย
กาลิเลโอ (Galileo Galilei) นักวิทยาศาสตร์ชาวอิตาลีที่มีชื่อเสียงของโลก พบว่าเมื่อเราโยนวัตถุ ไปในอากาศ เส้นทางการเคลื่อนที่ของวัตถุนั้นจะมีลักษณะเป็นเส้นโค้ง ในทางคณิตศาสตร์เรียกเส้นโค้งที่มีลักษณะดังกล่าวนี้ว่า พาราโบลา (parabola)
ซึ่งพี่จะพาทุกคนไปรู้จักกับสมการของฟังก์ชันกำลังสอง หรือที่เราเรียกกันว่า สมการของพาราโบลา ว่าจะมีรูปแบบหน้าตาของสมการเป็นแบบไหน ดูได้จากรูปด้านล่างนี้เลย !!
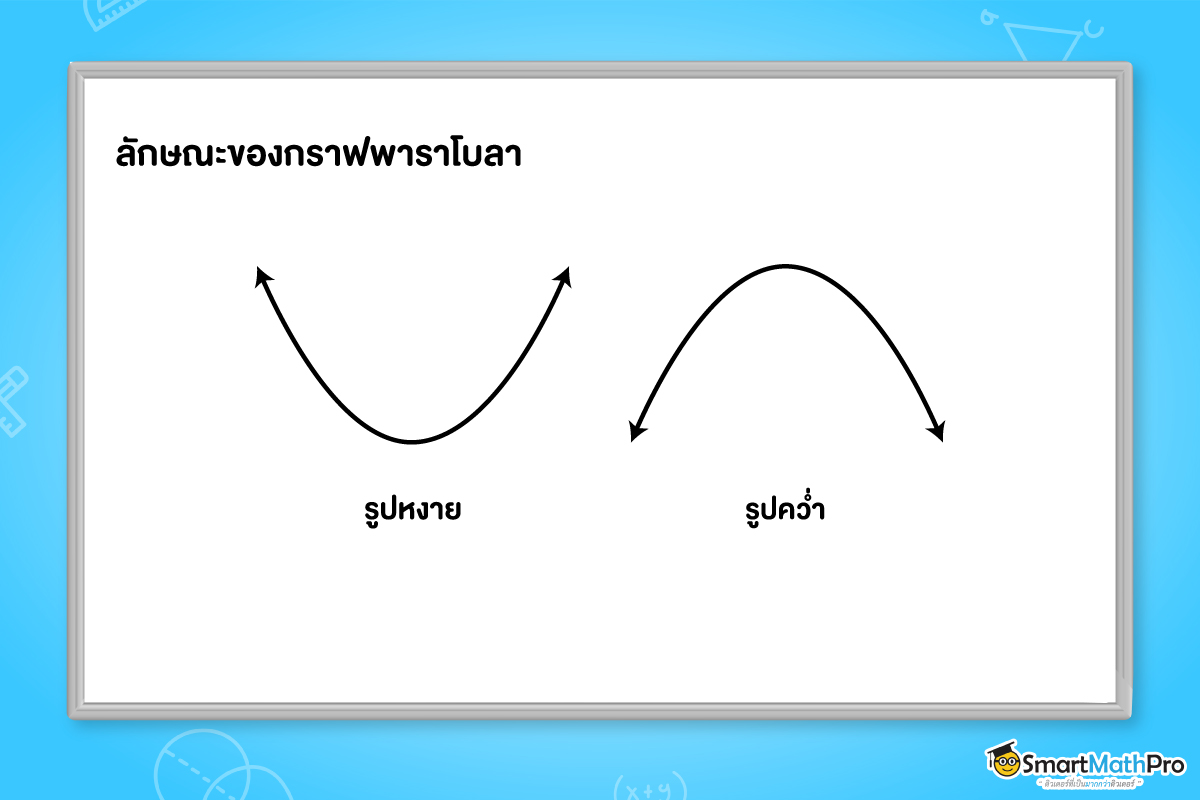
กราฟของพาราโบลาในระดับชั้นนี้ที่น้อง ๆ จะได้เรียนต่อไปจะมีลักษณะ 2 แบบ คือ กราฟเป็นพาราโบลาหงาย หรือเป็นพาราโบลาคว่ำ ตามรูปด้านล่างนี้ โดยสมการของฟังก์ชันกำลังสองที่อยู่ในรูป y=ax^2+bx+c จะเรียกว่า สมการของพาราโบลา
ตัวอย่างที่ 1
สมการในแต่ละข้อต่อไปนี้ เป็นสมการของพาราโบลาหรือไม่
1. y=x^2-x+2
ตอบ เป็นสมการของพาราโบลา
2. x=y^2+y
ตอบ ไม่เป็นสมการของพาราโบลา
3. y=\frac{1}{x^2}
ตอบ ไม่เป็นสมการของพาราโบลา
4. x^2+y=9
ตอบ เป็นสมการของพาราโบลา
5. y= (x+2)(x-1)
ตอบ เป็นสมการของพาราโบลา
จากตัวอย่างข้างต้น วิธีแยกว่าสมการใดเป็นหรือไม่เป็นสมการของพาราโบลาทำได้ง่ายมากเลยน้าา คือ ให้น้อง ๆ ลองจัดรูปสมการที่โจทย์กำหนดให้อยู่ในรูป y=ax^2+bx+c ว่าสามารถทำได้หรือเปล่า (ซึ่งอาจทำได้โดยการย้ายข้างของสมการเพื่อแยกตัวแปร y ให้อยู่เพียงตัวเดียว รวมถึงการกระจายผลคูณในวงเล็บออกมาเหมือนข้อย่อยที่ 5) หรือจัดรูปด้วยวิธีอื่น ๆ)
ถ้าสมการนั้นสามารถจัดรูปได้ เราจะได้ว่าสมการนั้นเป็นสมการของพาราโบลา แต่ถ้าพยายามจัดรูปจนถึงที่สุดแล้วก็ยังไม่สามารถจัดให้อยู่ในรูป y=ax^2+bx+c ได้ เหมือนในข้อย่อยที่ 2) และ 3) ก็จะได้ว่าสมการนั้นไม่เป็นสมการของพาราโบลานั่นเองง
หลังจากเราได้รู้จักสมการและลักษณะคร่าว ๆ ของกราฟของพาราโบลาแล้ว เรามาทำความรู้จักกับส่วนประกอบต่าง ๆ ของกราฟพาราโบลาเพิ่มเติมกันดีกว่า ซึ่งส่วนประกอบก็มีตามนี้เลยย
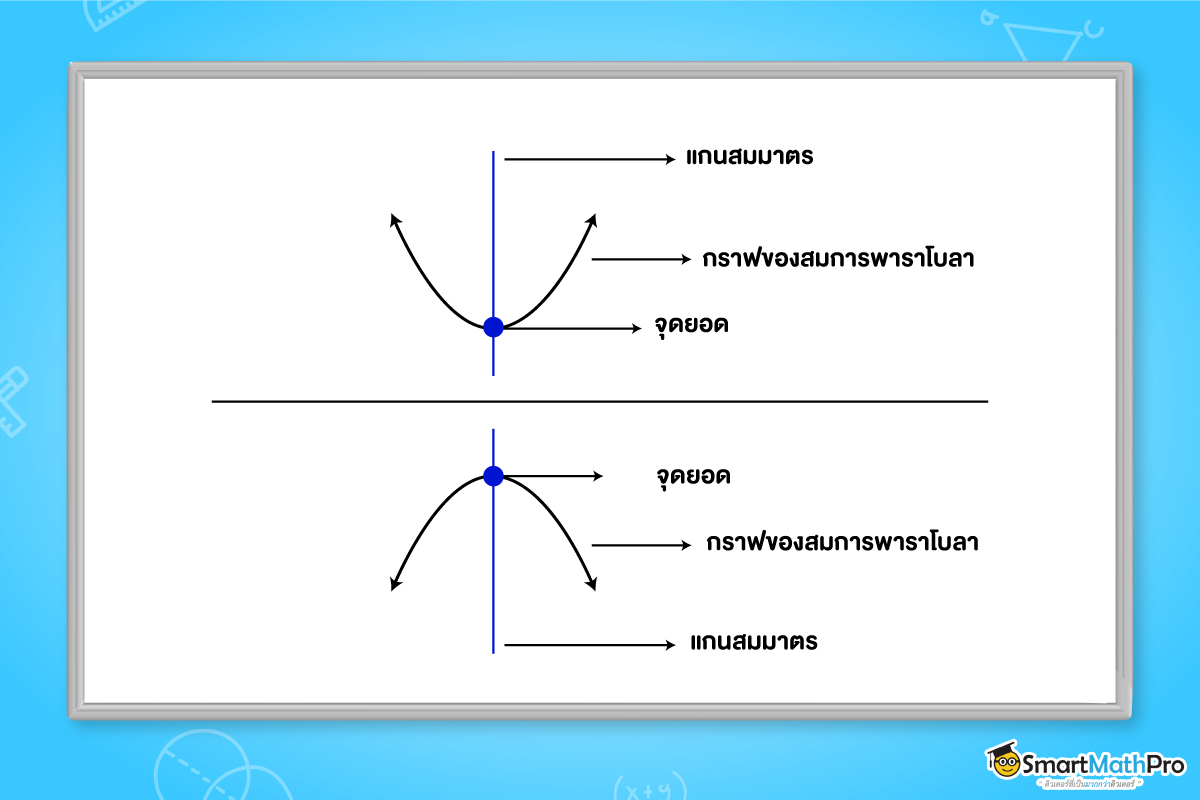
พาราโบลาที่มีจุดยอดอยู่ที่ (0,0)
พอเรารู้ส่วนประกอบของพาราโบลาไปแล้ว ต่อไปเราจะมาดูกันว่ากราฟพาราโบลาที่มีจุดยอดอยู่ที่ \left ( 0,0 \right ) จะมีสมการของพาราโบลา หรือฟังก์ชันกำลังสองที่มีหน้าตาของสมการเป็นยังไง พาราโบลาจะคว่ำ หรือหงายตอนไหน รวมถึงการสังเกตความแคบหรือความบานของกราฟด้วยว่าความแตกต่างกันนั้น เกิดจากค่าไหนของสมการ
พาราโบลาที่มีจุดยอดอยู่ที่จุด \left ( 0,0 \right ) คือพาราโบลาที่มีสมการอยู่ในรูป y=ax^{2}
โดยเราจะบอกลักษณะของกราฟได้จากค่า a
ตัวอย่างที่ 2
จงบอกลักษณะสำคัญของกราฟพาราโบลาของสมการ y=\frac{1}{2}x^2
วิธีทำ พิจารณาสมการของพาราโบลา เนื่องจาก a=\frac{1}{2} ซึ่ง a>0
ดังนั้น กราฟจะมีลักษณะเป็นพาราโบลาหงาย และกราฟจะมีจุดต่ำสุด อยู่ที่ \left ( 0,0 \right) แต่ไม่มีจุดสูงสุด โดยมีค่าต่ำสุดของ y คือ 0
โดยความบานของกราฟ จะมากหรือน้อยก็ขึ้นอยู่กับค่า a เช่นเดียวกัน ถ้า \left | a \right | มีค่าน้อยลงเรื่อย ๆ กราฟจะบานมากขึ้นเรื่อย ๆ และถ้า \left | a \right | มีค่ามากขึ้นเรื่อย ๆ กราฟจะบานน้อยลงเรื่อย ๆ (กราฟดูแคบลง)
วิธีสังเกต คือ เลขเล็ก ๆ กราฟจะบาน เลขใหญ่ ๆ กราฟจะแคบ โดยไม่ต้องสนเครื่องหมายบวกลบ
และเราสามารถบอกได้ว่าพาราโบลานี้ จะมีแกนสมมาตรอยู่ที่แกน y หรือ x=0 เสมอนั่นเอง
ตัวอย่างที่ 3
จงจับคู่สมการของพาราโบลากับกราฟของสมการต่อไปนี้
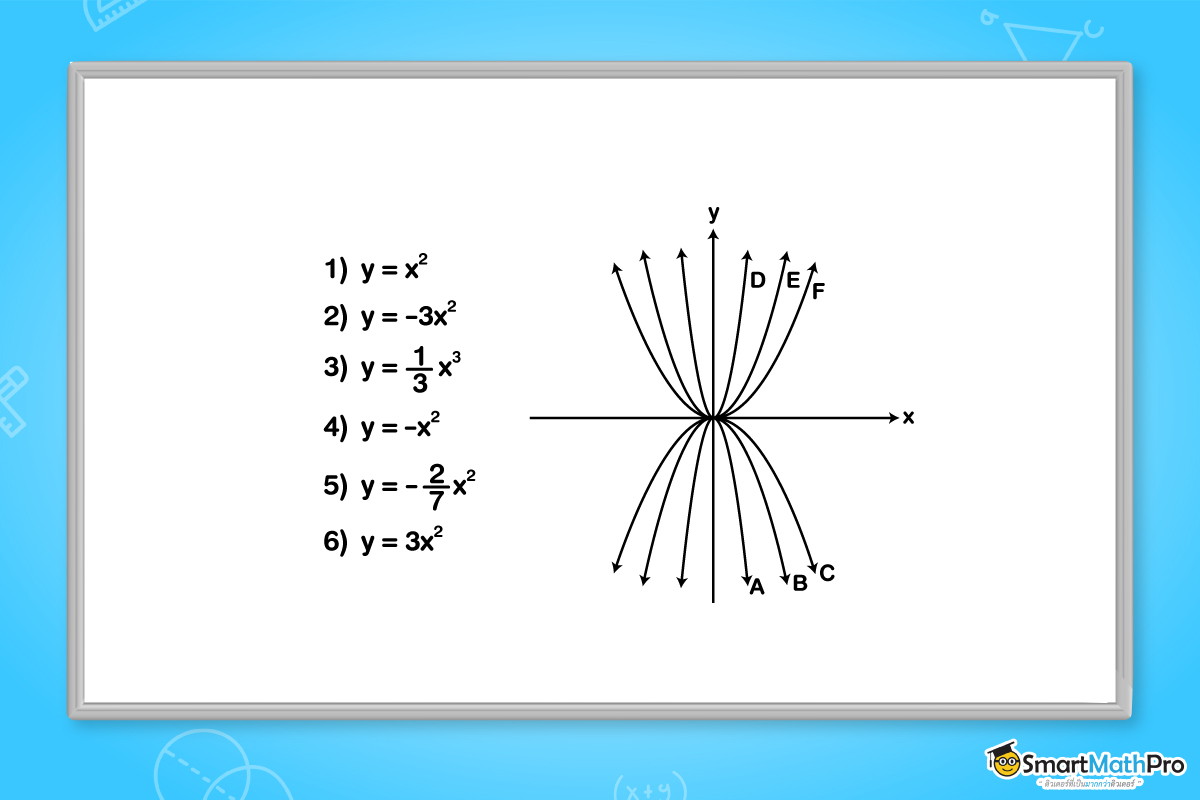
กลุ่มที่ 1
a>0
ได้แก่ สมการในข้อ 1 ข้อ 3 และข้อ 6
เนื่องจาก ถ้า \left | a \right | มีค่าน้อยลงเรื่อย ๆ กราฟจะบานมากขึ้นเรื่อย ๆ
จะได้ว่า พาราโบลา D เป็นกราฟของสมการในข้อ 6 คือ y={3x}^2
พาราโบลา E เป็นกราฟของสมการในข้อ 1 คือ y={x}^2
พาราโบลา F เป็นกราฟของสมการในข้อ 3 คือ y=\frac{1}{3}x^2
ได้แก่ สมการในข้อ 2 ข้อ 4 และข้อ 5
สมการพาราโบลา
จากเนื้อหาก่อนหน้านี้เราได้เห็นรูปแบบสมการของพาราโบลาในรูป y=ax^2 กันแล้ว ทีนี้มาดูกันว่าสมการพาราโบลามีรูปแบบสมการเป็นแบบไหนได้อีกบ้าง และกราฟที่ได้จากสมการแต่ละรูปแบบจะมีลักษณะที่แตกต่างกันยังไงด้วย
ตัวอย่างที่ 4
กำหนดค่า x ดังในตาราง จงเติมค่า y ที่สอดคล้องกับสมการที่กำหนดให้ลงในตารางให้ถูกต้อง พร้อมทั้งวาดกราฟของแต่ละสมการที่กำหนดให้
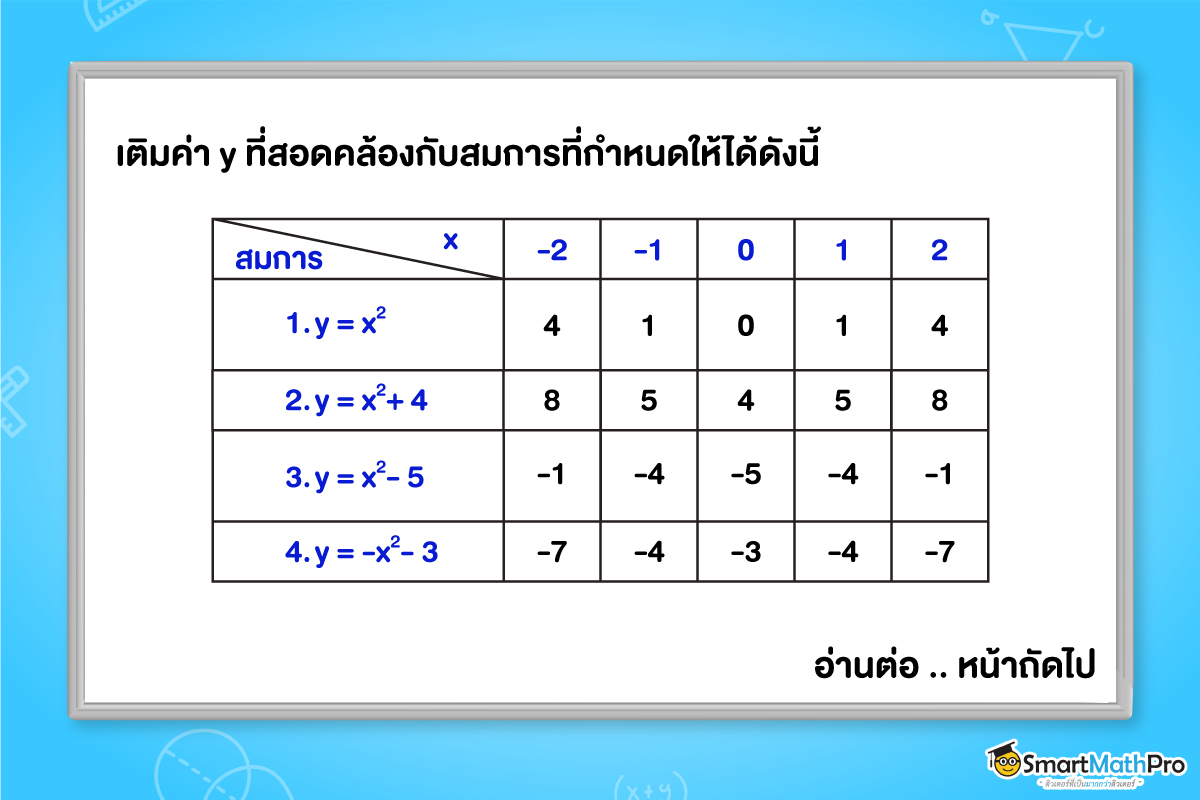
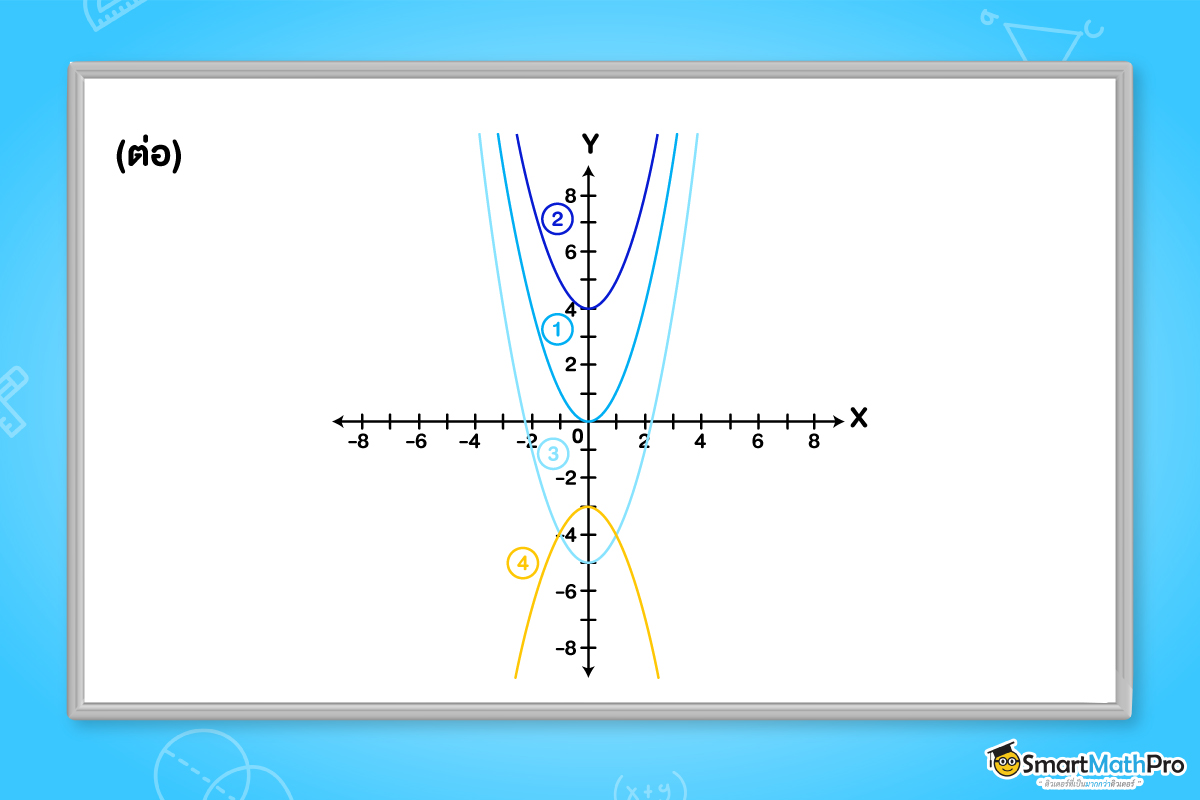
สังเกตว่า จุดยอดของกราฟจะอยู่ที่จุด (0,k) มีค่าสูงสุดหรือค่าต่ำสุดของ y เท่ากับ k และกราฟมีลักษณะการเปลี่ยนแปลง โดยการเลื่อนขึ้นหรือเลื่อนลงตามค่า k
ซึ่งสรุปได้ว่า
เมื่อ k>0 จะทำให้กราฟพาราโบลาเลื่อนขึ้น
และเมื่อ k<0 จะทำให้กราฟพาราโบลาเลื่อนลง
พาราโบลากำหนดด้วยสมการ y=a\left ( x-h \right )^2 เมื่อ a\neq 0 และ h\neq 0
กราฟที่กำหนดด้วยสมการรูปแบบนี้ จะเป็นพาราโบลาที่มีจุดยอดอยู่ที่ (h,0) และมีแกนสมมาตรคือ เส้นตรง x=h
ตัวอย่างที่ 5
กำหนดค่า x ดังในตาราง จงเติมค่า y ที่สอดคล้องกับสมการที่กำหนดให้ลงในตารางให้ถูกต้อง พร้อมทั้งวาดกราฟของแต่ละสมการที่กำหนดให้
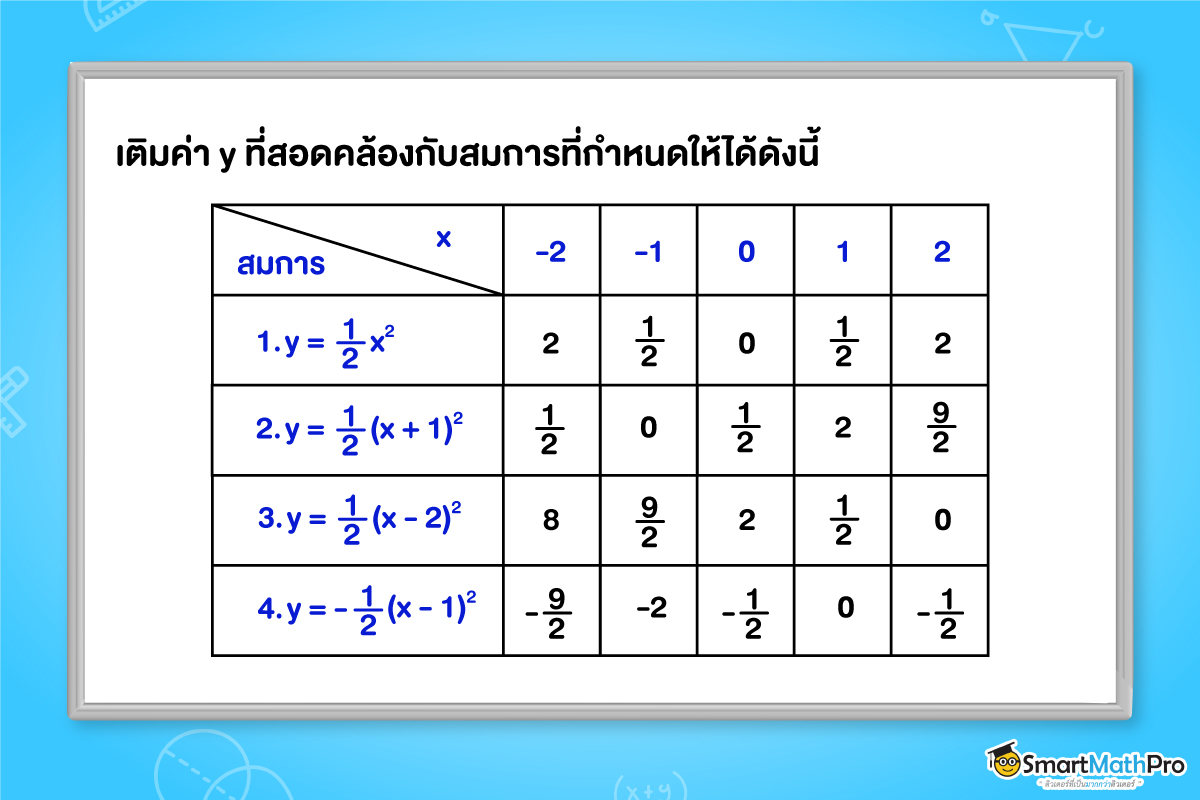
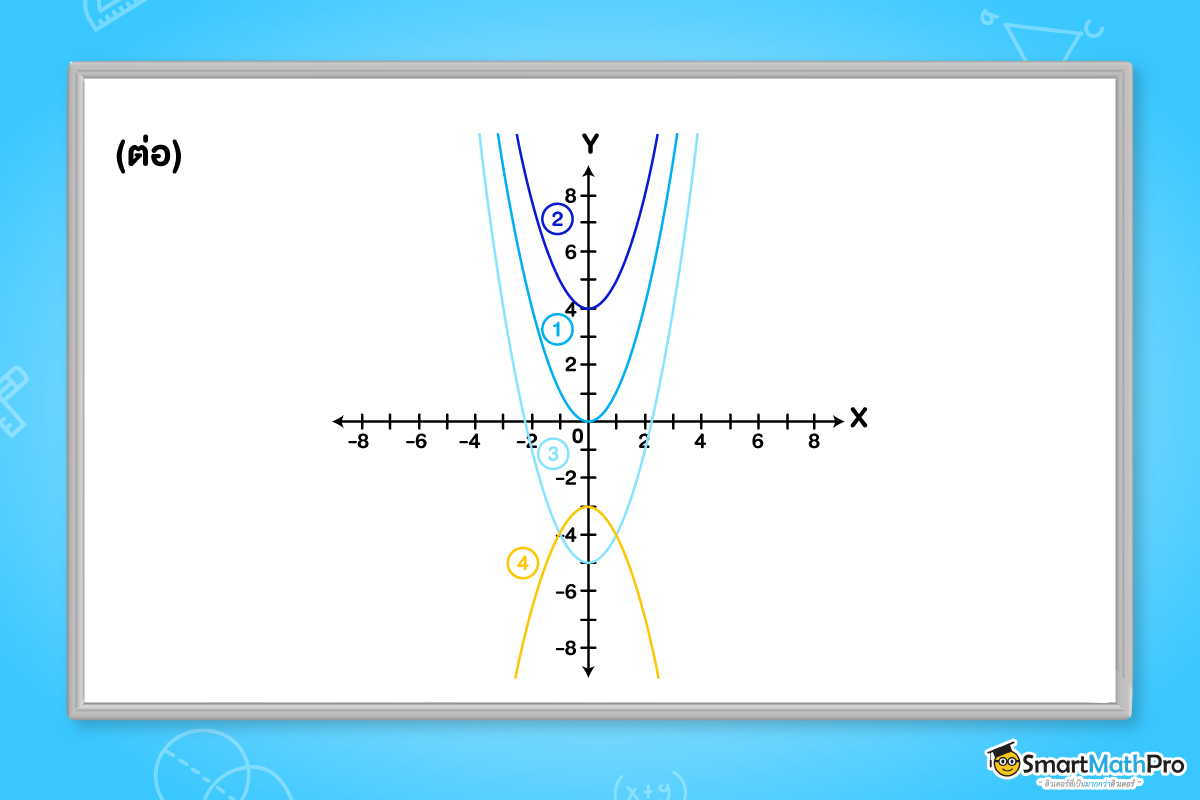
จากตัวอย่างนี้จะสังเกตได้ว่า จุดยอดของกราฟจะอยู่ที่จุด (h,0) และกราฟมีลักษณะการเปลี่ยนแปลงโดยการเลื่อนไปทางซ้ายหรือเลื่อนไปทางขวาตามค่า h
ซึ่งสรุปได้ว่า
เมื่อ h>0 จะทำให้กราฟพาราโบลาเลื่อนไปทางขวา
และเมื่อ h<0 จะทำให้กราฟพาราโบลาเลื่อนไปทางซ้าย
จาก สองตัวอย่างที่ผ่านมาถือเป็นรูปแบบย่อยเพื่อทำให้เราสังเกตค่าของ h และ k ว่าส่งผลยังไงกับกราฟของสมการพาราโบลา ทีนี้มาดูรูปแบบเต็ม ๆ ของมัน คือสมการพาราโบลาที่มีทั้งค่า h และ k กันดีกว่า
พาราโบลากำหนดด้วยสมการ y=a\left ( x-h \right )^2 +k เมื่อ a\neq 0, h \neq 0 และ k\neq 0
กราฟที่กำหนดด้วยสมการรูปแบบนี้ จะเป็นพาราโบลาที่มีจุดยอดอยู่ที่ (h, k) และมีแกนสมมาตรคือ เส้นตรง x=h
ตัวอย่างที่ 6
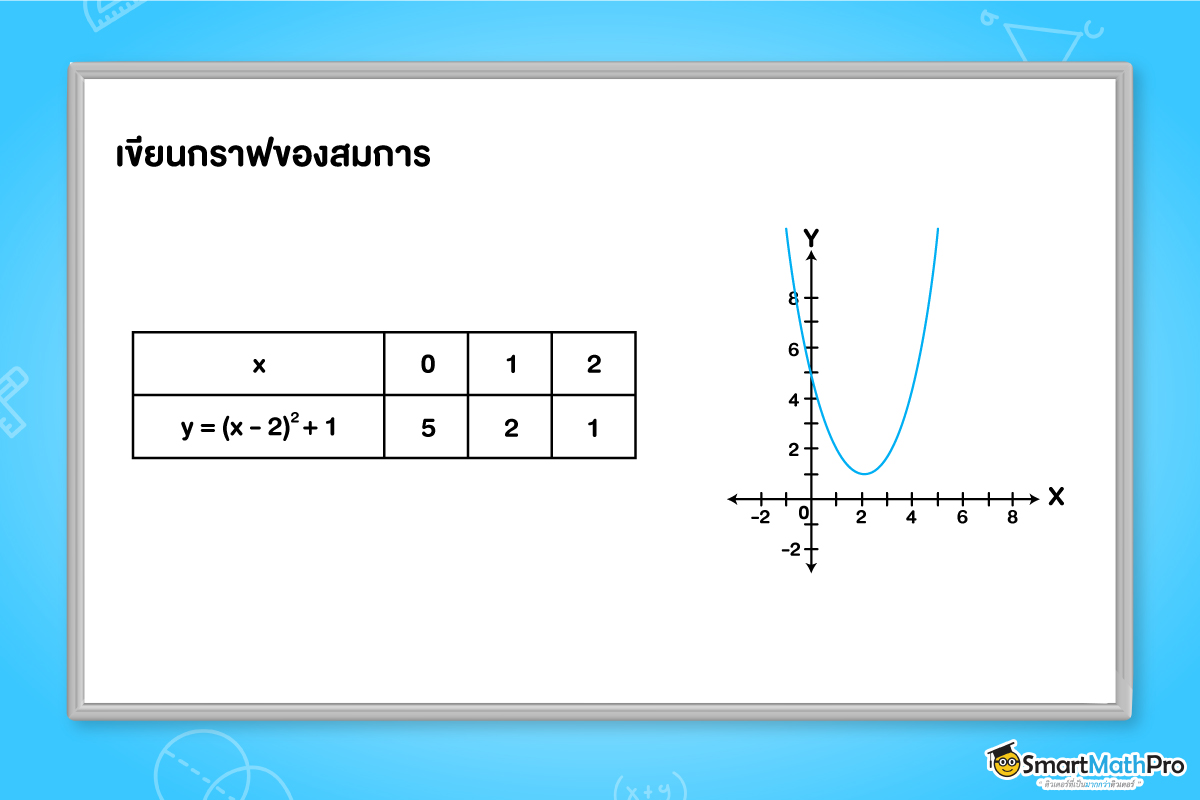
จงเขียนกราฟของสมการ
y=\left ( x-2 \right )^2 +1
วิธีทำ
พิจารณากราฟของสมการ
y=\left ( x-2 \right )^2 +1
จะได้
- กราฟเป็นพาราโบลาหงาย ที่มีเส้นตรง x=2 เป็นแกนสมมาตร
- จุดต่ำสุดของกราฟ คือ จุด (2,1)
- ค่าต่ำสุดของ y คือ 1
- หาพิกัดของจุดต่าง ๆ ที่อยู่ข้างเดียวกันของแกนสมมาตร
ตัวอย่างที่ 7
จงเขียนกราฟของสมการ
y=-2\left ( x+4 \right )^2 -5
วิธีทำ พิจารณากราฟของสมการ
y=-2\left ( x+4 \right )^2 -5
จะได้
- กราฟเป็นพาราโบลาคว่ำ ที่มีเส้นตรง x=-4 เป็นแกนสมมาตร
- จุดสูงสุดของกราฟ คือ จุด (-4,-5)
- ค่าสูงสุดของ y คือ -5
- หาพิกัดของจุดต่าง ๆ ที่อยู่ข้างเดียวกันของแกนสมมาตร
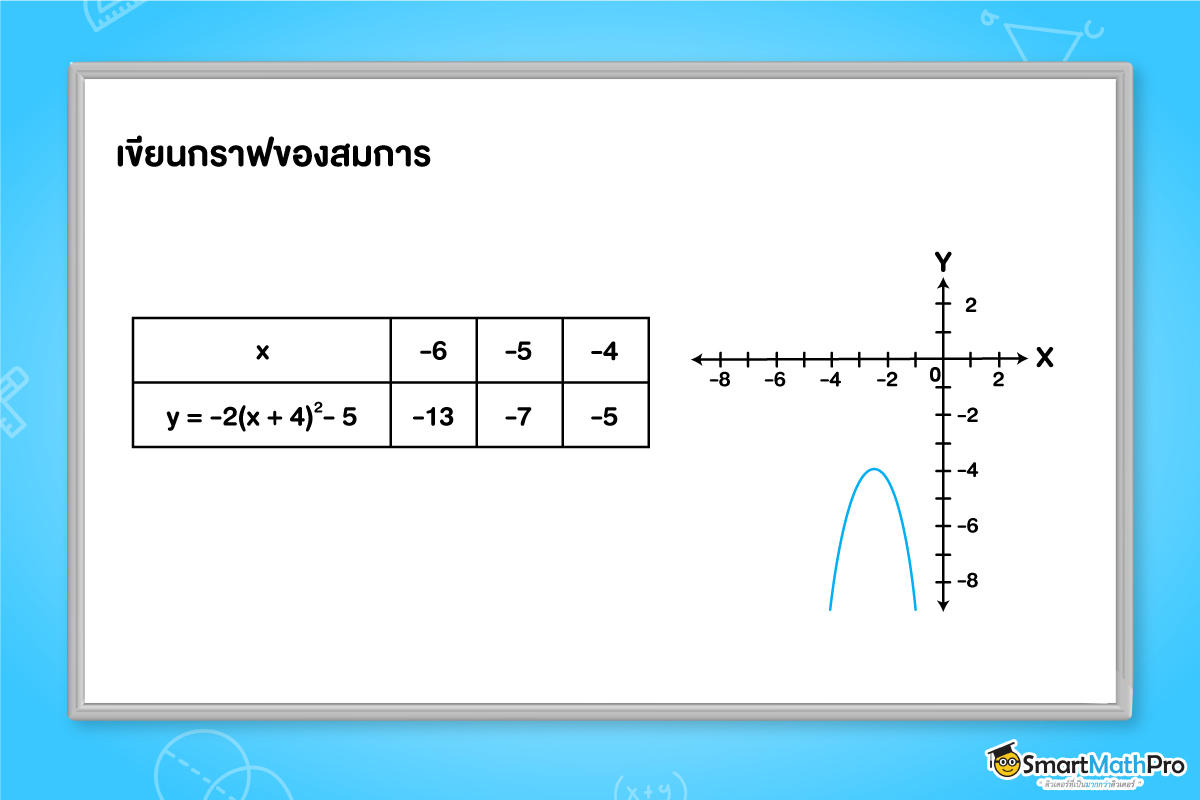
เขียนเส้นโค้งเรียบผ่านจุดพิกัดตามตาราง และเขียนเส้นโค้งเรียงที่สมมาตรกับอีกข้างหนึ่งของเส้นตรง x=-4
จะได้กราฟของสมการ y=-2\left ( x+4 \right )^2 -5
จากตัวอย่างที่ผ่านมาของสมการพาราโบลา เราสามารถสรุปได้ว่า
1. พาราโบลาที่กำหนดด้วยสมการ
y=a\left ( x-h \right )^2 +k เมื่อ a\neq 0
- ถ้า h=0 และ k=0
จะได้สมการ y=ax^2 - ถ้า h=0 และ k\neq 0
จะได้สมการ y=ax^2+k - ถ้า h\neq 0 และ k=0
จะได้สมการ y=a\left ( x-h \right )^2 - ถ้า h\neq 0 และ k\neq 0
จะได้สมการ y=a\left ( x-h \right )^2 +k
2. พาราโบลากำหนดด้วยสมการ
y=ax^{2}+bx+c เมื่อ a\neq 0
ในกรณีที่สมการของพาราโบลาอยู่ในรูปแบบ y=ax^{2}+bx+c จะมีปัญหาว่ารูปแบบดังกล่าวจะนำไปวาดกราฟของพาราโบลาและหาส่วนประกอบต่าง ๆ ของพาราโบลาได้ยาก แต่น้อง ๆ ไม่ต้องกังวลน้าา เราจะจัดรูปสมการนี้ใหม่เพื่อให้สมการอยู่ในรูปแบบของ y=a\left ( x-h \right )^2 +k ที่เพิ่งผ่านมาก่อนหน้า แล้วเราก็จะวาดกราฟและหาส่วนประกอบของพาราโบลาจากสมการที่จัดใหม่ได้เลยย
ตัวอย่างที่ 8
จงพิจารณาสมการ y = x^2 – 2x + 4 แล้วตอบคำถามต่อไปนี้
- กราฟเป็นพาราโบลาคว่ำหรือพาราโบลาหงาย
- จุดสูงสุดหรือจุดต่ำสุดของกราฟเป็นจุดใด
- เส้นตรงใดเป็นแกนสมมาตร
จะเห็นว่าวิธีการเบื้องต้นจะมีขั้นตอนที่ใช้ความรู้ในบทการแยกตัวประกอบของพหุนาม เรื่องการจัดพหุนามดีกรีสองให้อยู่ในรูปกำลังสองสมบูรณ์เข้ามาช่วย แน่นอนว่าบางคนเห็นแล้วก็อาจจะรู้สึกว่ามันยากเกินไป มีวิธีที่ง่ายกว่านี้ไหม พี่ก็ขอ
บอกเลยว่า มีน้าา และเป็นวิธีที่ไม่จำเป็นต้องจัดรูปกำลังสองสมบูรณ์ของพหุนามด้วย แค่น้อง ๆ รู้สูตรด้านล่างนี้ก็เอาไปปรับใช้ได้เลยย
สูตรลัดในการหาจุดยอดของพาราโบลา
ตัวอย่างที่ 9
จงพิจารณาสมการ y=2x^2-12x+19 แล้วตอบคำถามต่อไปนี้
- กราฟเป็นพาราโบลาคว่ำหรือพาราโบลาหงาย
- จุดสูงสุดหรือจุดต่ำสุดของกราฟเป็นจุดใด
- เส้นตรงใดเป็นแกนสมมาตร
ความเชื่อมโยงระหว่างพาราโบลาของ ม.ต้น และ ม.ปลาย
และน้อง ๆ ก็จะเห็นอีกว่า กราฟพาราโบลาที่เราเรียนตอนนี้เป็นกราฟที่เกิดจากฟังก์ชันกำลังสองซึ่งอยู่ในรูป y=ax^2+bx+c แต่กราฟพาราโบลาที่จะได้เจอในอนาคตนั้นยังมีนิยามอื่น ๆ อีกที่นอกเหนือจากรูปแบบของฟังก์ชัน ซึ่งเราจะได้รู้จัักกับสมการของพาราโบลาที่ทำให้เกิดกราฟแบบตะแคงขวาและตะแคงซ้ายในบทภาคตัดกรวยด้วยย
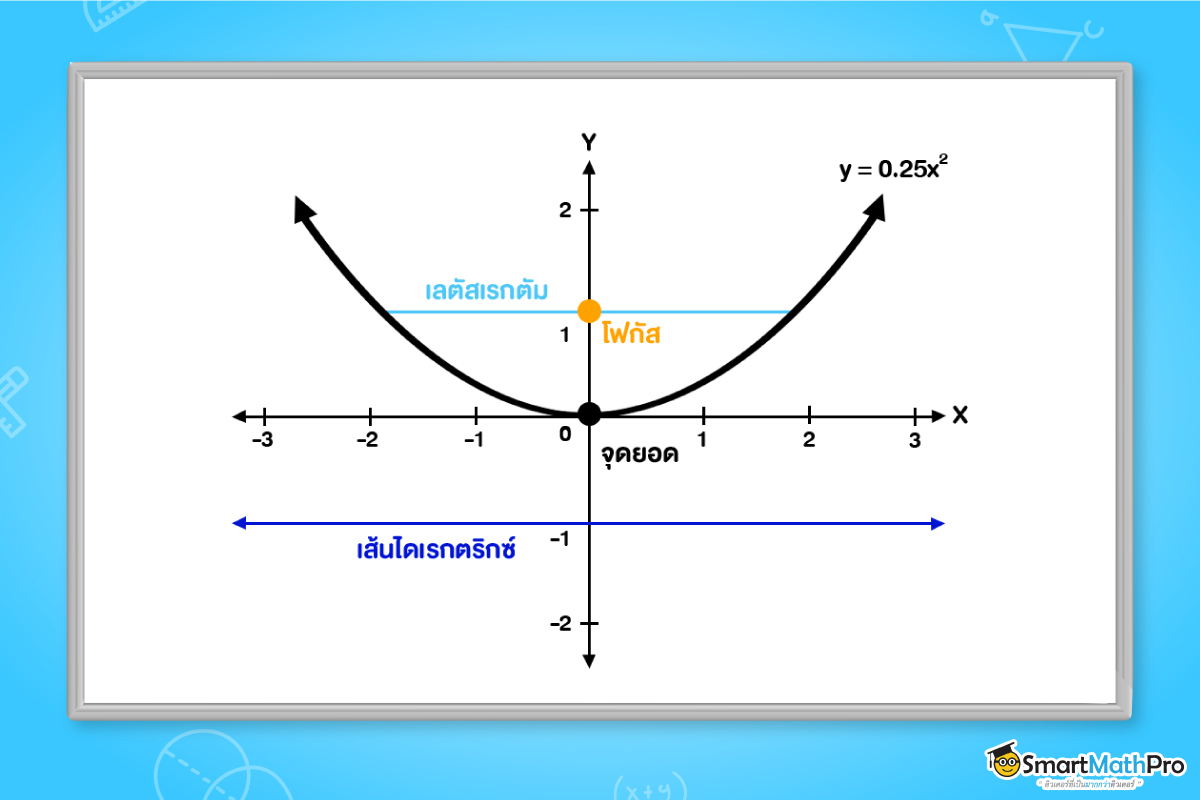
และเราอาจจะเคยเจอในชีวิตประจำวันมาบ้างแล้ว แต่อาจจะนึกไม่ถึงว่าเกี่ยวกับพาราโบลายังไง รวมไปถึงเราจะได้รู้จักและทำความเข้าใจส่วนประกอบต่าง ๆ ของพาราโบลา ไม่ว่าจะเป็น จุดโฟกัส เส้นไดเรกตริกซ์ ลาตัสเรกตัม โดยหน้าตาของพาราโบลาแบบตะแคงที่พี่ได้พูดไปเมื่อกี้ มีตัวอย่างประกอบตามรูปข้างล่างเลยย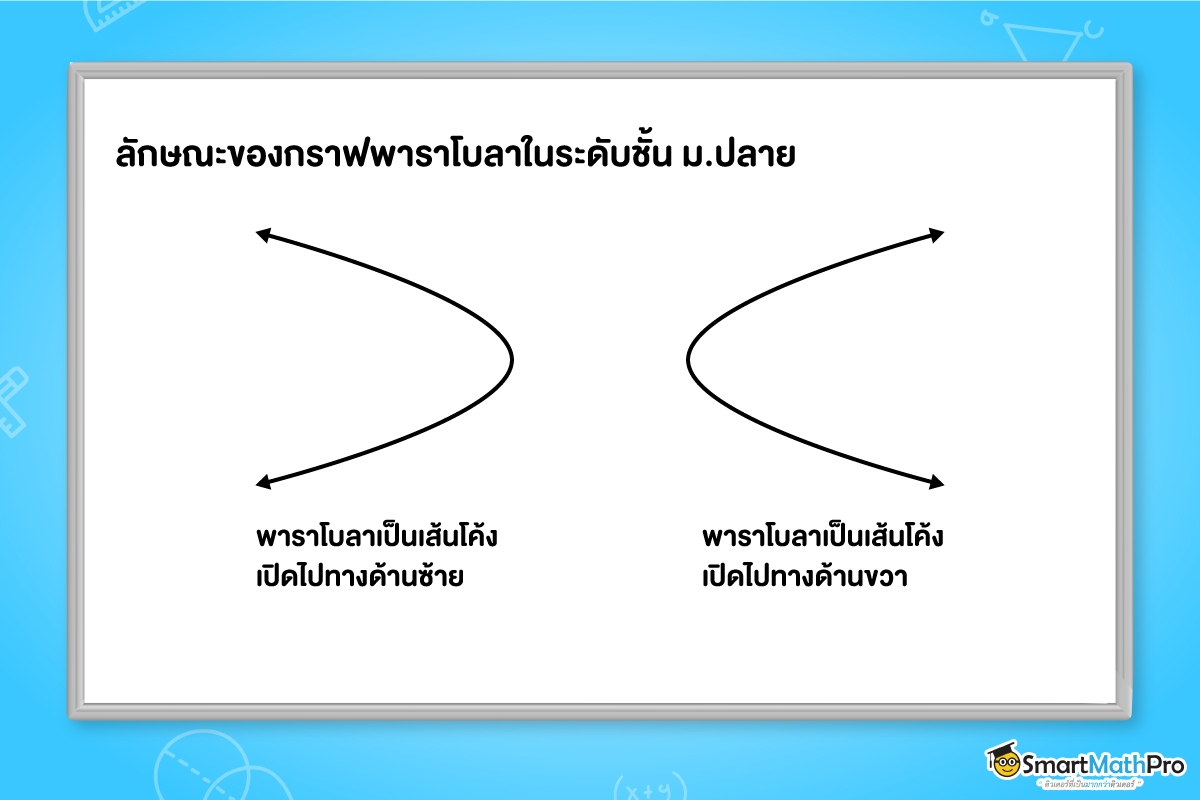
เป็นยังไงกันบ้างงง กับเนื้อหาคณิตศาสตร์ ม.3 เรื่องพาราโบลา (ฟังก์ชันกำลังสอง) ที่น้อง ๆ เพิ่งอ่านจบไป จะเห็นว่าเป็นบทที่ไม่ได้มีแค่สูตร สมการ หรือการคำนวณอย่างเดียว แต่มีการวาดกราฟเข้ามาเกี่ยวด้วยย ซึ่งจะเอาไปต่อยอดกับเนื้อหาคณิต ม.ปลาย ได้อีกเยอะเลยย และถ้าใครอ่านจบแล้ว อยากลองทดสอบความเข้าใจของตัวเอง ก็สามารถดาวน์โหลดแบบฝึกหัดไปลองทำกันได้เลยน้าา >>> แจกฟรี แบบฝึกหัดพาราโบลา (ฟังก์ชันกำลังสอง) ม.3
เนื้อหาคณิต ม.3 ถือว่าเป็นบทเรียนที่ยากสุดของคณิต ม.ต้นเลย สำหรับใครที่ลองทบทวนหรือฝึกทำโจทย์เองแล้ว แต่ยังมีเนื้อหาบางจุดที่ยังไม่เข้าใจ ต้องการคนช่วยไกด์เนื้อหาให้เข้าใจมากขึ้น พี่ขอแนะนำคอร์สติวคณิต ม.3 จาก SmartMathPro เลยย คอร์สนี้มีทั้งเนื้อหาของทั้งเทอม 1 และเทอม 2 ครบทุกบท ซึ่งพี่จะปูพื้นฐานให้แบบละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. พร้อมพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ แถมยังมี Quiz ทบทวนความเข้าใจแต่ละบทให้ด้วยน้า ดังนั้นใครที่พื้นฐานไม่แน่นก็เรียนได้ ไม่ต้องกังวลเลยว่าจะเรียนไม่ทัน !!
แต่ถ้าโรงเรียนของน้อง ๆ สอนไม่ตรงตามคอร์สที่มี ก็สามารถเลือกเรียนแบบแยกบทได้เลยย เริ่มต้นเพียง 360 บาทเท่านั้น ใครสนใจดูรายละเอียดเพิ่มเติม คลิก ได้เลย
ดูคลิปติว พาราโบลา (ฟังก์ชันกำลังสอง) ม.3
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง Youtube Channel : SmartMathPro
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
สรุป แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 พร้อมโจทย์+เฉลย
สรุป อสมการเชิงเส้นตัวแปรเดียว ม.3 พร้อมแจกโจทย์และเฉลย
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สถิติ ม.3 สรุปเนื้อหาคณิตม.ต้นหลักสูตรใหม่ พร้อมแจกโจทย์ให้ลองทำ !
สรุป วงกลม ม.3 ทฤษฎีบทวงกลม พร้อมแจกแบบฝึกหัดฟรี !
ตรีโกณมิติ ม.3 สรุปเนื้อหาพร้อมโจทย์แบบจัดเต็ม จบในที่เดียว !
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
