ถ้าพูดถึงสมการ พี่ว่าทุกคนต้องร้องอ๋อกันแน่นอน เพราะเป็นเนื้อหาที่น้อง ๆ ต้องเคยเรียนผ่านกันมาบ้างแล้วใน
วิชาคณิต แต่รู้ไหมว่ายังมีอีกเรื่องหนึ่งที่แม้จะชื่อคล้ายกันแต่ไม่ใช่เรื่องเดียวกันอยู่ด้วยน้า ซึ่งเรื่องนั้นก็คือ อสมการ
เชิงเส้นตัวแปรเดียว นั่นเองงง โดยวันนี้พี่จะพาทุกคนไปหาคำตอบกันว่า อสมการเชิงเส้นตัวแปรเดียวคืออะไร
ซึ่งพี่ได้สรุปเนื้อหา พร้อมทั้งโจทย์ให้น้อง ๆ ได้ฝึกทำไปด้วยกัน ถ้าทุกคนพร้อมแล้วเราไปลุยกันเลยยย
ทบทวนความรู้ก่อนเรียนเรื่องอสมการ
ก่อนเราจะเริ่มสรุปเนื้อหาบทอสมการเชิงเส้นตัวแปรเดียว พี่จะพาน้อง ๆ มาทบทวนความรู้เดิมกันก่อน นั่นก็คือ ความรู้เกี่ยวกับเครื่องหมายที่ใช้ในสมการและอสมการ สมบัติของการเท่ากัน และเส้นจำนวน ถ้าพร้อมแล้วมาเริ่มกันเลย !!
เครื่องหมาย
> แทนความสัมพันธ์ น้อยกว่า
< แทนความสัมพันธ์ มากกว่า
≤ แทนความสัมพันธ์ น้อยกว่าหรือเท่ากับ
≥ แทนความสัมพันธ์ มากกว่าหรือเท่ากับ
≠ แทนความสัมพันธ์ ไม่เท่ากับ
สมบัติของการเท่ากัน
ให้ a, b และ c แทนจำนวนจริง
- สมบัติสมมาตร
ถ้า a=b แล้ว b=a - สมบัติถ่ายทอด
ถ้า a=b และ b=c แล้ว a=c - สมบัติของการเท่ากัน (การบวก)
ถ้า a=b แล้ว a+c=b+c - สมบัติของการเท่ากัน (การคูณ)
ถ้า a=b แล้ว ac=bc
เส้นจำนวน
อสมการเชิงเส้นตัวแปรเดียว คืออะไร ?
ก่อนที่เราจะมาพูดถึงความหมายของอสมการเชิงเส้นตัวแปรเดียว เรามาเริ่มดูที่คำว่า “อสมการ” กันก่อน
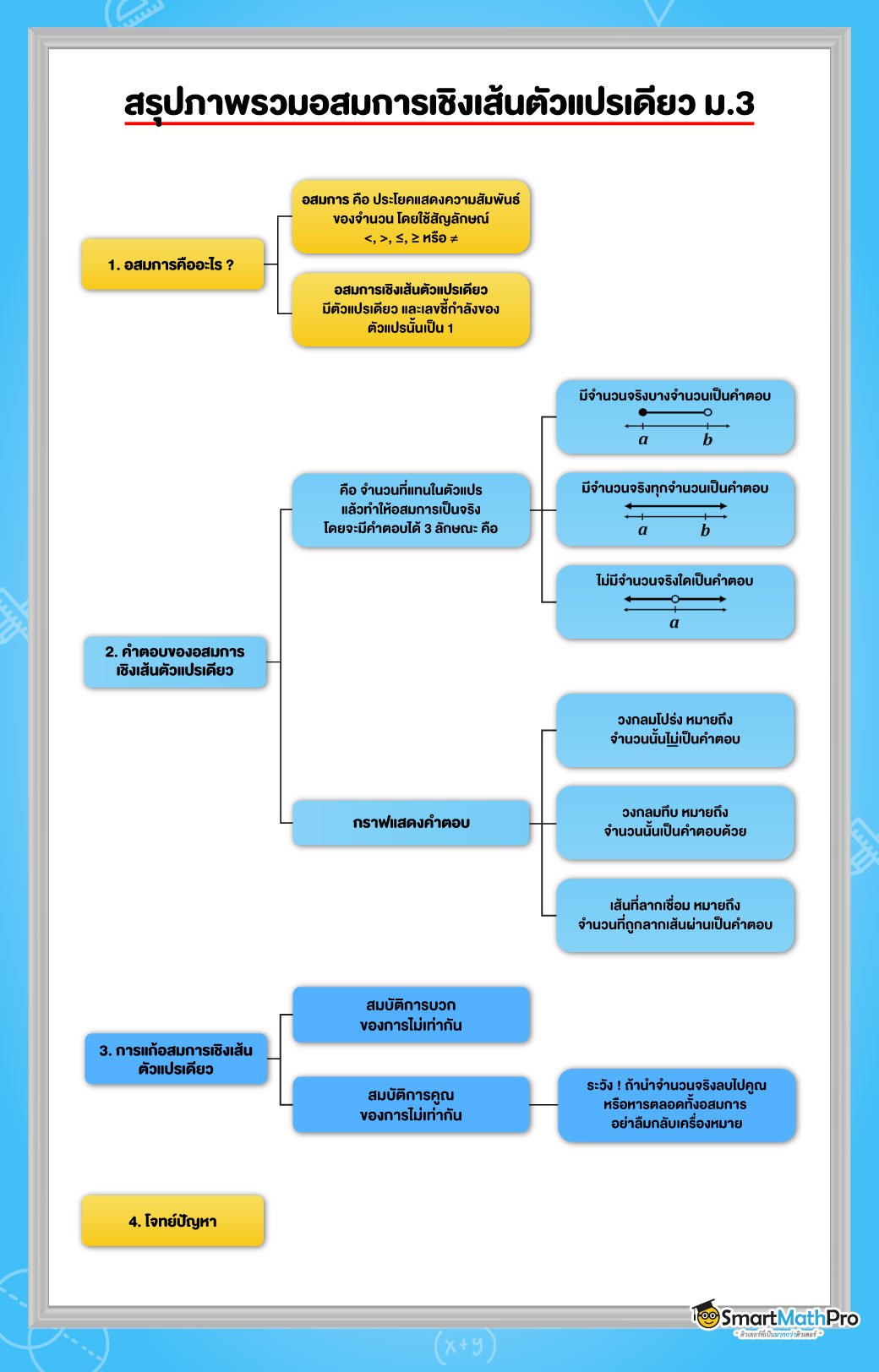
อสมการ คือ ประโยคแสดงความสัมพันธ์ของจำนวน โดยใช้สัญลักษณ์ <, >, ≤, ≥ หรือ ≠
ตัวอย่างของอสมการ
- 2x+1>2
- x-2y\leq x^2
- k-2 \neq k^2
- 2x+1<x-3<-x+2
อสมการเชิงเส้นตัวแปรเดียว คือ อสมการที่มีตัวแปรเพียงตัวเดียว (มีหลายจุดได้แต่ต้องเป็นตัวแปรเดียวกัน) และ เลขชี้กำลังของตัวแปรนั้นต้องเป็น 1 เสมอ
ดังตัวอย่างต่อไปนี้
คำตอบของอสมการเชิงเส้นตัวแปรเดียว
โดยอสมการจะมีคำตอบได้ 3 ลักษณะ คือ
- มีจำนวนจริงบางจำนวนเป็นคำตอบ
- มีจำนวนจริงทุกจำนวนเป็นคำตอบ
- ไม่มีจำนวนจริงใดเป็นคำตอบ
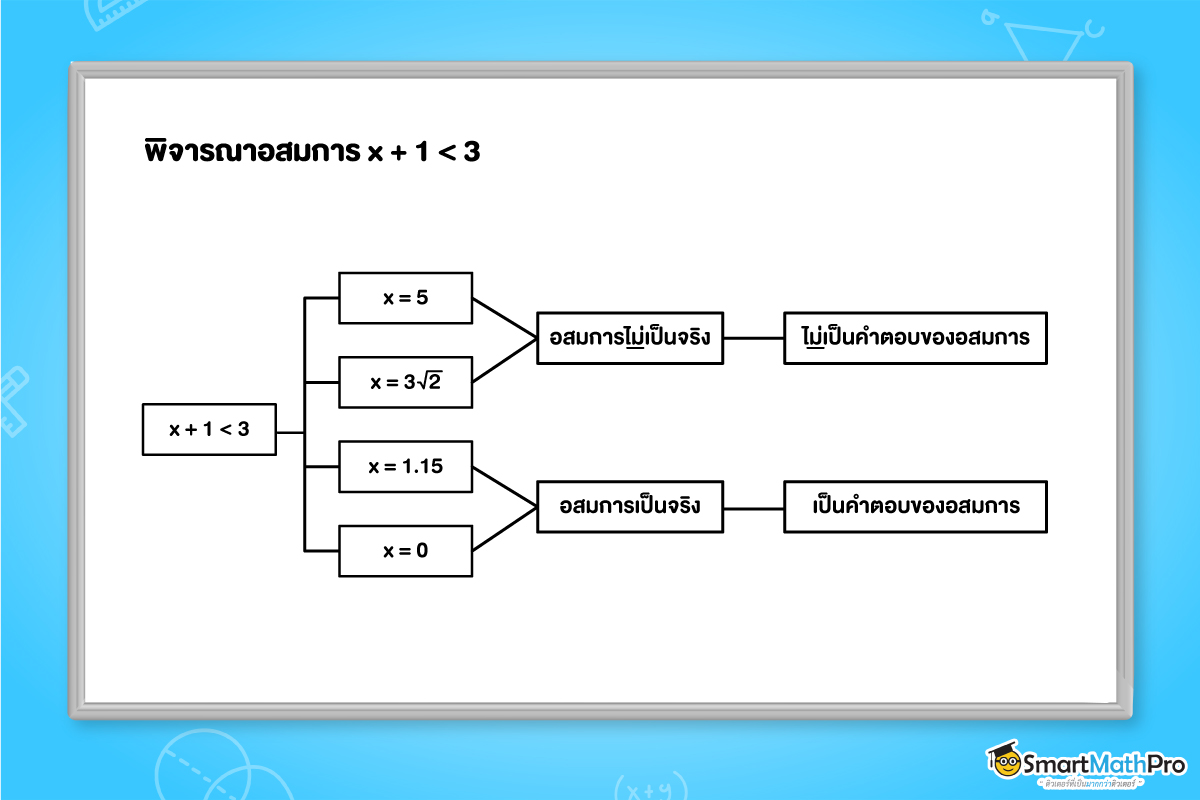
ถ้าน้อง ๆ ต้องการพิจารณาว่าจำนวนจริงนั้นเป็นคำตอบของอสมการไหม ให้ลองนำจำนวนจริงที่ว่าแทนค่าลงไปในอสมการดู ถ้าอสมการเป็นจริง แสดงว่าจำนวนจริงนั้นเป็นคำตอบของอสมการ แต่ถ้าแทนค่าลงไปแล้วอสมการไม่เป็นจริง ก็แสดงว่าจำนวนจริงนั้นไม่เป็นคำตอบของอสมการ
กราฟแสดงคำตอบของอสมการ
การเขียนกราฟแสดงคำตอบของอสมการประกอบด้วย 3 ส่วนที่สำคัญ ดังนี้
- วงกลมโปร่ง หมายถึง จำนวนนั้นไม่เป็นคำตอบ
- วงกลมทึบ หมายถึง จำนวนนั้นเป็นคำตอบด้วย
- เส้นทึบที่ลากเชื่อม หมายถึง จำนวนที่เป็นไปได้ทั้งหมดที่เป็นคำตอบของอสมการ โดยใช้การลากเส้นผ่านจำนวนนั้น ๆ
การแก้อสมการเชิงเส้นตัวแปรเดียว
ใช้สมบัติของการไม่เท่ากัน (properties of inequality) ในการหาคำตอบ
สมบัติการบวกของการไม่เท่ากัน
ให้ a และ b แทนจำนวนจริงใด ๆ
- ถ้า a < b แล้ว a+c < b+c
- ถ้า a > b แล้ว a+c > b+c
- ถ้า a \leq b แล้ว a+c\leq b+c
- ถ้า a\geq b แล้ว a+c\geq b+c
สมบัติการคูณของการไม่เท่ากัน
ให้ a, b แทนจำนวนจริงใด ๆ และ c แทนจำนวนจริงบวก
- ถ้า a < b แล้ว ac < bc
- ถ้า a\leq b แล้ว ac \leq bc
- ถ้า a > b แล้ว ac > bc
- ถ้า a \geq b แล้ว ac \geq bc
ให้ a, b แทนจำนวนจริงใด ๆ และ c แทนจำนวนจริงลบ
- ถ้า a < b แล้ว ac > bc
- ถ้า a \leq b แล้ว ac \geq bc
- ถ้า a > b แล้ว ac < bc
- ถ้า a \geq b แล้ว ac \leq bc
จากสมบัติข้างต้น ถ้าลองสังเกตสมบัติการคูณของการไม่เท่ากัน เมื่อคูณจำนวนจริงลบเข้าไปตลอดทั้งอสมการจะต้องกลับเครื่องหมายด้วยนะ ส่วนการบวก (ทั้งจำนวนจริงบวกและลบ) และการคูณด้วยจำนวนจริงบวก ตลอดทั้งอสมการ
ไม่ต้องกลับเครื่องหมายน้าา
หลังจากที่เรารู้จักกับสมบัติของการไม่เท่ากันแล้ว เราลองนำสมบัติไปใช้แก้อสมการกัน !!
การแก้โจทย์ปัญหา
ขั้นตอนการแก้โจทย์ปัญหาอสมการเชิงเส้นตัวแปรเดียว
การแก้โจทย์ปัญหาอสมการเชิงเส้นตัวแปรเดียว สามารถทำได้ในทำนองเดียวกับการแก้สมการเชิงเส้นตัวแปรเดียว
โดยมีขั้นตอนดังนี้
ขั้นที่ 1 วิเคราะห์โจทย์เพื่อหาว่าโจทย์กำหนดอะไรมาให้ และให้หาอะไร
ขั้นที่ 2 กำหนดตัวแปรแทนสิ่งที่โจทย์ให้หา หรือแทนสิ่งที่เกี่ยวข้องกับสิ่งที่โจทย์ให้หา
ขั้นที่ 3 เขียนอสมการตามเงื่อนไขในโจทย์
ขั้นที่ 4 แก้อสมการเพื่อหาคำตอบที่โจทย์ต้องการ
ขั้นที่ 5 ตรวจสอบคำตอบที่ได้กับเงื่อนไขในโจทย์
ตัวอย่างที่ 2 เจด้ามีเหรียญห้าบาทและสองบาทรวมกันได้ 10 เหรียญ คิดเป็นเงินรวมแล้วไม่ถึง 40 บาท เจด้ามีเหรียญห้าบาทมากที่สุดกี่เหรียญ
วิธีทำ
ขั้นที่ 1 โจทย์กำหนดให้
– เจด้ามีเหรียญห้าบาทและสองบาทรวมกันได้ 10 เหรียญ
– เงินที่เจด้ามีรวมแล้วไม่ถึง 40 บาท
ขั้นที่ 2 ให้ x แทน จำนวนเหรียญห้าบาท
– จะได้ว่า เจด้ามีเหรียญสองบาท จำนวน 10 – x เหรียญ
ดังนั้น เจด้ามีเหรียญห้าบาทรวม 5x บาท และ เหรียญสองบาทรวม 2(10 – x) บาท
ขั้นที่ 3 จากเงินที่เจด้ามีรวมแล้วไม่ถึง 40 บาท เขียนอสมการได้ว่า
– 5x + 2 (10 – x) < 40
ขั้นที่ 4 แก้อสมการเพื่อหาคำตอบที่โจทย์ต้องการ
5x + 2 (10 – x) < 40
5x + 20 – 2x < 40
3x + 20 < 40
3x < 40 – 20
3x < 20
x<\frac{20}{3}
ขั้นที่ 5 ตรวจสอบคำตอบ
แทน x = 6 ในอสมการ 5x + 2 (10 – x ) < 40
จะได้ดังนี้
(5)(6) + 2 (10 – (6)) < 40
30 + 2 (4) < 40
30 + 8 < 40
38 < 40
ดังนั้น อสมการเป็นจริง
ตอบ เจด้ามีเหรียญ 5 บาทมากที่สุด 6 เหรียญ
ดูคลิปติวเรื่อง "อสมการเชิงเส้นตัวแปรเดียว ม.3"
ดูคลิปติวฟรีอื่น ๆ เพิ่มเติมได้ที่ YouTube : SmartMathPro
เป็นยังไงกันบ้างงง เนื้อหาอสมการเชิงเส้นตัวแปรเดียวที่พี่เอามาให้ทุกคนวันนี้ พอไหวกันไหม ? หลายคนอาจจะรู้สึกว่ามันยาก แต่จริง ๆ แล้วทุกคนยังไม่จำเป็นต้องเข้าใจทั้งหมดในวันนี้ก็ได้น้าา ค่อย ๆ ทบทวนเนื้อหาควบคู่ไปกับการฝึกทำโจทย์ เราก็จะเก่งขึ้นเองง ซึ่งพี่ก็เตรียม แบบฝึกหัดอสมการเชิงเส้นตัวแปรเดียว ม.3 มาให้ทุกคนดาวน์โหลดไปลองฝึกทำ
แต่ถ้าใครที่ลองทบทวนหรือฝึกทำโจทย์เองแล้วยังมีเนื้อหาบางจุดที่ยังไม่เข้าใจ ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้
ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์
พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.3 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากกก) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก เลย
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
ตรีโกณมิติ ม.3 สรุปเนื้อหาพร้อมโจทย์แบบจัดเต็ม จบในที่เดียว !
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
