มีน้อง ๆ คนไหนกำลังเรียนอยู่ชั้น ม.3 หรืออยู่ในช่วงกำลังจะขึ้น ม.3 แล้วอยากได้สรุปเนื้อหาคณิตมาทบทวนกันบ้างงง ? วันนี้ห้ามพลาดเลยน้า เพราะวันนี้พี่มีเนื้อหาคณิต ม.3 เรื่อง การแยกตัวประกอบของพหุนามที่มีดีกรีสูงกว่าสอง
มาฝากทุกคน !!
นอกจากนี้ที่ท้ายบทความยังมีคลิปติวที่สอนโดยพี่ปั้น แถมยังแจกแบบฝึกหัดพร้อมเฉลยให้น้อง ๆ เอาไปฝึกทำกันด้วย ใครอยากเข้าใจเนื้อหาเรื่องนี้มากขึ้น ก็รีบเลื่อนลงไปดูกันเล้ยยย
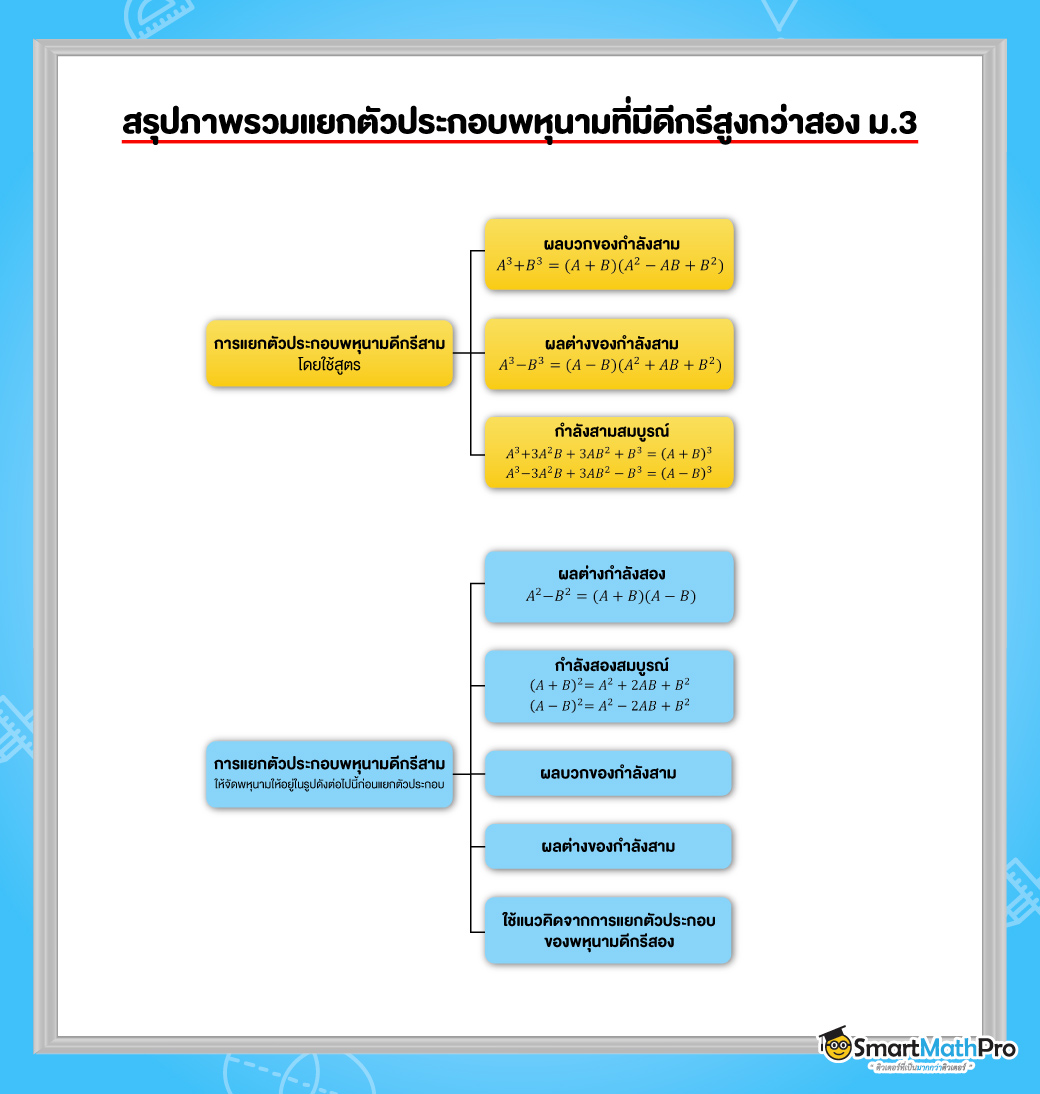
ในระดับชั้น ม.2 น้อง ๆ เคยเรียนเกี่ยวกับการแยกตัวประกอบพหุนามดีกรีสองมาแล้ว จากชื่อของบทนี้จะเห็นว่าพหุนามที่เราจะแยกตัวประกอบมีดีกรีสูงขึ้นกว่าที่เคยเรียนมา ดังนั้นเรามาทบทวนความหมายกันก่อนน้าา
พหุนาม
คือ นิพจน์ที่อยู่ในรูปการบวกกันของเอกนามตั้งแต่สองเอกนามขึ้นไปได้ เช่น
- x^{3} + 8
- x^{2} – 2x – 1
ดีกรีของพหุนาม
คือ ดีกรีสูงสุดของพจน์ของพหุนามในรูปผลสำเร็จ เช่น
- 2x – 1 เป็นพหุนามที่มีดีกรีเท่ากับ 1
- 4x^{3} – x^{2} + 1 เป็นพหุนามที่มีดีกรีเท่ากับ 3
การแยกตัวประกอบพหุนาม
คือ การเขียนพหุนามที่กำหนดให้อยู่ในรูปของการคูณกันของพหุนามตั้งแต่สองพหุนามขึ้นไป เช่น
- 10x^{3} + 5x แยกตัวประกอบได้เป็น (5x)(2x² + 1)
- x^{4} – 3^{2}+x แยกตัวประกอบได้เป็น (x)(x^{3} + 3x + 1)
จากตัวอย่างอย่างข้างต้นจะเห็นว่าเราสามารถแยกตัวประกอบของ 5x^{3} + x ซึ่งเป็นพหุนามดีกรีสาม
และ x^{4} + 3x^{2} + x ซึ่งเป็นพหุนามดีกรีสี่ได้ด้วยวิธีการดึงตัวร่วม
คำถามคือ ถ้าเป็นพหุนามดีกรีสาม หรือตั้งแต่สามขึ้นไป (ตามชื่อบท นั่นคือเราจะมาแยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสองกัน) ที่ไม่สามารถแยกตัวประกอบด้วยวิธีดึงตัวร่วมได้อย่างเช่นตัวอย่างด้านล่างนี้
- x^{3} + 8
- x^{3} + 6x^{2} +12x + 8
- x^{4} + 2x^{2} – 3
- x^{3}y^{6} – 8
จะแยกตัวประกอบอย่างไรดี ? ในบทเรียนนี้จะมีคำตอบให้น้อง ๆ เลย เราสามารถใช้สูตรต่าง ๆ หรือใช้ความรู้เดิมนั่นคือการแยกตัวประกอบพหุนามดีกรีสอง (แยกสองวงเล็บ) มาใช้ต่อยอดได้นะ
การแยกตัวประกอบพหุนามดีกรีสาม
หัวข้อนี้จะกล่าวถึงการแยกตัวประกอบพหุนามดีกรีสาม ที่แต่ละพจน์มีสัมประสิทธิ์และค่าคงตัวเป็นจำนวนเต็ม ซึ่งพหุนามจะอยู่ในรูปของผลบวกและผลต่างของกำลังสาม รวมถึงกำลังสามสมบูรณ์ ซึ่งจะมีวิธีการแยกตัวประกอบโดยใช้สูตรดังนี้
ผลบวกและผลต่างของกำลังสาม
พหุนามต่อไปนี้ ถ้าน้องสังเกตเห็นว่าเป็นพหุนามที่น่าจะเขียนให้อยู่ในรูปผลบวกของกำลังสาม A^{3} + B^{3} หรือผลต่างของกำลังสาม A^{3} – B^{3} ได้ ให้ลองจัดรูปดู
ถ้ามีตัวไหนที่ไม่ได้อยู่ในรูปของกำลังสามของจำนวนนั้นหรือตัวแปรนั้นให้เขียนให้เรียบร้อย เช่น 8 คือกำลังสามของ 2 และ 27y^{3} คือกำลังสามของ 3y ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 1 จงแยกตัวประกอบของพหุนามดีกรีสามต่อไปนี้
1) x^{3} + 8
วิธีทำ จาก x^{3} + 8 แยกตัวประกอบได้ดังนี้
x^{3} + 8 = x^{3} + x^{2}
= (x + 2) (x^{2} – (x)(2)+2^{2})
= (x + 2) (x^{2} – 2x + 4)
ดังนั้น x^{3} + 8 แยกตัวประกอบได้เป็น (x + 2) (x^{2} – 2x + 4)
2) 27y^{3} – 125
วิธีทำ จาก 27y^{3} – 125 แยกตัวประกอบได้ดังนี้
27y^{3} – 125 = (3y^{3}) – 5^{3}
= (3y – 5) \left [(3y)^{2} + (3y)(5) + 5^{2} \right ]
= (3y – 5) (9y^{2} + 15y + 25)
ดังนั้น 27y^{3} – 125 แยกตัวประกอบได้เป็น = (3y – 5) (9y^{2} + 15y + 25)
กำลังสามสมบูรณ์
พหุนามต่อไปนี้ ถ้าน้องสังเกตเห็นว่าเป็นพหุนามที่น่าจะเขียนให้อยู่ในรูป A^{3} + 3A^{2}B + 3AB^{2} + B^{3} หรือ A^{3} – 3A^{2}B + 3AB^{2} – B^{3} ได้ นั่นคือลองเขียนพจน์แรกและท้ายสุดให้อยู่ในรูปของกำลังสาม เพื่อหาว่าจากโจทย์ A และ B มีค่าเท่าใด จากนั้นตรวจสอบพจน์ตรงกลางสองพจน์ โดยใช้ A และ B ที่ได้มาพิจารณาว่าสามารถเขียนให้อยู่ในรูป 3A^{2}B และ 3AB^{2} ได้หรือไม่ ถ้าได้ พหุนามที่โจทย์กำหนดคือพหุนามที่อยู่ในรูปกำลังสามสมบูรณ์
ตัวอย่างที่ 2 จงแยกตัวประกอบของพหุนามต่อไปนี้
1) x^{3} + 6x^{2} + 12x + 8
วิธีทำ จาก x^{3} + 6x^{2} + 12x + 8 แยกตัวประกอบได้ดังนี้
จะได้ x^{3} + 6x^{2} + 12x + 8 = x^{3} + 3 (x^{2})(2) + 3(x)(2^{2}) + 2^{3}
จากสูตร A^{3} + 3A^{2}B + 3AB^{2} + B^{3} = (A+B)^{3}
จะได้ A = x และ B = 2
ดังนั้น x^{3} + 6x^{2} + 12x + 8 = (x + 2)^{3}
นั่นคือ x^{3} + 6x^{2} + 12x + 8 แยกตัวประกอบได้เป็น (x + 2)^{3}
2) x^{3} + 9x^{2} + 27x – 27
วิธีทำ จาก x^{3} + 9x^{2} + 27x – 27 แยกตัวประกอบได้ดังนี้
จะได้ x^{3} + 9x^{2} + 27x – 27 = x^{3} – 3(x^{2})(3) + 3(x) (3^{2}) – 3^{3}
จากสูตร A^{3} + 3A^{2}B + 3AB^{2} + B^{3} = (A – B)^{3}
จะได้ A = x และ B = 2
ดังนั้น x^{3} + 9x^{2} + 27x – 27 = (x – 3)^{3}
นั่นคือ x^{3} + 9x^{2} + 27x – 27 แยกตัวประกอบได้เป็น (x – 3)^{3}
การแยกตัวประกอบพหุนามดีกรีสูงกว่าสาม
การแยกตัวประกอบของพหุนามที่มีดีกรีสูงกว่าสาม อาจทำได้โดยจัดพหุนามให้อยู่ในรูปผลต่างของกำลังสอง กำลังสองสมบูรณ์ ผลบวกกำลังสาม ผลต่างกำลังสาม หรือใช้แนวคิดของการแยกตัวประกอบพหุนามดีกรีสอง
จัดให้อยู่ในรูปผลต่างของกำลังสอง
ตัวอย่างที่ 3 จงแยกตัวประกอบของพหุนาม x^{4}-16
วิธีทำ จากรูปแบบของผลต่างกำลังสอง A^{2} – B^{2} = (A + B)(A – B) แยกตัวประกอบได้ดังนี้
จะได้ x^{4}-16 = (x^{2})^{2} – (4^{2})
= (x^{2} + 4) (x^{2} – 4)
= (x^{2} + 4) (x^{2} – 2^{2})
= (x^{2} + 4) (x + 2) (x – 2)
เนื่องจาก x^{2} + 4 ไม่สามารถแยกตัวประกอบต่อได้
ดังนั้น x^{4}-16 แยกตัวประกอบได้เป็น (x^{2} + 4) (x + 2) (x – 2)
จัดให้อยู่ในรูปกำลังสองสมบูรณ์
ตัวอย่างที่ 4 จงแยกตัวประกอบของพหุนาม x^{4} + 32x^{2} + 256
วิธีทำ กำหนดให้ K = x^{2}
จากรูปแบบของกำลังสองสมบูรณ์ A^{2} + 2AB + B^{2} = (A+B)^{2} แยกตัวประกอบได้ดังนี้
จะได้ x^{4} + 32x^{2} + 256 = (x^{2})^{2} + 32x^{2} + 256
= K^{2} + 32K + 256
= K^{2} + 2(16)K+ 16^{2}
= (K + 16)^{2}
= (x^{2} + 16)^{2}
ดังนั้น x^{4} + 32x^{2} + 256 แยกตัวประกอบได้เป็น (x^{2} + 16)^{2}
ข้อสังเกต ! สามารถสมมติตัวแปรเป็น K ได้นะ เพื่อให้เรามองพหุนามดีกรีสี่เป็นพหุนามดีกรีสองได้ จะได้แยกตัวประกอบได้ง่ายขึ้น แต่อย่าลืมเปลี่ยน K กลับมาเป็น x ด้วยนะ
จัดให้อยู่ในรูปผลบวกของกำลังสาม หรือผลต่างของกำลังสาม
ตัวอย่างที่ 5 จงแยกตัวประกอบของพหุนาม x^{3}y^{6}-8
วิธีทำ จากรูปแบบของผลต่างกำลังสาม A^{3} – B^{3} = (A – B) (A^{2} + AB + B^{2}) แยกตัวประกอบได้ดังนี้
จะได้ x^{3}y^{6} – 8 = (xy^{2})^{3} – 2^{3}
= [xy^{2} – 2] \left [(xy^{2})^{2} + (xy^{2})(2) + 2^{2} \right ]
= (xy^{2} – 2)(x^{2})y^{4} + 2xy^{2} + 4)
ดังนั้น x^{3}y^{6} – 8 แยกตัวประกอบได้เป็น (xy^{2} – 2)(x^{2})y^{4} + 2xy^{2} + 4)
ใช้แนวคิดจากการแยกตัวประกอบของพหุนามดีกรีสอง
ทบทวนแนวคิดการแยกพหุนามดีกรีสองโดยแยกเป็นสองวงเล็บ
พหุนามที่อยู่ในรูป ax^{2} + bx + c แยกตัวประกอบเป็น
(px + r)(qx + 8) เมื่อ pq = a, rs = c และ ps + qr = b โดยที่ a, b, c, p, q, r, s เป็นจำนวนเต็ม และ a ≠ 0
เช่น
x^{2} + x – 2 = (x – 1)(x + 2)
6x^{2} – 11x + 3 = (3x – 1)(2x – 3)
จากตัวอย่างข้างต้น ถ้าเราสามารถเขียนพหุนามที่มีดีกรีสูงกว่าสองนี้ให้อยู่ในรูปของพหุนามดีกรีสองได้ โดยอาจสมมติตัวแปรเป็น K เช่นที่เคยทำในตัวอย่างก่อนหน้า แล้วเราก็จะแยกตัวประกอบของพหุนามดีกรีสูงกว่าสองเป็นสองวงเล็บได้เช่นกัน
สามารถเปรียบเทียบการแยกตัวประกอบของพหุนามดีกรีสอง ซึ่งเป็นความรู้เดิม โดยการแยกตัวประกอบของพหุนามโดยนำแนวคิดมาใช้ ดังนี้
การแยกตัวประกอบของพหุนามดีกรีสอง (ความรู้เดิม)
ตัวอย่างที่ 6 จงแยกตัวประกอบของพหุนาม x^{2} + 2x – 3
วิธีทำ
พิจารณา x^{2} + 2x – 3 = (x + 3)(x – 1)
ดังนั้น x^{2} + 2x – 3 แยกตัวประกอบได้เป็น (x + 3)(x – 1)
การแยกตัวประกอบของพหุนามดีกรีสูงกว่าสาม (นำแนวคิดมาใช้)
ตัวอย่างที่ 7 จงแยกตัวประกอบของพหุนาม x^{4}+2x^{2} – 3
วิธีทำ กำหนดให้ K = x^{2}
จะได้
x^{4} + 2x^{2} – 3 = (x^{2})^{2} + 2x^{2} – 3
= K^{2} + 2K – 3
= (K + 3)(K – 1)
= (x^{2} + 3)(x^{2} – 1)
= (x^{2} + 3)(x^{2} – 12)
= (x^{2} + 3)(x + 1)(x – 1)
ดังนั้น x^{4} + 2x – 3 แยกตัวประกอบได้เป็น (x^{2} + 3)(x + 1)(x – 1)
เป็นยังไงบ้างงง สำหรับสรุปเนื้อหาที่พี่เตรียมมาให้ มีทั้งคำอธิบาย บทนิยาม และตัวอย่างโจทย์เลย แต่ถ้าใครรู้สึกว่าตัวอย่างที่พี่ให้ยังน้อยไป อยากได้โจทย์มาซ้อมมือให้คล่อง ๆ มากกว่านี้ก็สามารถดาวน์โหลดแบบฝึกหัดการแยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 ไปฝึกทำกันได้เลยน้าา
ส่วนน้อง ๆ ที่รู้สึกการทบทวนหรือฝึกทำโจทย์เอง ยังไม่ค่อยช่วยให้เข้าใจมากขึ้นเท่าไร หรือยังมีบางจุดที่งง ๆ อยู่ เพราะเนื้อหาคณิต ม.3 ก็ถือว่าค่อนข้างยากที่สุดในคณิต ม.ต้น พี่ขอแนะนำคอร์สคณิต ม.3 จาก SmartMathpro เลยยย คอร์สนี้มีทั้งเนื้อหาของทั้งเทอม 1 และเทอม 2 ครบทุกบท ซึ่งพี่จะปูพื้นฐานให้แบบละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. พร้อมพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ แถมยังมี Quiz ทบทวนความเข้าใจแต่ละบทให้ด้วยน้า ดังนั้นใครที่พื้นฐานไม่แน่นก็เรียนได้ ไม่ต้องกังวลเลยว่าจะเรียนไม่ทัน !!
แต่ถ้าโรงเรียนของน้อง ๆ สอนไม่ตรงตามคอร์สที่มี ก็สามารถเลือกเรียนแบบแยกบทได้เลยย เริ่มต้นเพียง 360 บาทเท่านั้น ใครสนใจดูรายละเอียดเพิ่มเติม คลิก ได้เลย
ดูคลิปติว แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
สรุป อสมการเชิงเส้นตัวแปรเดียว ม.3 พร้อมแจกโจทย์และเฉลย
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สถิติ ม.3 สรุปเนื้อหาคณิตม.ต้นหลักสูตรใหม่ พร้อมแจกโจทย์ให้ลองทำ !
สรุป ฟังก์ชันกำลังสอง (พาราโบลา) ม.3 พร้อมแจกสูตรและโจทย์ฟรี
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
