น้อง ๆ บางคนพอได้ยินชื่อ “จำนวนจริง” ก็อาจจะสงสัยว่า เป็นการเรียนเกี่ยวกับตัวเลขที่เรารู้จักกันอยู่แล้วในชีวิต
ประจำวันหรือเปล่า ? ซึ่งพี่ขอบอกว่า นั่นเป็นเพียงแค่ส่วนหนึ่งของจำนวนจริงเท่านั้นน้าา เพราะในบทนี้เราจะมาทำความรู้จักจำนวนจริงให้มากขึ้นไปอีก ตั้งแต่ ความหมายของจำนวนจริง ระบบจำนวนจริง พหุนาม ค่าสัมบูรณ์ และเรื่องอื่น ๆ อีกมากมายที่กำลังรอทุกคนอยู่ แถมยังมีตัวอย่างโจทย์, ข้อสอบแจกฟรีและคลิปติว จำนวนจริง ม.4 ให้เข้าใจมากขึ้นด้วย ถ้าพร้อมแล้วก็เลื่อนลงไปอ่านกันเลยยย
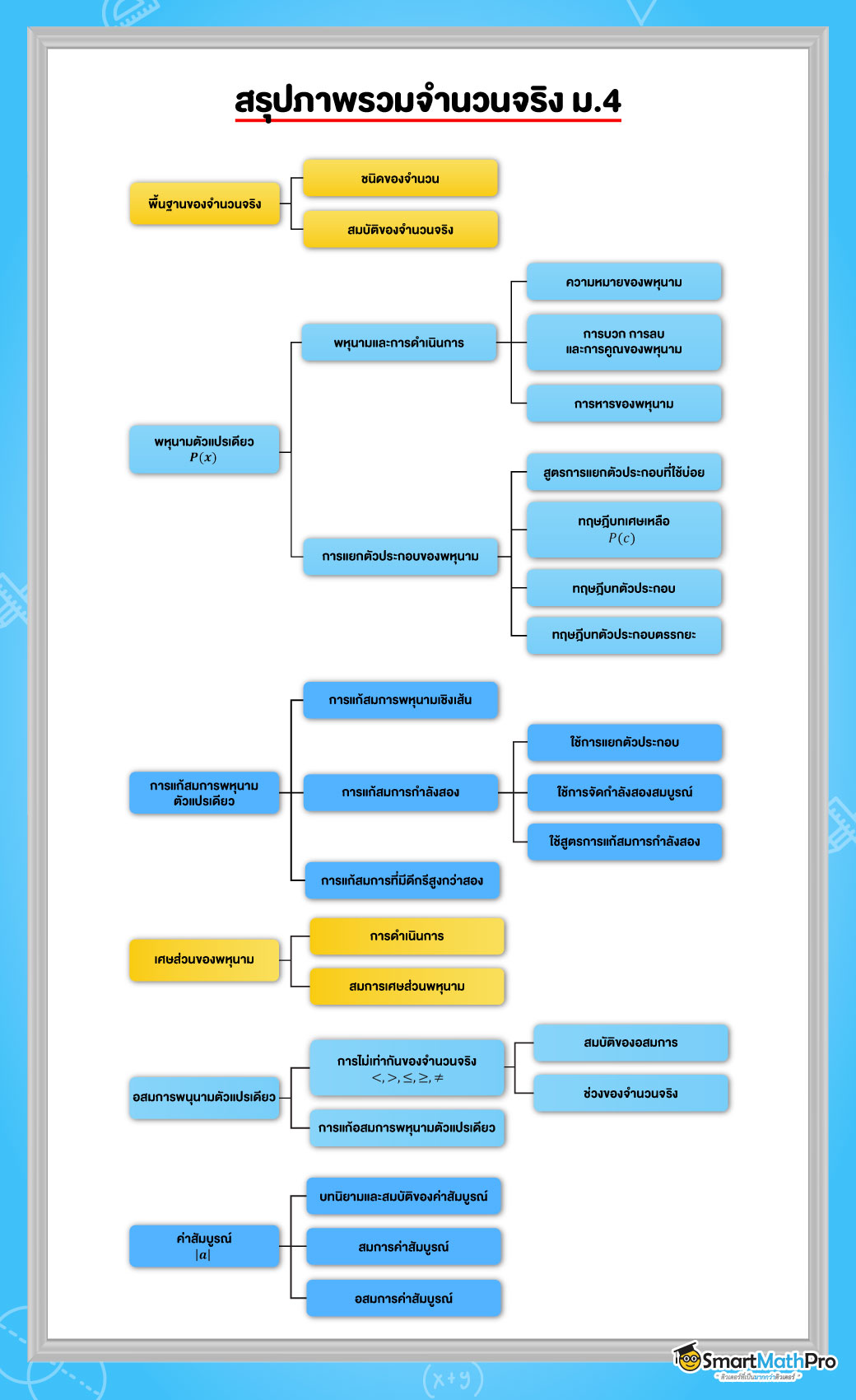
จำนวนจริงคืออะไร
สำหรับบท จำนวนจริง นั้น เป็นบทที่ชื่อดูเข้าใจง่ายหน่อย ถ้าถามว่าบทนี้ง่ายไหม อันนี้ต่างคนอาจจะตอบแตกต่างกัน แต่ถ้าถามว่าสำคัญไหม พี่พูดได้เลยว่าสำคัญมากน้า เพราะจำนวนเป็นสิ่งสำคัญของวิชาคณิตศาสตร์เลย
แต่เดี๋ยวในบทความนี้ น้อง ๆ จะได้เห็นว่าแล้วต้องเรียนอะไรเกี่ยวกับจำนวนจริงบ้าง แม้ว่าจะเคยผ่านการเรียนบทระบบจำนวนจริงตอน ม.2 มา แต่ในครั้งนี้จะมีหัวข้อใหม่ ๆ ให้เรียนรู้มากมายทีเดียว อาจจะเนื้อหาเยอะสักหน่อยแต่ไม่ต้องกลัว เพราะทุกหัวข้ออาศัยความรู้ที่เคยเรียนแล้วทั้งนั้น ถึงน้อง ๆ จะลืมไปแล้วก็ไม่เป็นไรน้า ค่อย ๆ เรียนรู้ไปด้วยกัน !
ก่อนอื่นมาเริ่มด้วยคำถามว่า จำนวนจริงคืออะไร ถ้าเอาแบบเข้าใจง่าย ๆ ก็คือ จำนวนทุกจำนวนที่รู้จักและสามารถนำมาคำนวณ บวก ลบ คูณ หาร ยกกำลังได้ ไม่ว่าจะเป็นจำนวนเต็ม เศษส่วน ทศนิยม เลขยกกำลัง ตัวเลขที่อยู่ในรูปกรณฑ์ (ที่เรียกกันติดปากว่า รูท) หรือค่าคงที่อย่าง \pi ก็เป็นจำนวนจริงเช่นกันนะ
คราวนี้ เพิ่มความซีเรียสกันขึ้นมาหน่อย พี่จะขอทบทวนจำนวนสองชนิด ได้แก่ จำนวนตรรกยะ และจำนวนอตรรกยะ ซึ่งความหมายและตัวอย่างของจำนวนแต่ละชนิดเป็นดังนี้
จำนวนตรรกยะ
คือ จำนวนที่เขียนในรูป \frac{a}{b} โดย a และ
b เป็นจำนวนเต็ม และ b\neq 0
นั่นคือจำนวนที่เขียนได้ในรูปเศษส่วนของจำนวนเต็ม หรือเขียนเป็นทศนิยมซ้ำได้
เช่น 7, 1.5, -\frac{5}{4}, 2.4\dot{3}, 0 เป็นต้น
จำนวนอตรรกยะ
คือ จำนวนที่เป็นทศนิยมแบบไม่ซ้ำ (และเป็นทศนิยมไม่รู้จบ ก็คือตัวเลขหลังทศนิยมไม่มีที่สิ้นสุดด้วย) ซึ่งจำนวนชนิดนี้ไม่สามารถเขียนเป็นเศษส่วนของจำนวนเต็มได้
เช่น \sqrt{2}, 1.121231234…, \pi, \sqrt[3]{4}, 1-\sqrt{2} เป็นต้น
จะเห็นว่า จำนวนตรรกยะ และจำนวนอตรรกยะ จะมีความแตกต่างกันชัดเจน มีลักษณะที่ตรงข้ามกัน นั่นแปลว่า เซตของจำนวนตรรกยะ และเซตของจำนวนอตรรกยะ จะไม่มีสมาชิกที่ซ้ำกันเลย อย่างไรก็ตาม ถ้านำเซตของจำนวนตรรกยะและเซตของจำนวนอตรรกยะมายูเนียน (รวมกัน) เราจะได้ผลลัพธ์จากการยูเนียนคือ เซตของจำนวนจริง นั่นเอง โดยจำนวนจริงสามารถแบ่งเป็นจำนวนชนิดต่างๆ ดังแผนผังต่อไปนี้
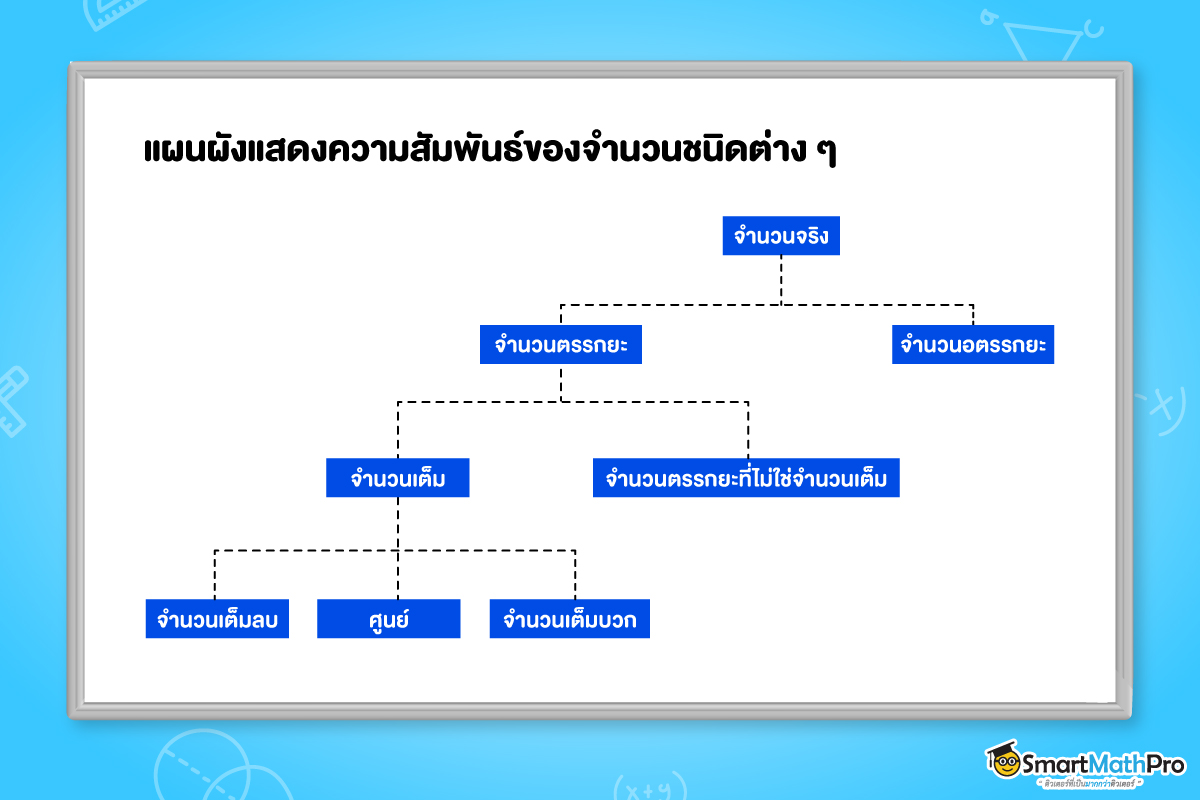
สัญลักษณ์ของเซตของจำนวนจริงชนิดต่าง ๆ ที่ควรรู้จัก ได้แก่
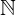แทนเซตของจำนวนเต็มบวก (จำนวนนับ)
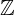แทนเซตของจำนวนเต็ม
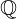แทนเซตของจำนวนตรรกยะ
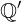แทนเซตของจำนวนอตรรกยะ
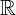แทนเซตของจำนวนจริง
ระบบจำนวนจริง
หัวข้อนี้เราจะมาศึกษาเกี่ยวกับโครงสร้างของระบบจำนวนจริงกัน ซึ่งประกอบด้วยเซตของจำนวนจริง และการดำเนินการของจำนวนจริง ประกอบด้วย การบวกและคูณ
แต่ก่อนจะเข้าหัวข้อระบบจำนวนจริง เราต้องมีข้อตกลงร่วมกันหรือสิ่งที่ทุกคนต้องยอมรับแบบไม่ต้องพิสูจน์ว่าจริงหรือไม่กันเสียก่อน เรียกว่า สัจพจน์การเท่ากันของระบบจำนวนจริง น้อง ๆ มาดูกันนะว่ามีอะไรบ้าง
สัจพจน์การเท่ากันของระบบจำนวนจริง
- สำหรับจำนวนจริง a, b และ c
กฎการสะท้อน (reflexive law)
a = a - กฎการสมมาตร (symmetric law)
ถ้า a=b แล้ว b=a - กฎการถ่ายทอด (transitive law)
ถ้า a=b และ b=c แล้ว a=c
คราวนี้กลับมาที่หัวข้อระบบจำนวนจริง จากที่พี่เขียนไว้ว่าหัวข้อนี้มีการดำเนินการของจำนวนจริงด้วย พี่ก็จะขอพูดถึงสมบัติของการดำเนินการ ได้แก่ สมบัติของการบวกและการคูณของจำนวนจริง ซึ่งมีสมบัติสำคัญทั้งหมดดังนี้
สมบัติข้างต้น โดยเฉพาะสมบัติการสลับที่ สมบัติการเปลี่ยนหมู่ และสมบัติการแจกแจง สามารถช่วยให้น้อง ๆ หาผลลัพธ์จากการบวกและการคูณของจำนวนจริงทำได้สะดวกขึ้นด้วย อย่างเช่นในตัวอย่างต่อไปนี้
- จงหาผลบวกของ 2+5+3+2+8+5
ถ้าเราไม่ใช้สมบัติข้างต้น เราจะต้องดำเนินการบวกจากจำนวนทางซ้ายสุดมาขวาสุด ซึ่งจะไม่สะดวกเลย แต่ถ้าเราใช้สมบัติมาช่วยจะสามารถสลับที่และเพิ่มวงเล็บ(จัดหมู่) จะช่วยให้เราหาผลบวกได้ง่ายขึ้น ดังนี้
2+5+3+2+8+5=(5+5)+(2+8)+(2+3)=10+10+5=25
- จงหาผลคูณของ 2\times 5\times 3\times 2\times 8\times 5
เราสามารถใช้สมบัติการคูณของจำนวนจริงช่วยในการหาคำตอบได้เช่นเดียวกับตัวอย่างก่อนหน้า ดังนี้
2\times 5\times 3\times 2\times 8\times 5 = \left (2\times 5 \right )\times \left (2\times 5 \right )\times \left ( 3\times 8 \right )=10\times 10\times 24=2,400
พหุนามตัวแปรเดียว
ขึ้นหัวข้อมาว่าพหุนาม น้อง ๆ อาจจะงงว่าแล้วมันเกี่ยวกับจำนวนจริงตรงไหนเหรอ ? นั่นเป็นเพราะว่านอกจากการบวกลบคูณหารแล้ว เราใช้สมบัติของจำนวนจริงในการหาคำตอบของสมการและอสมการด้วยนั่นเอง !!
โดยที่แต่เดิมเราเคยแก้สมการและอสมการตัวแปรเดียวที่เป็นแบบเชิงเส้น (ตัวแปรไม่ได้มีเลขชี้กำลัง) กันมาบ้าง แต่ในระดับชั้นนี้ เราจะไปไกลขึ้น โดยตัวแปรของเรานั้นมีเลขชี้กำลังได้ นั่นทำให้สมการหรืออสมการจะอยู่ในรูปของพหุนามนั่นเอง
ในหัวข้อนี้ เราก็จะมาทบทวนพหุนาม เน้นที่พหุนามตัวแปรเดียว แล้วต่อยอดว่าพหุนามสามารถทำอะไรได้มากไปกว่าที่เราเคยเรียนรู้มาในคณิต ม.ต้น ซึ่งความรู้เรื่องพหุนามตัวแปรเดียวในหัวข้อนี้ก็จะนำไปใช้ในการแก้สมการและอสมการต่อนั่นเอง
ความหมายของพหุนาม
p(x)={a_{n}x}^{n}+{a_{n-1}x}^{n-1}+{a_{n-2}x}^{n-2}+\cdots+a_{1}x+a_{0}
เมื่อ n เป็นจำนวนเต็มที่ไม่เป็นจำนวนลบ
และ {a_{n}}, {a_{n-1}}, {a_{n-2}}, … , {a_{1}}, {a_{0}} เป็นจำนวนจริง
เรียก p(x) ว่า พหุนามดีกรี n เรียก n ว่า
ดีกรี ของ p(x) และเรียก {a_{n}}, {a_{n-1}}, {a_{n-2}}, … , {a_{1}}, {a_{0}} ว่า สัมประสิทธิ์ ของ p(x)
เรียก {a_{n}} ว่า สัมประสิทธิ์นำ
เช่น q(x)={{3x}^{2}}+{4x}+5 เป็นพหุนามที่มีดีกรี 2 มีสัมประสิทธิ์ เป็น 3, 4 และ 5
และมี สัมประสิทธิ์นำ เป็น 3
การดำเนินการของพหุนาม
ในส่วนของการดำเนินการของพหุนาม ซึ่งประกอบด้วย การบวก ลบ คูณ หารพหุนาม พี่จะขอทบทวนส่วนที่เราเคยเรียนในชั้น ม.ต้นกันก่อน ได้แก่ การบวก ลบ และคูณพหุนาม ซึ่งเรามาทบทวนผ่านตัวอย่างต่อไปนี้กันเลย
ตัวอย่างที่ 1
ให้ p(x)=x-2 และ q(x)=2x-1 จงหา p(x)+q(x), p(x)-q(x) และ p(x) q(x)
วิธีทำ จาก p(x)=x-2 และ q(x)=2x-1
จะได้
- p(x)+q(x)=(x-2)+(2x-1)=x+2x-2-1=3x-3
- p(x)-q(x)=(x-2)-(2x-1)=x-2x-2+1=-x-2
- p(x)q(x)=(x-2)(2x-1)
=x(2x)+(x)(-1)+(-2)(2x)+(-2)(-1)
=2x^{2}-5x+2
ขั้นตอนวิธีการหารสำหรับพหุนาม
หลังจากที่เราได้ทบทวนการบวก ลบ และคูณพหุนามแล้ว คราวนี้เรามาทำความรู้จักกับการหารพหุนามกันบ้างว่ามีวิธีทำอย่างไร แต่ก่อนอื่น พี่จะพาน้อง ๆ มารู้จักกับองค์ประกอบต่าง ๆ ที่เกี่ยวข้องกับการหารพหุนามว่ามีอะไรบ้าง
ทฤษฎีบท ขั้นตอนวิธีการหารสำหรับพหุนาม
ถ้าหารพหุนาม p(x) ด้วยพหุนาม q(x) โดยที่ q(x)\neq 0 แล้วจะมีพหุนาม a(x) และ r(x) เพียงชุดเดียวเท่านั้นซึ่ง
p(x)=q(x)a(x)+r(x)
โดย r(x)=0 หรือ ดีกรีของ r(x) มีค่าน้อยกว่าดีกรีของ a(x)
จากทฤษฎีข้างต้นสรุปง่าย ๆ ว่า
ตัวตั้ง = (ตัวหาร)(ผลหาร) + เศษเหลือ
การหารยาว
การหารพหุนามนั้นมีได้หลายวิธี เช่น วิธีการหารยาว วิธีเทียบสัมประสิทธิ์ วิธีการหารสังเคราะห์ ฯลฯ แต่พี่จะขอพูดถึงเฉพาะการหารยาวนะ ซึ่งการหารยาวของพหุนามสามารถทำได้โดยวิธีการตั้งหารคล้ายรูปแบบการหารยาวของจำนวนเต็มดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 2
จงหาผลหารและเศษเหลือจากการหาร p(x)=x^{2}-3x+2
ด้วย q(x)=x-4
วิธีทำ
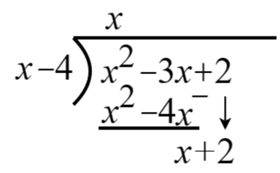
1. จัดตำแหน่งของ ตัวตั้ง และ ตัวหารเหมือนกับการหารยาวของจำนวนเต็ม
โดยเรียงเลขชี้กำลังจากมากไปน้อยทั้งตัวตั้งและตัวหาร
2. หาตัวที่คูณกับ x แล้วได้ x^{2} นั่นก็คือ x
3. หาผลคูณของ x(x-4)
4. เอาผลที่ได้จากข้อที่ 3 ตั้งในบรรทัดถัดไปแล้วนำไปลบออกจาก x^{2}-3x ที่อยู่ด้านบน
5. ดึงพจน์ถัดไปลงมา
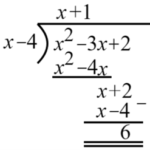
6. หาตัวที่คูณกับx แล้วได้ x นั่นก็คือ 1
7. เอาผลคูณของ (1)(x-4) ตั้งในบรรทัดถัดไปแล้วนำไปลบออกจาก x+2 ที่อยู่ด้านบน จะได้ x^{2}-3x+2=(x-4)(x+1)+6
ดังนั้นผลหารคือ x+1 และเหลือเศษคือ 6
ตัวอย่างที่ 3 จงหาผลหารและเศษเหลือจากการหารพหุนาม 3x^{2}+8 ด้วย x-2
เทคนิค : ในกรณีที่กำลังเรียงพจน์ของพหุนามตามเลขชี้กำลังจากมากไปน้อย แล้วมีพจน์บางพจน์หายไป ให้เติม 0 คูณกับ x ยกกำลังเลขที่หายไป
วิธีทำ
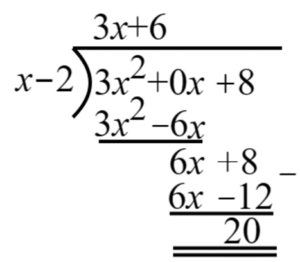
ดังนั้น ผลหารคือ 3x+6 และเหลือเศษคือ 20
การแยกตัวประกอบของพหุนาม
เรื่องหนึ่งที่สำคัญของพหุนาม คือ การแยกตัวประกอบของพหุนาม ซึ่งเป็นส่วนสำคัญทั้งการจัดรูปพหุนามให้อยู่ในรูปอย่างง่าย รวมถึงเป็นวิธีการหลักในการแก้สมการและอสมการพหุนาม
ซึ่งในชั้นม.ต้นน้อง ๆ ได้ทำการแยกตัวประกอบของพหุนามดีกรีสองรวมถึงพหุนามดีกรีสูงกว่าสองที่มีรูปแบบเฉพาะมาแล้ว สำหรับชั้นม.ปลายนี้เนื้อหาที่เราเรียนก็จะเพิ่มขึ้นนะ โดยเราจะได้เรียนการแยกตัวประกอบของพหุนามดีกรีสูงกว่าสองแต่ไม่ได้มีรูปแบบเฉพาะ โดยใช้ทฤษฎีที่สำคัญ อยู่ 2 ทฤษฎี ได้แก่ ทฤษฎีบทเศษเหลือและทฤษฎีบทตัวประกอบตรรกยะ
ทฤษฎีบทเศษเหลือ
ถ้าหารพหุนาม p(x) ด้วยพหุนาม x-c แล้วเศษเหลือจะเท่ากับ p(c)
ตัวอย่างที่ 4 จงหาเศษเหลือของ 3x^{2}+1 หารด้วย x-1
วิธีทำ
ให้ p(x)=3x^{2}+1
จากทฤษฎีบทเศษเหลือ เมื่อหาร p(x) ด้วย x-1 จะได้เศษเหลือคือ p(1)
จะได้ p(1)=3(1)^{2}+1=4
ดังนั้น เศษเหลือของ 3x^{2}+1 หารด้วย x-1 คือ 4
จาก ทฤษฎีบทเศษเหลือ ถ้าเราหาค่า c ที่ทำให้ p(c) เป็น 0 นั่นคือการหารนั้นจะมีเศษเหลือจากการหารเป็น 0 ซึ่งการที่เศษเป็น 0 ก็คือการหารลงตัวนั่นเอง ซึ่งถ้าหารลงตัวแล้วแสดงว่า x-c ก็จะเป็นหนึ่งในตัวประกอบของ p(x) เราสามารถกล่าวเป็นทฤษฎีบทได้ดังนี้
ทฤษฎีบทตัวประกอบ
พหุนาม p(x) มีพหุนาม x-c เป็นตัวประกอบก็ต่อเมื่อ p(c)=0
ตัวอย่างที่ 5 จงตรวจสอบว่า x-1 เป็นตัวประกอบของ x^{2}+2x-8 หรือไม่
วิธีทำ
ให้ p(x)=x^{2}+2x-8
ดังนั้น p(1)=(1)^{2}+2(1)-8=-5 ซึ่งไม่เท่ากับ 0
จึงสรุปได้ว่า x-1 ไม่เป็นตัวประกอบของ x^{2}+2x-8
ทฤษฎีบทตัวประกอบตรรกยะ
ให้ p(x) แทนพหุนาม {a_{n}x}^{n}+{a_{n-1}x}^{n-1}+{a_{n-2}x}^{n-2}+…+a_{1}x+a_{0}
โดยที่ {a_{n}}, {a_{n-1}}, {a_{n-2}}, … , {a_{1}}, {a_{0}} เป็นจำนวนเต็ม
ซึ่ง {a_{n}}\neq 0
ถ้า x-\frac{k}{m} เป็นตัวประกอบของพหุนาม p(x) โดยที่ m และ k เป็นจำนวนเต็ม
ซึ่ง {m}\neq 0 และ ห.ร.ม. ของ m และ k
เท่ากับ 1 แล้ว m หาร a_{n} ลงตัว และ k หาร a_{0} ลงตัว
ตัวอย่างที่ 6 จงแยกตัวประกอบของ 2x^{2} + x^{5} – 3
วิธีทำ
ให้ p(x) = 2x^{2} + 5x -3
เนื่องจากจำนวนเต็มที่หาร -3 ลงตัว คือ \pm 1, \pm 3
และจำนวนเต็มที่หาร 2 ลงตัว คือ \pm 1, \pm 2
ดังนั้น จำนวนตรรกยะ \frac{k}{m} ที่ทำให้ p\left ( \frac{k}{m} \right )=0 จะอยู่ในกลุ่มของจำนวนต่อไปนี้ คือ \pm 1, \pm 3, \pm \frac{1}{2}, \pm \frac{3}{2}
พิจารณา p\binom{1}{2}
จะได้ว่า p\binom{1}{2} = 2\binom{1}{2}^{2} + 5\binom{1}{2} – 3 = \frac{1}{2} + \frac{5}{2} -3 = 0
นั่นคือ x-\frac{1}{2} เป็นตัวประกอบของ p(x)
นำ x-\frac{1}{2} ไปหาร p(x) ได้ผลหารเป็น 2x + 6
ดังนั้น 2x^{3} + 5x – 3 = \left ( x-\frac{1}{2} \right ) (2x + 6)
= \left ( x-\frac{1}{2} \right ) (2)(x + 3)
= (2x – 1) (x + 3)
จากตัวอย่างข้างต้น น้อง ๆ บางคนที่ยังสงสัยอยู่ว่า จำนวน \pm 1, \pm 3, \pm \frac{1}{2}, \pm \frac{3}{2} เหล่านี้มาจากไหน พี่จะขอสรุปไว้ข้างท้ายนี้อีกครั้งว่า ตัวเศษได้มาจากตัวประกอบของ -3 และตัวส่วนได้มาจากตัวประกอบของ 2 โดย ห.ร.ม. ของตัวเศษและตัวส่วน คือ 1 นั่นเอง
สมการพหุนาม
คราวนี้ก็มาถึงเวลาที่เราจะนำความรู้ทั้งจำนวนจริงและพหุนามมาใช้ในการแก้สมการกันแล้ว เราเคยผ่านการแก้สมการมาตั้งแต่ชั้นประถม และในม.ต้นเราได้แก้สมการกำลังสองด้วย ในม.ปลายเราจะแก้สมการที่ตัวแปรมีเลขชี้กำลังที่มากขึ้น แต่เราจะใช้หลักการแก้สมการกำลังสองร่วมกับทฤษฎีบทตัวประกอบในหัวข้อก่อน สำหรับหลักการแก้สมการพหุนาม (ทั้งกำลังสองและกำลังที่สูงกว่าสอง) วิธีหลัก ๆ ที่นิยมใช้กันคือวิธีการแยกตัวประกอบ และอีกวิธีคือการใช้สูตร
ตัวอย่างที่ 7 จงหาค่าของ x เมื่อ x^{2}+3x-54=0
วิธีทำ
ทำการแยกตัวประกอบพหุนาม
x^{2}+3x-54 =0
(x-6)(x+9) =0
จะได้ x-6=0 หรือ x+9=0
ดังนั้น x=6, -9
ตัวอย่างข้างต้นคือวิธีการแยกตัวประกอบ ส่วนการใช้สูตรจะมีสูตรและตัวอย่างการใช้ดังนี้
ตัวอย่างที่ 8 จงหาเซตคำตอบของสมการ x^{2}-6x+9=0
วิธีทำ
จากสูตร เทียบสัมประสิทธิ์ ax^{2}+bx+c=0 กับ x^{2}-6x+9=0
จะได้ a=1, b=-6 และ c=9
ซึ่ง (-6)^2-4(1)(9)=0 ดังนั้นสมการพหุนามนี้มีเพียงคำตอบเดียวนั่นคือ
x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}
=\frac{-(-6)\pm \sqrt{0}}{2(1)}=3
ดังนั้น x=3
จะได้เซตคำตอบของสมการนี้คือ \left \{ 3 \right \}
ตัวอย่างที่ 9 จงหาเซตคำตอบของสมการ 2x^{2}+3x+4=0
วิธีทำ
จากสูตร เทียบสัมประสิทธิ์ ax^{2}+bx+c=0 กับ 2x^{2}+3x+4=0
จะได้ a=2, b=3 และ c=4
ซึ่ง (3)^2-4(2)(4)<0 ดังนั้นสมการพหุนามนี้ไม่มีจำนวนจริงที่เป็นคำตอบ
ดังนั้น เซตคำตอบของสมการนี้คือ เซตว่าง นั่นเอง
เศษส่วนของพหุนาม
ก่อนอื่น เรามารู้จักกับกับ เศษส่วนของพหุนามกันว่าคืออะไร
บทนิยาม ให้ p(x) และ q(x) พหุนาม โดยที่ q(x)\neq 0 จะเรียก \frac{p(x)}{q(x)} ว่า เศษส่วนพหุนาม ที่มี p(x) เป็นตัวเศษ และ q(x) เป็นตัวส่วน |
จากบทนิยาม เศษส่วนของพหุนามก็คือ เศษส่วนที่มีตัวเศษและตัวส่วนเป็นพหุนามนั่นเอง เหมือนเอาเศษส่วนและพหุนามมารวมตัวกัน ดังนั้น เศษส่วนของพหุนามก็จะสามารถใช้สมบัติต่าง ๆ ของเศษส่วน และสมบัติต่าง ๆ ของพหุนามมาใช้ในการคำนวณ จัดรูป รวมถึงนำไปใช้แก้สมการและอสมการได้นะ
การดำเนินการของเศษส่วนพหุนาม
การดำเนินการของเศษส่วนพหุนามนั้นมีวิธีทำคล้ายคลึงกับการดำเนินการของเศษส่วนจำนวนเต็ม คือมีวิธีการบวก ลบ คูณ และหารเหมือนเศษส่วนที่เราเคยรู้จัก แล้วบางข้ออาจใช้การแยกตัวประกอบของพหุนามในการจัดรูปร่วมด้วย ตามตัวอย่างด้านล่างนี้เลย
ตัวอย่างที่ 10
กำหนดให้ p(x)=\frac{x+4}{2} และ q(x)=\frac{1}{x+3}
จงหา p(x)+q(x), p(x)-q(x), p(x) q(x) และ \frac{p(x)}{q(x)}
วิธีทำ
จาก p(x)=\frac{x+4}{2} และ q(x)=\frac{1}{x+3}
จะได้ p(x)+q(x)=\frac{x+4}{2}+\frac{1}{x+3}
=\frac{(x+4)(x+3)+(2)(1)}{(2)(x+3)}
=\frac{x^{2}+7x+14}{2x+6}
p(x)-q(x)=\frac{x+4}{2}-\frac{1}{x+3}
=\frac{(x+4)(x+3)-(2)(1)}{(2)(x+3)}
=\frac{x^{2}+7x+10}{2x+6}
p(x)q(x)=\left ( \frac{x+4}{2}\right )\left ( \frac{1}{x+3} \right )
=\frac{(x+4)(1)}{(2)(x+3)}
=\frac{x+4}{2x+6}
\frac{p(x)}{q(x)}=\left ( \frac{x+4}{2}\right )\div \left ( \frac{1}{x+3} \right )
=\left ( \frac{x+4}{2} \right )\left ( \frac{x+3}{1} \right )
=\frac{x^{2}+7x+12}{2}
สมการเศษส่วนพหุนาม
เนื้อหาก่อนหน้านี้เราทราบกันแล้วว่าจะสามารถแก้สมการพหุนามได้อย่างไร สำหรับการแก้สมการเศษส่วนพหุนามนั้นใช้หลักการแก้สมการพหุนามเหมือนเดิม เพิ่มเติมคือตัวส่วนต้องไม่เป็น 0 น้าา
ตัวอย่างที่ 11 จงหาเซตคำตอบของสมการ \frac{x^{2}+7x+12}{x^{2}+3x-4}=0
วิธีทำ
จาก \frac{x^{2}+7x+12}{x^{2}+3x-4}=0
จะได้ \frac{(x+4)(x+3)}{(x+4)(x-1)}=0
จะได้ (x+4)(x+3)=0 และ (x+4)(x-1)\neq 0
นั่นคือ x=-3 หรือ x=-4 โดยที่ x\neq 1 และ x\neq -4
ดังนั้น x=-3
จะได้เซตคำตอบของสมการคือ \left \{ -3 \right \}
มาสรุปแนวคิดการแก้ปัญหาในตัวอย่างข้างต้นกันอีกครั้งน้าา เราจะเเยกตัวประกอบแล้วหาค่า x แต่ละตัวแล้วดูเงื่อนไขว่า x ไม่สามารถเป็นอะไรได้ และตัดคำตอบที่ทำให้ตัวส่วนเป็น 0 ทิ้ง
การไม่เท่ากันของจำนวนจริง
น้อง ๆ จำเรื่องสัจพจน์การเท่ากันของจำนวนจริงที่พี่อธิบายก่อนหน้านี้กันได้มั้ย คราวนี้พี่จะมาพูดส่วนของ “การไม่เท่ากัน” บ้าง โดยในส่วนนี้จะมีความสัมพันธ์อื่น ๆ ที่น้อง ๆ ต้องรู้จักเพิ่มนอกจากเท่ากับ ได้แก่ มากกว่า “>” น้อยกว่า “<” มากกว่าหรือเท่ากับ “\geq” น้อยกว่าหรือเท่ากับ “\leq” นั่นเอง
ในส่วนของสัจพจน์เชิงคณิตศาสตร์ของระบบจำนวนจริงเกี่ยวกับ “การเท่ากัน”เราได้กล่าวไปแล้ว ในหัวข้อนี้เราจะลองพูดถึงสัจพจน์ของการไม่เท่ากันของระบบจำนวนจริงดูบ้าง ซึ่งจะมีอยู่ 3 ข้อ ตามนี้เลย
สำหรับ a\in \mathbb{R} และ b\in \mathbb{R}
1. ถ้า a>0 และ b>0 แล้ว a+b>0
(จำนวนจริงบวก 2 ตัวบวกกันจะได้จำนวนจริงบวก)
2. ถ้า a>0 และ b>0 แล้ว ab>0
(จำนวนจริงบวก 2 ตัวคูณกันจะได้จำนวนจริงบวก)
3. a=0 หรือ a>0 หรือ a<0 เพียงอย่างใดอย่างหนึ่ง
(จำนวนจริงไม่สามารถมีค่าเป็นบวก ลบ หรือ 0 พร้อมกันได้)
ถ้า a\in \mathbb{R}^{+} แสดงว่า a เป็นจำนวนจริงบวก หรือหมายความได้ว่า a>0 นั่นเอง เราลองมาดูบทนิยามที่เกี่ยวกับการไม่เท่ากันของจำนวนจริงกันดีกว่า
บทนิยาม
ให้ a และ b เป็นจำนวนจริง
- a > b หมายถึง a – b > 0
- a < b หมายถึง a-b < 0 (หรือ b – a > 0)
- a \geq b หมายถึง a > b หรือ a = b
- a \leq b หมายถึง a < b หรือ a = b
จากบทนิยามที่ได้กล่าวมาอาจจะยังนำไปใช้ประโยชน์โดยตรงได้ไม่เยอะมากนัก นักคณิตศาสตร์เลยนำบทนิยามดังกล่าวไปต่อยอดมาเป็นทฤษฎีบทให้เราสามารถใช้ได้อีกมากมายเลย เราลองไปดูทฤษฎีบทที่สำคัญ ๆ ของเรื่องนี้กัน
ทฤษฎีบท
ให้ a, b และ c เป็นจำนวนจริง
สมบัติการถ่ายทอด
ถ้า a > b และ b > c แล้ว a > c
สมบัติการบวกด้วยจำนวนที่เท่ากัน
ถ้า a > b แล้ว a+c > b+c
สมบัติการคูณด้วยจำนวนที่เท่ากันที่ไม่เป็นศูนย์
กรณีที่ 1: ถ้า a > b และ c > 0 แล้ว ac > bc
กรณีที่ 2: ถ้า a > b และ c < 0 แล้ว ac < bc
สมบัติการตัดออกสำหรับการบวก
ถ้า a+c > b+c แล้ว a > b
สมบัติการตัดออกสำหรับการคูณ
กรณีที่ 1: ถ้า ac > bc และ c > 0 แล้ว a > b
กรณีที่ 2: ถ้า ac > bc และ c < 0 แล้ว a < b
จากทฤษฎีบทข้างบนนี้ สิ่งที่น้องต้องระวังเป็นพิเศษเลยก็คือ หลังจากคูณหรือหารด้วยจำนวนจริงลบตลอดทั้งอสมการแล้ว อย่าลืมกลับเครื่องหมายอสมการด้วย !!
ทฤษฎีบท
ให้ a, b, c และ d เป็นจำนวนจริง
ถ้า a > b และ c > d แล้ว a+c > b+d
แสดงว่า ถ้าเราสามารถนำสองอสมการมาบวกกันได้เลยตามทฤษฎีบท ยกตัวอย่างเช่น ถ้า x > 5 และ y > 2 จะได้ว่า x+y > 7 นั่นเอง
บทนิยาม
ให้ a, b และ c เป็นจำนวนจริงใด ๆ
a < b < c หมายถึง a < b และ b < c
a \leq b \leq c หมายถึง a \leq b และ b \leq c
a < b \leq c หมายถึง a < b และ b \leq c
a \leq b < c หมายถึง a \leq b และ b < c
อสมการพหุนามตัวแปรเดียว
ก่อนที่น้อง ๆ จะรู้จักเรื่องนี้ พี่ขออธิบายเรื่องหนึ่งซึ่งเป็นเรื่องที่สำคัญมาก ๆ ถ้าไม่เข้าใจเรื่องนี้ น้องจะเข้าใจเรื่องอสมการพหุนามตัวแปรเดียวได้ยากมาก หรืออาจจะไม่เข้าใจเลย (พี่เตือนน้องแล้วนะ) ซึ่งนั่นก็คือเรื่อง “ช่วง” หมายถึง สับเซตของเซตจำนวนจริง โดยมีบทนิยามดังนี้
บทนิยาม ให้ a และ b เป็นจำนวนจริง ซึ่ง a < b
|
หมายเหตุ : เซตของจำนวนจริงสามารถเขียนในรูปช่วง (-\infty, \infty) แทนได้นะ
การเขียนช่วง
จากสัญลักษณ์ของช่วงต่าง ๆ ตามนิยามข้างต้น เราสามารถเขียนแทนจำนวนลงบนเส้นจำนวนได้ตามตัวอย่างตามนี้เลย
ตัวอย่างที่ 12
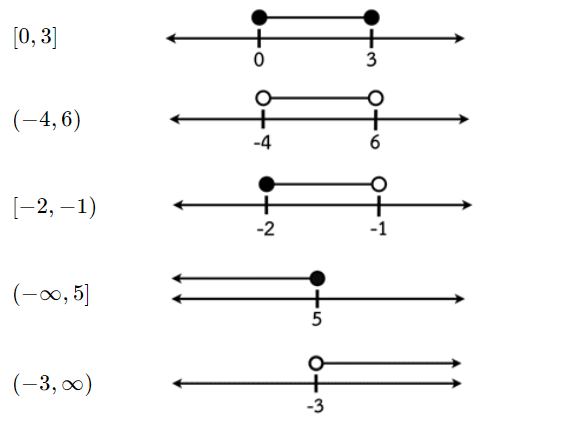
อสมการพหุนามตัวแปรเดียว
อสมการ คือประโยคในทางคณิตศาสตร์ที่กล่าวถึงการไม่เท่ากัน เช่น 10 > 8 คืออสมการที่เป็นจริง หรือ -10\leq -20 คืออสมการที่เป็นเท็จ เป็นต้น แต่ในกรณีที่อสมการมีตัวแปรอยู่ด้วย เช่น 3x+2 > 8 หรือ x^{2}-9\leq 0 เราจะมาหาว่า จำนวนจริงตัวไหนบ้างนะที่แทนลงในอสมการนี้แล้ว ทำให้อสมการเป็นจริง โดยจำนวนจริงเหล่านี้เราจะเขียนในรูปของ “เซตคำตอบของอสมการ”
ตัวอย่างที่ 13
จงหาเซตคำตอบของอสมการ x^{2}+2x-48<0
วิธีทำ
จาก x^{2}+2x-48 <0
แยกตัวประกอบได้ (x+8)(x-6) < 0
สามารถเขียนช่วงคำตอบของ (x+8)(x-6) < 0 ได้ดังนี้
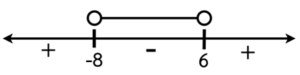
ดังนั้น เซตคำตอบของอสมการ x^{2}+2x-48<0 คือช่วง \left ( -8,6 \right ) หรือ \begin{Bmatrix}x|\, -8<x<6\end{Bmatrix}
ตัวอย่างที่ 14 จงหาเซตคำตอบของอสมการ \frac{(x + 4)(2x – 5)(7 – x)}{x}\geq 0
วิธีทำ
จาก \frac{(x + 4)(2x – 5)(7 – x)}{x}\geq 0
คูณด้วย -1 ตลอด \frac{(x + 4)(2x – 5)(x – 7)}{x}\leq 0 ** คูณด้วยตัวติดลบอย่าลืมกลับเครื่องหมายอสมการ
สามารถเขียนช่วงคำตอบของ \frac{(x + 4)(2x – 5)(x – 7)}{x}\leq 0 ได้ดังนี้
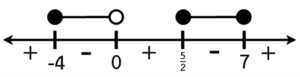
ดังนั้น เซตคำตอบของอสมการ \frac{(x + 4)(2x – 5)(7 – x)}{x}\geq 0 คือช่วง [-4, 0) \cup \left [ \frac{5}{2}, 7 \right ]
ค่าสัมบูรณ์
ยังจำกันได้หรือไม่ สัญลักษณ์อะไรเอ่ยที่เอามาครอบจำนวนต่าง ๆ แล้วค่าที่ได้จะออกมาเป็นบวกเสมอ (ให้เวลาคิด 3 วินาที 3…2…1 หมดเวลา !!!) ถูกต้องแล้ว มันก็คือ “ค่าสัมบูรณ์” นั่นเอง ! ^_^
หลาย ๆ คนน่าจะเคยได้ยินคำว่า “ค่าสัมบูรณ์” มาจากสมัย ม.ต้น ที่ได้เรียนเรื่องจำนวนเต็มมาแล้วไม่มากก็น้อย เดี๋ยวเราจะมาดูกันดีกว่าว่า ค่าสัมบูรณ์ของจำนวนจริง จะถูกนิยามว่าอย่างไร
หมายเหตุ
1. จากบทนิยาม ในกรณีที่ a<0 (a เป็นจำนวนลบ) จะได้ -a>0 (ค่าลบของจำนวนลบจะได้จำนวนบวก) แสดงว่า \left | a \right |=-a ซึ่งเป็นจำนวนเต็มบวก ดังนั้น สำหรับจำนวนจริง a จะได้ว่า \left | a \right | มากกว่าหรือเท่ากับศูนย์ โดย \left | a \right | จะเท่ากับ 0 เมื่อ a=0
2. ค่าสัมบูรณ์ของจำนวนจริง a สามารถพิจารณาเป็นระยะจากจุดที่แทน 0 ถึงจุดที่แทน a บนเส้นจำนวน
ทฤษฎีบท
ให้ x และ y เป็นจำนวนจริง จะได้ว่า
- \left | x \right |=\left | -x \right |
- \left | xy \right |=\left | x \right |\left | y\right |
- \left | \frac{x}{y} \right |=\frac{\left | x \right |}{\left | y\right |}
- \left | x-y \right |=\left | y-x \right |
- \left | x\right |^2=x^2
- \left | x+y\right |\leq \left | x \right |+\left | y \right |
สมการค่าสัมบูรณ์ของพหุนามตัวแปรเดียว
ในหัวข้อนี้เราจะมาแก้สมการค่าสัมบูรณ์ของพหุนามกัน น้อง ๆ น่าจะเคยมีประสบการณ์ในการแก้สมการมาในหลายรูปแบบแล้ว เช่น สมการเส้นตรง สมการกำลังสองตัวแปรเดียว ซึ่งวิธีหนึ่งที่ใช้ในการหาคำตอบของสมการได้ก็คือการแทนค่าหรือจำนวนลงในตัวแปรแล้วทำให้สมการเป็นจริง
น้อง ๆ คิดว่า ถ้าเราต้องการหาคำตอบของสมการค่าสัมบูรณ์ จะต้องมีหลักการอย่างไรดี ลองดูสมการง่าย ๆ เช่น \left | x \right |= 3 ถ้าเราลองแทนค่า x ด้วย 3 สมการนี้จะเป็นจริง ถ้าเราลองแทนค่า x ด้วย -3 สมการนี้ก็ยังเป็นจริงอยู่เช่นกัน แต่ถ้าลองแทนค่า x ด้วยจำนวนอื่น ๆ จะได้ว่าไม่มีจำนวนใดเลยนอกจากนี้ที่ทำให้สมการเป็นจริง ดังนั้น คำตอบทั้งหมดของสมการ \left | x \right |= 3 คือ 3 และ -3 นั่นเอง
ทฤษฎีบท
ให้ a เป็นจำนวนจริงบวก
เซตคำตอบของสมการ \left | x \right |=a คือ \left \{ -a,a \right \}
หรือสรุปง่าย ๆ ได้ว่า \left | x \right |=a ก็ต่อเมื่อ x=a หรือ x=-a นั่นเอง เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราลองมาดูตัวอย่างกัน
ตัวอย่างที่ 15
จงหาเซตคำตอบของสมการ \left | 2x+3 \right |=9
วิธีทำ
จากทฤษฎีบท จะได้ว่า 2x+3=9 หรือ 2x+3=–9
2x=6 หรือ 2x=-12
x=3 หรือ x=-6
ดังนั้น เซตคำตอบของสมการ \left | 2x+3 \right |=9 คือ \left \{-6,3 \right \}
จากตัวอย่างด้านบน แค่น้อง ๆ พิจารณาที่ x=a และ x=-a ก็จะได้คำตอบเลย แต่ถ้าในกรณีที่นอกเครื่องหมายค่าสัมบูรณ์ติดตัวแปร เราไม่แน่ใจว่าจะนอกเครื่องหมายค่าสัมบูรณ์จะมีค่าเป็นบวก หรือมีค่าเป็นลบ เราจึงต้องพิจารณาทุกกรณีในการถอดเครื่องหมายค่าสัมบูรณ์ที่จะเป็นไปได้นั่นเอง ลองไปดูในตัวอย่างถัดไปกัน
ตัวอย่างที่ 16
จงหาเซตคำตอบของสมการ \left | x-1\right |=2x-3
แนวคิด เราจะพิจารณาในกรณีที่ x-1\geq 0และ x-1<0
วิธีทำ
กรณีที่ 1
x-1\geq 0 นั่นคือ x\geq 1
จะได้ x-1 = 2x-3
-1+3 = 2x-x
x = 2 ซึ่งเป็นไปตามเงื่อนไข 2\geq 1
นั่นคือ 2 เป็นคำตอบของสมการ
กรณีที่ 2
x-1<0 นั่นคือ x<1
จะได้ -(x-1) = 2x-3
-x+1 = 2x-3
1+3 = 2x+x
4 = 3x
x =\frac{4}{3} ซึ่งขัดแย้งเงื่อนไข x<1
นั่นคือ \frac{4}{3} ไม่ใช่คำตอบของสมการ
ดังนั้น เซตคำตอบของสมการ \left | x-1\right |=2x-3 คือ \left \{ 2 \right \}
จากตัวอย่างนี้น้องๆ จะเห็นว่า หลังจากที่เราได้คำตอบมาแล้ว ก็ยังไม่สามารถตอบได้ทันที เราต้องนำเงื่อนไขที่กำหนดไว้มาพิจารณาร่วมด้วยและในตัวอย่างถัดไปเราจะมาดูสมการค่าสัมบูรณ์ ที่ทั้งสองข้างอยู่ในรูปค่าสัมบูรณ์กันบ้าง
ตัวอย่างที่ 17 จงหาเซตคำตอบของสมการ \left | x-1 \right |=\left | 2x+1 \right |
แนวคิด เราจะใช้วิธียกกำลังสองทั้งสองข้างของสมการมาช่วยแก้กันดีกว่า
วิธีทำ
จาก \left | x-1 \right | = \left | 2x+1 \right |
ยกกำลังสองทั้งสองข้าง \left | x-1 \right |^2 =\left | 2x+1 \right |^2
(x-1)^2-(2x+1)^2 = 0
[(x-1)-(2x+1)][(x-1)+(2x+1)]=0
(-x-2)(3x)=0
จะได้ -x-2=0 หรือ 3x=0
x=-2 หรือ x=0
ตรวจคำตอบ
แทน x=0 ลงในสมการ \left | x-1 \right | = \left | 2x+1 \right |
จะได้ \left | 0-1 \right |=\left | 2(0)+1\right |
\left | -1\right | =\left | 1\right |
1 = 1 เป็นจริง
แทน x=-2 ลงในสมการ \left | x-1 \right | = \left | 2x+1 \right | จะได้
\left | -2-1 \right |=\left | 2(-2)+1\right |
\left |-3\right |=\left |-3\right |
3 = 3 เป็นจริง
ดังนั้น เซตคำตอบของสมการ \left | x-1 \right |= \left | 2x+1 \right | คือ \left\{-2,0\right \}
อสมการค่าสัมบูรณ์ของพหุนามตัวแปรเดียว
เราได้ลองแก้สมการค่าสัมบูรณ์ไปเป็นที่เรียบร้อยแล้ว จะเห็นได้ว่า วิธีการแก้สมการค่าสัมบูรณ์นั่นมีความแตกต่างจากการแก้สมการที่เราเคยเจอมา ที่นี้เราก็จะมาดูกันว่า การแก้อสมการค่าสัมบูรณ์มีความแตกต่างกับการแก้อสมการทั่วไป อย่างไรบ้าง
การแก้อสมการในรูปค่าสัมบูรณ์
ทฤษฎีบท
ให้ a เป็นจำนวนจริงบวก
- \left | x\right |< a ก็ต่อเมื่อ -a<x<a
- \left | x\right |\leq a ก็ต่อเมื่อ -a\leq x\leq a
- \left | x\right |>a ก็ต่อเมื่อ x<-a หรือ x>a
- \left | x\right |\geq a ก็ต่อเมื่อ x\leq -a หรือ x\geq a
เพื่อเพิ่มความเข้าใจในทฤษฎีบท เราลองมาดูตัวอย่างกัน
ตัวอย่างที่ 18
จงหาเซตคำตอบของอสมการ \left | 2x+3 \right |<9
วิธีทำ
จากทฤษฎีบทจะได้ว่า
-9 < 2x+3 < 9
-9-3 < 2x+3-3 < 9-3
-12 < 2x < 6
-6 < x < 3
ดังนั้น เซตคำตอบของอสมการ คือ \left \{ x | -6< x< 3 \right \} หรือ (-6,3)
นอกจากอสมการที่มีจำนวนเต็มแล้ว เราจะมาดูอสมการที่มีพหุนามว่ามีวิธีแก้โจทย์อย่างไร
ตัวอย่างที่ 19
จงหาเซตคำตอบของอสมการ \left | x+1 \right |>x-3
แนวคิด เราจะพิจารณาในกรณีที่ x+1\geq 0 และ x+1<0
วิธีทำ
กรณีที่ 1
x+1\geq 0 นั่นคือ x\geq -1
จะได้ x+1 > x-3
1 > -3
แสดงว่า x สามารถเป็นจำนวนจริงใดก็ได้ หรือ x\in \mathbb{R}\quad
ดังนั้น ค่า x ที่สอดคล้อง คือ x\geq -1 และ x\in \mathbb{R}\quad
นั่นคือ x\geq -1 หรือ\left [ -1,\infty \right )
กรณีที่ 2
x+1<0 นั่นคือ x<-1
จะได้ -(x+1) > x-3
-x-1 > x-3
-2x > -2
x < 1
ดังนั้น ค่า x ที่สอดคล้อง คือ x<-1 และ x<1
นั่นคือ x< -1 หรือ \left ( -\infty ,-1 \right )
ดังนั้น เซตคำตอบของอสมการ คือ \left ( -\infty ,-1 \right )\cup \left [ -1,\infty \right ) หรือ \mathbb{R}
จะเห็นได้ชัดเจนเลยว่า การตรวจคำตอบเป็นสิ่งสำคัญ หลังจากที่เราได้คำตอบมาแล้ว ก็ยังไม่สามารถตอบได้ทันที เราต้องนำเงื่อนไขที่กำหนดไว้มาพิจารณาร่วมด้วยเพื่อเป็นการตรวจสอบความถูกต้องนั่นเอง ในตัวอย่างถัดไปเราจะมาดูอสมการค่าสัมบูรณ์ ที่ทั้งสองข้างของสมการอยู่ในรูปค่าสัมบูรณ์กันว่าทำอย่างไร
ตัวอย่างที่ 20
จงหาเซตคำตอบของอสมการ \left | x \right |> \left | x-1 \right |
แนวคิด เราจะใช้วิธียกกำลังสองทั้งสองข้างของอสมการ เพื่อปลดเครื่องหมายค่าสัมบูรณ์ออกนั่นเอง
วิธีทำ
เนื่องจาก \left | x \right |>0 และ \left | x-1 \right |>0
จะได้ \left | x \right |^2>\left | x-1 \right |^2
x^2>(x-1)^2
x^2>x^2-2x+1
2x>1
x>\frac{1}{2}
ดังนั้น เซตคำตอบของอสมการ คือ\left ( \frac{1}{2} ,\infty \right )
หลังจากได้อ่านสรุปเนื้อหาและฝึกทำแบบฝึกหัดกันไปบางส่วน หลายคนคงจะเข้าใจเนื้อหาบทจำนวนจริงเพิ่มขึ้นแล้ว
ใช่ไหมม แต่ถ้าใครยังไม่เข้าใจก็เป็นไรน้าา พี่อยากให้น้อง ๆ ค่อย ๆ ทำความเข้าใจเนื้อหาและฝึกทำโจทย์กันบ่อย ๆ ควบคู่ไปด้วยกันน้า จะได้ทำโจทย์คล่องมือมากขึ้น แถมเป็นการทบทวนเนื้อหาไปในตัวด้วย ซึ่งถ้าใครกำลังมองหาโจทย์หรือ
แบบฝึกหัดที่อยากฝึกทำเพิ่มเติม พี่ก็มีให้ดาวน์โหลดข้อสอบจำนวนจริง ม.4 ด้วยน้าา แวะไปดูกันได้เลยย
ส่วนน้อง ๆ คนไหนที่ลองทำโจทย์หรือดูคลิปติวแล้วยังไม่เข้าใจ อาจเป็นเพราะยังไม่แม่นเนื้อหา หรือพื้นฐานจากบทเรียนก่อนหน้านี้ไม่แข็งแรง พี่แนะนำให้ทวนเนื้อหาให้แม่นก่อนน้า แล้วค่อยมาทำโจทย์เพื่อทบทวนความเข้าใจของตัวเอง
แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ อยากได้คนช่วยไกด์ พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมาก เพราะแพ็กม.5 – ม.6 เรียนได้ถึง 2 ปี และแพ็ก ม.4 – ม.6 เรียนได้ถึง 3 ปี พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมาก นอกจากนี้ยังพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ และถ้าแพ็กไม่ตรงกับบทที่โรงเรียนสอน น้อง ๆ ก็สามารถเลือกเป็นคอร์สแยกบทได้เพราะมีคอร์สติวแยกบทของคณิต ม.ปลายทุกบทเลย แน่นอนว่ามีส่วนลดพิเศษเช่นกันน้า ใครสนใจ คลิก ไปดูรายละเอียดก่อนได้น้าา
ดูคลิปติวเรื่อง "จำนวนจริง ม.4"
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
บทความ แนะนำ
เซต (Set) คืออะไร สรุปเนื้อหาเซต ม.4 พร้อมโจทย์และเฉลย
ตรรกศาสตร์ ม.4 สรุปครบทุกเนื้อหาพร้อมโจทย์ตรรกศาสตร์และวิธีทำ - SmartMathPro
คณิตศาสตร์ ม.4 เทอม 1,2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
คณิตศาสตร์ ม.5 เทอม 1 เทอม 2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
บทความ แนะนำ
คณิตศาสตร์ ม.4 เทอม 1, ม.4 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
