มีใครรู้บ้างมั้ยว่า บทเซตที่เป็นเนื้อหาแรกของคณิตม.4 ถ้าอิงเนื้อหาตามหลักสูตร สสวท. เนี่ย เป็นพื้นฐานให้กับหลายบทในคณิตม.ปลาย เลยน้า ซึ่งพี่แนะนำว่าน้อง ๆ ม.4 ควรจะต้องเก็บพื้นฐานเรื่องนี้ให้แม่น เพื่อที่จะต่อยอดในบทอื่นได้ แต่ถ้าใครลองอ่านจากเนื้อหาในบทเรียนแล้วยังไม่เข้าใจ ก็ไม่ต้องกังวลไป
เพราะวันนี้พี่สรุปเนื้อหาพื้นฐานพร้อมตัวอย่างโจทย์และคลิปติวเพื่อให้น้อง ๆ ได้เข้าใจเนื้อหามากขึ้น ที่สำคัญ คือ ท้ายบทความพี่มีแจกเช็กลิสต์จุดระวังพลาดสำหรับเรื่องเซตให้ด้วยน้าาา ถ้าใครพร้อมแล้ว ไปดูกันเลยย > <
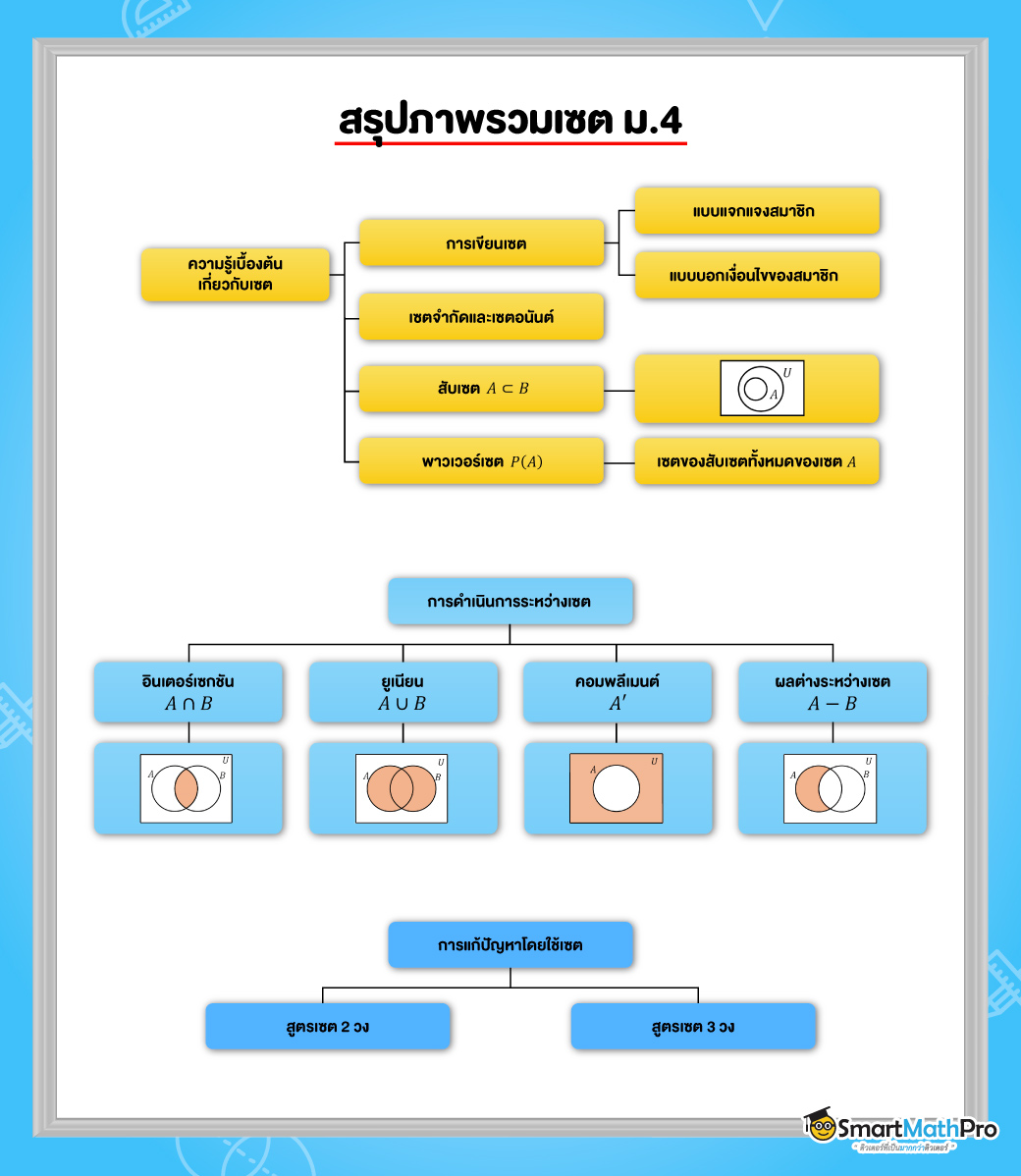
เซต (Set) คืออะไร ?
เซต คือ กลุ่มของสิ่งต่าง ๆ ที่สนใจ โดยเมื่อกล่าวถึงกลุ่มใดจะสามารถบอกได้แน่นอน ว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่ม มักใช้อักษรภาษาอังกฤษตัวใหญ่ในการกล่าวถึงเซต เช่น กลุ่มของประเทศในเอเชีย
- ตัวอย่างเซต เช่น เซตของประเทศในเอเชียตะวันออกเฉียงใต้
- ตัวอย่างของสิ่งที่ไม่ใช่เซต เช่น เซตของคนหน้าตาดี (เพราะไม่สามารถบอกได้แน่ชัดว่าแต่ละคนอยู่หรือไม่อยู่ในกลุ่มนี้)
สมาชิก คือ สิ่งที่อยู่ในเซต โดยใช้สัญลักษณ์ ∈ แทนคำว่า “เป็นสมาชิก” หรือ “อยู่ใน” เช่น ถ้า 7 เป็นสมาชิกของเซต A จะเขียนแทนด้วยสัญลักษณ์ 7 ∈ A
วิธีการเขียนเซตรูปแบบต่าง ๆ
การเขียนเซต เราจะสามารถเขียนได้ 2 รูปแบบ ได้แก่
- แบบแจกแจงสมาชิก เขียนสมาชิกทุกตัวของเซต โดยใช้ { } ครอบสมาชิกของเซตทั้งหมด และใช้สัญลักษณ์ , เพื่อแยกสมาชิกแต่ละตัว เช่น {ม่วง, คราม, น้ำเงิน, เขียว, เหลือง, แสด, แดง}
- แบบบอกเงื่อนไขของสมาชิก ใช้ตัวแปรแทนสมาชิกแล้วบรรยายสมบัติหรือเงื่อนไข เช่น { x | x คือสีที่เป็น
องค์ประกอบของสีรุ้ง}
เซตมีกี่ชนิด ?
เซตจะถูกแบ่งเป็น 2 ชนิด คือ เซตจำกัดและเซตอนันต์ โดยจะมีความแตกต่างกัน ดังนี้
เซตจำกัด
เซตที่มีจำนวนสมาชิกเป็นศูนย์หรือจำนวนเต็มบวก (บอกจำนวนได้) เช่น A = {1, 2, 3, 4} ก็คือ เซต A มีสมาชิกทั้งหมด 4 ตัว นั้นก็คือบอกจำนวนได้ จึงเป็นเซตจำกัด
เซตอนันต์
เซตอนันต์ จะตรงข้ามกับ เซตจำกัด หรือเรียกว่า เป็นเซตที่ไม่ใช่เซตจำกัด มีจำนวนสมาชิกมากมายนับไม่ถ้วน เราจะไม่สามารถระบุจำนวนของสมาชิกได้ เช่น Q = {1, 2, 3, …} จะเห็นว่า เซต Q เราไม่สามารถระบุได้ว่า สมาชิกตัวสุดท้ายคืออะไร และมีจำนวนสมาชิกทั้งหมดเท่าไหร่ นั่นทำให้ เซต Q เป็นเซตอนันต์นั่นเอง
จำนวนสมาชิกของเซต
ใช้สัญลักษณ์ n(A) แทนจำนวนสมาชิกของเซตจำกัด A
ถ้า A = {1, b, ขนมปัง} จะได้ว่า n(A) = 3 หากในเซตมีสมาชิกซ้ำกัน จะนับสมาชิกที่ซ้ำรวมเป็นตัวเดียว
เซตว่าง
คือ เซต ที่ไม่มีสมาชิก โดยใช้สัญลักษณ์ { } หรือ \varnothing แทนเซตว่าง เช่น เซตของจำนวนเต็มบวกที่มีค่าน้อยกว่า 0
เอกภพสัมพัทธ์
ในการเขียนเซตจะต้องกำหนดเขตที่บ่งบอกถึงขอบเขตของสิ่งที่จะพิจารณา เรียกเซตกำหนดเขตนี้ว่า เอกภพสัมพัทธ์ (Relative Universe) ซึ่งมักเขียนแทนด้วย U
สำหรับเอกภพสัมพัทธ์ที่พบบ่อย เช่น
ℕ คือ เซต ของจำนวนนับ หรือ จำนวนเต็มบวก
ℤ คือ เซตของจำนวนเต็ม
ℝ คือ เซตของจำนวนจริง
เซตที่เท่ากัน
เซต A = B หมายความว่า เซต A และเซต B มีสมาชิกทุกตัวในเซตทั้งสองเหมือนกัน
สับเซต
เซต A เป็นสับเซตของ B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของ B เขียนแทนด้วยสัญลักษณ์ A ⊂ B
ตัวอย่างที่ 1
ให้ A = {1, a } จะได้ว่า สับเซตทั้งหมดของ A คือ \varnothing, {1}, { a }, {1, a }
โดยมีสมบัติของสับเซตที่น่าสนใจคือ
- \varnothing เป็นสับเซตของทุกเซต
- A เป็นสับเซตของ A
- ถ้าเซต A มีสมาชิก n ตัว จะได้ว่า A มีสับเซตทั้งหมด 2^n ตัว
เพาเวอร์เซต
เรียกเซตของสับเซตทั้งหมดของเซต A ว่า เพาเวอร์เซต (Power Set) ของเซต A เขียนแทนด้วย P(A)
ตัวอย่างที่ 2
ให้ A = {1, a } จะได้ว่า P(A) = { \varnothing, {1}, {a}, {1, a}}
แผนภาพเวนน์
แผนภาพเวนน์เป็นการแสดงเซตเป็นภาพ ซึ่งช่วยให้เห็นภาพความสัมพันธ์ระหว่างเซต และใช้การแก้ปัญหาเรื่องเซต
ได้ง่ายขึ้น
ตัวอย่างที่ 3
ให้ 𝒰 = {1, 2, 3, 4, 5, 6}, A = {1, 5, 6}, B = {2, 4, 6} สามารถเขียนเป็นแผนภาพเวนน์ ดังรูป
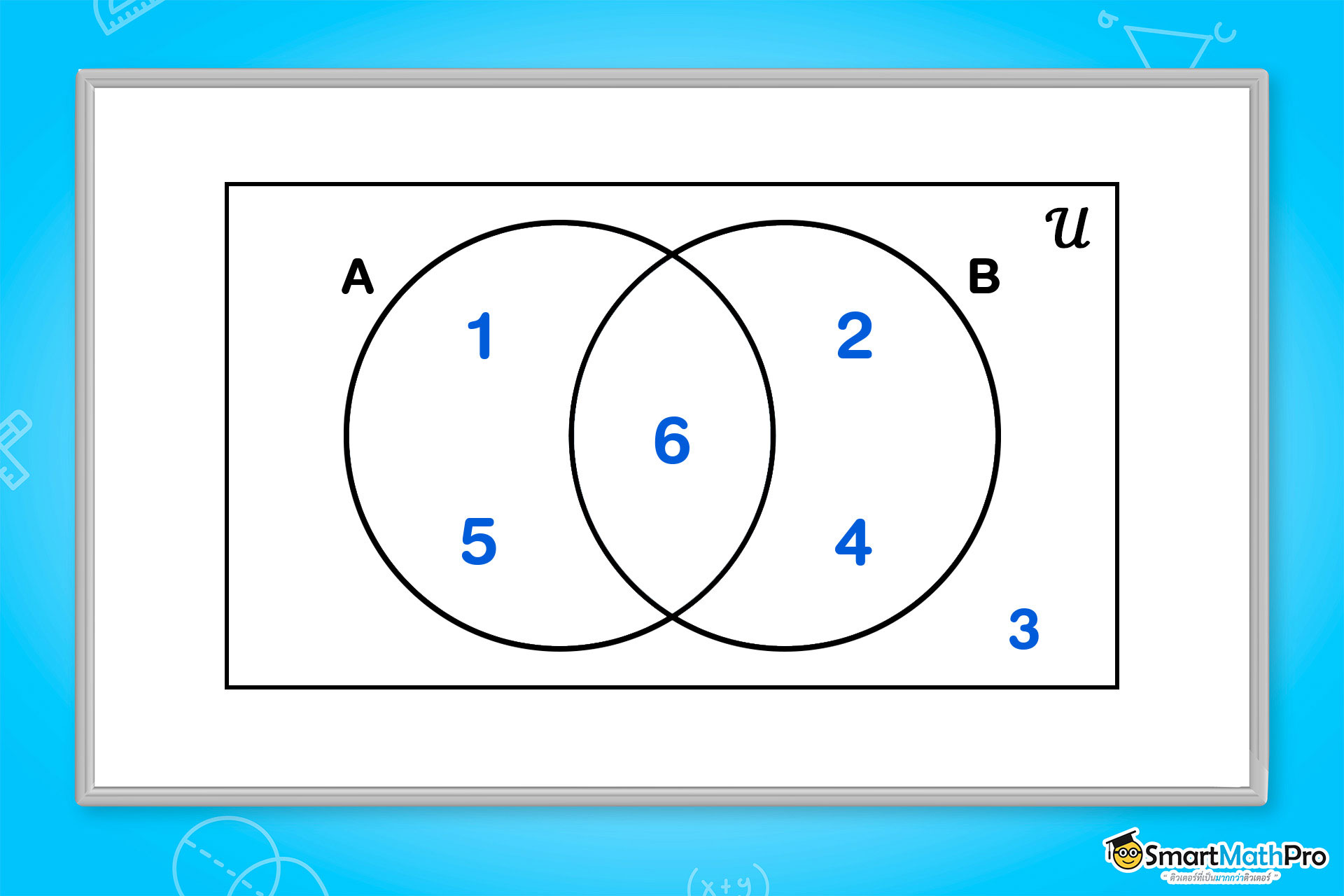
การดำเนินการของเซต
- อินเตอร์เซกชัน : A\cap B=\{ x|x\in A และ x\in B \} อยู่ทั้งในเซต A และเซต B
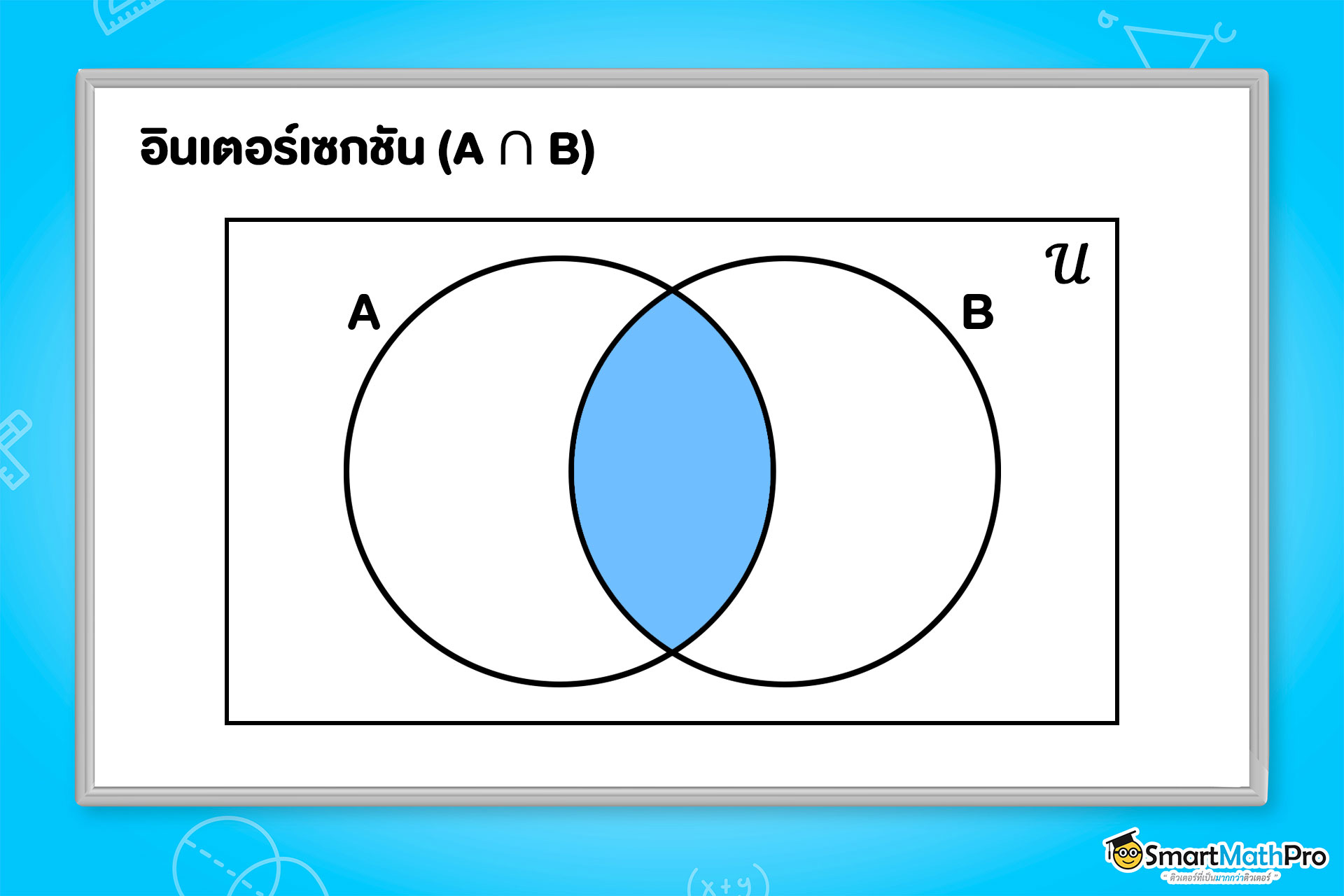
- ยูเนียน : A\cup B =\{ x|x\in A และ x\in B \} อยู่ในเซต A หรือ เซต B หรือทั้งคู่ก็ได้
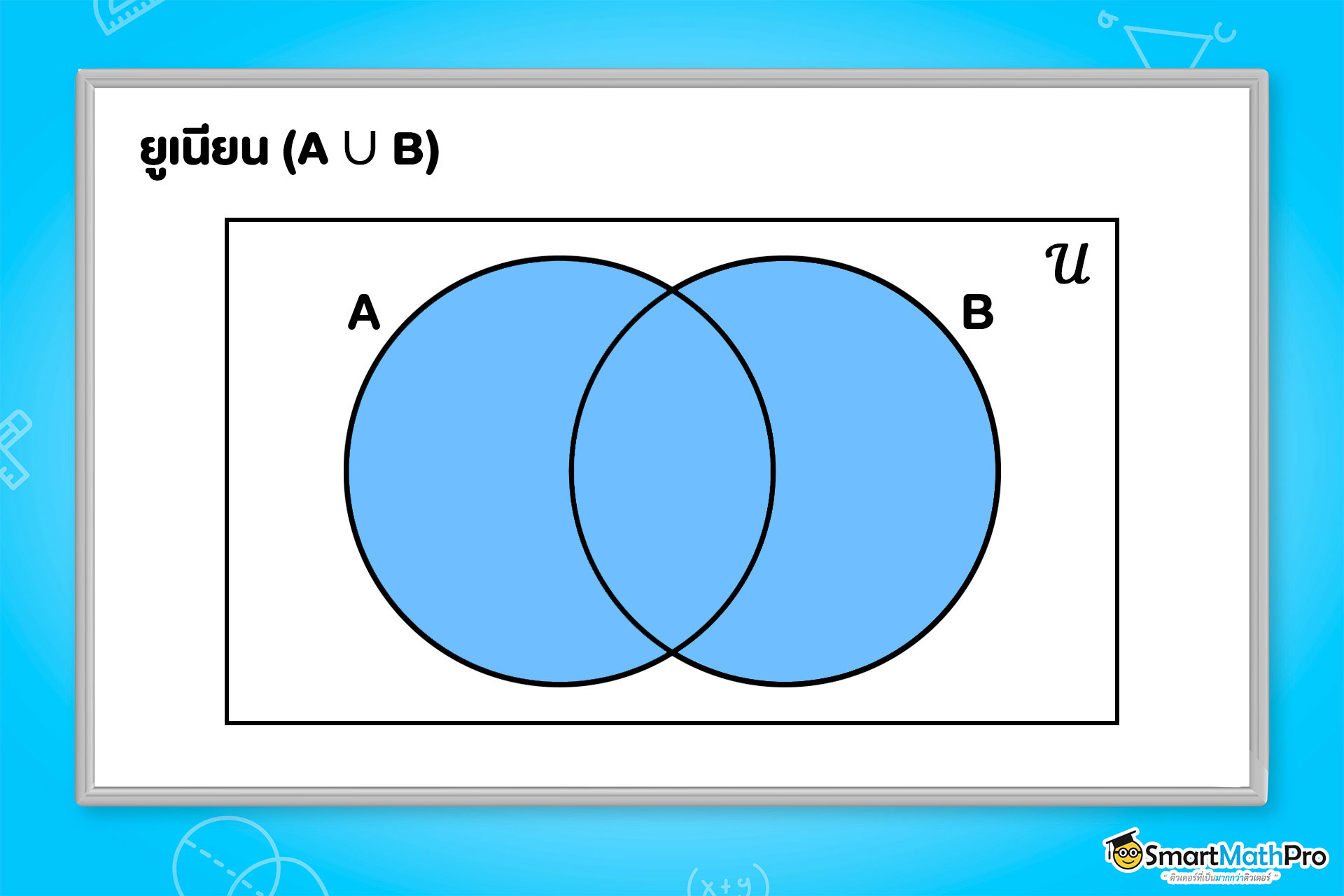
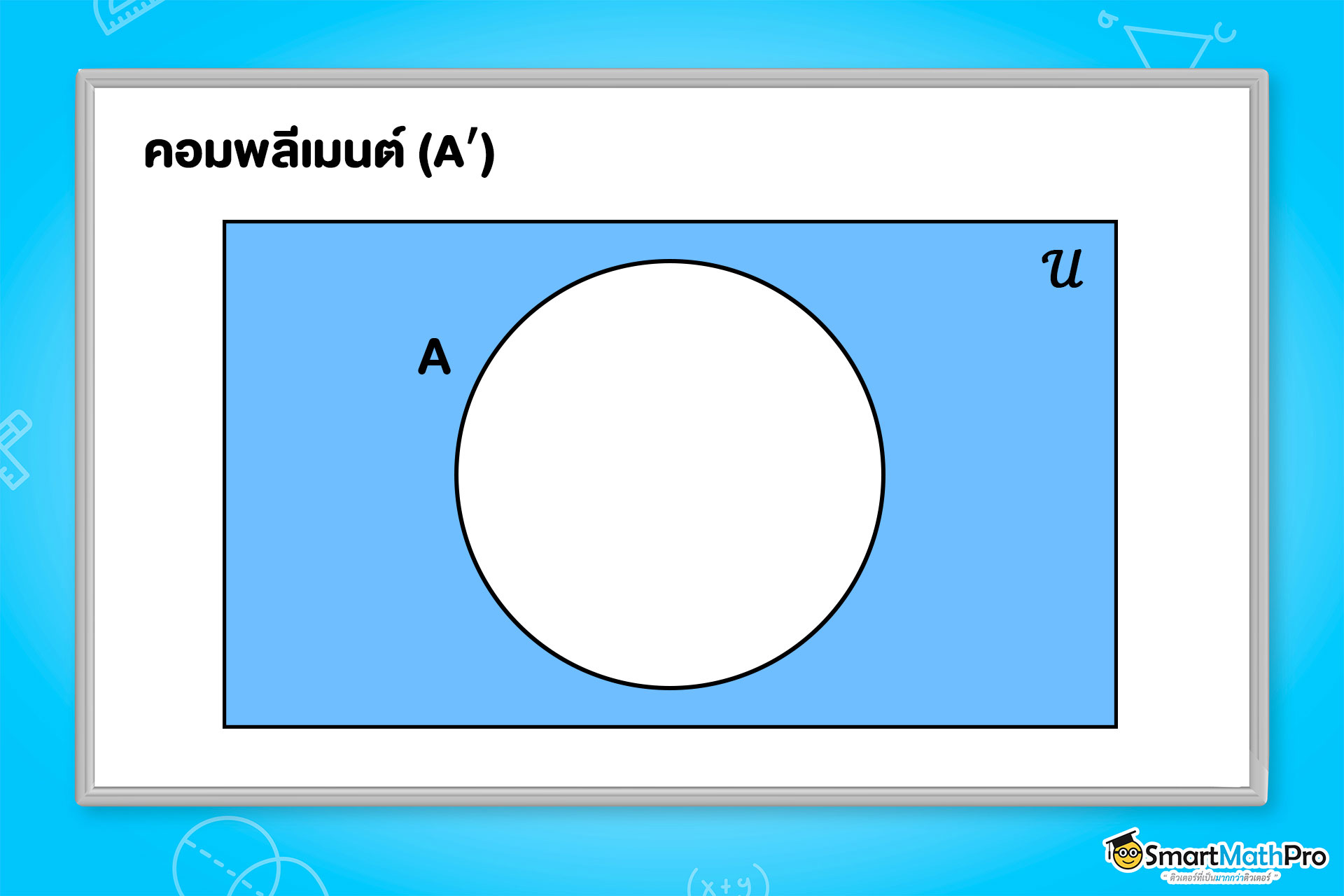
- คอมพลีเมนต์ : A′ =\{ x|x\in U และ x\notin A \} ไม่อยู่ในเซต A (แต่ยังอยู่ใน Uนะ)
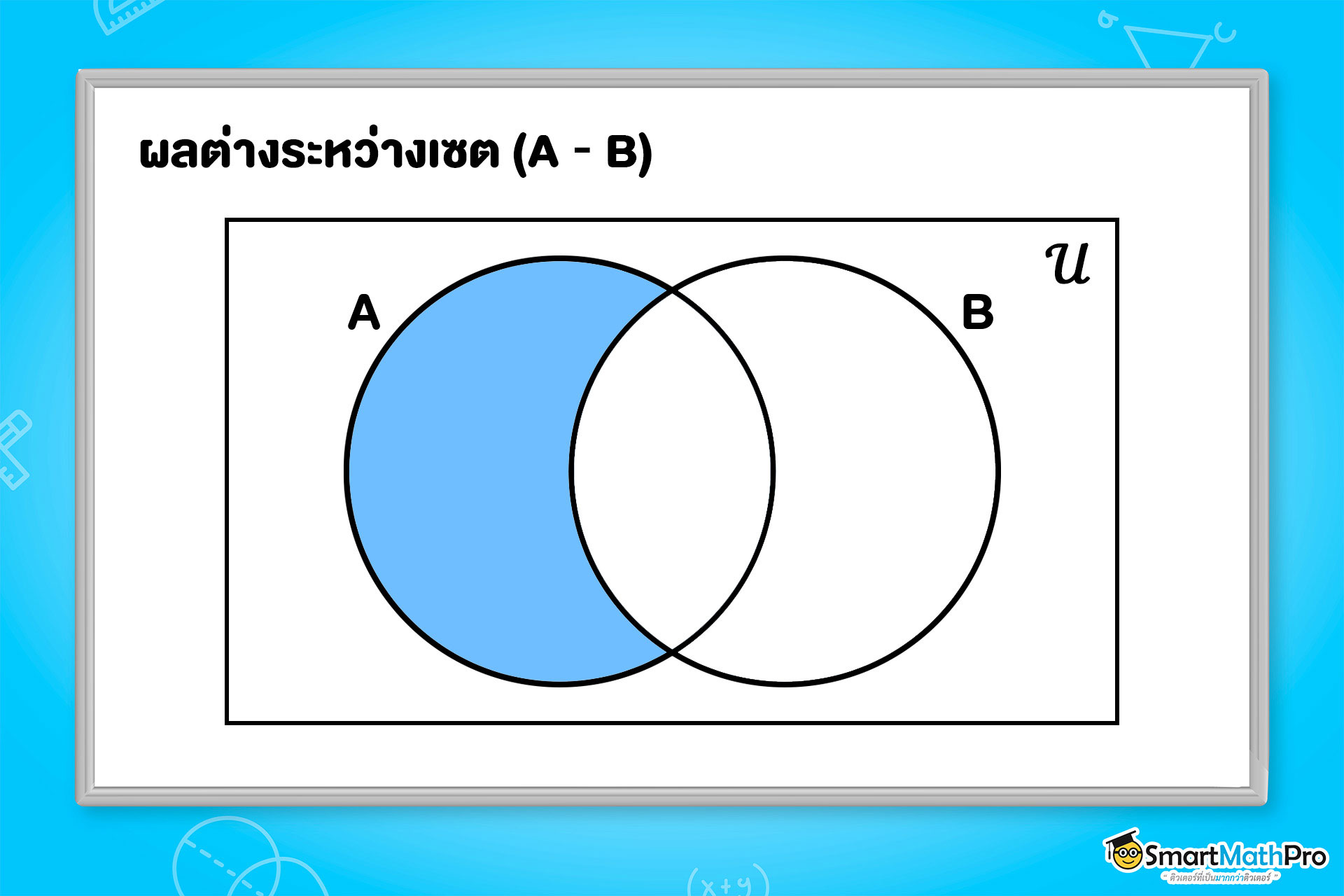
- ผลต่างระหว่างเซต : A-B= \{ x|x\in A และ x\notin B \} อยู่ในเซต A แต่ไม่อยู่ในเซต B
ตัวอย่างที่ 4
ให้ U = {1, 2, 3, 4, 5, 6}, A = {1, 5, 6}, B = {2, 4, 6} จะได้ว่า
- A\cap B = {6}
- A\cup B = {1, 2, 4, 5, 6}
- A – B = {1, 5}
- B – A = {2, 4}
- A′ = {2, 3, 4}
- B′ = {1, 3, 5}
สมบัติของการดำเนินการของเซต
การแก้ปัญหาโดยใช้เซต
มักใช้แผนภาพเวนน์มาใช้ร่วมกับสูตรจำนวนสมาชิก
สูตรจำนวนสมาชิกของเซต
- สำหรับ 2 เซต (แผนภาพเซต 2 วง)
n(A\cup B)=n(A)+n(B)-n(A\cap B)
- สำหรับ 3 เซต (แผนภาพเซต 3 วง
n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(A\cap C)-n(B\cap C)+n(A\cap B\cap C)
การแก้โจทย์ปัญหาโดยใช้เซต
ตัวอย่างที่ 5 จากการสำรวจนักเรียนจำนวน 40 คน เกี่ยวกับการเลี้ยงสัตว์ 3 ชนิด ได้แก่ แมว สุนัข และนก
ได้ผลสำรวจดังนี้
- 15 คน เลี้ยงแมว
- 17 คน เลี้ยงสุนัข
- 12 คน เลี้ยงนก
- 7 คน เลี้ยงแมวและสุนัข
- 4 คน เลี้ยงแมวและนก
- 5 คน เลี้ยงสุนัขและนก
- และ 3 คนที่เลี้ยงสัตว์ครบทั้ง 3 ชนิด
จากข้อมูลดังกล่าว จงตอบคำถามต่อไปนี้
- มีนักเรียนกี่คนที่เลี้ยงสัตว์เหล่านี้อย่างน้อย 1 ชนิด
- มีนักเรียนกี่คนที่ไม่ได้เลี้ยงสัตว์สามชนิดนี้เลย
วิธีทำ ในข้อนี้ เราจะนำเซตมาใช้แก้ปัญหา โดยเราจะกำหนดให้
A แทนเซตของนักเรียนที่เลี้ยงแมว n(A) = 15
B แทนเซตของนักเรียนที่เลี้ยงสุนัข n(B) = 17
C แทนเซตของนักเรียนที่เลี้ยงนก n(C) = 12
จากการกำหนดเซตข้างต้น ทำให้กลุ่มอื่น ๆ ในโจทย์ แทนด้วยเซตที่เกิดจากการดำเนินการระหว่างเซต ดังนี้
A\cap B แทนเซตของนักเรียนที่เลี้ยงแมวและสุนัข n(A\cap B)=7
A\cap C แทนเซตของนักเรียนที่เลี้ยงแมวและนก n(A\cap C)=4
B\cap C แทนเซตของนักเรียนที่เลี้ยงสุนัขและนก n(B\cap C)=5
และ A\cap B\cap C แทนเซตของนักเรียนที่เลี้ยงสัตว์ทั้ง 3 ชนิด n(A\cap B\cap C)=3
1.) กลุ่มของคนที่เลี้ยงสัตว์เหล่านี้อย่างน้อย 1 ชนิด (เลี้ยงแมว หรือสุนัข หรือนก โดยจะเลี้ยงหลายชนิดก็ได้)
แทนด้วยเซต A\cup B\cup C
จากสูตร 3 เซต n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(A\cap C)-n(B\cap C)+n(A\cap B\cap C)
จะได้ว่า n(A\cup B\cup C)=15+17+12-7-4-5+3=31
นั่นคือ มีนักเรียนที่เลี้ยงสัตว์เหล่านี้อย่างน้อย 1 ชนิด จำนวน 31 คน
ตอบ 31 คน
2.) กลุ่มของคนที่ไม่ได้เลี้ยงสัตว์สามชนิดนี้เลย แทนด้วยเซต (A\cup B\cup C)′
แต่เพื่อความง่าย สามารถมองได้ว่า
กลุ่มของคนที่ไม่ได้เลี้ยงสัตว์สามชนิดนี้เลย ตรงข้ามกับ กลุ่มของคนที่เลี้ยงสัตว์สามชนิดนี้อย่างน้อย 1 ชนิด
เนื่องจาก มีนักเรียนทั้งหมด 40 คน เป็นนักเรียนที่เลี้ยงสัตว์สามชนิดนี้อย่างน้อย 1 ชนิด เป็นจำนวน 31 คน
ดังนั้น จะมีนักเรียนที่ไม่ได้เลี้ยงสัตว์สามชนิดนี้เลย จำนวน 40 – 31 = 9 คน
ตอบ 9 คน
หากสร้างแผนภาพเวนน์เพื่อแสดงจำนวนของนักเรียนแต่ละกลุ่มย่อย จะได้ผลลัพธ์เป็นดังนี้
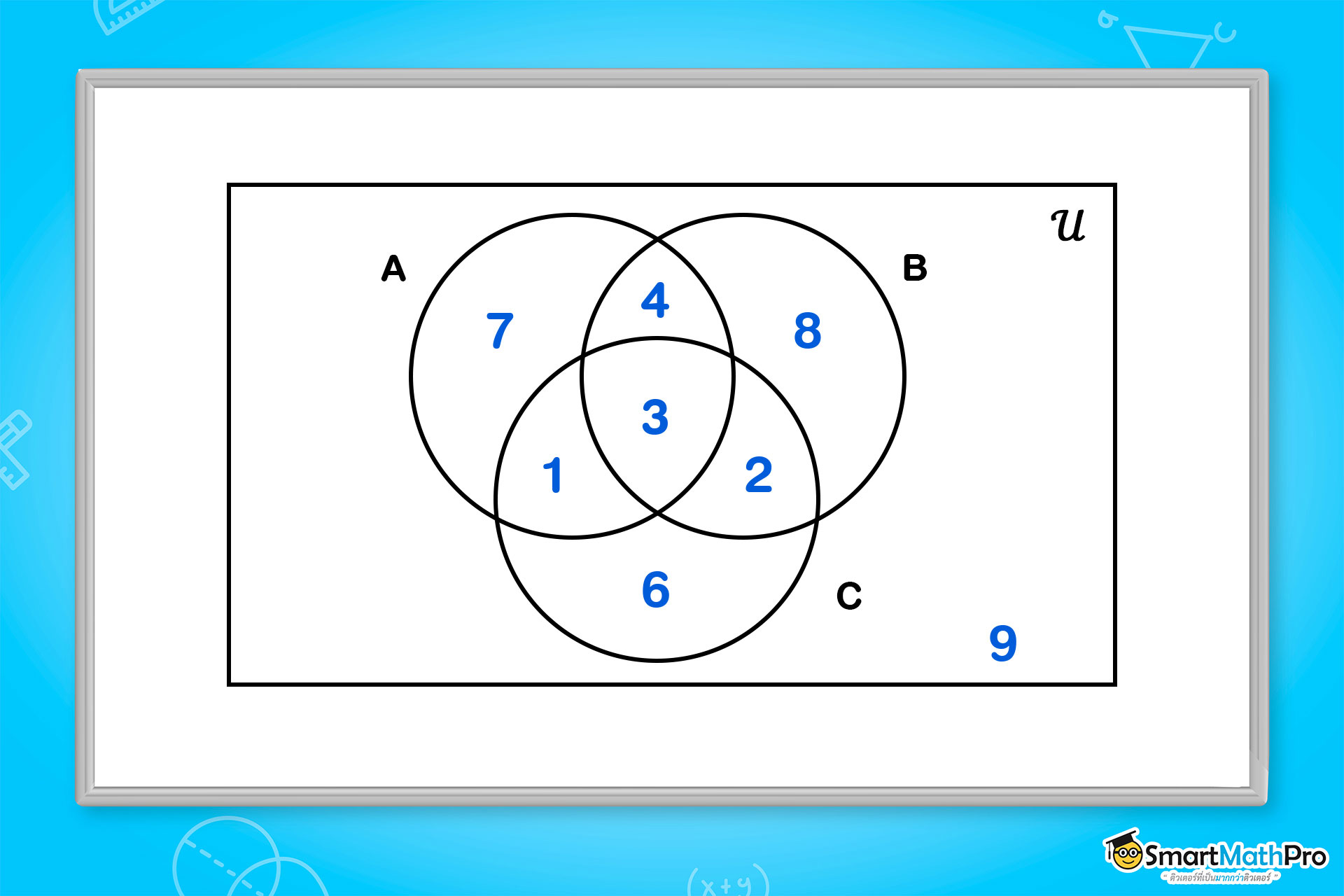
เป็นยังไงบ้างกับจากตัวอย่างโจทย์ที่พี่ยกมาให้น้อง ๆ ทั้งเนื้อหาและตัวอย่างโจทย์ คิดว่าน่าจะช่วยให้ทุกคนเข้าใจได้ในระดับหนึ่งเลยถูกมั้ยย แต่ถ้าใครอยากเก่งขึ้น พี่ก็แนะนำให้น้อง ๆ ลองดาวน์โหลดแบบฝึกหัด เซต ม.4 จากคลังข้อสอบมาฝึกทำเพิ่มจะดีกว่าน้าา เพราะการฝึกทำโจทย์จะช่วยทบทวนความเข้าใจของตัวเองด้วยนั่นเองง
ดูคลิปติวเรื่อง "เซต"
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
อ่านมาจนถึงตรงนี้ บางคนอาจจะเริ่มรู้สึกแล้วใช่ไหมว่า เนื้อหาคณิต ม.4 เรื่องเซตก็ไม่ได้ยากอย่างที่คิดเลยย ซึ่งน้อง ๆ จะเก่งเรื่องนี้ขึ้นได้อีกน้า ถ้าทบทวนเนื้อหาและฝึกทำโจทย์บ่อย ๆ
แต่ถ้าใครยังกังวลกลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้พี่ขอแนะนำคอร์สติวคณิตศาสตร์
ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลยยย
สุดท้ายพี่ก็อยากบอกกับทุกคนว่า ในช่วงแรก ๆ ถ้าใครเจอเนื้อหาที่ไม่เข้าใจ ก็ไม่อยากให้กังวลมากเกินไปน้าา แนะนำว่าเน้นทำความเข้าใจพื้นฐานของบทนั้นให้แม่นก่อน เพราะถ้าทุกคนมีพื้นฐานที่แข็งแรง ก็จะช่วยก็จะช่วยต่อยอดในบทอื่น ๆ ได้เองอย่างที่พี่บอกไว้ตอนแรกเลย หรือจะดาวน์โหลดเอกสารรวม 10 จุดระวังเรื่อง เซต เอาไว้ทบทวนก็ได้น้า จะได้เข้าใจยิ่งขึ้น แล้วก็ค่อยฝึก ๆ ไป พี่เชื่อว่าทุกคนทำได้แน่นอนน พี่เป็นกำลังใจให้ทุกคนเลยย
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
คณิตศาสตร์ ม.4 เทอม 1 และเทอม 2 เรียนอะไรบ้าง ? สรุปครบทั้งคณิตพื้นฐานและเพิ่มเติม
ตรรกศาสตร์ ม.4 สรุปครบทุกเนื้อหาพร้อมโจทย์ตรรกศาสตร์และวิธีทำ – SmartMathPro
จำนวนจริง ม.4 สรุปครบม้วนเดียวจบ พร้อมแจกโจทย์จำนวนจริงและวิธีทำ
ความสัมพันธ์และฟังก์ชัน ม.4 สรุปเนื้อหาพร้อมแจกโจทย์ให้ฝึกทำ !
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
