ถ้าพูดถึงสมการ น้อง ๆ อาจจะคุ้นเคยกับการแก้สมการที่แทนค่าตัวแปรใดตัวแปรหนึ่งเพื่อให้ได้คำตอบ แต่รู้ไหมว่าในเนื้อหาคณิต ม.3 นี้ ยังมีสมการอีกรูปแบบหนึ่งที่น้อง ๆ จะได้เรียนด้วย นั่นก็คือ ระบบสมการเชิงเส้นสองตัวแปร ซึ่งเป็นการหาคำตอบของสมการสองชุด ที่มีตัวแปรถึงสองตัวนั่นเอง
แต่ไม่ต้องกังวลไปน้าาา เดี๋ยวพี่จะพาทุกคนไปทำความเข้าใจเนื้อหาบทนี้แบบเข้าใจง่ายที่สุด พาทำโจทย์พร้อมเฉลยละเอียด นอกจากนี้ยังมีคลิปติวฟรีท้ายบทความ และแบบฝึกหัดให้ดาวน์โหลดไปลองฝึกทำด้วย ถ้าน้อง ๆ พร้อมกันแล้วตามพี่ไปอ่านกันเลยยยย
ระบบสมการเชิงเส้น คือ ชุดสมการที่มีเลขชี้กำลังเป็น 1 ตั้งแต่ 2 สมการขึ้นไป ที่ทุกสมการมีตัวแปรชุดเดียวกัน
โดยความรู้ในบทนี้จะใช้เป็นพื้นฐานสำหรับคณิตม.ปลายอีกหลายบทเลย เช่น บทเมทริกซ์ ที่นำการแก้ระบบสมการเชิงเส้นมาประยุกต์ใช้ ซึ่งมีจำนวนสมการตั้งแต่ 2 สมการ หรือมีตัวแปรตั้งแต่ 2 ตัวแปรขึ้นไป
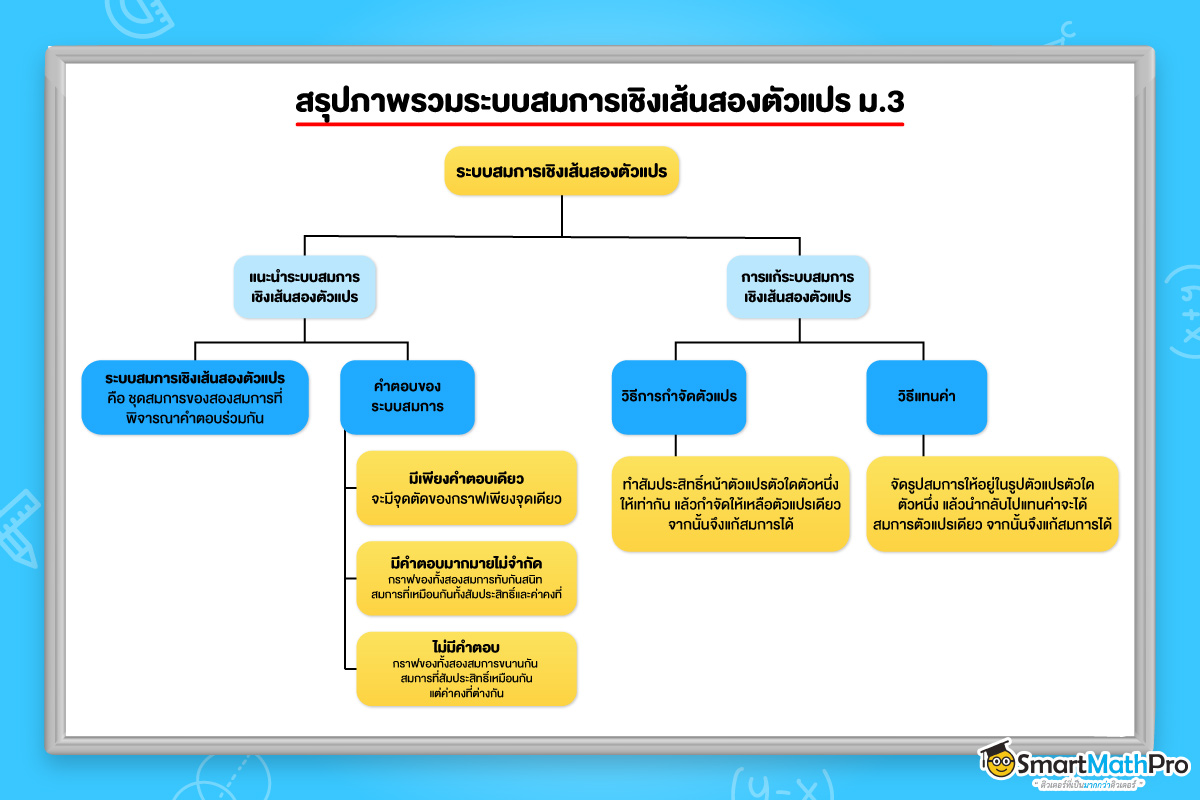
ความหมายของระบบสมการเชิงเส้นสองตัวแปร
ระบบสมการเชิงเส้นสองตัวแปร (system of linear equations with two variables)
คือ ชุดสมการเชิงเส้นสองสมการสองตัวแปรที่พิจารณาคำตอบร่วมกัน
คำตอบของระบบสมการเชิงเส้นสองตัวแปร
คำตอบของระบบสมการเชิงเส้นสองตัวแปร คือ คู่อันดับ (x, y) ที่ค่า x และค่า y ทำให้สมการเป็นจริงทั้งสองสมการ
น้อง ๆ จำกันได้ไหมว่าคู่อันดับ (x, y) จะสอดคล้องกับสมการ หรือเรียกว่าเป็นคำตอบของสมการก็ต่อเมื่อ มีการแทนค่า x และ y ลงไปในสมการนั้นแล้วทำให้สมการเป็นจริง
คราวนี้คู่อันดับ (x, y) จะเป็นคู่อันดับที่สอดคล้องกับระบบสมการเชิงเส้นสองตัวแปร Ax+By+C=0 ก็ต่อเมื่อแทนค่า x และค่า y ของแต่ละคู่อันดับนั้นในสมการแล้วทำให้ได้สมการที่เป็นจริง ซึ่งจะเรียกคู่อันดับที่สอดคล้องเหล่านั้นว่า คำตอบของระบบสมการเชิงเส้นสองตัวแปร และกราฟแสดงคำตอบของสมการ Ax+By+C=0 จะเป็นเส้นตรง เราเรียกเส้นตรงนี้ว่า เส้นตรง Ax+By+C=0
ดังนั้น คำตอบของระบบสมการที่กรอบข้างบนพูดถึง คือ จุดตัด (x, y) ของกราฟของเส้นตรงที่เกิดจากสมการเส้นตรง
ทั้งสองนั่นเอง
ตัวอย่างที่ 1 จงเขียนกราฟและหาคำตอบของระบบสมการเชิงเส้นสองตัวแปรต่อไปนี้
3x-y=3
2x+y=2
แนวคิด หาจุดตัดแกน X และ Y ของ 3x-y=3 และ 2x+y=2 เพื่อวาดกราฟ และพิจารณาจุดที่กราฟตัดกัน
ซึ่งจุดนั้นจะเป็นคำตอบของระบบสมการนี้
วิธีทำ จากสมการ 3x-y=3 เมื่อแทน x=0 จะได้ y=-3
ดังนั้น จุดตัดแกน Y คือ (0, -3)
และเมื่อแทน y=0 จะได้ x=1
ดังนั้น จุดตัดแกน X คือ (1, 0)
ในทำนองเดียวกัน จากสมการ 2x+y=2 เมื่อแทน x=0 จะได้ y=2
ดังนั้น จุดตัดแกน Y คือ (0, 2)
และเมื่อแทน y=0 จะได้ x=1
ดังนั้น จุดตัดแกน X คือ (1, 0)
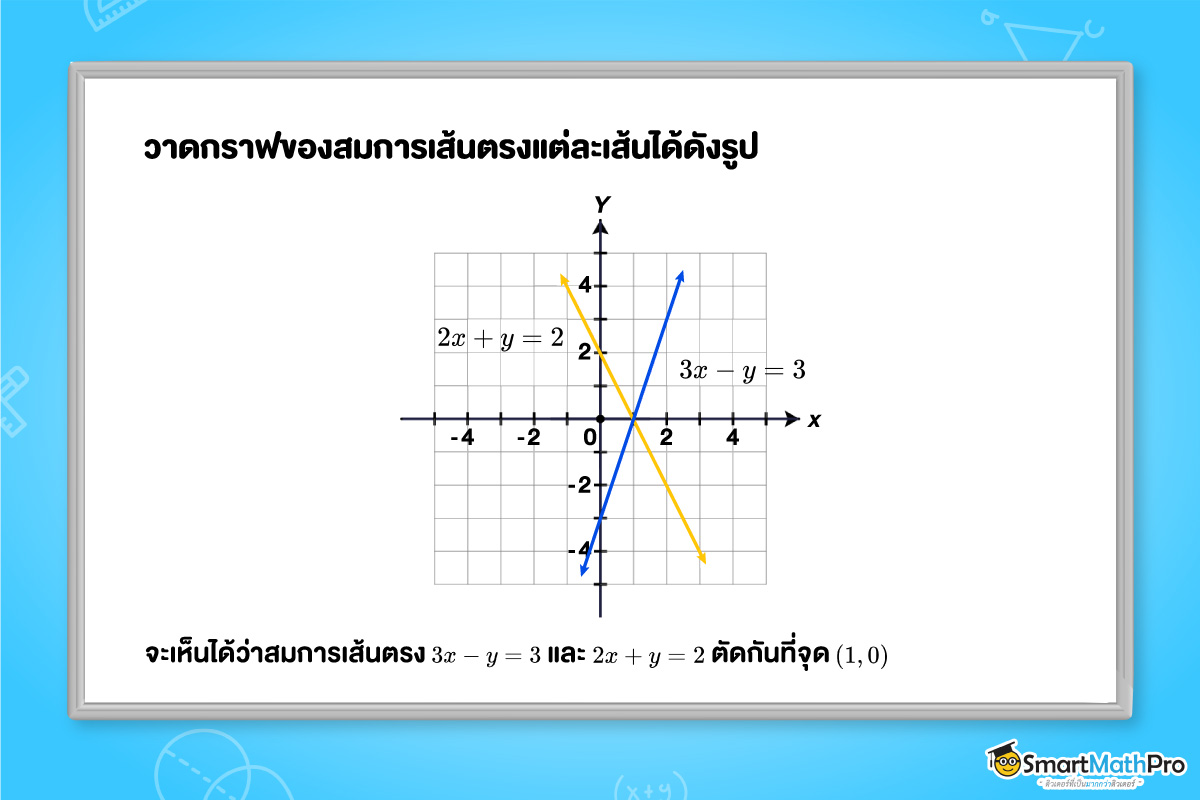
ตอบ ดังนั้นคำตอบของระบบสมการเชิงเส้นสองตัวแปร คือ (1, 0)
คำตอบของระบบสมการที่น้อง ๆ เห็นจากตัวอย่างก่อนหน้ามีคำตอบเดียว แต่จริง ๆ แล้วคำตอบของระบบสมการเชิงเส้นสองตัวแปร มี 3 รูปแบบ ดังนี้
- ระบบสมการที่มีคำตอบเพียงคำตอบเดียว กราฟของสมการจะตัดกันเพียงจุดเดียว
- ระบบสมการที่มีคำตอบมากมายไม่จำกัด กราฟของสมการจะทับกัน
โดยสมการทั้งสองมีสัมประสิทธิ์ที่เท่ากัน และค่าคงตัวเท่ากัน - ระบบสมการที่ไม่มีคำตอบ กราฟของสมการจะขนานกัน (ไม่ตัดกัน)
โดยสมการทั้งสองมีสัมประสิทธิ์ที่เท่ากัน แต่ค่าคงตัวไม่เท่ากัน
ให้น้อง ๆ สังเกตรูปแบบคำตอบของระบบสมการเชิงเส้นสองตัวแปรแต่ละรูปแบบผ่านกราฟต่อไปนี้
สมการที่ 1 และ 5 : กราฟของสมการทับกัน
สมการที่ 5 เมื่อจัดรูปสมการจะได้ y-x=2 เช่นเดียวกับสมการที่ 1
ดังนั้น ระบบสมการนี้มีคำตอบมากมายไม่จำกัดสมการที่ 2 และ 3 : กราฟของสมการขนานกัน
สมการที่ 3 เมื่อจัดรูปสมการจะได้ y+3x=-3 ซึ่งมีสัมประสิทธิ์ที่เท่ากันกับสมการที่ 2
แต่ค่าคงตัวไม่เท่ากัน
ดังนั้น ระบบสมการนี้ไม่มีคำตอบสมการที่ 1 หรือ 5 กับสมการที่ 2 : กราฟของสมการตัดกัน 1 จุด
ดังนั้น ระบบสมการนี้มี 1 คำตอบ
โดยจุดตัด คือ (1, 3)
จะได้ว่าคำตอบของระบบสมการ คือ (1, 3)สมการที่ 1 หรือ 5 กับสมการที่ 3 : กราฟของสมการตัดกัน 1 จุด
ดังนั้น ระบบสมการนี้มี 1 คำตอบ
โดยจุดตัด คือ (-1.25, 0.75)
จะได้ว่าคำตอบของระบบสมการ คือ (-1.25, 0.75)สมการที่ 1 หรือ 5 กับสมการที่ 4 : กราฟของสมการตัดกัน 1 จุด
ดังนั้น ระบบสมการนี้มี 1 คำตอบ
โดยจุดตัด คือ (-5, -3)
จะได้ว่าคำตอบของระบบสมการ คือ (-5, -3)
การแก้ระบบสมการเชิงเส้นสองตัวแปร
น้อง ๆ บางคนอาจจะเคยรู้มาว่า “การแก้สมการ” เป็นการหาคำตอบทั้งหมดของสมการ ซึ่งวิธีที่ใช้ในหัวข้อที่แล้ว คือ
การหาคำตอบจากกราฟของสมการเชิงเส้นสองตัวแปร แต่อาจมีปัญหาเรื่องการอ่านพิกัดที่เป็นคำตอบของสมการ เพราะเมื่อวาดกราฟเองด้วยมือ ไม่ได้ใช้คอมพิวเตอร์ช่วย อาจจะวาดแล้วกราฟเบี้ยว หรือสเกลบนแกน X หรือแกน Y ไม่ได้มีระยะห่างที่ถูกต้องเป๊ะ ๆ อาจทำให้เกิดความคลาดเคลื่อนจากค่าที่แท้จริงได้
เราจึงไม่นิยมใช้วิธีวาดกราฟเพื่อหาคำตอบของระบบสมการ รวมถึงบางครั้งคำตอบของระบบสมการอาจเป็นตัวเลขที่มีจำนวนเยอะมาก ๆ หรือติดเป็นเศษส่วนก็ได้ ซึ่งการมองจากจุดตัดกราฟอาจไม่ได้คำตอบที่ถูกต้องแม่นยำ
เพื่อความถูกต้องของการหาคำตอบของระบบสมการ เราจะใช้สมบัติของการเท่ากัน เช่น สมบัติสมมาตร สมบัติการถ่ายทอด สมบัติของการเท่ากันเกี่ยวกับการบวก และสมบัติของการเท่ากันเกี่ยวกับการคูณ มาช่วยในการหาคำตอบ ซึ่งวิธีการทำจะมีหลัก ๆ ทั้งหมด 2 วิธี คือ
- การแก้ระบบสมการด้วยวิธีกำจัดตัวแปร
- การแก้ระบบสมการด้วยวิธีแทนค่าตัวแปร
การแก้ระบบสมการด้วยวิธีกำจัดตัวแปร
วิธีนี้จะต้องแก้ระบบสมการโดยพิจารณาจากสัมประสิทธิ์ของแต่ละตัวแปรว่าค่าของสัมประสิทธิ์นั้นเท่ากัน ตรงข้ามกัน หรือต่างกัน ซึ่งจะมีวิธีการกำจัดตัวแปรดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 2 กำหนดให้ x และ y เป็นจำนวนจริงใด ๆ จงหาคำตอบของระบบสมการนี้
2x+y=-1
x-y=4
แนวคิด สัมประสิทธิ์ของ y เป็น 1 และ -1 ซึ่งตรงข้ามกัน ดังนั้นสามารถกำจัดตัวแปร y ได้โดยได้โดยการนำสมการมาบวกกัน
วิธีทำ
2x+y=-1 ______ (1)
x-y=4 ______ (2)
(1)+(2) ;
(2x+y)+(x-y)=(-1)+4
3x=3
x=1
แทน x ด้วย 1 ในสมการ (2)
จะได้
1-y=4
-y=3
y=-3
ดังนั้น ระบบสมการนี้มีคำตอบ คือ (1, -3)
การแก้ระบบสมการด้วยวิธีแทนค่า
วิธีนี้จะจัดรูปสมการใหม่ โดยให้ตัวแปรอยู่ในรูปของตัวแปรอีกตัวหนึ่ง แล้วแทนตัวแปรที่ได้ลงในอีกสมการ เพื่อให้ได้สมการใหม่ที่มีตัวแปรเพียงตัวเดียว จากนั้นแก้สมการ เพื่อให้ได้ค่าของตัวแปรต่อไป ซึ่งการแก้ระบบสมการด้วยวิธีแทนค่ามีขั้นตอนดังนี้
ขั้นตอนที่ 1 : กำหนดชื่อของสมการ
ขั้นตอนที่ 2 : จัดรูป
ขั้นตอนที่ 3 : แทนค่าตัวแปร
ขั้นตอนที่ 4 : หาค่าของตัวแปรที่เหลือ
ตัวอย่างที่ 3 กำหนดให้ x และ y เป็นจำนวนจริงใด ๆ จงหาคำตอบของระบบสมการนี้
-2x+y=5
6x-2y=-8
วิธีทำ
ขั้นตอนที่ 1 : กำหนดชื่อของสมการ
-2x+y=5 ______ (1)
6x-2y=-8 ______ (2)
ขั้นตอนที่ 2 : จัดรูป (เขียนตัวแปร y ให้อยู่ในรูปของตัวแปร x)
จาก (1) จะได้
y=2x+5 ______ (3)
ขั้นตอนที่ 3 : แทนค่าตัวแปร (เป็นการทำเพื่อให้ได้สมการที่มี x เป็นตัวแปรเพียงตัวเดียว)
จาก (3)
แทน y ด้วย 2x+5 ในสมการ (2) จะได้
6x-2(2x+5)=-8
6x-4x-10=-8
2x=2
x=1
ขั้นตอนที่ 4 : หาค่าของตัวแปรที่เหลือ
แทน x ด้วย 1 ในสมการ (1) จะได้
-2(1)+y=5
-2+y=5
y=7
ดังนั้น ระบบสมการนี้มีคำตอบ คือ (1, 7)
ดูคลิปติว ระบบสมการเชิงเส้นสองตัวแปร ม.3
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
เป็นยังไงกันบ้างกับเนื้อหา ระบบสมการเชิงเส้นสองตัวแปร ม.3 ที่พี่สรุปมาให้อ่านกันในวันนี้ บอกเลยว่าถ้าน้อง ๆ เข้าใจเรื่องนี้ ก็จะสามารถนำไปใช้ต่อยอดกับคณิต ม.ปลายได้อีกด้วย ดังนั้นถ้าอ่านบทความนี้จบแล้วพี่ก็แนะนำให้ลองทำ
แบบฝึกหัดระบบสมการเชิงเส้นสองตัวแปร ม.3 เพิ่มเติมด้วยน้า จะได้ช่วยวัดความเข้าใจของเราด้วยว่ายังมีจุดไหนที่เรา
ไม่เข้าใจอยู่หรือเปล่า
ซึ่งสำหรับน้อง ๆ ที่กำลังเผชิญปัญหาดังกล่าวอยู่ และต้องการคนช่วยไกด์เนื้อหาระบบสมการเชิงเส้นสองตัวแปร รวมถึงเนื้อหาคณิต ม.3 บทอื่น ๆ ให้เข้าใจมากขึ้น พี่ขอแนะนำคอร์สติวคณิต ม.3 จาก SmartMathPro เลยย คอร์สนี้มีทั้งเนื้อหาของทั้งเทอม 1 และเทอม 2 ครบทุกบท ซึ่งพี่จะปูพื้นฐานให้แบบละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. พร้อมพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ แถมยังมี Quiz ทบทวนความเข้าใจแต่ละบทให้ด้วยน้า ดังนั้นใครที่พื้นฐานไม่แน่นก็เรียนได้ ไม่ต้องกังวลเลยว่าจะเรียนไม่ทัน !!
แต่ถ้าโรงเรียนของน้อง ๆ สอนไม่ตรงตามคอร์สที่มี ก็สามารถเลือกเรียนแบบแยกบทได้เลยย เริ่มต้นเพียง 360 บาทเท่านั้น ใครสนใจดูรายละเอียดเพิ่มเติม คลิก ได้เลย
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สรุป พาราโบลา (ฟังก์ชันกำลังสอง) ม.3 พร้อมแจกสูตรและโจทย์ฟรี
สถิติ ม.3 (แผนภาพกล่อง) สรุปเนื้อหา พร้อมแจกโจทย์และเฉลยฟรี!
สรุป วงกลม ม.3 ทฤษฎีบทวงกลม พร้อมแจกแบบฝึกหัดฟรี !
ตรีโกณมิติ ม.3 สรุปเนื้อหาพร้อมโจทย์แบบจัดเต็ม จบในที่เดียว !
สรุป ความน่าจะเป็น ม.3 พร้อมแจกโจทย์และเฉลยฟรี!!
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
