มีใครรู้สึกมั้ยยยยย ว่าพอขึ้นม.5 เนื้อหาวิชาคณิตศาสตร์ก็ยิ่งซับซ้อนขึ้น จนทำให้น้อง ๆ หลายคนกลัวว่าจะเรียนไม่เข้าใจ ซึ่งถ้าใครกำลังกังวลเรื่องนี้อยู่ก็ไม่ต้องห่วงน้าา เพราะวันนี้พี่เอาหนึ่งในบทเรียนของคณิต ม.5 เทอม 1 อย่างเรื่องเมทริกซ์ มาสรุปเนื้อหาให้น้อง ๆ เข้าใจมากขึ้นแล้ว !!
โดยเนื้อหาที่พี่เตรียมมาก็จะมีตั้งแต่ความรู้เบื้องต้นเกี่ยวกับเมทริกซ์, การบวก การลบ และการคูณเมทริกซ์ และเรื่องอื่น ๆ อีกมากมาย นอกจากนี้ยังมีตัวอย่างโจทย์พร้อมวิธีทำ แถมท้ายบทความพี่มีแจกแบบฝึกหัดเมทริกซ์ ม.5 ให้ไปฝึกทำด้วย ใครอยากรู้แล้วก็รีบเลื่อนลงไปดูกันได้เลยยย
จากในชีวิตประจำวันน้อง ๆ น่าจะเคยเห็นการนำเสนอข้อมูลผ่านตารางมาบ้างแล้ว ในทางคณิตศาสตร์ การใช้ตารางก็คือวิธีหนึ่งในการนำเสนอข้อมูลและจัดการข้อมูล โดยเราจะนำข้อมูลที่อยู่ในรูปตารางมาเขียนให้อยู่ภายใต้วงเล็บ ( ) หรือ [ ] ก็ได้ แต่ว่าในบทเรียนที่น้อง ๆ จะได้เรียนในบทนี้เราจะใช้วงเล็บแบบเหลี่ยม [ ] และเราจะเรียกว่า “เมทริกซ์”
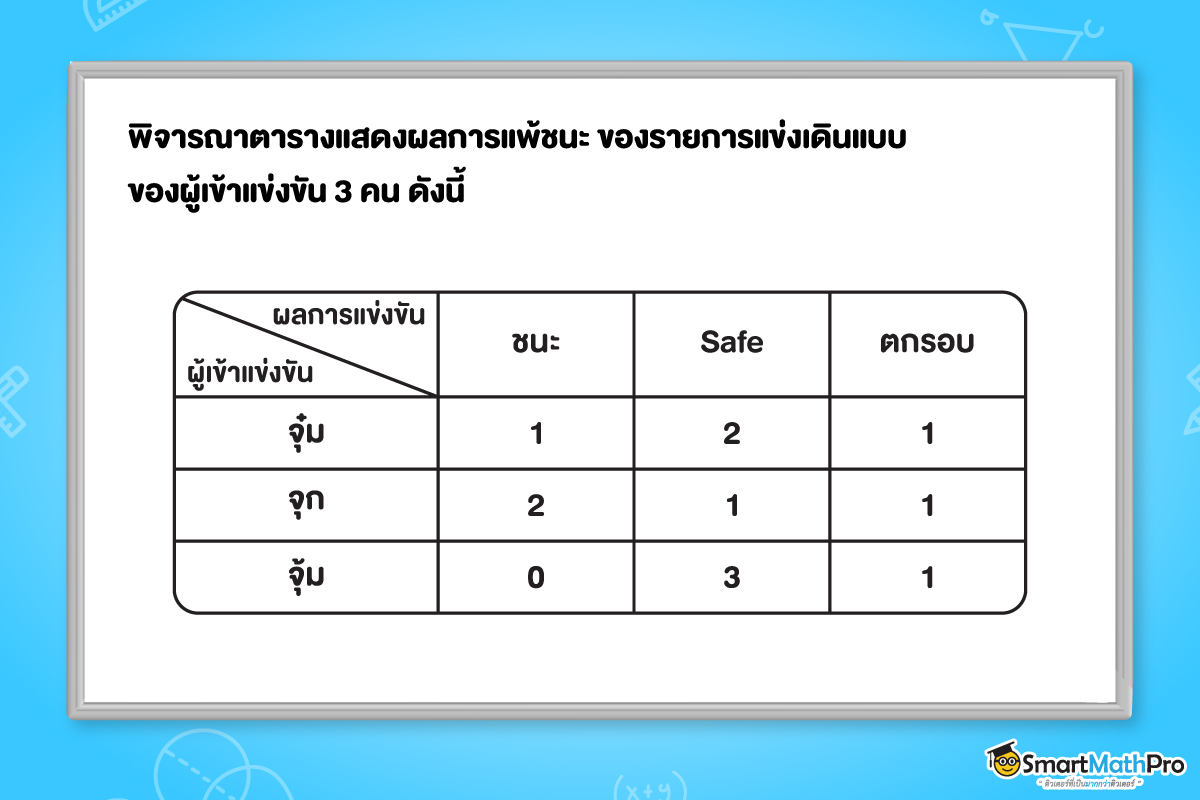
จากตารางข้างต้นถ้าเราลองนำมาเขียนให้เป็นเมทริกซ์ ก็เพียงแค่นำข้อมูลมาใส่ไว้ในกรอบ [ ] ก็จะได้
\begin{bmatrix}1 &2 &1 \\ 2 &1 &1 \\ 0 &3 &1 \end{bmatrix}
เราก็พอจะเห็นกันคร่าว ๆ แล้วใช่ไหม ว่าเมทริกซ์มีรูปร่างหน้าตาเป็นอย่างไรบ้าง เราไปทำความรู้จักเมทริกซ์เพิ่มเติมในหัวข้อถัดไปกันเถอะ
ความรู้เบื้องต้นเกี่ยวกับเมทริกซ์
แถวและหลักของเมทริกซ์
บทนิยามต่อไปนี้จะกล่าวถึงส่วนประกอบต่าง ๆ ของเมทริกซ์นะ โดยคำศัพท์ทั้งหลายมักจะใช้ไปตลอดทั้งบทนี้เลย ไม่ว่าจะเป็น “แถว” “หลัก” หรือคำศัพท์อื่น ๆ อย่าง “สมาชิก” “ขนาด” “มิติ” เพื่อให้เราเข้าใจได้ตรงกันและเรียกชื่อส่วนต่าง ๆ ได้ถูกต้อง ลองไปดูบทนิยามด้วยกันเลยย
บทนิยาม
ให้ m และ n เป็นจำนวนเต็มบวก ชุดของจำนวนจริง mn จำนวน ซึ่งเรียงกันในรูป
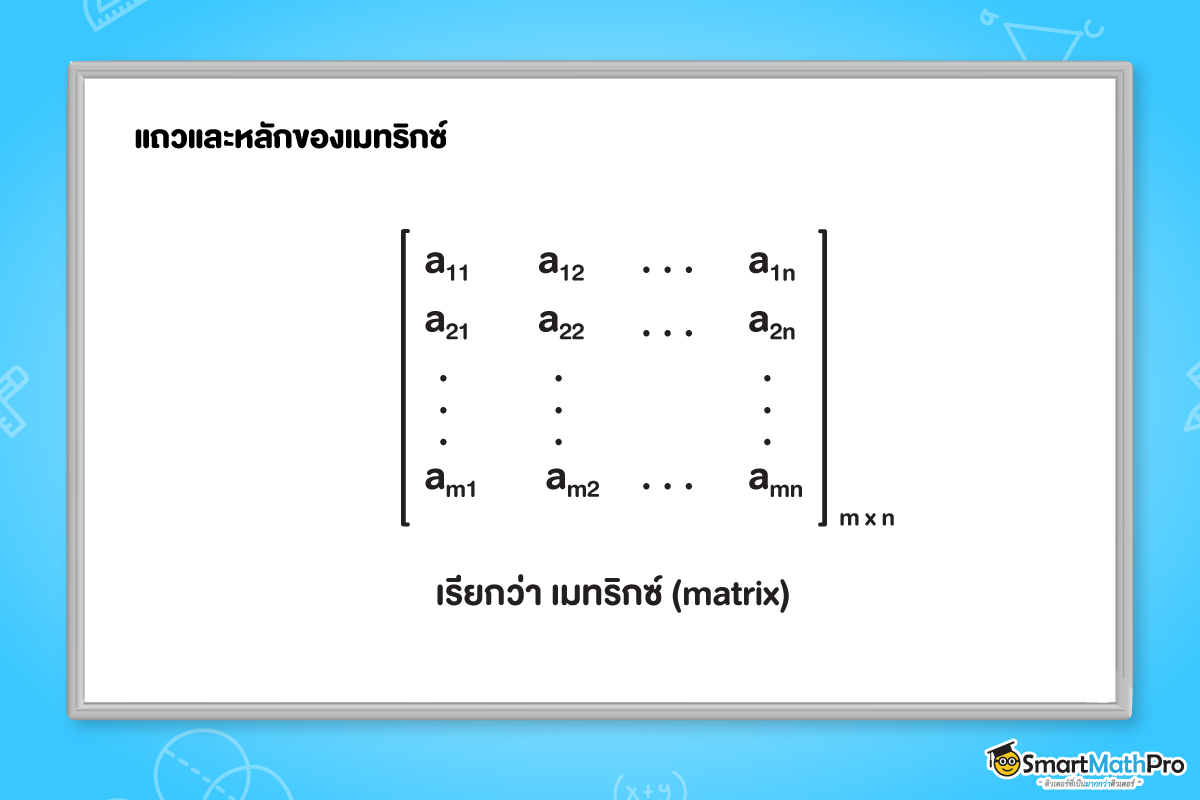
จากรูปชุดของสมาชิกที่เขียนในแนวนอน เรียกว่า แถว (row) ของเมทริกซ์ ซึ่งมีทั้งหมด m แถว
ชุดของสมาชิกที่เขียนในแนวตั้ง เรียกว่า หลัก (column) ของเมทริกซ์ ซึ่งมีทั้งหมด n หลัก
เรียก a_{ij} ว่าเป็น สมาชิก (entry) ในแถวที่ i และหลักที่ j ของเมทริกซ์
ถ้าเมทริกซ์มี m แถว n หลัก จะเรียก m\times n ว่า ขนาด (size) หรือ มิติ (dimension) ของเมทริกซ์
ตัวอย่างที่ 1 กำหนดให้ A=\begin{bmatrix} 1 &2 &0 \\ -2 &4 &-1 \end{bmatrix} จงหา
1. a_{12}
วิธีทำ จาก a_{12} คือสมาชิกในแถวที่ 1 หลักที่ 2
จะได้ว่า a_{12}=2
2. a_{13}
วิธีทำ จาก a_{13} คือสมาชิกในแถวที่ 1 หลักที่ 3
จะได้ว่า a_{13}=0
3. a_{22}
วิธีทำ จาก a_{22} คือสมาชิกในแถวที่ 2 หลักที่ 2
จะได้ว่า a_{22}=4
การเท่ากันของเมทริกซ์
เมทริกซ์สองเมทริกซ์จะเท่ากันได้ต้องมีลักษณะตามนิยามต่อไปนี้เลย
บทนิยาม
ให้ A= [a_{ij}]_{m\times n} และ B=[b_{ij}]_{p\times q}
A เท่ากับ B ก็ต่อเมื่อ m=p, n=q และ a_{ij}=b_{ij} สำหรับทุก i\in \left \{1, 2, 3, …, m \right \} และ j\in \left \{1, 2, 3, …, n \right \}
เขียนแทน A เท่ากับ B ด้วย A=B
จากบทนิยามข้างต้นถ้าพี่จะสรุปให้น้องเข้าใจได้ง่าย ๆ ก็คือ
เมทริกซ์จะเท่ากันได้ต้องมีขนาดเท่ากัน และในสมาชิกตำแหน่งเดียวกัน ต้องมีค่าเท่ากัน
ตัวอย่างที่ 2 กำหนดให้ \begin{bmatrix}1 &x \\ 0 &3 \end{bmatrix}=\begin{bmatrix}1 &2 \\ y-1 &3 \end{bmatrix} จงหาค่าของ x และ y
แนวคิด จากการเท่ากันของเมทริกซ์ สมาชิกในตำแหน่งเดียวกันต้องมีค่าเท่ากัน ให้น้อง ๆ นำสมาชิกในตำแหน่งเดียวกันมาเชื่อมด้วยเครื่องหมายเท่ากับ และแก้สมการหาค่าของ x และ y
วิธีทำ จากบทนิยาม
จะได้ว่า x=2
และ y-1=0 นั่นคือ y=1
ดังนั้น x=2 และ y=1
เมทริกซ์สลับเปลี่ยน (transpose of a matrix)
น้อง ๆ บางคนอาจจะเคยได้ยินหรือคุ้นชินกับเมทริกซ์สลับเปลี่ยนในอีกชื่อหนึ่งคือ transpose of a matrix ซึ่ง transpose (ทรานสโพส) หมายถึงการเปลี่ยนตำแหน่ง ในหัวข้อนี้เราจะมาสลับตำแหน่งของสมาชิกในเมทริกซ์กัน โดยมาดูนิยามของเมทริกซ์สลับเปลี่ยนกันก่อนว่าตำแหน่งของสมาชิกในเมทริกซ์จะเปลี่ยนไปอย่างไรบ้าง
บทนิยาม
ให้ A=[a_{ij}]_{m\times n} และ B=[b_{ij}]_{n\times m} โดยที่ b_{ij}=a_{ji}
สำหรับทุก i\in \left \{1, 2, 3, …, n \right \} และ j\in \left \{1, 2, 3, …, m \right \}
แล้วจะเรียก B ว่า เมทริกซ์สลับเปลี่ยน (transpose of a matrix) ของ A เขียนแทนด้วย A^t
จากบทนิยามในกรอบข้างต้นถ้าพี่จะสรุปให้เข้าใจกันแบบง่าย ๆ ก็จะได้ว่า
เมทริกซ์สลับเปลี่ยน คือ การเรียงสมาชิกใหม่ โดยนำแถวไปเป็นหลัก นำหลักไปเป็นแถว
ตัวอย่างที่ 3
ให้ A=\begin{bmatrix}1 &2 \\ 0 &-1 \\ -1 &0 \end{bmatrix} จงหา A^t
วิธีทำ จะได้ว่า A^t =\begin{bmatrix}1 &0 &-1 \\ 2 &-1 &0 \end{bmatrix}
นอกจากนี้เมทริกซ์สลับเปลี่ยนก็ยังมีสมบัติอีกด้วย
สมบัติของเมทริกซ์สลับเปลี่ยน
- (A^t)^t=A
- (cA)^t=cA^t เมื่อ c เป็นจำนวนจริง
- (A+B)^t=A^t+B^t
- (AB)^t=B^tA^t
ในสมบัติข้อสุดท้าย ต้องอย่าลืมสลับที่ A กับ B ให้เป็นแบบในสมบัติที่พี่เขียนด้วย ไม่งั้นจะผิดได้น้า
พีชคณิตของเมทริกซ์
การบวกและการลบเมทริกซ์
ในหัวข้อนี้ พี่จะเริ่มพาน้อง ๆ มาดูการดำเนินการแบบง่าย ๆ กันก่อนนั่นคือการบวกและการลบเมทริกซ์ซึ่งจะเป็นตามบทนิยามต่อไปนี้
บทนิยาม
ให้ A=[a_{ij}]_{m\times n} และ B=[b_{ij}]_{m\times n} เป็นเมทริกซ์ที่มีขนาดเท่ากัน
ผลบวกของเมทริกซ์ A กับเมทริกซ์ B คือ [c_{ij}]_{m\times n} เมื่อ c_{ij}=a_{ij}+b_{ij}
สำหรับทุก i\in \left \{1, 2, 3, …, m \right \} และ j\in \left \{1, 2, 3, …, n \right \} เขียนแทน A บวก B ด้วย A+B
นั่นคือ [a_{ij}]_{m\times n}+[b_{ij}]_{m\times n}=[a_{ij}+b_{ij}]_{m\times n}
จากนิยามข้างต้นสามารถอธิบายแบบง่าย ๆ ภาษาชาวบ้านหนึ่ง ได้ว่า เมทริกซ์ขนาดเท่ากันในตำแหน่งเดียวกัน สามารถนำมาบวกหรือลบกันได้ นั่นก็คือเมทริกซ์ที่มีขนาดไม่เท่ากันจะนำมาบวกกันไม่ได้นั่นเอง
ตัวอย่างที่ 4
ให้ A=\begin{bmatrix}1 &0 &-1 \\ -2 &3 & 2\end{bmatrix}
และ B=\begin{bmatrix}0 & 1 &3 \\ 4 & -1 & -3\end{bmatrix} จงหา
1. A+B
วิธีทำ A+B=\begin{bmatrix}1 & 0 & -1 \\ -2 &3 & 2\end{bmatrix}+\begin{bmatrix}0&1 & 3 \\ 4 & -1 & -3\end{bmatrix}
=\begin{bmatrix}1+0 &0+1 &-1+3 \\ -2+4 &3+(-1) &2+(-3) \end{bmatrix}
= \begin{bmatrix}1 &1 &2 \\ 2 &2 &-1 \end{bmatrix}
2. A-B
วิธีทำ A-B=\begin{bmatrix}1 &0 &-1 \\ -2 &3 & 2\end{bmatrix}-\begin{bmatrix}0 & 1 &3 \\ 4 & -1 & -3\end{bmatrix}
=\begin{bmatrix}1-0 &0-1 &-1-3 \\ -2-4 &3-(-1) &2-(-3) \end{bmatrix}
= \begin{bmatrix}1 &-1 &-4 \\ -6 &4 &5 \end{bmatrix}
การคูณเมทริกซ์ด้วยจำนวนจริง
การคูณเมทริกซ์ด้วยจำนวนจริงก็ไม่ยากเลย ขั้นตอนการทำไม่ซับซ้อน ก่อนอื่นไปพิจารณาบทนิยามต่อไปนี้กัน
บทนิยาม
ให้ A=[a_{ij}]_{m\times n} และ c เป็นจำนวนจริง
ผลคูณของ c กับเมทริกซ์ A คือ เมทริกซ์ [b_{ij}]_{m\times n} เมื่อ b_{ij}=ca_{ij}
สำหรับทุก i\in \left \{1, 2, 3, …, m \right \} และ j\in \left \{1, 2, 3, …, n \right \}
เขียนแทนผลคูณของ c กับเมทริกซ์ A ด้วย cA
จะได้ว่า c[a_{ij}]_{m\times n}=[ca_{ij}]_{m\times n}
จากบทนิยามข้างบนนี้ เราสามารถทำความเข้าใจการคูณเมทริกซ์ด้วยจำนวนจริงได้แบบสั้น ๆ ดังนี้
ให้นำจำนวนจริงนั้น คูณสมาชิกทุกตัวในเมทริกซ์
ตัวอย่างที่ 5 ให้ A=\begin{bmatrix}1 & 2\\ 0 & -1\end{bmatrix} จงหา -5A
วิธีทำ -5A=\begin{bmatrix}-5\times 1 & -5\times 2\\ -5\times 0 & (-5)\times (-1)\end{bmatrix} =\begin{bmatrix}-5 & -10\\ 0 & 5\end{bmatrix}
การคูณเมทริกซ์ด้วยเมทริกซ์
น้อง ๆ คนไหนที่เคยเรียนบทเมทริกซ์แล้ว มาย้อนอ่านบทความนี้ก็จะรู้ว่าส่วนใหญ่เราจะมองว่าการคูณเมทริกซ์ด้วยเมทริกซ์มันทำความเข้าใจได้ยาก แต่น้อง ๆ คนไหนที่เพิ่งมาทำความรู้จักกับบทเมทริกซ์ด้วยกันตรงนี้ก็อย่าเพิ่งตกใจไปนะ การคูณเมทริกซ์ด้วยเมทริกซ์มันซับซ้อนกว่าหัวข้อที่ผ่านมาก็จริง แต่เราทำได้แน่นอนน แค่ต้องเพิ่มความรอบคอบในการคิดคำนวณเท่านั้นเอง การคูณเมทริกซ์ด้วยเมทริกซ์จะเป็นอย่างไร มาเริ่มดูที่บทนิยามกันก่อนเลย
บทนิยาม
ให้ A=[a_{ij}]_{m\times n} และ B=[b_{ij}]_{p\times q}
ผลคูณของเมทริกซ์ A และ B เขียนแทนด้วย AB จะนิยามได้ ก็ต่อเมื่อ n=p และเมทริกซ์ผลคูณ AB จะมีขนาด m\times q ซึ่งมีสมาชิกในแถวที่ i และหลักที่ j เป็น
a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}
สำหรับทุก i\in \left \{1, 2, 3, …, m \right \} และ j\in \left \{1, 2, 3, …, q \right \}
เพื่อให้เราทำความเข้าใจตามบทนิยามกันง่ายขึ้น ลองมาแบ่งวิธีการ คูณเมทริกซ์ด้วยเมทริกซ์จากนิยามข้างต้นแบบเป็นขั้นตอน 2 ขั้นตอนดังต่อไปนี้กัน
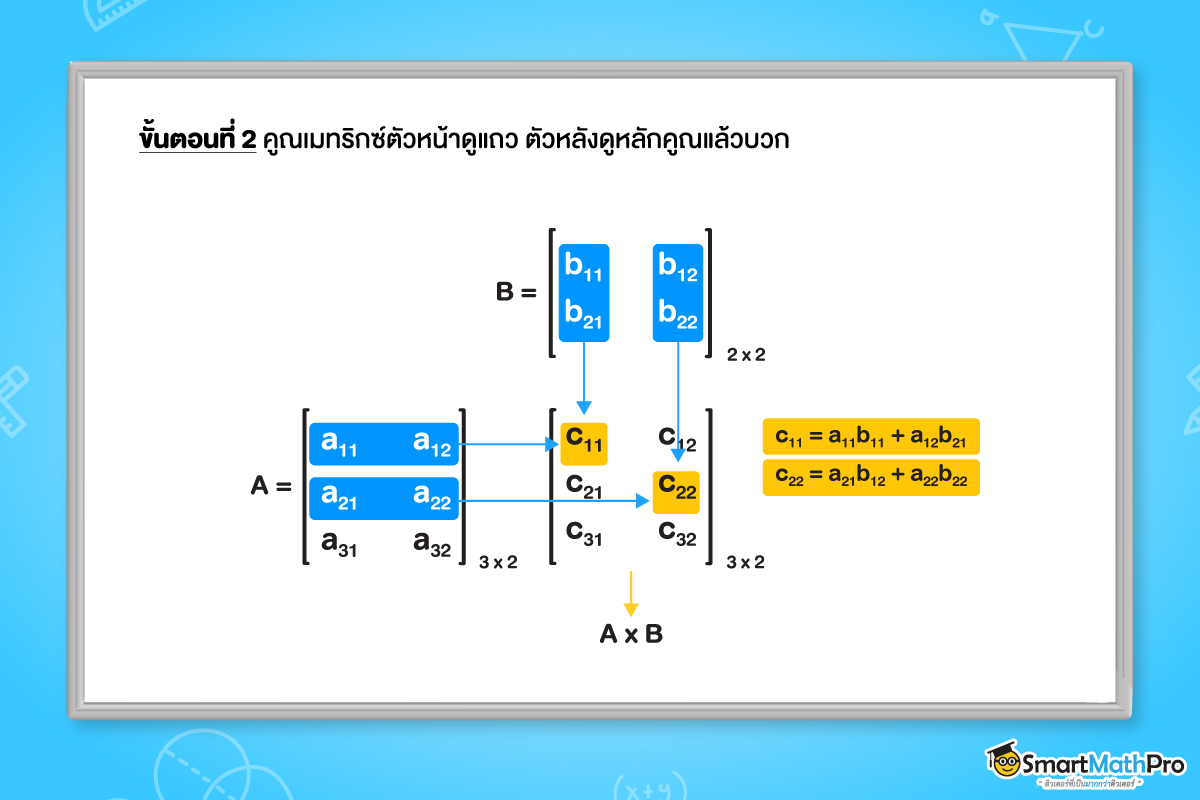
สังเกตได้ว่า ถ้าเราต้องการหาผลคูณของสมาชิกที่อยู่ในแถวที่ 1 และหลักที่ 1 นั่นคือ c_{11} จะต้องนำสมาชิกในแถวที่ 1 ของเมทริกซ์ A มาดำเนินการกับสมาชิกในหลักที่ 1 ของเมทริกซ์ B
ในทำนองเดียวกัน ถ้าเราอยากหาผลคูณของสมาชิกที่อยู่ในแถวที่ 2 หลักที่ 1 นั่นคือ c_{21} จะต้องนำสมาชิกในแถวที่ 2 ของเมทริกซ์ A มาดำเนินการกับสมาชิกในหลักที่ 1 ของเมทริกซ์ B
ตัวอย่างที่ 6 กำหนดให้ A=\begin{bmatrix}2 & 1\\ -1 & 0\end{bmatrix} และ B=\begin{bmatrix}0 & -1\\ 3 & 1\end{bmatrix} จงหา AB
วิธีทำ
ขั้นตอนที่ 1 ตรวจสอบว่าเมทริกซ์คูณกันได้หรือไม่
เมทริกซ์ A มีมิติเป็น 2\times 2 และเมทริกซ์ B มีมิติเป็น 2\times 2
ดังนั้นสามารถนำ A มาคูณกับ B ได้ โดยจะได้เมทริกซ์ AB ซึ่งเป็นคำตอบจะมีมิติเป็น 2\times 2
ขั้นตอนที่ 2 คูณเมทริกซ์
AB=\begin{bmatrix}(2)(0)+(1)(3) &(2)(-1)+(1)(1) \\ (-1)(0)+(0)(3) &(-1)(-1)+(0)(1) \end{bmatrix}=\begin{bmatrix}3 &-1 \\ 0 & 1\end{bmatrix}
ตัวอย่างที่ 7 กำหนดให้ A=\begin{bmatrix}-1 &1 \\ 3 & 2\end{bmatrix} และ B=\begin{bmatrix}1 &0 \\ 0 & 1\end{bmatrix} จงหา AB
วิธีทำ
ขั้นตอนที่ 1 ตรวจสอบว่าเมทริกซ์คูณกันได้หรือไม่
เมทริกซ์ A มีมิติเป็น 2\times 2 และเมทริกซ์ B มีมิติเป็น 2\times 2
ดังนั้นสามารถนำ A มาคูณกับ B ได้ โดยจะได้เมทริกซ์ AB ซึ่งเป็นคำตอบจะมีมิติเป็น 2\times 2
ขั้นตอนที่ 2 คูณเมทริกซ์
AB=\begin{bmatrix}(-1)(1)+(1)(0) &(-1)(0)+(1)(1) \\ (3)(1)+(2)(0) &(3)(0)+(2)(1) \end{bmatrix}= \begin{bmatrix}-1 &1 \\ 3 & 2\end{bmatrix}
จากตัวอย่างข้างต้นจะเห็นว่าเมื่อเรานำเมทริกซ์ A ไปคูณกับเมทริกซ์ B จะได้เมทริกซ์ที่เป็นคำตอบออกมาเป็นเมทริกซ์ที่หน้าตาเหมือนเมทริกซ์ A เลย นั่นก็เพราะว่าเมทริกซ์ B ในตัวอย่างก่อนหน้านั้นเป็น “เมทริกซ์เอกลักษณ์” ไม่ว่าเราจะนำเมทริกซ์ใดมาคูณกับมันก็จะได้เมทริกซ์เดิมเสมอเลย
เมทริกซ์เอกลักษณ์
ดีเทอร์มิแนนต์ของเมทริกซ์
มาทำความรู้จักดีเทอร์มิแนนต์ของเมทริกซ์จากบทนิยามกันก่อน โดยที่สัญลักษณ์ที่เราจะใช้แทนดีเทอร์มิแนนต์ของเมทริกซ์ A ก็คือ \det(A) หรือ |A|
ดีเทอร์มิแนนต์ของเมทริกซ์ที่มีขนาด 2 x 2
บทนิยาม
ให้ A=\begin{bmatrix}a & b\\ c & d\end{bmatrix} จะได้ ดีเทอร์มิแนนต์ของ A คือ ad-bc
จากบทนิยามทั้งหมด เพื่อให้น้อง ๆ จำการหาดีเทอร์มิแนนต์ได้ง่ายขึ้น พี่มีเทคนิคการจำมาให้ด้วย การหาดีเทอร์มิแนนต์ของเมทริกซ์ที่มีมิติ 2\times 2 ก็คือให้เรามองว่ามันคือจำนวนจริงที่เกิดจากการนำสมาชิกที่อยู่ในแนวทแยงมาคูณกันและลบกันดังนี้
ตัวอย่างที่ 8 กำหนดให้ A=\begin{bmatrix}2 &-1 \\ 0 & 3\end{bmatrix} จงหาดีเทอร์มิแนนต์ของเมทริกซ์ A
วิธีทำ
\begin{vmatrix}2 &-1 \\ 0 & 3\end{vmatrix}=(2)(3)-(0)(-1)=6
ดีเทอร์มิแนนต์ของเมทริกซ์ที่มีขนาด 3x3
ดีเทอร์มิแนนต์ของเมทริกซ์ที่มีขนาด 3×3 จะค่อนข้างซับซ้อนขึ้นมามากกว่าการหาดีเทอร์มิแนนต์ของเมทริกซ์ขนาด 2×2 น้อง ๆ บางคนอาจรู้จักวิธีการหาดีเทอร์มิแนนต์ด้วยการ “กระจายตามแถว” แต่ในบทความนี้พี่จะขอกล่าวถึงวิธีต่อไปนี้ ซึ่งทำความเข้าใจได้ง่าย มีเพียง 2 ขั้นตอนในการหาดีเทอร์มิแนนต์เท่านั้น ลองไปดูกันเลย
ตัวอย่างที่ 9 กำหนดให้ A=\begin{bmatrix}1 &0 &-1 \\ 0 &1 &-2 \\ 3 &1 &1 \end{bmatrix} จงหาดีเทอร์มิแนนต์ของเมทริกซ์ A
วิธีทำ
det(A)=\begin{vmatrix}1 &0 &-1 \\ 0 &1 &-2 \\ 3 &1 &1 \end{vmatrix}\begin{matrix}1 &0 \\ 0 &1 \\ 3 &1 \end{matrix}
=\left [(1)(1)(1)+(0)(-2)(3)+(-1)(0)(1) \right ]-\left [ (3)(1)(-1)+(1)(-2)(1)+(1)(0)(0) \right ]
=(1+0+0)-(-3-2+0)
=1+5
=6
เมทริกซ์ผกผัน
ในหัวข้อนี้จะมาศึกษาเกี่ยวกับเมทริกซ์ผกผันกัน พี่ขอพูดถึงความรู้เดิมของน้อง ๆ ในบทจำนวนจริงก่อน จากตัวผกผันการคูณของ 5 คือ \frac{1}{5} เนื่องจาก 5\cdot \frac{1}{5}=1 ซึ่ง 1 เป็นเอกลักษณ์การคูณ ในทำนองเดียวกัน หัวข้อนี้เราจะหาเมทริกซ์ซึ่งคูณกับเมทริกซ์ A แล้วได้ เมทริกซ์เอกลักษณ์ I_n กัน โดยเมทริกซ์ที่หามาได้เราจะเรียกว่าเมทริกซ์ผกผัน ตามนิยามต่อไปนี้
บทนิยาม
ให้ A เป็นเมทริกซ์ขนาด n\times n ถ้ามีเมทริกซ์ B ขนาด n\times n ซึ่ง
AB=BA=I_n
B คือเมทริกซ์ผกผันของเมทริกซ์ A และเขียนแทนด้วย A^{-1}
เมทริกซ์ที่สามารถหาเมทริกซ์ผกผัน จะนิยามเฉพาะเมทริกซ์จัตุรัสเท่านั้น และเมทริกซ์นั้น จะมีเมทริกซ์ผกผันเพียงเมทริกซ์เดียว โดยที่เราจะมีสูตรการหาเมทริกซ์ผกผันเป็นดังนี้
แล้วทุกเมทริกซ์จัตุรัสจะมีเมทริกซ์ผกผันทั้งหมดเลยไหมนะ ? คำตอบก็คือไม่ใช่น้าาาา สังเกตจากสูตรข้างต้นนี้ จะเห็นว่าการหาเมทริกซ์ผกผันของ A จะต้องถูกหารด้วย \det(A) นั่นหมายความว่าถ้า \det(A)=0 เมทริกซ์ A นั้นก็จะไม่มีเมทริกซ์ผกผันนั่นเอง ดังนั้นเวลาเราหาเมทริกซ์ผกผัน สามารถทดหา \det(A) เอาไว้ก่อนได้นะ เพราะถ้า \det(A)=0 เราจะได้ไม่ต้องทำต่อ แล้วตอบไปได้เลยว่าเมทริกซ์นี้ไม่มีเมทริกซ์ผกผัน
ตัวอย่างที่ 10 จงหาเมทริกซ์ผกผันของเมทริกซ์ต่อไปนี้ (ถ้ามี)
1. A=\begin{bmatrix}1 &2\\ 0 & -1\end{bmatrix}
วิธีทำ จะได้ \det(A)=(1)(-1)-(0)(2)=-1
ดังนั้น A^{-1}=\frac{1}{-1}\begin{bmatrix}-1 &-2 \\ 0 & 1\end{bmatrix}=\begin{bmatrix}\1 &2 \\ 0 & -1\end{bmatrix}
2. B=\begin{bmatrix}2 &-1 \\ -6 &3 \end{bmatrix}
วิธีทำ จะได้ \det(B)=(2)(3)-(-1)(-6)=6-6=0
ดังนั้นเมทริกซ์นี้ไม่มีเมทริกซ์ผกผัน
ระบบสมการเชิงเส้น
ในระดับชั้น ม.ต้น น้อง ๆ เคยแก้ระบบสมการเพื่อหาคำตอบมาแล้วซึ่งทำได้หลายวิธี การใช้เมทริกซ์ก็เป็นอีกวิธีหนึ่งที่จะช่วยให้เราหาคำตอบของระบบสมการได้ ไม่ว่าระบบสมการที่ง่าย ๆ หรือซับซ้อนเราก็สามารถนำความรู้เรื่องเมทริกซ์มาช่วยหาคำตอบได้นะ
เราสามารถนำวิธีการใช้เมทริกซ์เพื่อหาคำตอบของระบบสมการที่มีกี่สมการ กี่ตัวแปรก็ได้ แต่ในบทนี้จะเน้นเฉพาะระบบสมการเชิงเส้นที่มี 2 สมการ 2 ตัวแปร และระบบสมการเชิงเส้นที่มี 3 สมการ 3 ตัวแปรเท่านั้น
พี่จะพาน้อง ๆ มาพิจารณาการแก้สมการเมทริกซ์ 2 วิธีดังต่อไปนี้เลย
วิธีที่ 1 ใช้ตัวผกผันของเมทริกซ์ (วิธีย้ายข้าง)
ขั้นตอนที่ 1 เขียนระบบสมการให้อยู่ในรูปเมทริกซ์ AX=B
เช่น จากระบบสมการ
x+y=-1
2x-y=4
จะได้ ระบบสมการในรูปเมทริกซ์ AX=B
\begin{bmatrix}1 &1 \\ 2 &-1 \end{bmatrix}\begin{bmatrix}x\\y \end{bmatrix}=\begin{bmatrix}-1\\4\end{bmatrix}
ขั้นตอนที่ 2 หาเมทริกซ์ผกผัน ย้ายข้าง แก้สมการ
ระวัง ! ถ้าคูณเมทริกซ์เข้าไปที่ฝั่งซ้าย อีกข้างหนึ่งของสมการ ต้องคูณฝั่งซ้ายเช่นเดียวกัน ไม่สามารถคูณเข้าไปฝั่งขวาได้ เพราะเมทริกซ์ไม่มีสมบัติสลับที่การคูณ !
AX=B
A^{-1}AX=A^{-1}B
IX=A^{-1}B
X=A^{-1}B
ตัวอย่างที่ 11 จงหาคำตอบของระบบสมการ
x+y=-1
2x-y=4
วิธีทำ ให้ A=\begin{bmatrix}1 &1 \\ 2 &-1 \end{bmatrix} , X=\begin{bmatrix}x\\y \end{bmatrix} และ B=\begin{bmatrix}-1\\4\end{bmatrix}
เขียนระบบสมการให้อยู่ในรูปเมทริกซ์ AX=B ได้ดังนี้
\begin{bmatrix}1 &1 \\ 2 &-1 \end{bmatrix}\begin{bmatrix}x\\y \end{bmatrix}=\begin{bmatrix}-1\\4\end{bmatrix}
หาเมทริกซ์ผกผันของ A จะได้
A^{-1}=\frac{1}{1(-1)-2(1)}\begin{bmatrix}-1 &-1 \\ -2 &1 \end{bmatrix}
=\frac{1}{-3}\begin{bmatrix}-1 & -1\\ -2 &1 \end{bmatrix}
=\begin{bmatrix}\frac{1}{3} &\frac{1}{3} \\ \frac{2}{3} & -\frac{1}{3}\end{bmatrix}
เนื่องจาก X=A^{-1}B
ดังนั้น \begin{bmatrix}x\\y \end{bmatrix}=\begin{bmatrix}\frac{1}{3} &\frac{1}{3} \\ \frac{2}{3} & -\frac{1}{3}\end{bmatrix} \begin{bmatrix}-1\\4 \end{bmatrix}
=\begin{bmatrix}-\frac{1}{3}+\frac{4}{3}\\ -\frac{2}{3}-\frac{4}{3}\end{bmatrix}=\begin{bmatrix}1\\ -2\end{bmatrix}
นั่นคือ x=1 และ y=-2
ดังนั้น (1, -2) เป็นคำตอบของระบบสมการ
วิธีที่ 2 ใช้เมทริกซ์แต่งเติม
ขั้นตอนที่ 1 เขียนระบบสมการให้อยู่ในรูปเมทริกซ์แต่งเติม
จาก AX=B เขียนให้อยู่ในรูป [A|B]
ขั้นตอนที่ 2 ดำเนินการตามแถวโดยแปลงด้านซ้ายให้เป็นเมทริกซ์เอกลักษณ์ซึ่งการดำเนินการตามแถวทำได้ 3 แบบ ดังนี้
- R_i\leftrightarrow R_j
สลับแถวที่ i กับแถวที่ j ของเมทริกซ์ - cR_i
คูณสมาชิกในแถวที่ i ด้วยค่าคงตัว c ซึ่ง c\neq 0 - cR_i+R_j
คูณสมาชิกในแถวที่ i ด้วยค่าคงตัว c ซึ่ง c\neq 0 แล้วนำไปบวกกับสมาชิกในแถวที่ j เมื่อ i\neq j (แทนผลลัพธ์นี้ในแถว j)
ตัวอย่างที่ 12 จงหาคำตอบของระบบสมการเชิงเส้นต่อไปนี้
y-3z=-5
x+2z=4
2z=6
วิธีทำ
\left[ \begin{array}{rrr|r} 0 & 1 & -3 & -5 \\ 1 & 0 & 2 & 4 \\ 0 & 0 & 2 & 6 \end{array} \right] \sim \left[ \begin{array}{rrr|r} 1 & 0 & 2 & 4 \\ 0 & 1 & -3 & -5 \\ 0 & 0 & 2 & 6 \end{array} \right] R_2\leftrightarrow R_1
\sim \left[ \begin{array}{rrr|r} 1 & 0 & 2 & 4 \\ 0 & 1 & -3 & -5 \\ 0 & 0 & 1 & 3 \end{array} \right] \frac{1}{2}R_3
\sim \left[ \begin{array}{rrr|r} 1 & 0 & 2 & 4 \\ 0 & 1 & 0 & 4 \\ 0 & 0 & 1 & 3 \end{array} \right] 3R_3+R_2
\sim \left[ \begin{array}{rrr|r} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 4 \\ 0 & 0 & 1 & 3 \end{array} \right] -2R_3+R_1
ดังนั้น x=-2, y=4 และ z=3
ดูคลิปติวฟรี เมทริกซ์ ม.5
ดูคลิปติวฟรีอื่น ๆ ได้ที่ YouTube : SmartMathPro
ถึงแม้ว่าเนื้อหาคณิต ม.ปลาย จะยากขึ้นเรื่อย ๆ แต่ถ้าเราทบทวนบ่อย ๆ ก็จะช่วยเสริมพื้นฐานให้แข็งแรงแทำให้สามารถเรียนคณิต ม.ปลายบทต่อ ๆ ไปได้แบบเข้าใจมากขึ้น นอกจากนี้การมีพื้นฐานคณิตม.ปลายที่ดี ก็จะช่วยต่อยอดในการสอบเข้ามหาลัยฯ ได้ด้วยน้าาา โดยหลังจากทบทวนเนื้อหาแล้วพี่ก็แนะนำให้ฝึกโจทย์ด้วย จะได้เข้าใจมากขึ้น ซึ่งน้อง ๆ สามารถดาวน์โหลดแบบฝึกหัดเมทริกซ์ ม.5 ที่พี่เตรียมมาให้นี้ไปฝึกทำกันได้เลยย > <
แต่ถ้าใครรู้สึกว่าการทำโจทย์หรืออ่านเองยังไม่ทำให้เข้าใจเนื้อหาได้ดี อยากได้คนช่วยไกด์ให้ พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
คณิตศาสตร์ ม.5 เทอม 1 และเทอม 2 เรียนอะไรบ้าง ? สรุปครบทั้งคณิตพื้นฐานและเพิ่มเติม
ตรีโกณมิติ ม.5 สรุปพร้อมแจกโจทย์และสูตรจัดเต็ม !!
เวกเตอร์ ม.5 สรุปทุกเนื้อหา พร้อมโจทย์และวิธีทำที่ทุกคนห้ามพลาด!
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
