มีน้อง ๆ คนไหนรู้จักหรือเคยได้ยินเกี่ยวกับ แคลคูลัส บ้างงง พี่เชื่อว่าน้อง ๆ ที่กำลังเรียนอยู่ในระดับชั้น ม.6 น่าจะพอรู้กันมาบ้างแล้ว เพราะเรื่องนี้เป็นหนึ่งในบทเรียนของคณิตศาสตร์ ม.6 ที่น้อง ๆ จะได้เรียนกันตั้งแต่เทอม 1 นี่เองง
ซึ่งความพิเศษของบทนี้คือเป็นการเรียนแคลคูลัสเบื้องต้นเพื่อเอาไปต่อยอดกับบทเรียนแคลคูลัสในระดับมหาลัยฯ ได้เลย
ดังนั้นน้อง ๆ คนไหนที่มีแพลนจะเรียนคณะที่ใช้แคลคูลัสเป็นพื้นฐาน รวมถึงน้อง ๆ ที่อยากเตรียมพร้อมและเก็บเกรด 4
ที่โรงเรียน ห้ามพลาดกับสรุปเนื้อหาที่พี่เอามาฝากวันนี้เลย เพราะท้ายบทความพี่มีแจกข้อสอบแคลคูลัสให้ไปฝึกทำพร้อมคลิปติวฟรีเสริมความเข้าใจด้วย ใครพร้อมแล้วก็เลื่อนลงไปดูกันนน
ลิมิตและความต่อเนื่อง
ลิมิตของฟังก์ชัน
บทนิยาม
ถ้าค่าของฟังก์ชัน f(x) เข้าใกล้จำนวนจริง L เมื่อ x เข้าใกล้ a แล้วจะเรียก L ว่าลิมิตของฟังก์ชัน f ที่ a โดยใช้สัญลักษณ์ \lim_{x \to a}f(x)=L
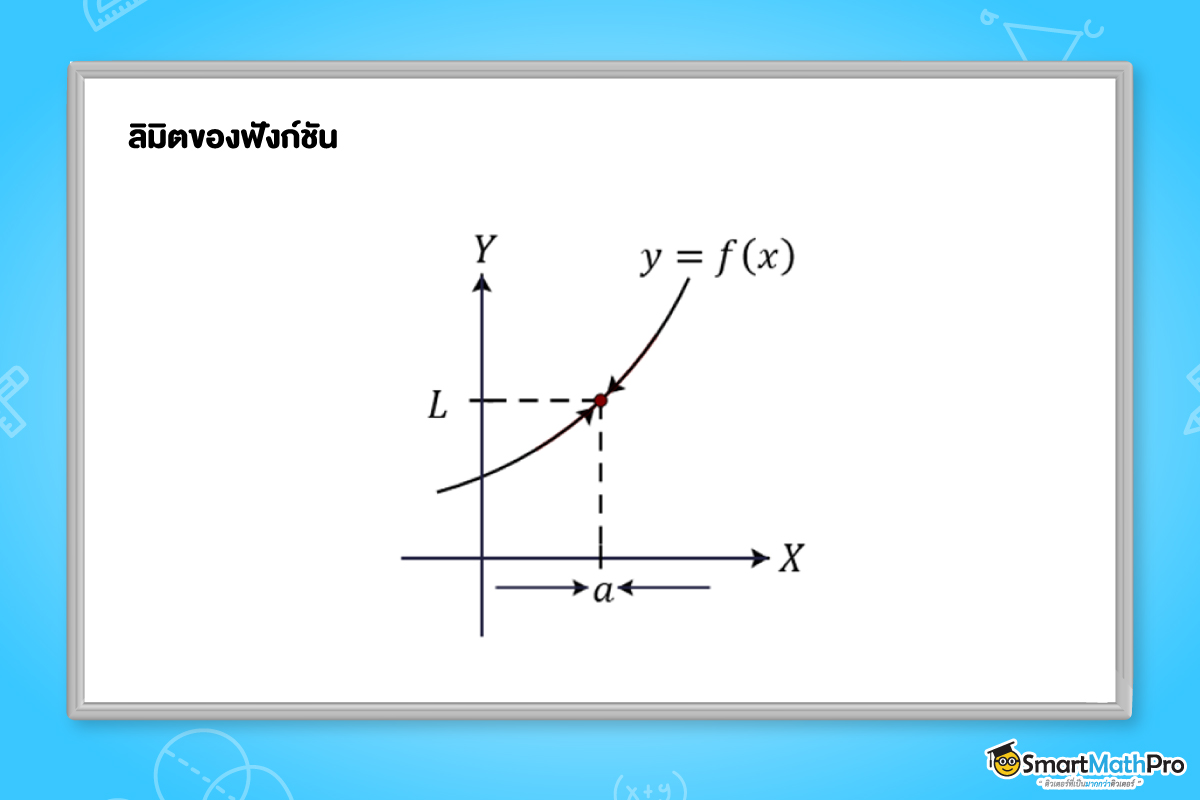
จากรูปจะเห็นได้ว่า ตำแหน่ง x=a สามารถเข้าใกล้ได้ทั้งสองด้าน คือซ้ายและขวา
• เมื่อ x เข้าใกล้ a ทางด้านซ้าย เขียนแทนด้วย x\to a^{-}
ลิมิตซ้ายของ f ที่ a เขียนแทนด้วย \lim_{x\to a^{-} }f(x)
• เมื่อ x เข้าใกล้ a ทางด้านขวา เขียนแทนด้วย x\to a^{+}
ลิมิตขวาของ f ที่ a เขียนแทนด้วย \lim_{x\to a^{+} }f(x)
ในกรณีที่ \lim_{x\to a^{-} }f(x)=\lim_{x\to a^{+} }f(x)=L เราจะสามารถสรุปได้ว่า \lim_{x\to a}f(x)=L
และในกรณีที่ \lim_{x\to a^{-} }f(x)\neq \lim_{x\to a^{+} }f(x) จะได้ว่า
f ไม่มีลิมิตที่ a หรือ \lim_{x\to a}f(x) ไม่มีค่านั่นเอง
ยิ่งไปกว่านั้น \lim_{x\to a}f(x)=L ไม่จำเป็นว่า f(a)=L เสมอไป
เราจะเห็นว่าการวาดกราฟเป็นวิธีพื้นฐานที่สามารถใช้หาลิมิตของฟังก์ชันได้
ทฤษฎีบทเกี่ยวกับลิมิตของฟังก์ชัน
ถ้า \lim_{x\to a}f(x)=L และ \lim_{x\to a}g(x)=M โดยที่ a เป็นจำนวนจริงแล้ว
• \lim_{x\to a}c=c เมื่อ c เป็นค่าคงตัวใด ๆ
• \lim_{x\to a}x^{n}=a^{n} เมื่อ n\in \mathbb{N}
• \lim_{x\to a}cf(x)=cL เมื่อ c เป็นค่าคงตัวใด ๆ
• \lim_{x\to a}(f(x)+g(x))=L+M
• \lim_{x\to a}(f(x)-g(x))=L-M
• \lim_{x\to a}(f(x)\cdot g(x))=L\cdot M
• \lim_{x\to a}\left ( \frac{f(x)}{g(x)} \right )=\frac{L}{M} เมื่อ M\neq 0
• \lim_{x\to a}(f(x))^{n}=L^{n} เมื่อ n\in \mathbb{N}
• \lim_{x\to a}\sqrt[n]{f(x)}=\sqrt[n]{L} เมื่อ n\in \mathbb{N}-\left \{ 1 \right \},\sqrt[n]{f(x)}\in \mathbb{R} สำหรับ x ที่เข้าใกล้ a และ \sqrt[n]{L}\in \mathbb{R}
เทคนิคการหาลิมิต
ในการหาลิมิตของฟังก์ชัน f เมื่อ x เข้าใกล้ a กราฟของฟังก์ชันบางอย่างอาจจะมีความซับซ้อนมากจนเกินไป จึงทำให้วาดได้ยาก ดังนั้นนอกจากการวิเคราะห์โดยใช้การวาดกราฟของฟังก์ชัน f แล้วยังมีอีกวิธีคือการแทนค่า a ลงในฟังก์ชัน f หรือหาค่าของ f(a) นั่นเอง บางครั้งการหาลิมิตของฟังก์ชันด้วยวิธีดังกล่าวอาจมีปัญหาได้ เช่น ได้ค่าที่ตัวส่วนเป็น 0 หรือเกิด \frac{0}{0} น้อง ๆ สามารถใช้เทคนิคดังต่อไปนี้ในการแก้ปัญหาข้างต้นได้
- วิธีที่ 1 ใช้การแยกตัวประกอบ
ตัวอย่างที่ 1 จงหา \lim_{x\to 1}\frac{x-1}{x^{2}-1}
แนวคิด ลองใช้วิธีการแทนค่า จะได้ \frac{0}{0} แสดงว่า มีพจน์ที่ทำให้เกิด 0 ทั้งเศษและส่วน
เมื่อลองแยกตัวประกอบ จะได้ว่า
\lim_{x\to 1}\frac{x-1}{x^{2}-1}
=\lim_{x\to 1}\frac{x-1}{(x-1)(x+1)}
=\lim_{x\to 1}\frac{1}{x+1}
=\frac{1}{2}
- วิธีที่ 2 คูณด้วยคอนจูเกต
ตัวอย่างที่ 2 จงหา \lim_{x\to 1}\frac{\sqrt{x}-1}{x-1}
แนวคิด ลองใช้วิธีแทนค่า จะได้ \frac{0}{0} ในลักษณะแบบนี้ การแยกตัวประกอบอาจยากเกินไป
ใช้การคูณด้วยคอนจูเกตช่วย จะได้ว่า
\lim_{x\to 1}\frac{\sqrt{x}-1}{x-1}
\\=\lim_{x\to 1}\frac{\sqrt{x}-1}{x-1}\cdot \frac{\sqrt{x}+1}{\sqrt{x}+1}
\\=\lim_{x\to 1}\frac{x-1}{(x-1)(\sqrt{x}+1)}
\\=\lim_{x\to 1}\frac{1}{\sqrt{x}+1}
\\=\frac{1}{2}
ความต่อเนื่องของฟังก์ชัน
f เป็นฟังก์ชันต่อเนื่องที่ x=a ก็ต่อเมื่อ
• f(a) หาค่าได้ (a ต้องอยู่ในโดเมนของ f )
• \lim_{x\to a}f(x) มีค่า
• \lim_{x\to a}f(x)=f(a)
เราจะได้ว่า f เป็นฟังก์ชันต่อเนื่องที่ x=a ก็ต่อเมื่อ \lim_{x\to a^{-}}f(x)=\lim_{x\to a^{+}}f(x)=f(a)
ตัวอย่างที่ 3 กำหนดให้
f(x)=\left\{\begin{matrix}x^{2}+1,x\geq2
\\x+3,x<2
\end{matrix}\right.
จงพิจารณาว่าฟังก์ชัน f เป็นฟังก์ชันต่อเนื่องที่ x=2 หรือไม่
วิธีทำ เมื่อพิจารณาที่ x=2 จะต้องใช้ f(x)=x^{2}+1
จะได้ว่า f(2)=2^{2}+1=5
พิจารณา \lim_{x \to2^{-} }f(x) จะได้ว่า \lim_{x \to2^{-} }f(x)=\lim_{x \to2^{-} }(x+3)=2+3=5
พิจารณา \lim_{x \to2^{+} }f(x) จะได้ว่า \lim_{x \to2^{+} }f(x)=\lim_{x \to2^{+} }(x^{2}+1)=2^{2}+1=5
ดังนั้น \lim_{x \to2 }f(x)=5=f(2)
เพราะฉะนั้นฟังก์ชัน f เป็นฟังก์ชันต่อเนื่องที่ x=2
อนุพันธ์ของฟังก์ชัน
อัตราการเปลี่ยนแปลง
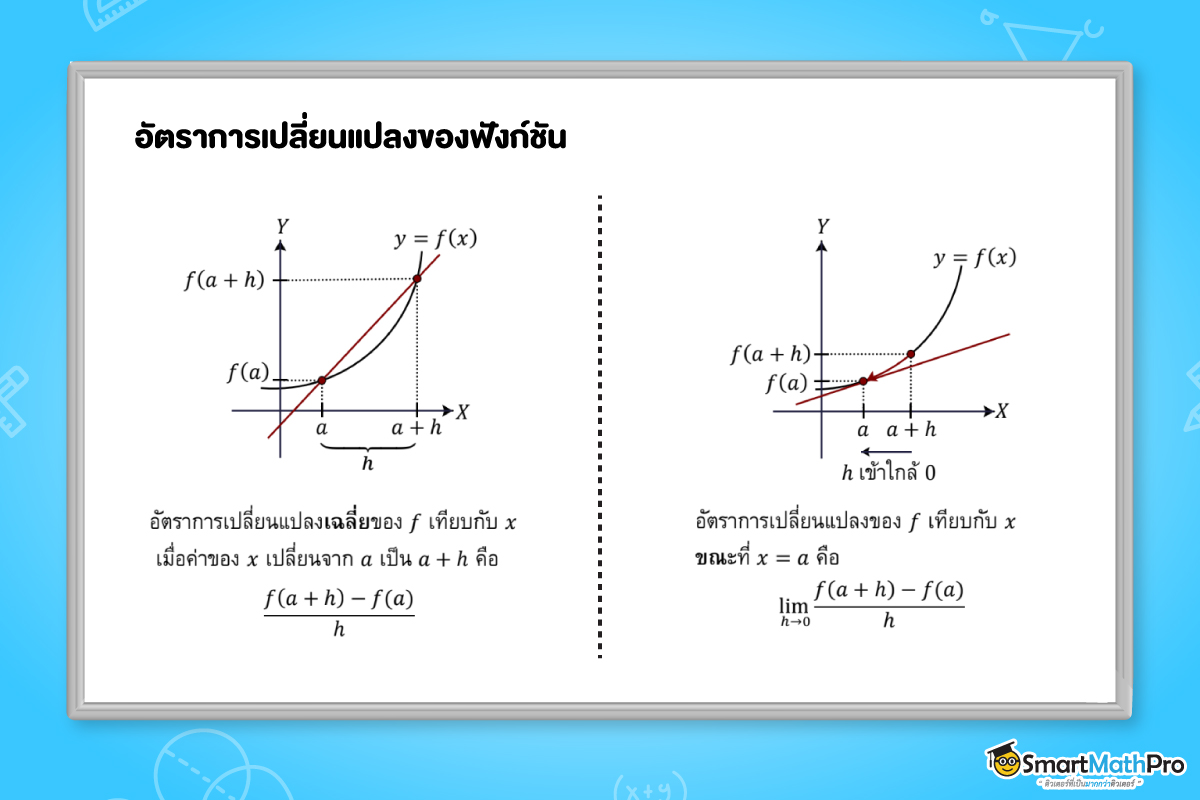
จากกราฟ จะเห็นว่า เมื่อ x=a จะได้ค่าของฟังก์ชันคือ f(a) และเมื่อ x=a+h จะได้ค่าของฟังก์ชันคือ f(a+h) จะได้ว่าเมื่อ x เปลี่ยนจาก a เป็น a+h ค่าของฟังก์ชันจะเปลี่ยนไป f(a+h)-f(a)
ดังนั้น อัตราการเปลี่ยนแปลงเฉลี่ยของ f เทียบกับ x เมื่อค่าของ x เปลี่ยนจาก a เป็น a+h
จะเท่ากับ \frac{f(a+h)-f(a)}{(a+h)-a}=\frac{f(a+h)-f(a)}{h}
น้อง ๆ ลองสังเกตจากกราฟ เมื่อค่า h ยิ่งเข้าใกล้ 0 ค่าของ a และค่าของ a+h จะมีความใกล้เคียงกันมากขึ้น
ดังนั้น เราจึงสามารถหาอัตราการเปลี่ยนแปลงของ f เทียบกับ x ขณะที่
x=a ได้จาก \lim_{h \to 0 }\frac{f(a+h)-f(a)}{h} นั่นเอง
บทนิยามของอนุพันธ์ของฟังก์ชัน
จากอัตราการเปลี่ยนแปลงของ f เทียบกับ x ขณะที่ x=a คือ \lim_{h \to 0 }\frac{f(a+h)-f(a)}{h} ถ้าลิมิตนี้หาค่าได้ เราจะเรียกว่าอนุพันธ์ของฟังก์ชัน f ที่ a ตามบทนิยามต่อไปนี้
ให้ f เป็นฟังก์ชัน อนุพันธ์ของฟังก์ชัน f ที่ x เขียนแทนด้วย f'(x) คือ
f'(x)=\lim_{h \to 0 }\frac{f(x+h)-f(x)}{h}
นอกจากสัญลักษณ์ f'(x) ถ้า f(x)=y แล้ว อนุพันธ์ของฟังก์ชัน f ที่ x ยังสามารถเขียนแทนด้วยสัญลักษณ์ \frac{dy}{dx}
การหาอนุพันธ์ของฟังก์ชันโดยใช้สูตร
สูตรการหาอนุพันธ์พื้นฐาน
กำหนดให้ a และ c เป็นจำนวนจริงใด ๆ
ถ้า f(x)=c แล้ว f'(x)=0
ถ้า f(x)=x^{a} แล้ว f'(x)=ax^{a-1}
(cf)'(x)=cf'(x)
(f\pm g)'(x)=f'(x)\pm g'(x)
จากสูตรการหาอนุพันธ์พื้นฐาน จะเห็นว่าการบวกและการลบ เราสามารถหาอนุพันธ์ทีละพจน์ได้ (การบวกและการลบกระจายได้) แต่การคูณและการหารไม่สามารถหาอนุพันธ์ทีละพจน์ได้ (การคูณและการหารกระจายไม่ได้น้า) ซึ่งการหาอนุพันธ์ผลคูณและผลหารมีสูตรเฉพาะ ดังนี้
สูตรการหาอนุพันธ์ผลคูณและผลหาร
• (fg)'(x)=f'(x)g(x)+f(x)g'(x)
• \left (\frac{f}{g} \right )'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{(g(x))^{2}} โดยที่ g(x)\neq 0
เพื่อให้เข้าใจมากขึ้น เราลองไปดูการหาอนุพันธ์ของฟังก์ชันโดยใช้สูตรผ่านตัวอย่างกัน
ตัวอย่างที่ 4 กำหนดให้ h(x)=(x^{2}+1)(3x-2) จงหา h'(x)
วิธีทำ h'(x)=(x^{2}+1)'(3x-2)+(x^{2}+1)(3x-2)′
=(2x+0)(3x-2)+(x^{2}+1)(3+0)
=(2x)(3x-2)+(x^{2}+1)(3)
=(6x^{2}-4x)+(3x^{2}+3)
=9x^{2}-4x+3
อนุพันธ์ของฟังก์ชันประกอบ
ฟังก์ชันประกอบ g\circ f ก็สามารถหาอนุพันธ์ได้ โดยเราจะเรียกวิธีการหานี้ว่า กฎลูกโซ่ ซึ่งเราสามารถหาอนุพันธ์ของฟังก์ชันประกอบได้จากสูตรนี้เลย
สูตรการหาอนุพันธ์ของฟังก์ชันประกอบ
(g\circ f )'(x)=g'(f(x))\cdot f'(x)
ตัวอย่างที่ 5 กำหนดให้ h(x)=(2x+1)^{5} จงหา h'(x)
วิธีทำ กำหนดให้ f(x)=2x+1 และ g(x)=x^5
จากสูตร จะได้ f(x)=2x+1
g(f(x))=(2x+1)^{5}
h'(x)=g'(f(x))\cdot f'(x)
=[(2x+1)^{5}]′ \cdot (2x+1)′
=5(2x+1)^{4}\cdot(2+0)
=5(2x+1)^{4}\cdot(2)
=10(2x+1)^{4}
เส้นสัมผัสเส้นโค้ง
ให้เส้นโค้ง y=f(x) และมีจุด P(a,f(a)) อยู่บนเส้นโค้ง
• ความชันของเส้นสัมผัส คือ f'(a)
• สมการเส้นสัมผัส หาได้จากสูตรสมการเส้นตรง y-y_{1}=m(x-x_{1}) ที่ m=f'(a) และผ่านจุด P(a,f(a))
y-f(a)=f'(a)(x-a)
ฟังก์ชันเพิ่มและฟังก์ชันลด
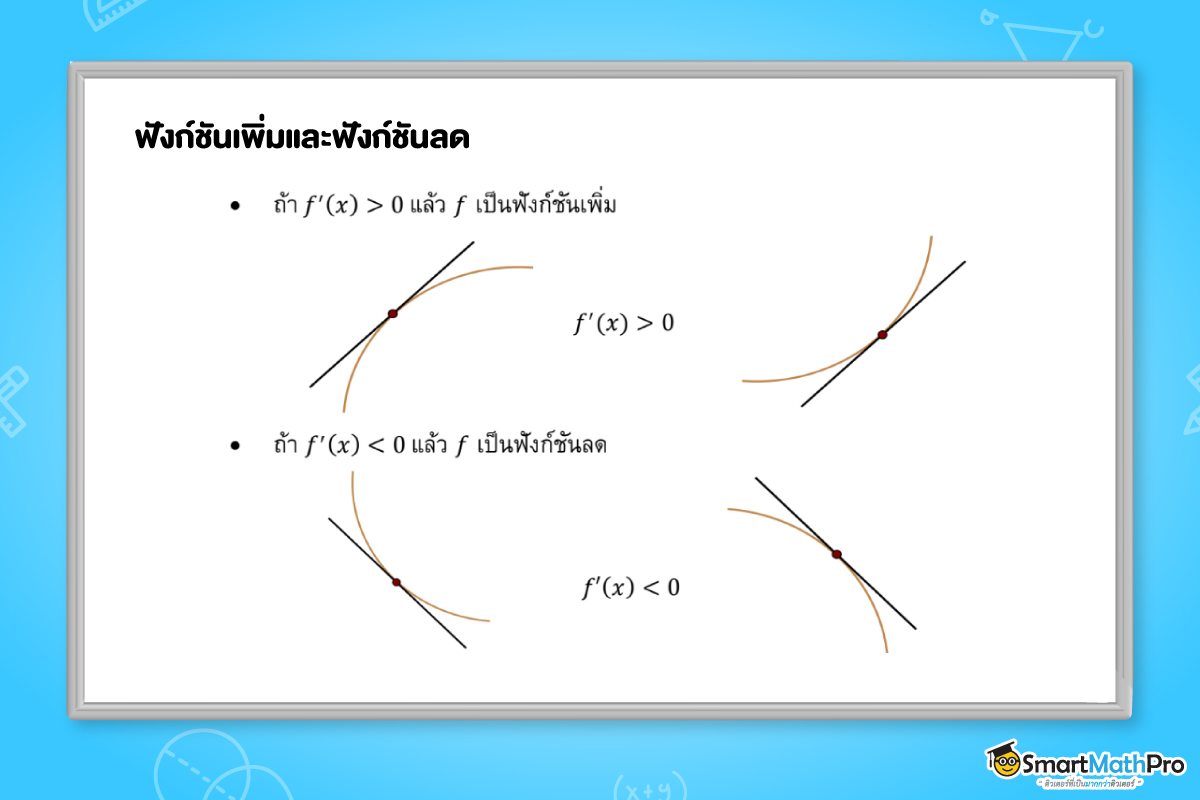
จากรูปข้างต้น สังเกตได้ว่า ถ้าความชันของเส้นสัมผัสเส้นโค้งมีค่าเป็นบวก (f'(x)>0) แล้ว f เป็นฟังก์ชันเพิ่ม และถ้าความชันของเส้นสัมผัสเส้นโค้งมีค่าเป็นลบ (f'(x)<0) แล้ว f เป็นฟังก์ชันลด นั่นเอง
จุดวิกฤต ค่าสูงสุดและค่าต่ำสุดของฟังก์ชัน
เราจะเรียก c ที่ทำให้ f'(c)=0 หรือ f'(c) ไม่มีค่า ว่า ค่าวิกฤต และเรียก (c,f(c)) ว่า จุดวิกฤต โดยในหลักสูตรม.ปลายนี้ เราจะพิจารณาแต่ f'(c)=0
ค่าสุดขีดสัมพัทธ์
วิธีการหาค่าสุดขีดสัมพัทธ์ มีขั้นตอนดังต่อไปนี้
ขั้นตอนที่ 1 หาค่าวิกฤตจากสมการ f'(x)=0
ขั้นตอนที่ 2 วาดเส้นจำนวนเพื่อหาค่าสูงสุด–ต่ำสุดสัมพัทธ์
- ถ้าเปลี่ยนจาก + เป็น – แสดงว่าเป็นค่าสูงสุดสัมพัทธ์
(ฟังก์ชันเพิ่มเปลี่ยนเป็นฟังก์ชันลด) - ถ้าเปลี่ยนจาก – เป็น + แสดงว่าเป็นค่าต่ำสุดสัมพัทธ์
(ฟังก์ชันลดเปลี่ยนเป็นฟังก์ชันเพิ่ม)
ขั้นตอนที่ 3 สรุปคำตอบ
ตัวอย่างที่ 6 จงหาจุดสูงสุดและจุดต่ำสุดสัมพัทธ์ของฟังก์ชัน f(x)=2x^{3}-3x^{2}-12x+3
ขั้นตอนที่ 1 หาค่าวิกฤตจากสมการ f'(x)=0
จาก f(x)=2x^{3}-3x^{2}-12x+3 \\f'(x)=6x^{2}-6x-12 \\=6(x^{2}-x-2) \\=6(x-2)(x+1)
ถ้า f'(x)=0 จะได้ 6(x-2)(x+1)=0
ดังนั้น x=-1,2
ขั้นตอนที่ 2 วาดเส้นจำนวนเพื่อหาตำแหน่งของค่าสูงสุด – ต่ำสุดสัมพัทธ์
ขั้นตอนที่ 3 สรุปคำตอบ
f(-1)=2(-1)^{3}-3(-1)^{2}-12(-1)+3=10
f(2)=2(2)^{3}-3(2)^{2}-12(2)+3=-17
ดังนั้น จุดสูงสุดสัมพัทธ์ของ f คือ (-1,10) และจุดต่ำสุดสัมพัทธ์ของ f คือ (2,-17)
ค่าสุดขีดสัมบูรณ์
วิธีการหาค่าสุดขีดสัมบูรณ์มีขั้นตอนดังต่อไปนี้
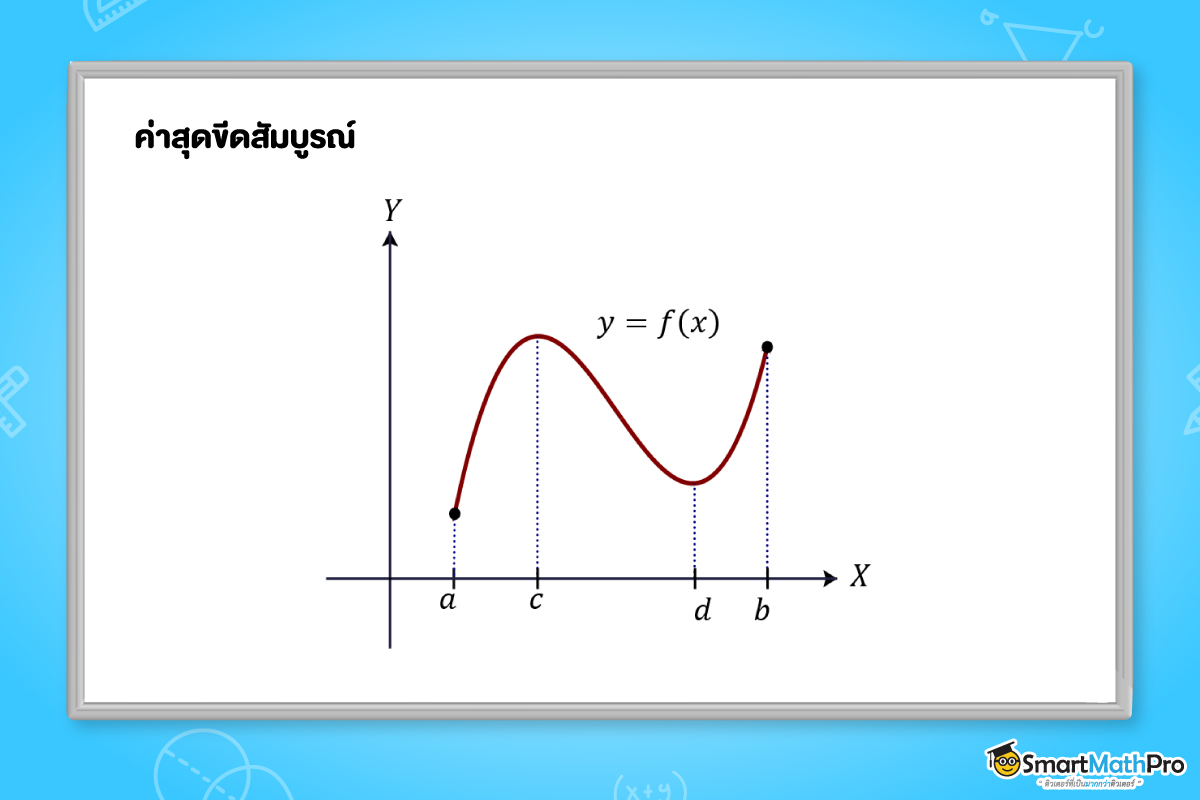
ขั้นตอนที่ 1 หาค่าวิกฤตจากสมการ f'(x)=0
ขั้นตอนที่ 2 เช็กช่วงว่า ค่า x ที่ได้จากขั้นตอนที่ 1 อยู่ในช่วง [a,b] หรือไม่ โดยเลือกเฉพาะค่าที่อยู่ในช่วง
ขั้นตอนที่ 3 นำขอบของช่วงนั่นก็คือ a และ b รวมไปถึงค่า x ที่ได้จากขั้นตอนที่ 2 มาแทนค่าในฟังก์ชันเริ่มต้นเพื่อหาค่าสุดขีดสัมบูรณ์
ขั้นตอนที่ 4 สรุปคำตอบ (ค่าที่มากที่สุดเป็นค่าสูงสุดสัมบูรณ์และค่าที่น้อยที่สุดเป็นค่าต่ำสุดสัมบูรณ์)
ตัวอย่างที่ 7
จงหาค่าสูงสุดและค่าต่ำสุดสัมบูรณ์ของฟังก์ชัน f(x)=x^{3}-3x+2 บนช่วงปิด [0,2]
ขั้นตอนที่ 1 หาค่าวิกฤตจากสมการ f'(x)=0
จาก f(x)=x^{3}-3x+2 \\f'(x)=3x^{2}-3 \\=3(x^{2}-1) \\=3(x+1)(x-1)
ถ้า f'(x)=0 จะได้ 3(x+1)(x-1)=0
ดังนั้น x=-1,1
ขั้นตอนที่ 2 เช็กช่วง
-1\notin [0,2] แสดงว่าจะพิจารณาที่ x=1เท่านั้น
ขั้นตอนที่ 3 นำขอบมาคิดด้วย
ขอบของ [0,2] คือ x=0,2
f(0)=(0)^{3}-3(0)+2=2
f(1)=(1)^{3}-3(1)+2=0 (น้อยสุด)
f(2)=(2)^{3}-3(2)+2=4 (มากสุด)
ขั้นตอนที่ 4 สรุปคำตอบ
ดังนั้น ค่าต่ำสุดสัมบูรณ์ของ f คือ 4 ที่ x=2 และค่าสูงสุดสัมบูรณ์ของ f คือ 0 ที่ x=1
อนุพันธ์อันดับสูง
จากหัวข้อที่แล้วเราได้เรียนรู้เรื่องการหาอนุพันธ์ไปแล้ว และถ้าเรายังสามารถนำฟังก์ชัน f'(x) มาหาอนุพันธ์ต่อได้อีก เราจะเรียกฟังก์ชันที่เป็นอนุพันธ์ของ f'(x) ว่าอนุพันธ์อันดับสูงนั่นเอง
บทนิยาม
ให้ f เป็นฟังก์ชันที่สามารถหาอนุพันธ์ได้ และอนุพันธ์ของฟังก์ชัน f ที่ x เป็นฟังก์ชันที่หาอนุพันธ์ได้ จะเรียกอนุพันธ์ของฟังก์ชัน f′ ที่ x ว่าอนุพันธ์อันดับที่ 2 ของฟังก์ชัน f ที่ x และเขียนแทนด้วย และเขียนแทนด้วย f″(x)
เราสามารถใช้สัญลักษณ์อื่น ๆ แทนอนุพันธ์อันดับที่ 2 ของ f ที่ x ได้อีก เช่น {y}″,\frac{d^{2}y}{dx^{2}} หรือ \frac{d^{2}}{dx^{2}}f(x)
ตัวอย่างที่ 8 กำหนดให้ f(x)=6x^{3}+5x^{2}+4x+3 จงหา f″(x)
วิธีทำ จาก f(x)=6x^{3}+5x^{2}+4x+3
จะได้ว่า f'(x)=18x^{2}+10x+4
ดังนั้น f″(x)=36x+10
ในทำนองเดียวกัน เราสามารถกล่าวถึงอนุพันธ์อันดับที่ 3 ของ f ที่ x ว่าเป็นอนุพันธ์ของอนุพันธ์อันดับที่ 2 กล่าวถึงอนุพันธ์อันดับที่ 4 ของ f ที่ x ว่าเป็นอนุพันธ์ของอนุพันธ์อันดับที่ 3 และ อนุพันธ์อันดับที่ n ของ f ที่ x ว่าเป็นอนุพันธ์ของอนุพันธ์อันดับที่ n-1
ปฏิยานุพันธ์ของฟังก์ชัน
หัวข้อก่อนหน้าเราได้ศึกษาเกี่ยวกับอนุพันธ์ของฟังก์ชันไปแล้ว ต่อไปเราจะศึกษากระบวนการที่กลับกัน นั่นคือการหาปฏิยานุพันธ์ของฟังก์ชัน เมื่อให้ f เป็นฟังก์ชัน เราจะหาฟังก์ชัน F ซึ่ง F'(x)=f(x) และจะเรียกฟังก์ชัน F ว่า ปฏิยานุพันธ์ของฟังก์ชัน f
เช่น F(x)=6x^{2}+5x เป็นปฏิยานุพันธ์ของ f(x)=12x+5
แต่ปฏิยานุพันธ์ของ f ไม่ได้มีเพียงฟังก์ชันเดียวนะ ลองสังเกตฟังก์ชันต่อไปนี้ดู
F_{1}(x)=6x^{2}+5x
\\F_{2}(x)=6x^{2}+5x+1
\\F_{3}(x)=6x^{2}+5x-2
น้อง ๆ น่าจะพอรู้แล้วว่าฟังก์ชันทั้งสามที่พี่ยกตัวอย่างมาล้วนเป็นปฏิยานุพันธ์ของฟังก์ชัน f ทั้งหมดเลย เพราะF'(x)=f(x) นั่นเอง
บทนิยาม
ให้ f เป็นฟังก์ชัน ถ้า F เป็นฟังก์ชันซึ่ง F'(x)=f(x) สำหรับทุก x ที่อยู่ในโดเมนของ f
แล้วจะเรียก F ว่าเป็นปฏิยานุพันธ์หนึ่งของ f
จากตัวอย่างข้างต้น น้อง ๆ จะเห็นว่า ฟังก์ชันใด ๆ ที่อยู่ในรูป F(x)=6x^{2}+5x+c เมื่อ c เป็นค่าคงตัว จะเป็นปฏิยานุพันธ์ของ f(x)=12x+5 ทั้งหมดเลย
เราจะเขียนรูปทั่วไปของปฏิยานุพันธ์ของฟังก์ชัน f ด้วยสัญลักษณ์ \int f(x)dx เรียกว่า ปริพันธ์ไม่จำกัดเขตของฟังก์ชัน f เทียบกับตัวแปร x
การหาปริพันธ์ไม่จำกัดเขต
สูตรสำหรับหาปริพันธ์ไม่จำกัดเขตของบางฟังก์ชัน
กำหนดให้ a, k และ c เป็นจำนวนจริง
• \int kdx=kx+c
• \int x^{a}dx=\frac{x^{a+1}}{a+1}+c เมื่อ a\neq 1
• \int kf(x)dx=k\int f(x)dx
• \int (f(x)\pm g(x))dx=\int f(x)dx\pm \int g(x)dx
การหาปริพันธ์จำกัดเขต
ทฤษฎีบทหลักมูลของแคลคูลัส
กำหนดให้ f เป็นฟังก์ชันต่อเนื่องบน [a,b] ถ้าF เป็นปฏิยานุพันธ์ของฟังก์ชัน f แล้ว
\int_{a}^{b}f(x)dx=F(x)\mid_{a}^{b}=F(b)-F(a)
ตัวอย่างที่ 9 จงหา \int_{0}^{1}(3x^{2}+2x+1)dx
วิธีทำ
จาก f(x)=3x^{2}+2x+1 เป็นฟังก์ชันต่อเนื่องบนช่วง [0,1]
และปฏิยานุพันธ์ของ f(x)=3x^{2}+2x+1
คือ F(x)=\frac{3x^{3}}{3}+\frac{2x^{2}}{2}+\frac{x^{1}}{1}+c=x^{3}+x^{2}+x+c เมื่อ c เป็นค่าคงตัว
จะได้ว่า
\int_{0}^{1}(3x^{2}+2x+1)dx
\\=(x^{3}+x^{2}+x+c)\mid _{0}^{1}
\\=(1^{3}+1^{2}+1+c)-(0^{3}+0^{2}+0+c)
\\=(3+c)-(0+c)
\\=3
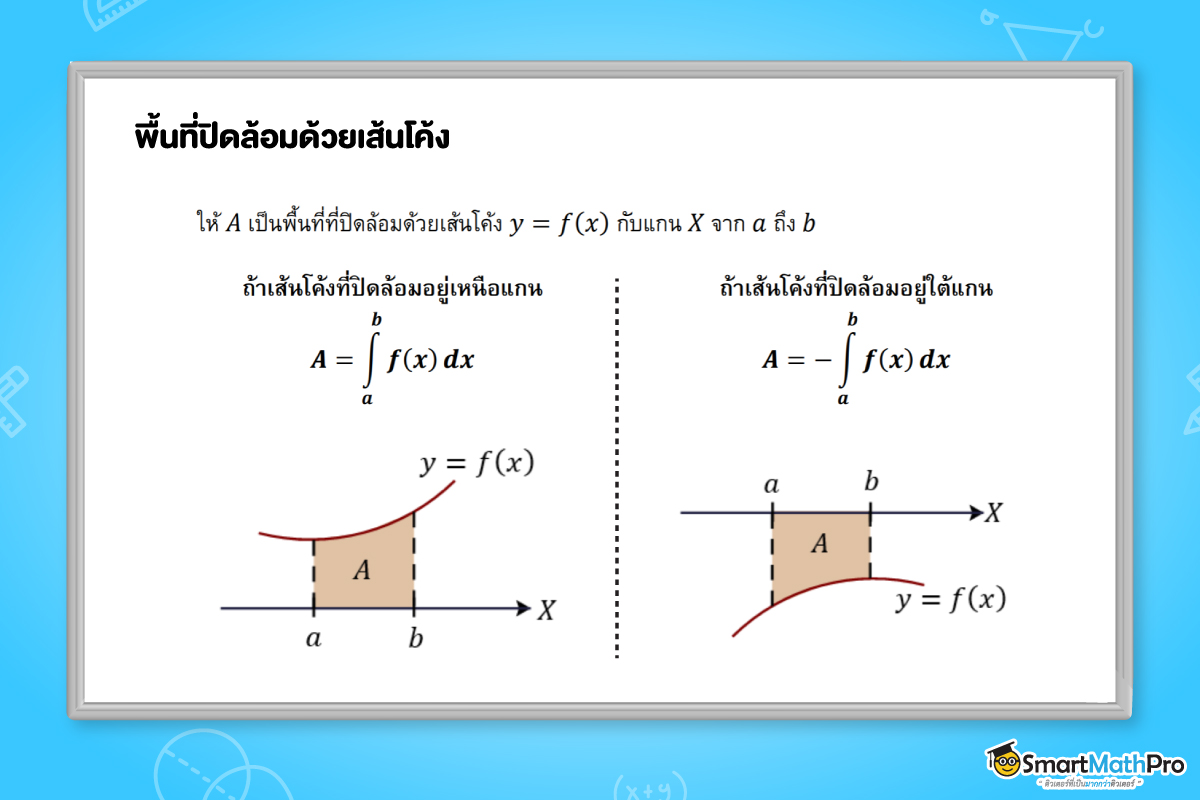
พื้นที่ปิดล้อมด้วยเส้นโค้ง
จากหัวข้อก่อนหน้า เราได้ศึกษาเกี่ยวกับปริพันธ์จำกัดเขตไปแล้ว โดยการเขียนปริพันธ์จำกัดเขตในรูป
\int_{a}^{b}f(x)dx คือพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y=f(x) จาก a
ถึง b เมื่อ f(x)\geq 0 สำหรับทุก x\in[a,b]
ในหัวข้อนี้เราจะศึกษาวิธีการหาพื้นที่ที่ปิดล้อมด้วยเส้นโค้ง y=f(x) กับแกน X โดยแยกพิจารณาบนช่วงที่ f(x)\geq 0 (เส้นโค้งที่ปิดล้อมอยู่เหนือแกน X) และ
f(x)\leq0 (เส้นโค้งที่ปิดล้อมอยู่ใต้แกน X) ดังนี้
เช่น
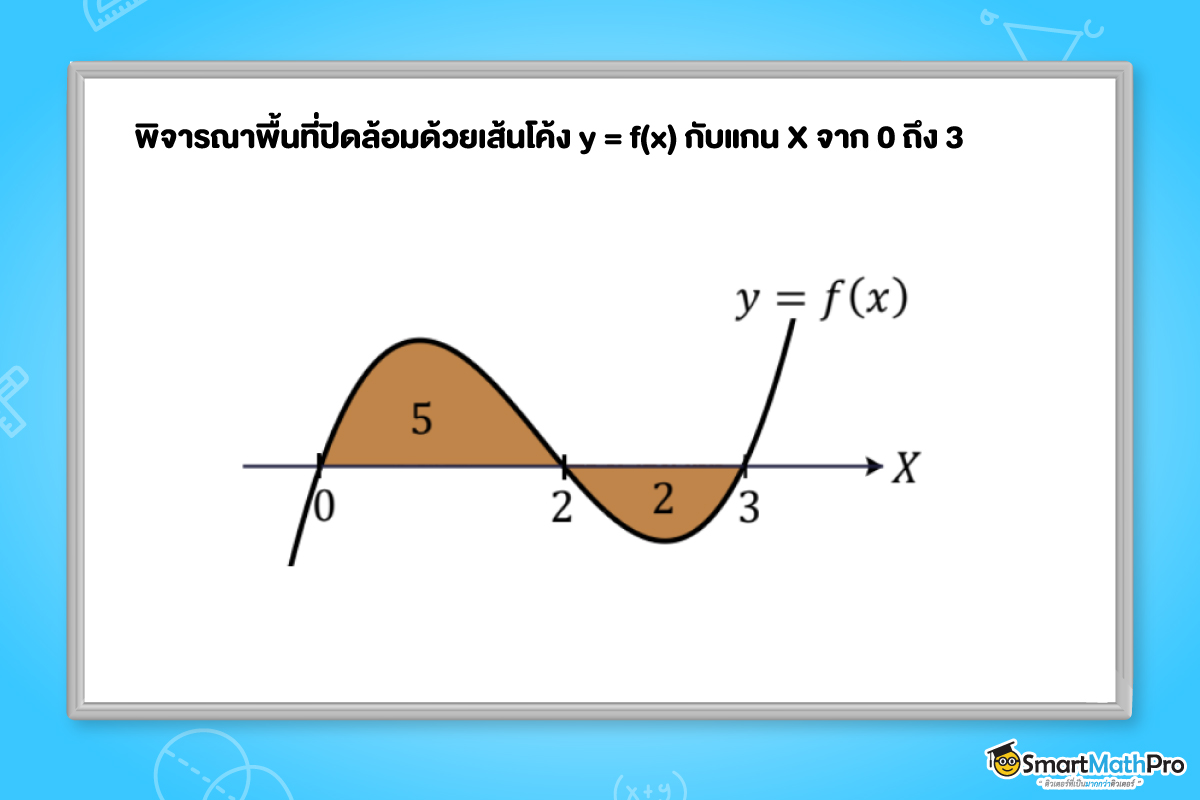
พื้นที่ใต้กราฟในช่วง 0 ถึง 2 เท่ากับ 5 และ \int_{0}^{2}f(x)dx=5
พื้นที่ใต้กราฟในช่วง 2 ถึง 3 เท่ากับ 2 แต่ \int_{2}^{3}f(x)dx=-2
ดังนั้น พื้นที่ใต้กราฟกับค่าอินทิเกรตไม่จำเป็นต้องเท่ากันเสมอไป
Q&A ตอบคำถามเกี่ยวกับแคลคูลัส
บทนี้เป็นบทที่หลายคนคิดว่ายาก แต่ถ้าน้อง ๆ มีพื้นฐานความรู้จากบทจำนวนจริง บทความสัมพันธ์และฟังก์ชัน (จริง ๆ แล้วบทแคลคูลัสเหมือนเป็นภาคต่อของบทนี้เลยแหละ) และบทเรขาคณิตวิเคราะห์ จะทำให้เรียนเนื้อหาในบทแคลคูลัสได้ง่ายขึ้น ทำความเข้าใจได้เร็วขึ้นแน่นอน
แคลคูลัสที่น้อง ๆ ม.6 กำลังเรียนอยู่จะเป็นความรู้พื้นฐานที่จะนำไปใช้ต่อยอดในแคลคูลัสระดับมหาวิทยาลัย โดยแคลคูลัสระดับ ม.ปลาย จะเน้นฟังก์ชันพหุนาม แต่ในระดับมหาวิทยาลัยจะเพิ่มส่วนของฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันลอการิทึม ฟังก์ชันตรีโกณมิติเข้าไปด้วย และบางคณะอาจมีเนื้อหาในบทเรียน ม.ปลาย อื่น ๆ เพิ่มอีกด้วย เช่น เวกเตอร์ ลำดับและอนุกรม เป็นต้น
คำตอบของคำถามนี้ขึ้นอยู่กับแต่ละบุคคล แต่ละอาชีพว่าจำเป็นต้องนำความรู้แคลคูลัสไปใช้มากหรือน้อยแค่ไหน หรือบางอาชีพอาจไม่ได้ใช้ความรู้แคลคูลัสเลย
แต่สำหรับน้อง ๆ ม.6 แน่นอนว่าต้องเรียนบทแคลคูลัสเพื่อนำไปใช้ในการสอบในห้องเรียน และหลายคนต้องใช้สอบเข้าเพื่อศึกษาต่อในระดับมหาวิทยาลัย
และถ้าน้อง ๆ อยากประกอบอาชีพเกี่ยวกับนักพัฒนาโปรแกรมคอมพิวเตอร์ อาจารย์ นักวิจัยทางด้านวิทยาศาสตร์ และวิศวกร ความรู้เกี่ยวกับแคลคูลัสนี้จะสำคัญอย่างมากสำหรับน้อง ๆ เพราะแคลคูลัสเป็นพื้นฐานของสูตรทางคณิตศาสตร์และวิทยาศาสตร์ (โดยเฉพาะฟิสิกส์) หลายสูตรเลยน้าา
ดูคลิปติวฟรี แคลคูลัส ม.6
คลิปติว แคลคูลัส ม.6 จาก SmartMathPro
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
เป็นยังไงบ้างง สำหรับสรุปเนื้อหาเรื่องแคลคูลัส ม.6 ที่พี่เอามาฝาก สำหรับใครที่มีแพลนจะเรียนต่อในคณะสายวิทย์ อาจจะต้องเจอกับเรื่องแคลคูลัสอีกครั้งในระดับมหาลัยฯ ซึ่งพอเป็นระดับที่สูงขึ้น เนื้อหาก็จะยากขึ้นเป็นธรรมดา ดังนั้นพี่เลยอยากแนะนำให้ทบทวนบทนี้ให้ดี ๆ น้า โดยอาจจะทบทวนจากการทำโจทย์เยอะ ๆ ให้ตัวเองคุ้นกับโจทย์ที่หลากหลายแนว แต่ถ้าใครไม่รู้จะไปหาโจทย์จากไหนมาฝึกก็สามารถเข้าไปดาวน์โหลดข้อสอบแคลคูลัส ม.6 กันได้เลยย
ส่วนน้อง ๆ ที่ยังไม่เข้าใจบทนี้ เวลาทำโจทย์อาจจะสับสนได้ พี่แนะนำว่าควรเก็บเนื้อหาให้แม่น ๆ ก่อน โดยอาจจะเริ่มจากกลับไปทบทวนบทที่ควรรู้ก่อนเรียนแคลคูลัสก็ได้น้า
แต่ถ้าใครกังวลว่าถ้าทบทวนเองแล้วก็ยังไม่เข้าใจ อยากได้คนช่วยอธิบายเนื้อหาและทำโจทย์บทแคลคูลัส รวมถึงเนื้อหาคณิตศาสตร์ ม.ปลาย บทอื่น ๆ พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เพราะแพ็กม.5 – ม.6 เรียนได้ถึง 2 ปี และแพ็ก ม.4 – ม.6 เรียนได้ถึง 3 ปี พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมาก นอกจากนี้ยังพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ และถ้าแพ็กไม่ตรงกับบทที่โรงเรียนสอนก็สามารถเลือกเป็นคอร์สแยกบทได้เพราะมีคอร์สติวแยกบทของคณิต ม.ปลายทุกบทเลย แน่นอนว่ามีส่วนลดพิเศษเช่นกันน้า ใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
ลำดับและอนุกรม ม.6 สรุปเนื้อหาพร้อมตัวอย่างโจทย์และวิธีทำ
สถิติ ม.6 สรุปเนื้อหาสถิติและข้อมูล พร้อมโจทย์แบบจัดเต็ม ! - SmartMathPro
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
A-Level คณิต 1, A-Level คณิต 2 TCAS67 สอบอะไรบ้าง? อัปเดตล่าสุด
ข้อสอบ A-Level คณิต 1 และคณิต 2 67 ออกอะไรบ้าง ? พร้อมแจกบทน่าเก็บ
A Level คณิตศาสตร์ 1 กับ 2 ต่างกันยังไง? ยื่นคณะไหนได้บ้าง?
บทความ แนะนำ
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
