หลังจากเรียนจบเทอม 1 กันไปแล้ว มีใครรู้สึกกังวลกับคณิต ม.ปลายบ้าง ? แน่นอนว่ายิ่งเรียนปีสูงขึ้นเท่าไหร่ เนื้อหามันก็ต้องยากขึ้นเรื่อย ๆ ใช่มั้ยย อาจจะทำให้หลายคนกังวลและกลัวว่าจะไม่เข้าใจในบางบทเรียน แต่ความเครียดนั้นจะหายไป เพราะพี่ ๆ ได้เตรียมสรุปคณิตศาสตร์มาให้ทุกคนได้อ่านก่อนสอบแล้ววว
ซึ่งบทเรียนที่พี่ ๆ เตรียมมาในวันนี้ก็เป็นหนึ่งในบทเรียนของคณิต ม.4 เทอม 2 อย่างเรื่อง ความสัมพันธ์และฟังก์ชัน
ใครที่ไม่เข้าใจเรื่องนี้ หรืออยากจะเตรียมตัวล่วงหน้า ควรอ่านบทความนี้น้าเพราะนอกจากจะสรุปเนื้อหาแล้ว ยังมีคลิป
ติวฟรีพร้อมโจทย์ให้ฝึกทำอีกด้วย !!
“ความสัมพันธ์” เป็นคำที่เราใช้กันบ่อยมาก เช่น ความสัมพันธ์แบบเพื่อน แฟน Friend Zone หรือ แม้กระทั่งความสัมพันธ์ระหว่างสิ่งของกับสิ่งของก็ตาม อย่างไรก็ตาม นักคณิตศาสตร์อยากลองนิยามคำว่า “ความสัมพันธ์” ให้ชัดเจนว่ามันมีหน้าตาเป็นอย่างไร มา !!! เดี๋ยวเราลองไปดูกันเลยยยย
ผลคูณคาร์ทีเซียน
บทนิยาม
ผลคูณคาร์ทีเซียนของเซต A และเซต B คือเซตของคู่อันดับ \left ( a,b \right ) ทั้งหมด
โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B
สามารถเขียนผลคูณคาร์ทีเซียนของเซต A และเซต B แทนด้วย A\times B
เช่น กำหนดให้ A=\left \{ 1,2,3 \right \} และ B=\left \{ a,b \right \}
ดังนั้น A\times B=\left \{ (1,a),(2,a),(3,a),(1,b),(2,b),(3,b) \right \}
ความสัมพันธ์
บทนิยาม
r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A\times B
เช่น กำหนดให้ A=\left \{ 1,2,3 \right \} และ B=\left \{ 1,3 \right \}
ถ้า r_{1}=\left \{ (x,y)\in A\times B\mid x<y \right \} จะสามารถเขียนแจกแจงสมาชิกได้ดังนี้ r_{1}=\left \{ (1,3),(2,3) \right \}
หรือเราสามารถเรียกได้ว่า r_{1} เป็นความสัมพันธ์ “น้อยกว่า” จาก A ไป B นั่นเอง
กราฟของความสัมพันธ์
ในหัวข้อนี้เราจะสนใจเฉพาะความสัมพันธ์ของจำนวนเท่านั้นนะ โดยเราสามารถนำความสัมพันธ์มาแสดงเป็นภาพได้โดยนำคู่อันดับในความสัมพันธ์มาแสดงเป็นพิกัดของจุดแล้ววางลงไปบนระนาบ XY ก็จะได้ออกมาเป็นกราฟของ
ความสัมพันธ์ต่าง ๆ
กราฟของความสัมพันธ์ r มีอยู่ 3 ลักษณะ
- กราฟมีลักษณะเป็นจุด
เช่น \left ( x,y \right ) เป็นสมาชิกของ \mathbb{Z}\times \mathbb{Z} ดังรูป - กราฟมีลักษณะเป็นเส้น
เช่น \left ( x,y \right ) เป็นสมาชิกของ \mathbb{R}\times \mathbb{R} มีเงื่อนไขเป็นสมการ ดังรูป - กราฟมีลักษณะเป็นพื้นที่
เช่น \left ( x,y \right ) เป็นสมาชิกของ \mathbb{R}\times \mathbb{R} มีเงื่อนไขเป็นอสมการ
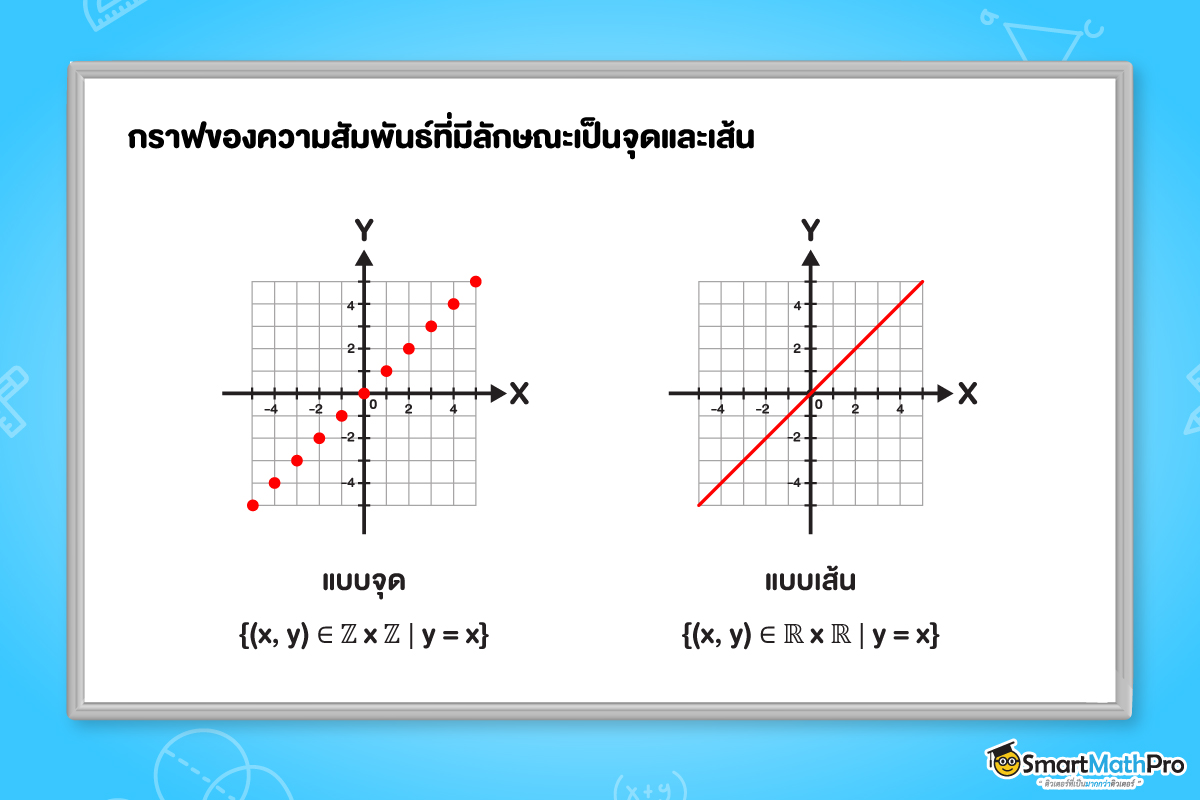
ข้อสังเกต
เรานำสมาชิกตัวหน้ามาเป็นค่าตำแหน่งบนแกน X และนำสมาชิกตัวหลังเป็นค่าตำแหน่งบนแกน Y แล้วใช้ค่าตำแหน่ง
ทั้งสองมาเป็นพิกัดในการลงจุดเพื่อวาดกราฟนั่นเอง
โดเมนและเรนจ์ของความสัมพันธ์
คราวนี้ก็มาถึงหัวข้อที่สำคัญมาก ๆ และน้อง ๆ ทุกคนจะได้เจอในข้อสอบอย่างแน่นอนนั่น คือ โดเมนและเรนจ์ของความสัมพันธ์ ซึ่งเราจะต้องหาทั้งในรูปแบบของเซตและกราฟได้ ดังนั้นเรามาทำความรู้จักกับบทนิยามของโดเมนและเรนจ์กันก่อนเลย
บทนิยาม
ให้ r เป็นความสัมพันธ์จาก A ไป B
- โดเมนของ r คือ เซตของสมาชิกตัวหน้าของคู่อันดับทั้งหมดใน r เขียนแทนด้วย D_r
- เรนจ์ของ r คือ เซตของสมาชิกตัวหลังของคู่อันดับทั้งหมดใน r เขียนแทนด้วย R_r
ตัวอย่างที่ 1 จงหาโดเมนและเรนจ์จากกราฟของความสัมพันธ์ที่กำหนดให้ต่อไปนี้
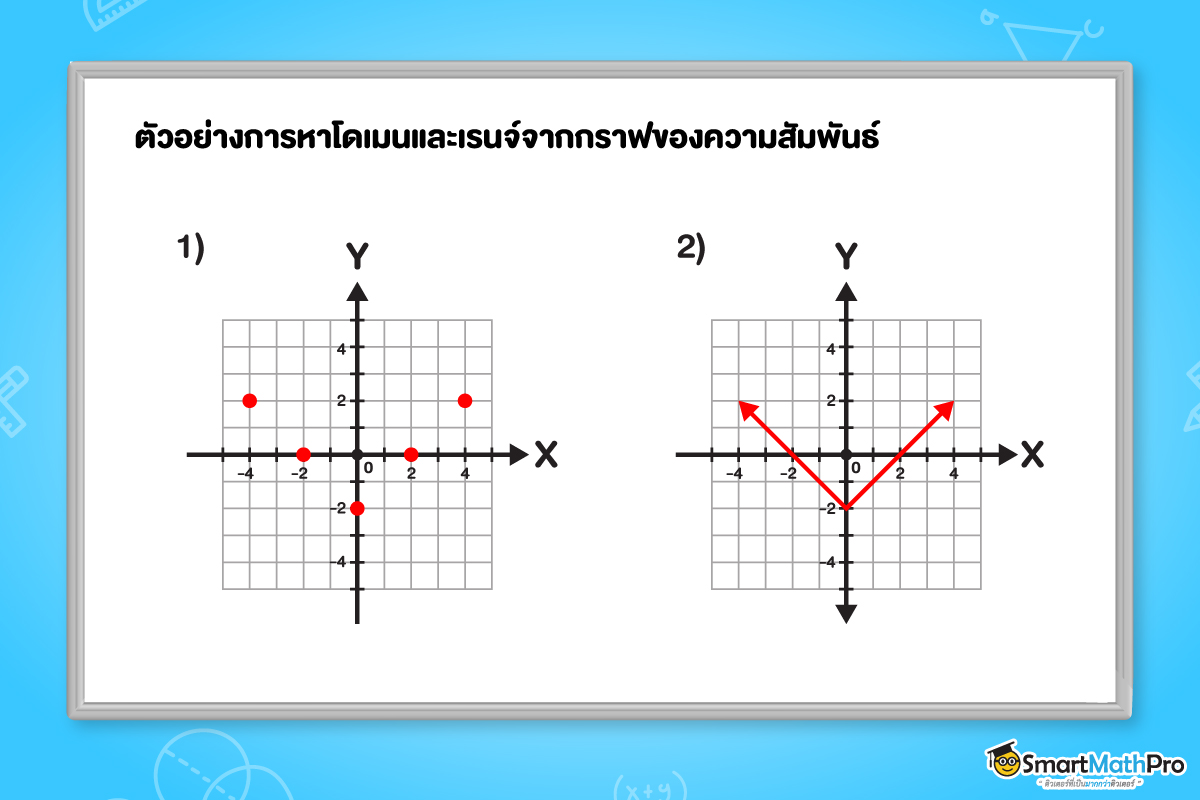
วิธีทำ
จากข้อ 1)
กำหนดให้เป็นกราฟของความสัมพันธ์ r_1
จะได้ว่า r_1=\left \{ \left ( -4, 2 \right ), \left ( -2, 0 \right ), \left ( 0, -2 \right ), \left ( 2, 0 \right ), \left ( 4, 2 \right )\right \}
ดังนั้น D_{r_1}=\left \{ -4, -2, 0, 2, 4 \right \} และ R_{r_1}=\left \{ -2, 0, 2 \right \}
จากข้อ 2)
แนวคิด เราสามารถมองเส้นจากกราฟของความสัมพันธ์ r_2 ได้ว่าเป็นจุดจำนวนมากเรียงต่อกัน จนกลายเป็นเส้น ดังนั้น วิธีการหาโดเมนและเรนจ์จากกราฟในข้อนี้ สามารถมองได้ด้วยวิธีคล้ายกับกับข้อ 1)
สมาชิกตัวหน้าของคู่อันดับจะเป็นจำนวนจริงทั้งหมดเลย (ตั้งแต่ -\infty จนถึง \infty )
ถ้าเริ่มมองจากแกน Y ด้านล่างขึ้นมา จะเห็นว่าสมาชิกตัวหลังของคู่อันดับจะเป็นจำนวนตั้งแต่ -2 จนถึง \infty
จะได้ว่า D_{r_2}=\mathbb{R} และ R_{r_2}=[-2, \infty )
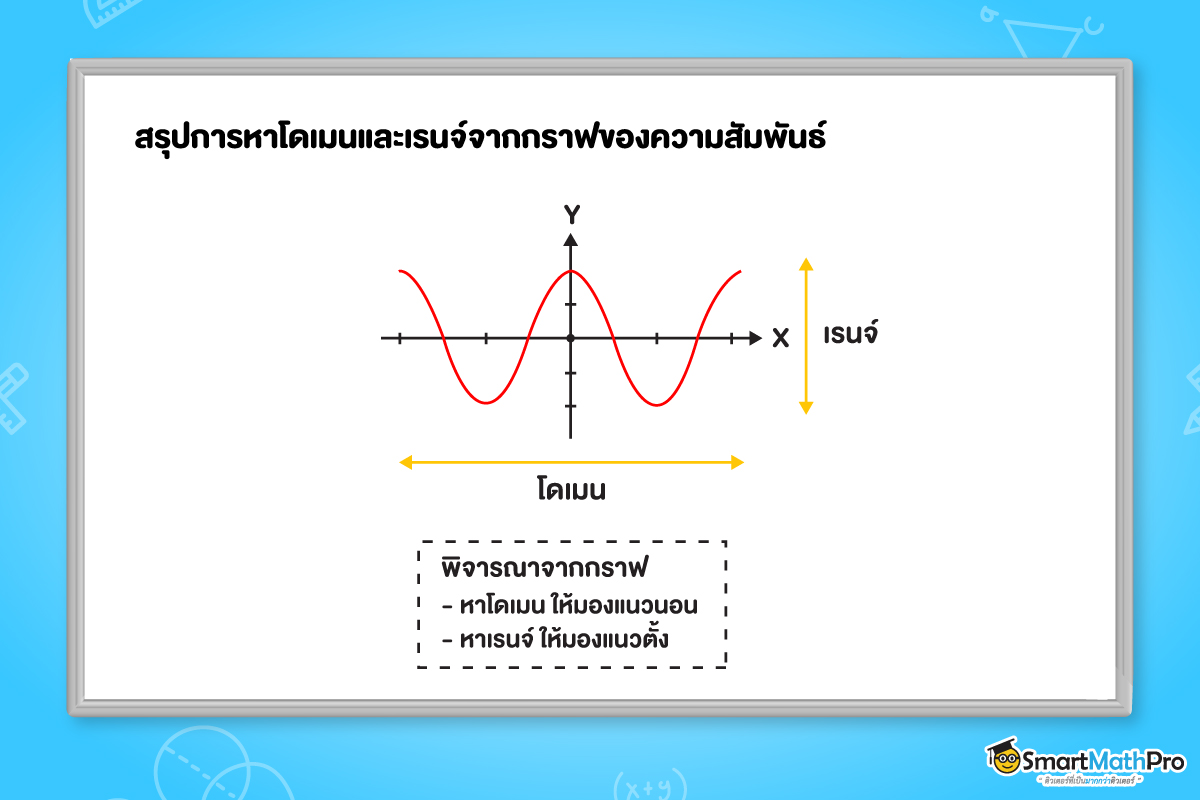
จากตัวอย่างก่อนหน้า เราสามารถสรุปการหาโดเมนและเรนจ์จากกราฟของความสัมพันธ์ได้เป็นดังนี้เลยย
นอกจากการหาโดเมนและเรนจ์จากกราฟของความสัมพันธ์แล้ว ถ้าโจทย์ให้ความสัมพันธ์ที่เขียนในรูปของเซตแบบบอกเงื่อนไข เราจะใช้เทคนิคในการพิจารณาเงื่อนไขแล้วหาโดเมนและเรนจ์ของความสัมพันธ์ ซึ่งจะมีขั้นตอนดังต่อไปนี้
เทคนิค การหาโดเมนและเรนจ์ด้วยวิธีพิจารณาจากเงื่อนไข
ให้พิจารณาเงื่อนไขดังนี้
- \frac{\blacktriangle }{\blacksquare }
จะได้ว่า \blacksquare \neq 0 (ตัวส่วนไม่เท่ากับศูนย์) - \sqrt[n]{\blacksquare }=\blacktriangle (เมื่อ n เป็นจำนวนคู่)
จะได้ว่า \blacksquare \geqslant 0 และ \blacktriangle \geqslant 0
ตัวอย่างที่ 2 จงหาโดเมนและเรนจ์ของความสัมพันธ์ต่อไปนี้
1) r_1=\left \{ \left ( x, y \right )\mid y=\frac{1}{x+1} \right \}
วิธีทำ
พิจารณา \frac{1}{x+1} จะเห็นว่า x+1 ต้องไม่เป็นศูนย์
นั่นคือ x\neq -1
ดังนั้น D_{r_1}=\left \{x \mid x\neq -1 \right \}=\mathbb{R}-\left \{ -1 \right \}
พิจารณา y=\frac{1}{x+1}
จะได้ว่า y\neq 0
ดังนั้น R_{r_1}=\left \{y \mid y\neq 0 \right \}=\mathbb{R}-\left \{ 0 \right \}
2) r_2=\left \{ \left ( x, y \right )\mid y=\sqrt{x} \right \}
วิธีทำ
พิจารณา \sqrt{x}
จะได้ว่า x ต้องไม่เป็นจำนวนลบ
ดังนั้น D_{r_2}=\left \{x \mid x\geqslant 0 \right \}=[0, \infty )
เนื่องจาก x ไม่เป็นจำนวนลบ แล้วแทน x ด้วย 0 ใน \sqrt{x} จะได้ค่าที่น้อยที่สุดเท่ากับ 0
ดังนั้น R_{r_2}=\left \{y \mid y\geqslant 0 \right \}=[0, \infty )
ตัวผกผันของความสัมพันธ์
บทนิยาม
ตัวผกผันของความสัมพันธ์ r คือความสัมพันธ์ที่เกิดจากการสลับที่ของสมาชิกตัวหน้า และสมาชิกตัวหลัง
ในแต่ละคู่อันดับที่เป็นสมาชิกของ r
ตัวผกผันของความสัมพันธ์ r เขียนแทนด้วย r^{-1}
เช่น ถ้า r=\left \{ \left ( 1,2 \right ), \left (3, 4 \right ),\left ( 5, 6 \right ) \right \} แล้วจะได้ว่า r^{-1}=\left \{ \left ( 2, 1 \right ),\left ( 4, 3 \right ),\left ( 6,5 \right ) \right \}
ก่อนหน้านี้เราเคยเขียนความสัมพันธ์ให้อยู่ในรูปเซตแบบบอกเงื่อนไข ดังนั้นเราก็สามารถเขียนตัวผกผันของความสัมพันธ์ให้อยู่ในรูปของเซตแบบบอกเงื่อนไขได้เช่นกัน
เช่น
แบบที่ 1: r^{-1}=\left \{ \left (y, x \right )\in B\times A\mid \left ( x, y \right )\in r \right \} หรือ
แบบที่ 2: r^{-1}=\left \{ \left (x, y \right )\in A\times B\mid \left ( y, x \right )\in r \right \}
ซึ่งถ้าน้อง ๆ ลองสังเกตจะเห็นว่าการเขียนทั้งสองแบบเกิดจากการสลับ x และ y แต่แบบที่ 1 จะสลับที่ด้านหน้าเพียง
อย่างเดียว ส่วนแบบที่ 2 จะสลับที่เพียงด้านหลังอย่างเดียวเท่านั้น ถ้าใครเผลอไปเขียนตัวผกผันของความสัมพันธ์แล้วสลับทั้งสองที่จะผิดได้นะ !
ฟังก์ชัน
หลังจากที่เรารู้จักความสัมพันธ์กันไปแล้ว มันก็จะมีความสัมพันธ์บางอย่างที่เราได้ให้ชื่อมันเอาไว้ ซึ่งความสัมพันธ์ประเภทนี้จะเป็นพื้นฐานสำคัญที่นำไปต่อยอดในหัวข้ออื่น ๆ ได้อีกมากมาย ความสัมพันธ์นี้มีชื่อว่า “ฟังก์ชัน”
ความหมายของฟังก์ชัน
บทนิยาม
ฟังก์ชัน คือ ความสัมพันธ์ที่คู่อันดับสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น ถ้ามีสมาชิกตัวหน้าเหมือนกันแล้ว สมาชิกตัวหลังต้องเหมือนกัน
จากบทนิยามข้างต้น พี่จะขออธิบายง่าย ๆ แบบนี้น้าา ฟังก์ชัน คือ ความสัมพันธ์ที่สมาชิกตัวหน้าแต่ละตัวจะจับกับสมาชิกตัวหลังเพียงค่าเดียวเท่านั้น !!
ฟังก์ชันโดยส่วนใหญ่มักจะเขียนแสดงได้ 3 รูปแบบคือ แผนภาพ เซต และกราฟของฟังก์ชัน โดยกราฟของฟังก์ชันจะถูก
ใช้บ่อยและมีความสำคัญมากกก พี่เลยจะขอยกให้เป็นหัวข้อใหญ่หลังจากพี่อธิบายการเขียนฟังก์ชันสองแบบแรกน้าา
1. เขียนในรูปของแผนภาพ
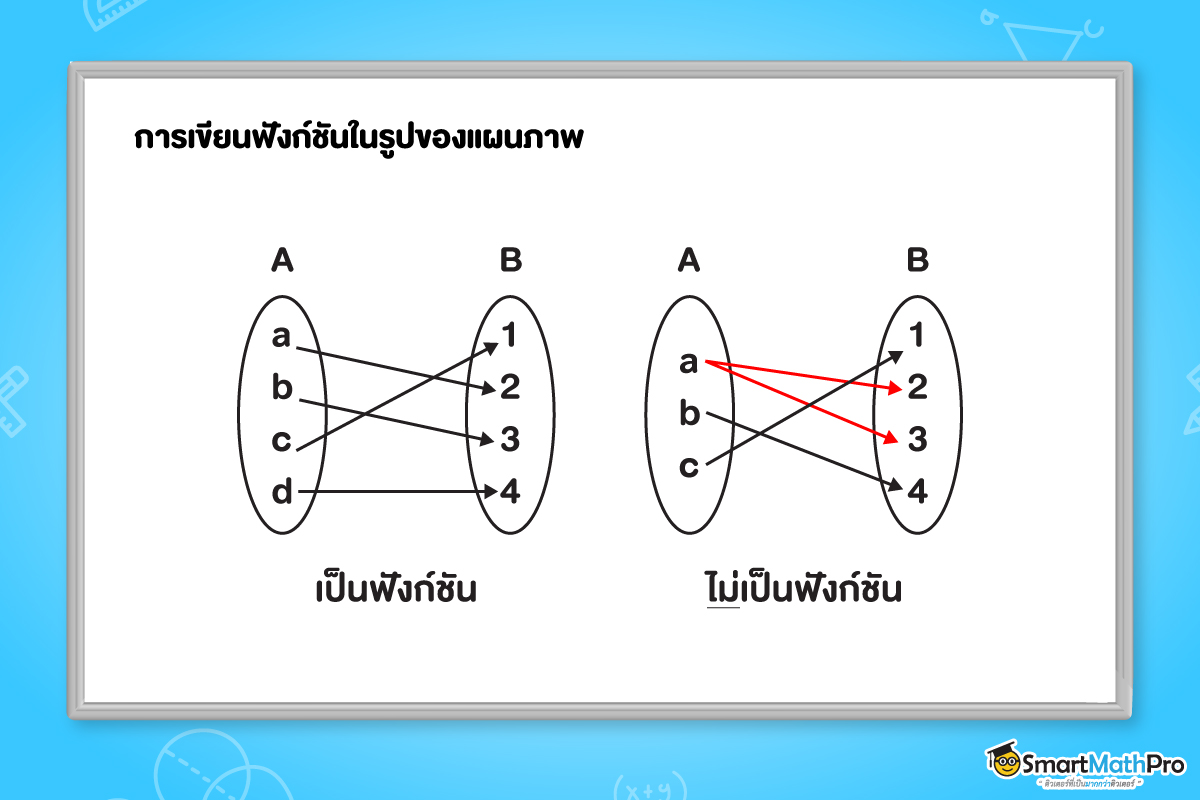
2. เขียนในรูปของเซต
สามารถเขียนได้ 2 แบบ คือ แบบแจกแจงสมาชิกตรง ๆ และ แบบบอกเงื่อนไข เช่น
แบบแจกแจงสมาชิก
- f=\left \{ \left ( 1,a \right ),\left ( 2,b \right ),\left ( 3,c \right )\right \}
แบบบอกเงื่อนไข
- g=\left \{ \left (x,y \right )|y = 2x+1 \right \}
ตัวอย่างที่ 3 กำหนดให้ A = \left \{ -1,0,1 \right \} จงพิจารณาความสัมพันธ์ต่อไปนี้ว่าเป็นฟังก์ชันหรือไม่
1. f=\left \{ \left (x,y \right )\in A\times A|y = x \right \}
วิธีทำ
จาก f เมื่อเขียนความสัมพันธ์แบบแจกแจงสมาชิกจะได้
f=\left \{ \left (-1,-1 \right ) \left (0,0 \right )\left (1,1 \right )\right \}
สังเกตว่า สมาชิกของแต่ละตัวใน f ไม่มีคู่อันดับตัวไหนเลยที่ “ถ้าเลขตัวหน้าในคู่อันดับซ้ำกันแล้วตัวหลังไม่ซ้ำกัน”
ดังนั้น f เป็นฟังก์ชัน
2. g=\left \{ \left (x,y \right)\in A\times A|y^{2} = x \right \}
วิธีทำ
จาก g เมื่อเขียนความสัมพันธ์แบบแจกแจงสมาชิกจะได้
g=\left \{ \left (0,0 \right ) \left (1,1 \right )\left (1,-1 \right )\right \}
สังเกตว่า g มีคู่อันดับ \left (1,1 \right ) และ \left (1,-1 \right ) มีเลขตัวหน้าในคู่อันดับซ้ำกันคือ เลข 1 และมีตัวหลังต่างกันคือ 1 และ -1
ดังนั้น g ไม่เป็นฟังก์ชัน
กราฟของฟังก์ชัน
ตัวอย่างที่ 4 จงพิจารณาว่ากราฟต่อไปนี้เป็นฟังก์ชันหรือไม่
1.
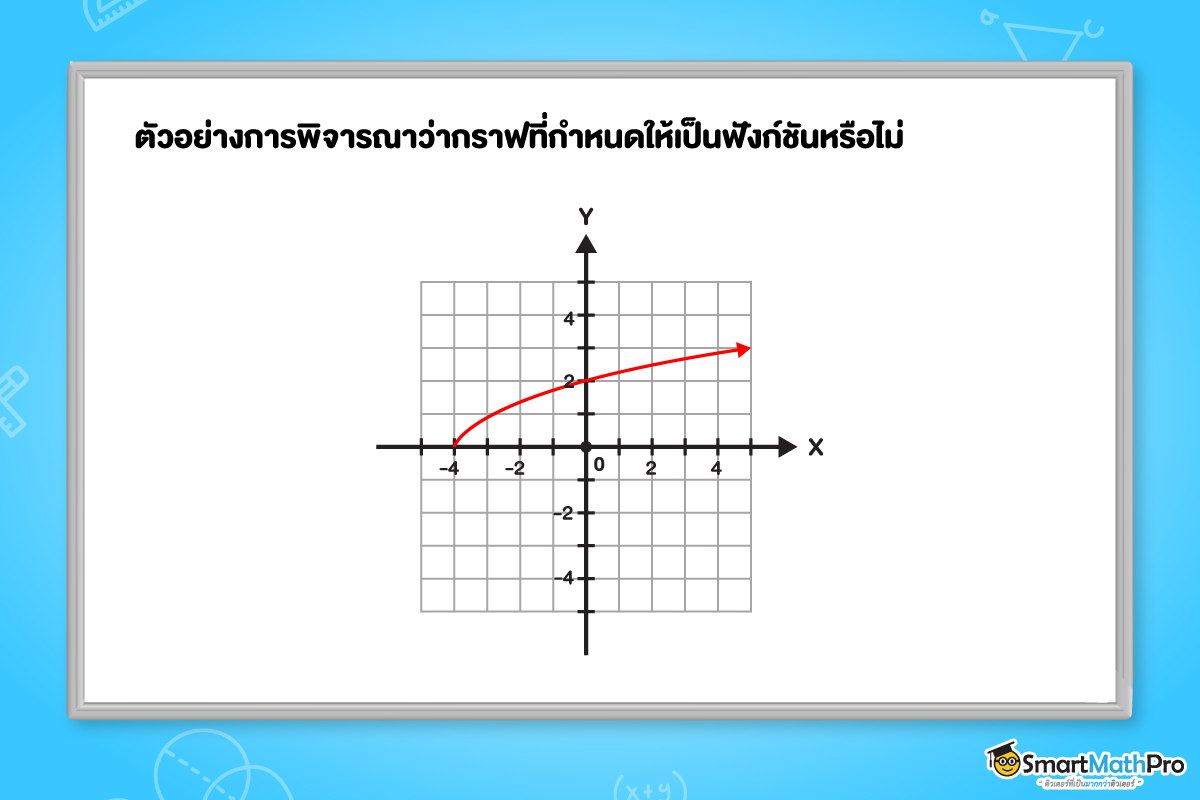
วิธีทำ
ลากเส้นตรงในแนวตั้ง (ขนานแกน Y) ให้ตัดผ่านกราฟ สังเกตว่า ไม่มีกรณีใดเลยที่เส้นตรงลากผ่านกราฟแล้วเกิดจุดตัดกราฟมากกว่า 1 จุด ดังนั้น กราฟดังกล่าวเป็นฟังก์ชัน
2.
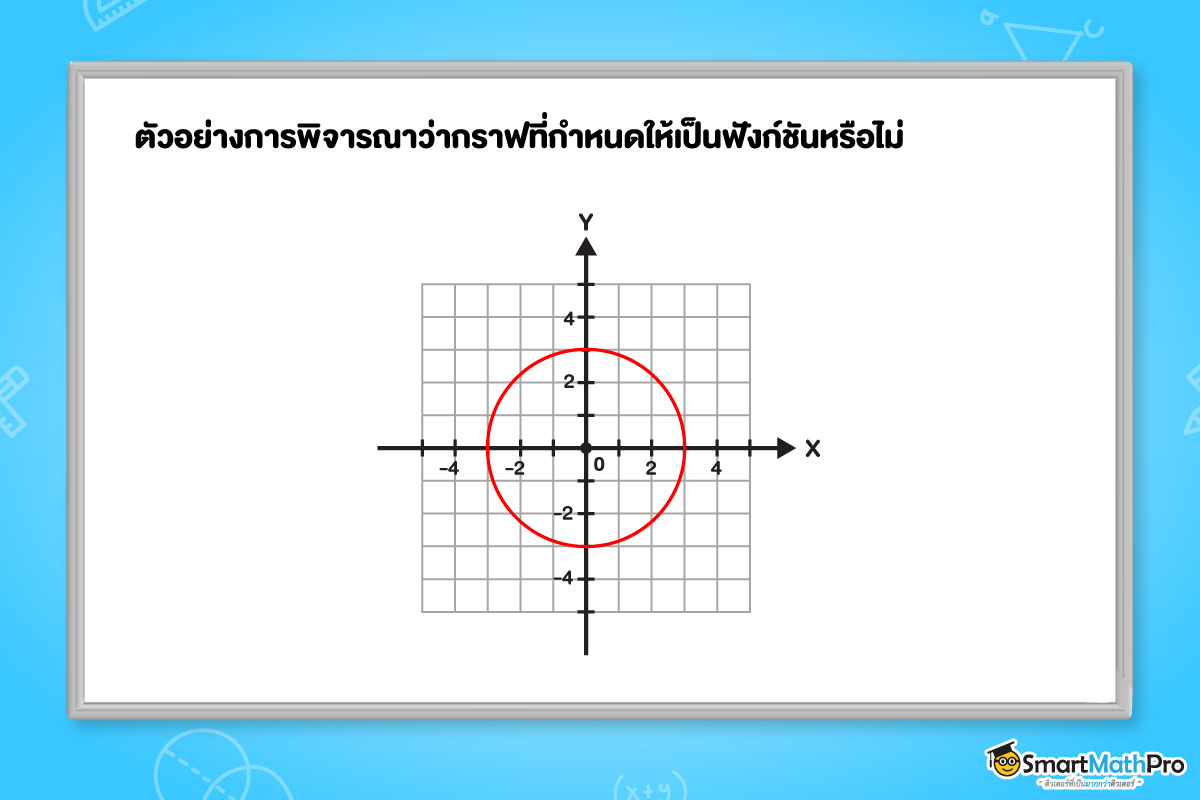
วิธีทำ
ลากเส้นตรงในแนวตั้ง (ขนานแกน Y) ให้ตัดผ่านกราฟ สังเกตว่า มีบางกรณีที่เส้นตรงลากผ่านกราฟแล้วเกิดจุดตัดกราฟมากกว่า 1 จุด เช่น
ดังนั้น กราฟดังกล่าวไม่เป็นฟังก์ชัน
ประเภทของฟังก์ชัน
ฟังก์ชันที่เราศึกษานั้นสามารถแบ่งออกได้เป็น 3 ประเภทหลัก ๆ ได้แก่
1. ฟังก์ชันจาก A ไป B
บทนิยาม
f เป็นฟังก์ชันจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็น A และเรนจ์เป็นสับเซตของ B
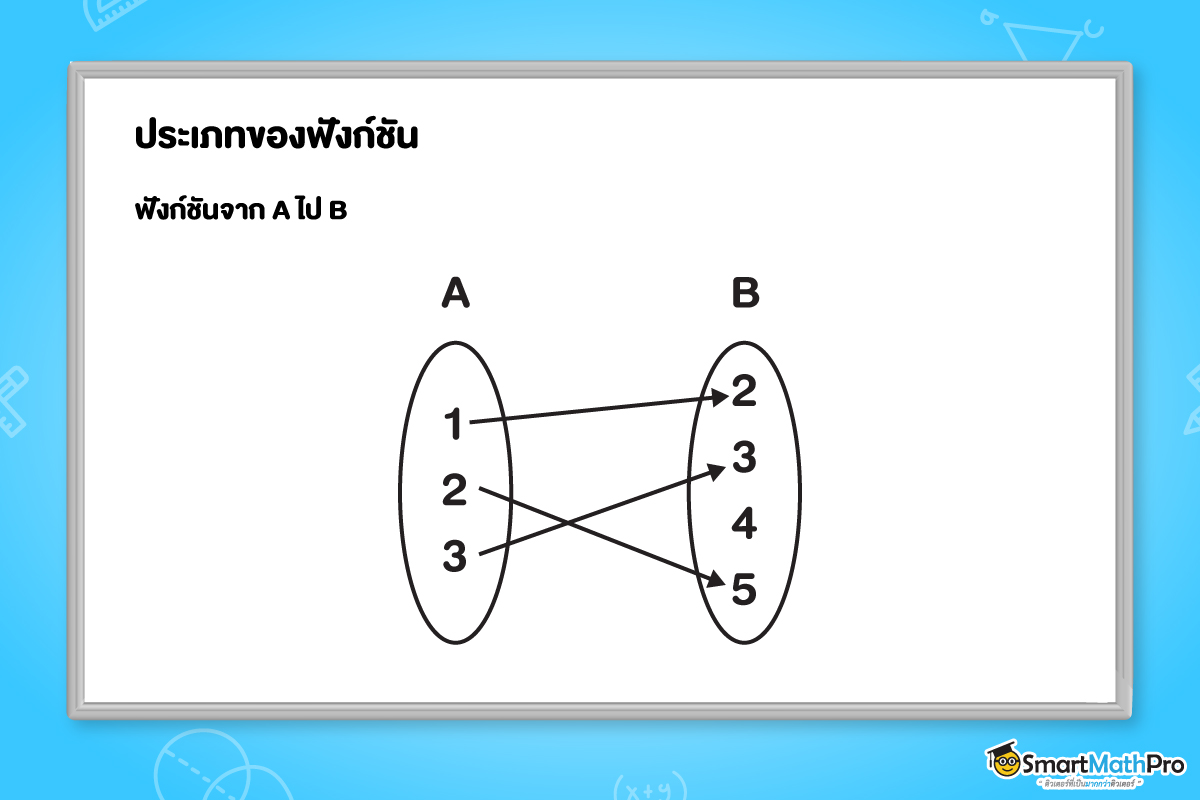
สังเกตได้ว่าฟังก์ชัน จาก A ไป B จะมีสมาชิกตัวหน้าอยู่ใน A และมีสมาชิกตัวหลังอยู่ใน B เสมอ โดยสมาชิกใน A จะถูกใช้ในฟังก์ชันหมดทุกตัว แต่สมาชิกใน B จะถูกใช้ในฟังก์ชันหมดทุกตัวหรือไม่ก็ได้
2. ฟังก์ชันจาก A ไปทั่วถึง B
บทนิยาม
f เป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็น A และเรนจ์เป็น B
เช่น
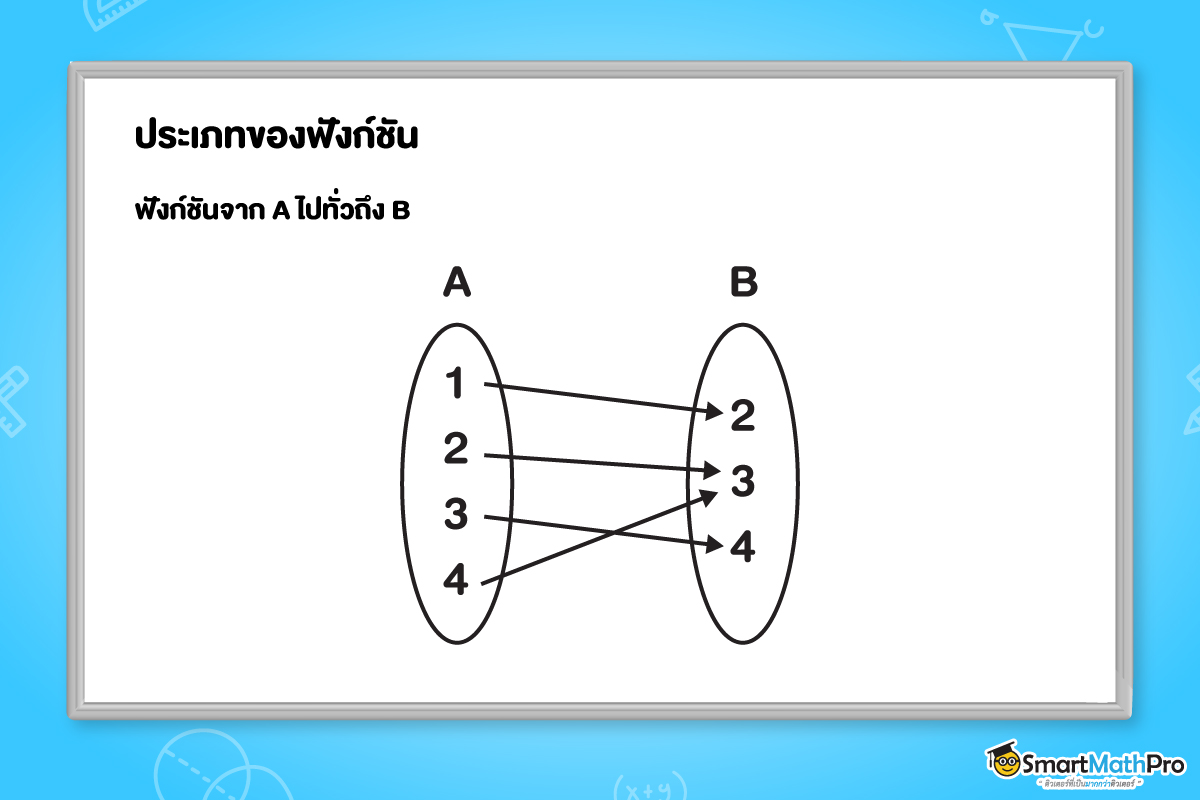
สังเกตได้ว่าฟังก์ชัน จาก A ไปทั่วถึง B สมาชิกทุกตัวใน B จะถูกใช้ในฟังก์ชันทั้งหมด
3. ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B
บทนิยาม
f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันจาก A ไป B ซึ่งสำหรับ x_{1} และ x_{2} ใด ๆ ใน A ถ้า f\left ( x_{1} \right )=f\left ( x_{2} \right ) แล้ว x_{1}= x_{2}
เช่น
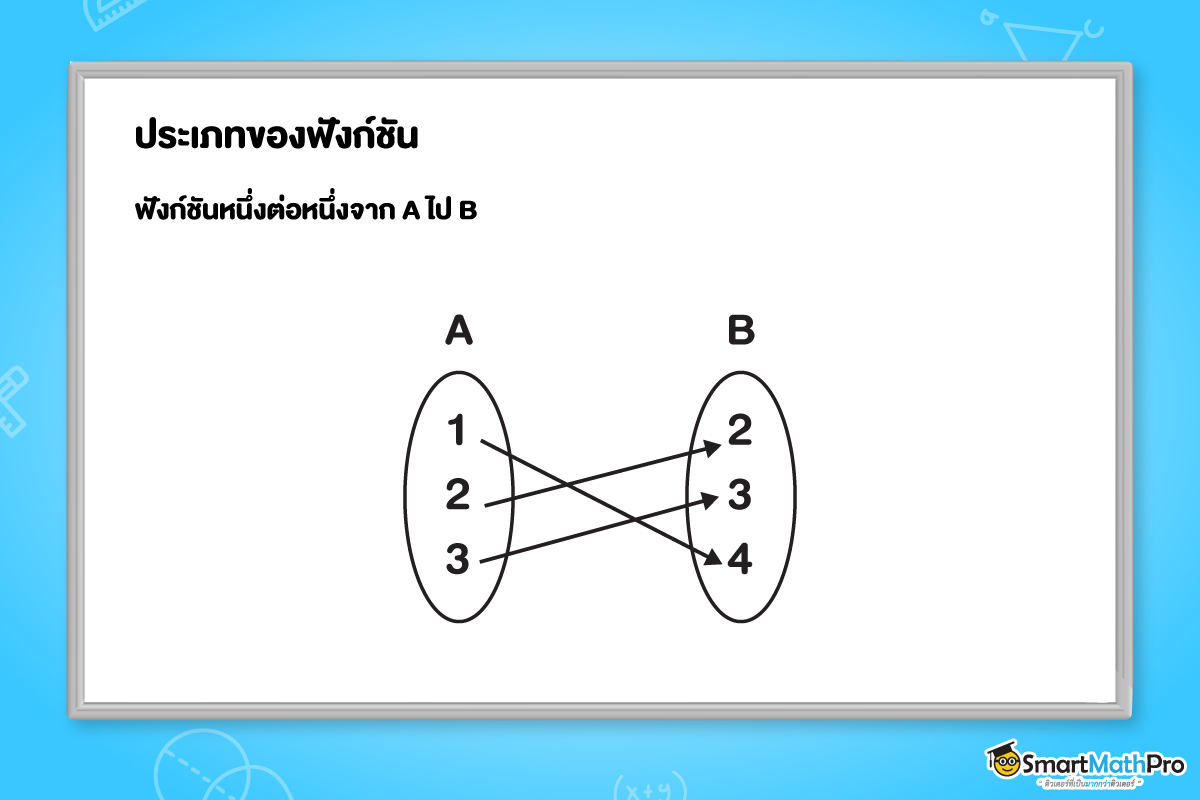
สังเกตได้ว่าฟังก์ชัน 1-1 จาก A ไป B สมาชิกใน B จะถูกใช้ในฟังก์ชันไม่เกิน 1 ตัวเสมอ
ซึ่งการตรวจสอบกราฟว่าเป็นฟังก์ชัน 1-1 มั้ย สามารถทำได้โดยลากเส้นในแนวนอน (ขนานแกน X) ให้ตัดกับกราฟ
ถ้ามีกรณีใดเกิดจุดตัดระหว่างกราฟและเส้นในแนวนอนมากกว่า 1 จุด กราฟดังกล่าวจะไม่เป็นฟังก์ชัน 1-1
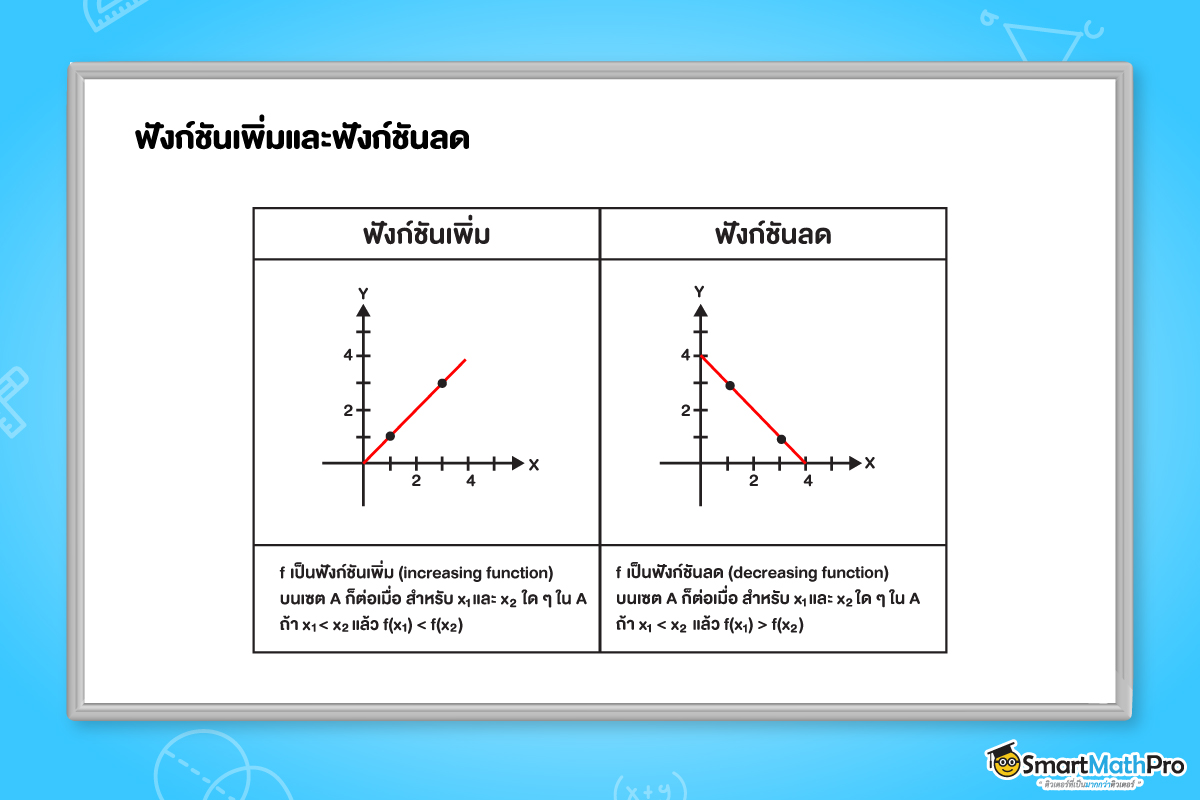
ฟังก์ชันเพิ่มและฟังก์ชันลด
บทนิยาม
ให้ f เป็นฟังก์ชันซึ่งมีโดเมนและเรนจ์เป็นสับเซตของจำนวนจริง และ A เป็นสับเซตของโดเมน
เช่น ให้ f เป็นฟังก์ชันที่มีกราฟดังรูป
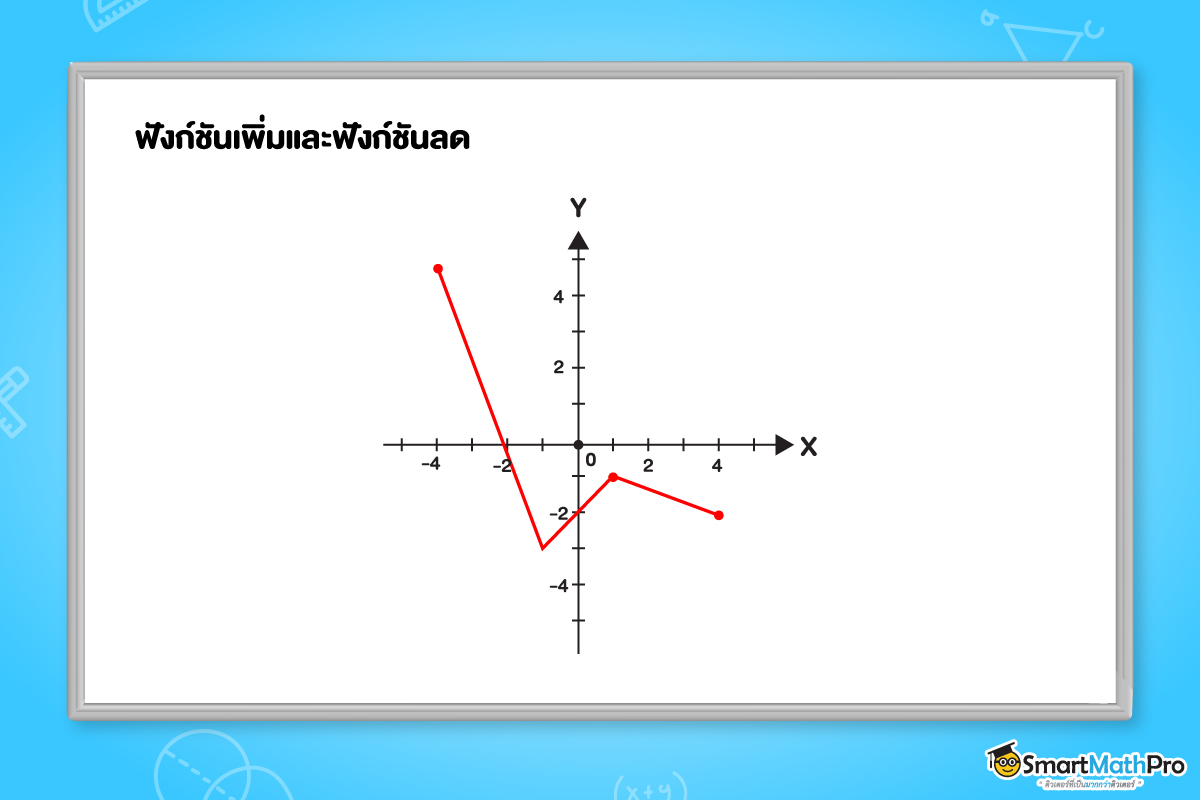
f เป็นฟังก์ชันเพิ่มบนช่วง [-1,1] และ
f เป็นฟังก์ชันลดบนช่วง [-4,-1] และ [1,4]
การดำเนินการของฟังก์ชัน
เรารู้จักฟังก์ชันกันมาพอสมควรแล้ว เดี๋ยวเราลองมาสร้างฟังก์ชันใหม่ที่ใช้ฟังก์ชันเดิมเป็นองค์ประกอบดีกว่า เนื่องจาก ฟังก์ชันที่มีโดเมนและเรนจ์เป็นเซตของจำนวนที่สามารถบวก ลบ คูณ และหารได้ ดังนั้นเราจะใช้การดำเนินการต่าง ๆ
มาสร้างฟังก์ชันใหม่ดูบ้าง
พีชคณิตของฟังก์ชัน
บทนิยาม
ให้ f และ g เป็นฟังก์ชันที่มีโดเมนและเรนจ์เป็นสับเซตของ \mathbb{R}
กำหนดฟังก์ชัน f+g,f-g,fg และ \frac{f}{g} ดังนี้
(f+g)(x)=f(x)+g(x)
(f-g)(x)=f(x)-g(x)
(fg)(x)=f(x)\cdot g(x)
(\tfrac{f}{g})(x)=\frac{f(x)}{g(x)} เมื่อ g(x)\neq 0
ตัวอย่างที่ 5 ให้ f(x)=2x+1 และ g(x)=x-3 จงหา f-g และ fg
วิธีทำ เนื่องจากโดเมนของ f คือ \mathbb{R} และโดเมนของ g คือ \mathbb{R} ดังนั้น
(f-g)(x)=f(x)-g(x)=(2x+1)-(x-3)
=2x+1-x+3=x+4
และ
(fg)(x)=f(x)\cdot g(x)=(2x+1)\cdot(x-3)
=2x^{2}-6x+x-3=2x^{2}-5x-3
ฟังก์ชันประกอบ
บทนิยาม
ให้ f และ g เป็นฟังก์ชัน โดยที่ R_{f}\cap D_{g}\neq \varnothing
ฟังก์ชันประกอบของ f และ g เขียนแทนด้วย g \circ f คือฟังก์ชันที่โดเมน คือ
D_{g \circ f }= \left \{ x\in D_{f}|f(x)\in D_{g}\right \}
และกำหนด g \circ f โดย
g \circ f (x)=g(f(x)) สำหรับทุก x ใน D_{g \circ f }
ตัวอย่างที่ 6 ให้ f(x)=x-1 และ g(x)=3x จงหา g \circ f (x) และ
f \circ g (x)
วิธีทำ จาก f(x)=x-1 และ g(x)=3x จะได้
g \circ f (x)=g(f(x))
=g(x-1)
=3(x-1)=3x-3
และ
f \circ g (x)=f(g(x))
=f(3x)
=(3x)-1=3x-1
ฟังก์ชันผกผัน
ในเรื่องตัวผกผันของความสัมพันธ์ เราหาได้จากการสลับสมาชิกตัวหน้าและสมาชิกตัวหลังของแต่ละคู่อันดับที่เป็นสมาชิกในความสัมพันธ์นั้น ลองคิดดูดี ๆ ฟังก์ชันก็เป็นความสัมพันธ์หนึ่งเช่นกัน ดังนั้น เราจึงสามารถใช้วิธีเดียวกันในการหาได้ แต่ตัวผกผันของฟังก์ชันนั้นไม่จำเป็นต้องเป็นฟังก์ชันเสมอไป
เช่น f=\left \{ (3,4),(6,4) \right \} เป็นฟังก์ชัน
แต่เราจะได้ f^{-1}=\left \{ (4,3),(4,6) \right \} ไม่เป็นฟังก์ชัน
บทนิยาม
ให้ f เป็นฟังก์ชัน จะได้ว่า f มีฟังก์ชันผกผัน ก็ต่อเมื่อ f เป็นฟังก์ชัน 1 – 1
ตัวอย่างที่ 7 ฟังก์ชัน f เป็นฟังก์ชัน 1 – 1 ซึ่งกำหนดโดย f(x)=2x-1 จงหาฟังก์ชันผกผัน
วิธีทำ
ให้ f(x)=y
จะได้ y=2x-1 ต้องการหาตัวผกผัน
(เปลี่ยน x เป็น y และ เปลี่ยน y เป็น x)
จะได้ x=2y-1
(จัดรูปโดยเขียน y ให้อยู่ในรูปของ x)
จะได้ y=\frac{x+1}{2}
ดังนั้น f^{-1}(x)=\frac{x+1}{2}
ดูคลิปติวฟรี ความสัมพันธ์และฟังก์ชัน ม.4
ดูคลิปติวฟรีอื่น ๆ ได้ที่ YouTube : SmartMathPro
เป็นยังไงบ้างกับสรุปบทความสัมพันธ์และฟังก์ชัน ม.4 อาจจะเนื้อหาเยอะหน่อย แต่ถ้าน้อง ๆ ทบทวนเนื้อหา รวมถึง
ฝึกทำโจทย์บ่อย ๆ พี่เชื่อว่่าทุกคนจะเก่งขึ้น และทำคะแนนสอบได้ดีแน่นอนน ซึ่งถ้าใครอยากได้โจทย์ไปฝึกซ้อมมือเพิ่มเติม เสริมความมั่นใจ พี่ก็มีโจทย์และแบบฝึกหัดในคลังข้อสอบให้ทุกคนได้ไปดาวน์โหลดมาฝึกทำกันแบบฟรี ๆ ด้วยน้าา
แวะเข้าไปดูกันได้เลยย
แต่ถ้าน้อง ๆ คนไหนที่ทบทวนเนื้อหา รวมถึงฝึกทำโจทย์เองแล้วก็ยังไม่เข้าใจ มาลงเรียนคอร์สความสัมพันธ์และฟังก์ชัน
ก็ได้น้าา เพราะในคอร์ส พี่ปั้นจะสอนเนื้อหาแบบปูพื้นฐาน พาตะลุยโจทย์ ข้อสอบและแบบฝึกหัดกว่า 150 ข้อ !!
อยากแนะนำให้น้องทบทวนบทนี้เยอะ ๆ เพราะถ้าพื้นฐานของเรื่องนี้แน่น น้อง ๆ ก็จะเรียนบทอื่นต่อได้สบายย
ดูรายละเอียดเพิ่มเติม คลิกเล้ยย
บทความ แนะนำ
จำนวนจริง ม.4 สรุปครบม้วนเดียวจบ พร้อมแจกโจทย์จำนวนจริงและวิธีทำ
เซต (Set) คืออะไร สรุปเนื้อหาเซต ม.4 พร้อมโจทย์และเฉลย
ตรรกศาสตร์ ม.4 สรุปครบทุกเนื้อหาพร้อมโจทย์ตรรกศาสตร์และวิธีทำ - SmartMathPro
คณิตศาสตร์ ม.4 เทอม 1,2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
คณิตศาสตร์ ม.5 เทอม 1 เทอม 2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
บทความ แนะนำ
คณิตศาสตร์ ม.4 เทอม 1, ม.4 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
