น้อง ๆ หลายคนคงจะเคยเสียคะแนนวิชาคณิตศาสตร์ไปในจุดที่เนื้อหาคล้ายกันสุด ๆ เช่น การกลับเครื่องหมาย “ลบเป็นบวก” หรือ “บวกเป็นลบ” ที่ทำให้น้อง ๆ เสียคะแนนข้อนั้นไปได้แบบฟรี ๆ เลย ซึ่งนี่ก็เป็นแค่ส่วนหนึ่งของจุดคล้ายกันในเนื้อหาคณิตศาสตร์ ม.ปลาย เท่านั้น
วันนี้พี่เลยมาสรุป 8 จุดคล้ายกันและจุดที่ควรระวังในเนื้อหา คณิตศาสตร์ ม.ปลาย มาให้น้อง ๆ ได้รู้และทบทวนกันให้แม่นยิ่งขึ้น เพื่อไม่ให้พลาดกันในห้องสอบจริง โดยจะมีเรื่องอะไรบ้าง ตามไปดูกันได้เลยยยย
ลำดับการเขียนสมาชิก VS คู่อันดับ
{1,2} กับ (1,2) ถึงจะเขียนคล้ายกัน แต่ คุณสมบัติของมันนั้นต่างกันอย่างสิ้นเชิง ซึ่งน้อง ๆ หลายคนอาจจะสงสัยว่า สมาชิกภายในเซต สามารถสลับที่หรือสลับตำแหน่งกันได้ไหม คำตอบคือ สลับได้น้า โดยจะได้เซตที่เท่ากัน เช่น {1,2} และ {2,1} นั้นถือว่าเป็นเซตที่เท่ากัน
แต่ถ้าหากเป็นในกรณีของ คู่อันดับ เช่น (1,2) กับ (2,1) จะถือว่าเป็นคู่อันดับที่ไม่เท่ากัน เพราะคู่อันดับนั้น ตัวหน้า จะมีชื่อเฉพาะ คือ คู่อันดับตัวหน้า ส่วนตัวหลังก็จะมีชื่อว่า คู่อันดับตัวหลัง นั่นเอง
เซตว่าง VS เซตของเซตว่าง
หลายคนอาจเข้าใจผิดคิดว่า {\varnothing} นั่นคือเซตว่าง ซึ่งในความเป็นจริงแล้ว เซตว่างนั้นเขียนสัญลักษณ์แทนด้วย \varnothing ไม่มีวงเล็บปีกกา โดยเซตว่าง คือ เซตที่ไม่มีสมาชิกเลย หรือมีจำนวนสมาชิกเท่ากับ 0
แต่บางคนอาจจะสับสนกับ เซต {\varnothing} ที่ไม่ใช่เซตว่างแต่เป็น “เซตของเซตว่าง” โดยมีสมาชิกข้างในเป็น \varnothing เพียงตัวเดียว นั่นก็คือมีจำนวนสมาชิกของ {\varnothing} เท่ากับ 1 นั่นเอง
สรุปอีกครั้งน้า เซตว่าง สามารถเป็นสมาชิกในเซตได้ในกรณีที่มีวงเล็บปีกกา { } ครอบอยู่ แต่ถ้าเซตว่าง เป็นสัญลักษณ์โดด ๆ ไม่มีปีกกาครอบอยู่เลยจะถือว่าเป็น เซตที่ไม่มีสมาชิก นั่นเอง
เป็นสมาชิกของ VS เป็นสับเซตของ
สัญลักษณ์ “\in” กับ “\subset” เขียนคล้ายกัน แต่ในบทเซตใช้ต่างกัน ระวังอย่าใช้ผิดความหมาย !!
หลายคนน่าจะรู้จักกับสัญลักษณ์ กับ 2 สัญลักษณ์นี้ที่สามารถแสดงความสัมพันธ์ในเซตใด ๆ ได้ นั่นก็คือ “\in” หรือ “เป็นสมาชิกของ” ซึ่งมีไว้แสดงว่า สิ่งใดเป็นสมาชิกในเซตนั้น ๆ บ้าง เช่น 1 \in {1,2} จะเห็นว่า 1 เป็นสมาชิกของเซต หรืออยู่ในเซต {1,2} นั่นเอง
และ “\subset” หรือ “เป็นสับเซตของ” มีไว้แสดงว่า เซตใดเป็น สับเซต หรือ เซตย่อย ของเซตนั้น ๆ เช่น {1} \subset {1,2} ซึ่งจะเห็นว่า {1} เป็นเซตย่อยของ {1,2} เพราะภายใน {1} มีสมาชิกเป็น 1 ซึ่งมาจากส่วนหนึ่งของ 1,2 นั่นเอง
ข้อสังเกตว่า หากพิจารณาความเป็น สมาชิก ของเซตใด ๆ เราจะดูว่าตัวนั้น ๆ อยู่ในเซตที่เราสนใจหรือเปล่า แต่ถ้าหากพิจารณาความเป็น สับเซต จะต้องพิจารณาสมาชิกของเซตย่อย แล้วดูว่า สมาชิกทุกตัวในเซตย่อยนั้น เป็นสมาชิกของอีกเซตไหม
จุดคล้ายกันใน บทตรรกศาสตร์ ม.4 เทอม 1
การสลับที่ประพจน์ย่อย และ, หรือ, ก็ต่อเมื่อ VS ถ้า … แล้ว …
ตัวเชื่อมประพจน์ “และ” “หรือ” “ก็ต่อเมื่อ” สามารถสลับประพจน์ที่เชื่อมกันอยู่ได้ เลยอาจทำให้บางคนคิดว่า ตัวเชื่อมประพจน์ “ถ้า…แล้ว…” ก็น่าจะสลับที่ได้ด้วย ซึ่งบอกเลยว่าไม่จริงน้า
น้อง ๆ คงจะเคยเห็นตารางค่าความจริงมาบ้างแล้ว สำหรับกรณีการเชื่อมประพจน์ต่าง ๆ (และ, หรือ, ถ้า…แล้ว…, ก็ต่อเมื่อ) เราลองมาทบทวนตารางค่าความจริงอีกรอบกันดีกว่า
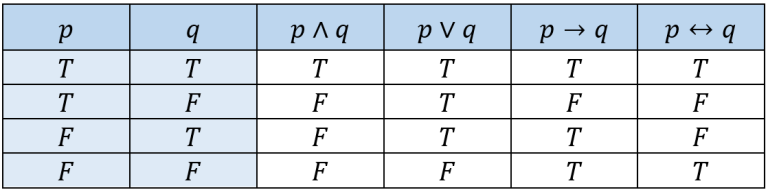
ถ้าเราพิจารณากรณีของ p เป็นจริง (T) และ q เป็นเท็จ (F) และสลับเป็นกรณีของ q เป็นจริง (T) และ p เป็นเท็จ (F) นั้น จะเห็นว่า ค่าความจริงในกรณีของการเชื่อมประพจน์ p กับ q ด้วย “และ” “หรือ” และ “ก็ต่อเมื่อ” ก็จะยังคงได้ค่าความจริงที่ตรงกัน ในขณะที่การเชื่อมประพจน์ p กับ q ด้วย “ถ้า…แล้ว…” จะได้ค่าความจริงที่ไม่ตรงกัน นั่นหมายความว่า p\rightarrow q ไม่สมมูลกับ q\rightarrow p
จุดคล้ายกันใน บทฟังก์ชันตรีโกณมิติ ม.5 เทอม 1
sin tan VS cos
สมบัติบางอย่าง ฟังก์ชัน \textrm{sin} และ \textrm{tan} มีเหมือนกัน แต่ไม่ได้หมายความว่าฟังก์ชัน \textrm{cos} จะมีเหมือนกันน้า เป็นอีกจุดที่ควรระวังเลย
น้อง ๆ คงคุ้นเคยกับการหาค่าฟังก์ชันตรีโกณต่าง ๆ สำหรับมุมที่มีค่าติดลบนั้น ในกรณีของ \textrm{sin} กับ \textrm{tan} จะต้องดึงเครื่องหมายลบออกมาด้านหน้าฟังก์ชันตรีโกณมิตินั้น ๆ เช่น \textrm{sin(-A) = -sin A} แต่ถ้าหากเป็นกรณีของ \textrm{cos} เราไม่ต้องดึงเครื่องหมายลบออกมา หรือก็คือ \textrm{cos(-A) = cos A}
ทั้งนี้ เราสามารถอธิบายได้ด้วยวงกลมหนึ่งหน่วย โดยการเริ่มต้นวัดมุมนั้น เราจะเริ่มที่จุดขวาสุดของวงกลมหนึ่งหน่วย หรือก็คือพิกัด (1,0) แล้วลากมุมทวนเข็มนาฬิกา ในกรณีมุมมีค่าเป็นบวก หรือลากมุมตามเข็มนาฬิกา ในกรณีมุมมีค่าเป็นลบ จะเห็นว่า การคิดค่าฟังก์ชันตรีโกณมิติของมุมติดลบนั้น เราจะต้องคิดในรูปแบบการวัดมุมตามเข็มนาฬิกา หรือวิ่งไปหาจตุภาค (Quadrant) ที่ 4 ซึ่งบนจตุภาคที่ 4 นั้น ค่า \textrm{sin} และ \textrm{tan} มีค่าเป็นลบพอดี และค่า \textrm{cos} มีค่าเป็นบวกพอดี
ดังนั้น เราสามารถคิดมุมกรณีที่มีค่าเป็นลบเหมือนกับคิดมุมบนจตุภาคที่ 4 เพื่อนำเครื่องหมายลบออกไปจากมุม โดยเครื่องหมายลบจะติดอยู่ข้างหน้าแทนในกรณีที่เป็น \textrm{sin} กับ \textrm{tan} แต่จะไม่มีเครื่องหมายลบติดอยู่ข้างหน้า กรณีที่เป็น \textrm{cos}
เอกลักษณ์ตรีโกณมิติ VS สูตรมุมสองเท่า
สมบัติบางอย่าง แค่เปลี่ยนเครื่องหมายไป ก็ทำให้ได้ผลลัพธ์ที่ต่างกัน ดังนั้นระวังเครื่องหมายผิดชีวิตเปลี่ยน !!
น้อง ๆ คงจะรู้จักกับเอกลักษณ์ของตรีโกณมิติ ซึ่งสามารถพิสูจน์ได้จาก “วงกลมหนึ่งหน่วย” โดยจุด (x, y) ใด ๆ ของวงกลมหนึ่งหน่วย จะมีความสัมพันธ์ดังสมการ x^{2} + y^{2} = 1 นอกจากนี้ สำหรับฟังก์ชันไซน์และฟังก์ชันโคไซน์ สามารถนิยามด้วยค่า y และ x ตามลำดับ
ซึ่งเมื่อนำค่าของ \textrm{sinA} และ \textrm{cosA} (เมื่อ \textrm{A} เป็นมุมหรือจำนวนจริงใด ๆ) เข้าไปแทนในความสัมพันธ์ของวงกลมหนึ่งหน่วย จะได้เป็น cos^{2}A+sin^{2}A=1 (หรือสลับที่การบวกเป็น sin^{2}A+cos^{2}A=1 ในรูปที่เราคุ้นตากัน)
แต่เอกลักษณ์ตรีโกณมิตินี้ดันไปคล้ายกับ สูตร ๆ หนึ่ง ของฟังก์ชันตรีโกณมิตินี่น่ะสิ ซึ่งก็คือ cos^{2}A-sin^{2}A ซึ่งสูตรนี้เป็นของ มุมสองเท่าของโคไซน์ และจะมีค่าเท่ากับ \textrm{cos2A} นั่นเอง
จุดคล้ายกันใน บทเวกเตอร์ ม.5 เทอม 1
ผลคูณเชิงสเกลาร์ VS ผลคูณเชิงเวกเตอร์
การคูณกันในบทเวกเตอร์มีด้วยกัน 2 แบบ นั่นคือ ผลคูณเชิงสเกลาร์ และ ผลคูณเชิงเวกเตอร์ แต่การคูณทั้ง 2 อย่างนี้มีคุณสมบัติที่ต่างกันอย่างสิ้นเชิง
สำหรับ ผลคูณเชิงสเกลาร์ และ ผลคูณเชิงเวกเตอร์ นั้น เป็นการดำเนินการที่สำคัญและข้อสอบชอบนำมาออกในบทเวกเตอร์อยู่บ่อย ๆ สำหรับ ผลคูณเชิงสเกลาร์ (Dot product) ผลลัพธ์ที่ได้จะเป็นจำนวนจริง ซึ่งไม่ว่าเราจะนำเวกเตอร์ไหนมาดำเนินการก่อนหรือหลังก็ตาม ผลลัพธ์ที่ได้ก็จะยังคงเป็นจำนวนจริงที่เท่ากัน
ทั้งนี้ สำหรับ ผลคูณเชิงเวกเตอร์ (Cross product) ผลลัพธ์ที่ได้จะเป็นเวกเตอร์ซึ่งมีทิศทาง ยิ่งไปกว่านั้น การสลับลำดับการดำเนินการของผลคูณเชิงเวกเตอร์ มีผลต่อทิศทาง ซึ่งจะทำให้ได้เวกเตอร์ที่ไม่เท่ากัน กล่าวคือ หากมี \vec{u} กับ \vec{v}
– นำ \vec{u} ขึ้นก่อน แล้ว cross ด้วย \vec{v}
– เทียบกับการนำ \vec{v} ขึ้นก่อน แล้ว cross ด้วย \vec{u}
ผลลัพธ์ที่ได้จะเป็นเวกเตอร์ที่มีทิศทางตรงข้ามกัน
จุดคล้ายกันใน บทลำดับและอนุกรม ม.6 เทอม 1
สูตรการหาพจน์ทั่วไปของลำดับเรขาคณิต VS สูตรการหาผลบวก n พจน์แรก ของอนุกรมเรขาคณิต
สูตรของลำดับเรขาคณิตและอนุกรมเรขาคณิตนั้นมีค่าคงที่ ที่ใช้ในสูตรเหมือนกัน แต่ตัวสูตรจะไม่เหมือนกัน น้อง ๆ ต้องใช้ให้ถูกและเหมาะสมกับสิ่งที่ต้องการหาน้า
สิ่งที่สำคัญของลำดับเรขาคณิต คือ การหาพจน์ทั่วไป หรือพจน์ที่ n ของลำดับเรขาคณิต โดยที่มาของสูตร เราจะคิดเทียบจากพจน์ที่ 1 หรือ a_1 แล้วดูว่าจะต้องคูณด้วยอัตราส่วนร่วมหรือ r ของลำดับเรขาคณิต ทั้งหมดกี่ครั้ง จึงจะไปถึงพจน์ที่ n หรือ a_n
ซึ่งจะเห็นว่า ต้องคูณด้วยอัตราส่วนร่วมของลำดับเรขาคณิตจำนวนทั้งหมด n-1 ครั้ง ถึงจะได้สูตรของพจน์ทั่วไป a_n=a_1r^{n-1}
แต่ระวัง (กาดอกจันพันครั้ง !!!) ถ้าเป็นอนุกรมเรขาคณิต สูตรผลรวม n พจน์แรกของอนุกรมเรขาคณิต ไม่ได้ยกกำลังด้วย n-1 น้า แต่ยกกำลังด้วย n เท่านั้น
อ่านมาจนถึงตรงนี้ น้อง ๆ คงเห็นแล้วว่ามีหลายบทของคณิตศาสตร์ ม.ปลายที่เนื้อหาบางจุดคล้ายกันมาก แถมน้อง ๆ ก็มีโอกาสเจอข้อสอบหลอกเรื่องเหล่านี้ด้วย ดังนั้นถ้าใครไม่อยากพลาดคะแนนไป พี่แนะนำให้ฝึกทำแบบฝึกหัดของเรื่อง
นั้น ๆ ให้แม่นที่สุด เพราะจะช่วยให้น้อง ๆ เข้าใจเนื้อหาบทต่าง ๆ และจุดที่ข้อสอบมักจะหลอกมากขึ้น
ทั้งนี้สำหรับคนที่ฝึกทำโจทย์เองแล้ว แต่ก็ยังมีจุดที่ผิดหรือไม่เข้าใจอยู่ อยากได้ตัวช่วยในการเรียนคณิตศาสตร์ ม.ปลาย ให้เข้าใจเนื้อหาแบบเจาะลึกพี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เพราะแพ็กม.5 – ม.6 เรียนได้ถึง 2 ปี และแพ็ก ม.4 – ม.6 เรียนได้ถึง 3 ปี พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมาก นอกจากนี้ยังพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ และถ้าแพ็กไม่ตรงกับบทที่โรงเรียนสอนก็สามารถเลือกเป็นคอร์สแยกบทได้เพราะมีคอร์สติวแยกบทของคณิต ม.ปลายทุกบทเลย แน่นอนว่ามีส่วนลดพิเศษเช่นกันน้า ใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
คณิตศาสตร์ ม.4 เทอม 1 และเทอม 2 เรียนอะไรบ้าง ? สรุปครบทั้งคณิตพื้นฐานและเพิ่มเติม
เซต (Set) คืออะไร สรุปเนื้อหาเซต ม.4 พร้อมโจทย์และเฉลย
ตรรกศาสตร์ ม.4 สรุปเนื้อหาครบ พร้อมโจทย์ตรรกศาสตร์และวิธีทำ
คณิตศาสตร์ ม.5 เทอม 1 และเทอม 2 เรียนอะไรบ้าง ? สรุปครบทั้งคณิตพื้นฐานและเพิ่มเติม
ตรีโกณมิติ ม.5 สรุปพร้อมแจกโจทย์และสูตรจัดเต็ม !!
เวกเตอร์ ม.5 สรุปทุกเนื้อหา พร้อมโจทย์และวิธีทำที่ทุกคนห้ามพลาด!
คณิตศาสตร์ ม.6 เทอม 1 และเทอม 2 เรียนอะไรบ้าง ? สรุปครบทั้งคณิตพื้นฐานและเพิ่มเติม
ลำดับและอนุกรม ม.6 สรุปเนื้อหาพร้อมตัวอย่างโจทย์และวิธีทำ
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
