
ถ้าพูดถึง “เวกเตอร์” น้อง ๆ บางคนอาจจะคุ้นชื่อนี้จากวิชาฟิสิกส์ แต่ทุกคนรู้ไหมว่า เราจะได้เจอเวกเตอร์ในเนื้อหาวิชาคณิตศาสตร์ ม.ปลาย ด้วยน้าาา ซึ่งเวกเตอร์ในวิชาคณิตศาสตร์จะมีทฤษฎีบท สูตร และเนื้อหาอะไรที่เราต้องรู้บ้าง วันนี้พี่มาช่วยตอบทุกคำถามที่น้อง ๆ อยากรู้และอาจจะสงสัยให้แล้วในบทความนี้ แถมยังมีตัวอย่่างโจทย์ให้ทุกคนได้ฝึกทำพร้อมเฉลยละเอียดให้ด้วย ถ้าทุกคนพร้อมแล้ว ไปอ่านกันเลยยย
สนใจหัวข้อไหน ... กดอ่านเลย
Toggleเวกเตอร์

เวกเตอร์และสมบัติของเวกเตอร์
น้อง ๆ บางคนอาจคุ้นเคยกับปริมาณที่บ่งบอกขนาดต่าง ๆ เช่น ความยาว ระยะทาง ปริมาตร มวล อุณหภูมิ เป็นต้น เพื่อบอกความมากหรือน้อยของสิ่งนั้น ดังตัวอย่างประโยคเหล่านี้ในชีวิตประจำวันของน้อง ๆ
น้อง ๆ อาจเคยถามแม่ค้าว่า…
“แม่ค้าคะ มีไม้บรรทัดยาว 100 เซนติเมตรขายไหมคะ”
อาจเคยได้ยินเพื่อนบ่นว่า…
“วันนี้อากาศร้อนมากเลย ในแอปพลิเคชันบอกว่าอุณหภูมิ 32 องศา แต่ Feels Like 35 องศาแน่ะ !!”
หรืออาจได้ยินแม่พูดว่า…
“แมวของแม่กินเก่งมาก แม่ต้องซื้ออาหารแมวถุงใหญ่สุดที่มีน้ำหนัก 20 กิโลกรัมทุกเดือนเลย”
การบอกปริมาณบางอย่างสามารถบอกเพียงขนาดอย่างเดียวได้ ดังประโยคข้างต้น แต่ปริมาณบางอย่างไม่สามารถทำได้ จะต้องบอกขนาดควบคู่กับการพิจารณาทิศทางด้วย อ่านเพียงเท่านี้อาจฟังดูประหลาดสำหรับน้อง ๆ บางคนที่ไม่คุ้นเคย แต่พี่จะลองยกตัวอย่างต่อไปนี้
น้อง ๆ อาจเคยได้ยินคนถามซินแสว่า…
“ซินแสคะ จากบ้านหนูเดินทางไปทางทิศเหนือประมาณ 500 เมตรก็จะถึงแม่น้ำ ทำเลบ้านหนูดีไหมคะ”
หรือเคยได้ยินคนพากย์เรือยาวว่า…
“เรือยาวลำนี้เคลื่อนที่ไปข้างหน้าด้วยความเร่ง 4 เมตรต่อวินาทียกกำลังสองเลยทีเดียวครับบบ”
น้อง ๆ ที่เคยเรียนวิทยาศาสตร์มาแล้วบางคนอาจจะคุ้นเคยกับคำว่า “เวกเตอร์” มาบ้าง พี่จะขอสรุปความหมายของปริมาณทั้งสองแบบพร้อมทั้งชื่อเรียกไว้ดังนี้
ชนิดของปริมาณ
- ปริมาณสเกลาร์ คือ มีขนาดเพียงอย่างเดียว เช่น มูลค่าของเงิน ระยะทาง ช่วงเวลา
- ปริมาณเวกเตอร์ คือ มีทั้งขนาดและทิศทาง เช่น แรงผลัก ระยะกระจัด ความเร็ว
ปริมาณสเกลาร์สามารถเขียนแทนด้วยจำนวนจริงได้เลย แต่ปริมาณเวกเตอร์จะต้องมีส่วนของเส้นตรงและหัวลูกศรมา
ระบุทิศทางด้วย โดยความยาวของส่วนของเส้นตรงจะเป็นตัวบอกขนาดนั่นเอง โดยสัญลักษณ์ที่น้อง ๆ จะได้เจอใน
เวกเตอร์ มีดังนี้

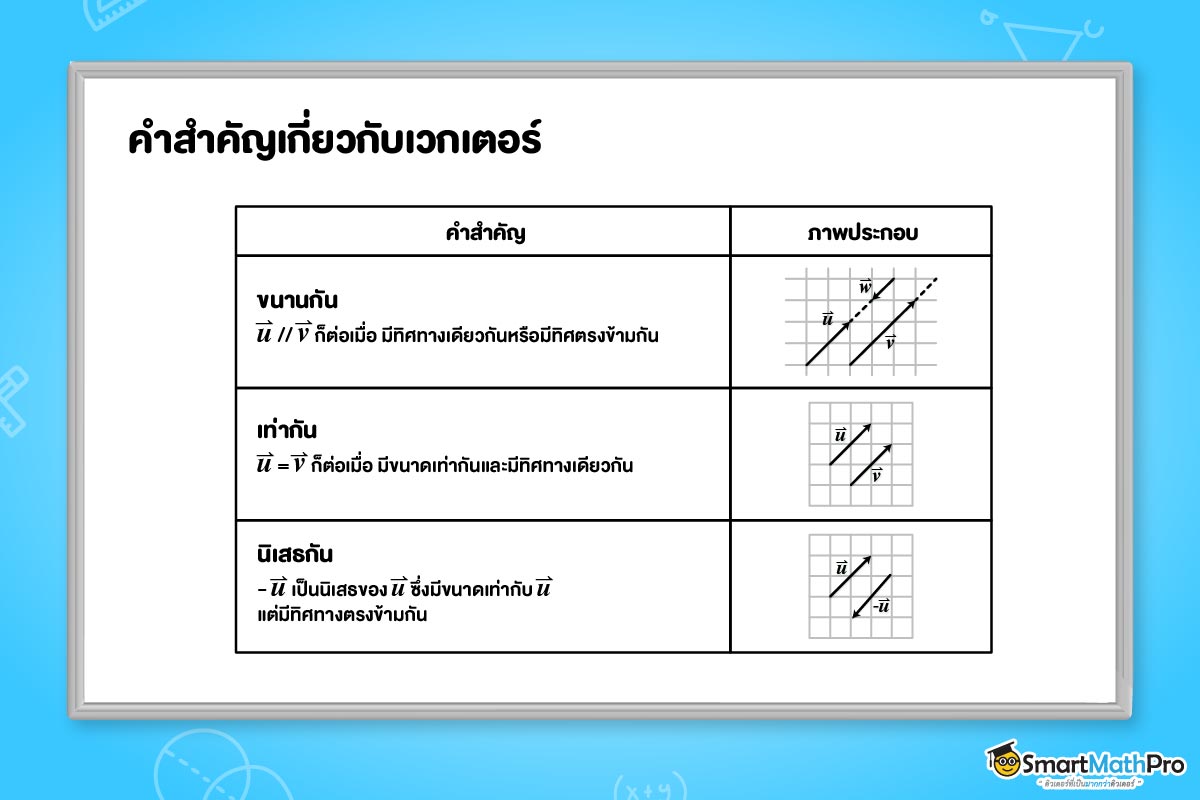
หลังจากที่เราทำความรู้จักสัญลักษณ์ซึ่งจะต้องเจอในบทนี้ พี่จะขออธิบายคำสำคัญ อย่างเช่น การขนานกันของเวกเตอร์ การเท่ากันของเวกเตอร์ และนิเสธของเวกเตอร์ให้น้อง ๆ เข้าใจอย่างง่าย ๆ ดังรูปด้านล่างนี้เลย
การบวกเวกเตอร์
การบวกเวกเตอร์มีความแตกต่างกับการบวกของจำนวนทางคณิตศาสตร์ทั่วไป เพราะการบวกเวกเตอร์เราต้องคำนึงถึงทั้งขนาดและทิศทางของเวกเตอร์ด้วย
บทนิยาม
ให้ \vec{u} และ \vec{v} เป็นเวกเตอร์ใด ๆ เขียน \vec{v} โดยให้จุดเริ่มต้นของ \vec{v} อยู่ที่จุดสิ้นสุดของ \vec{u} ผลบวกของ \vec{u} และ \vec{v} คือ เวกเตอร์ที่มีจุดเริ่มต้นอยู่ที่จุดเริ่มต้นของ \vec{u} และจุดสิ้นสุดอยู่ที่จุดสิ้นสุดของ \vec{v}
นั่นคือ การบวกของ \vec{u} และ \vec{v} คือการนำหัวของ \vec{v} ต่อที่หางของ \vec{u} แล้วผลบวกของ \vec{u} และ \vec{v} จะมีหางอยู่ที่หางของ \vec{u} และหัวอยู่ที่หัวของ \vec{v} หรือเราสามารถเรียกว่าการบวกเวกเตอร์แบบหางต่อหัวนั่นเอง
ผลบวกของ \vec{u} และ \vec{v} เขียนแทนด้วย \vec{u}+ \vec{v}
ตัวอย่างที่ 1
จงหาเวกเตอร์ \vec{u} + \vec{v}
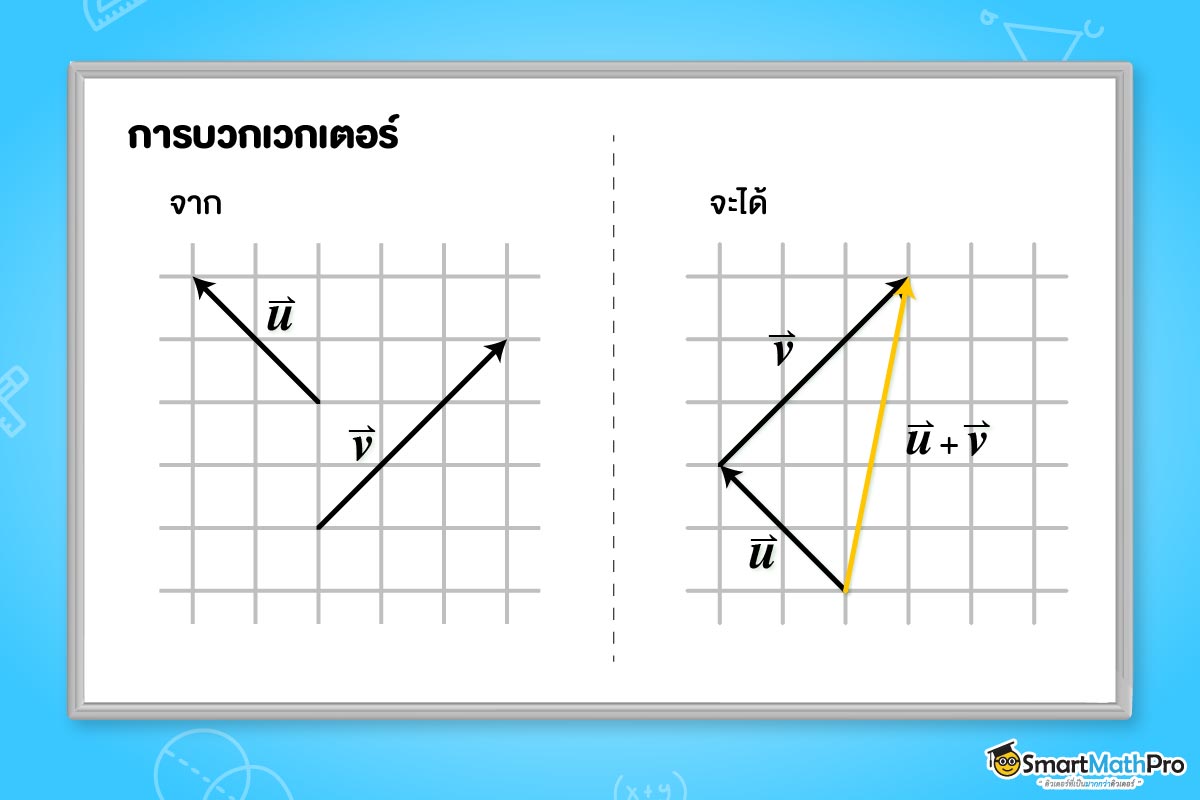
จากตัวอย่าง นำเวกเตอร์ \vec{v} มาต่อกับเวกเตอร์ \vec{u} ให้หางของเวกเตอร์ \vec{v} ต่อที่หัวของเวกเตอร์ \vec{u} แล้วเวกเตอร์ลัพธ์ \vec{u}+ \vec{v} จะลากจากหางของเวกเตอร์ \vec{u} ไปที่หัวของเวกเตอร์ \vec{v} ดังรูปข้างต้น
เวกเตอร์ศูนย์
บทนิยาม
เวกเตอร์ศูนย์ (zero vector) คือ เวกเตอร์ที่มีขนาดเป็นศูนย์
เวกเตอร์ศูนย์ เขียนแทนด้วย \vec{0}
โดยทั่วไปเราจะไม่กล่าวถึงทิศทางของเวกเตอร์ศูนย์ แต่ถ้าต้องการกล่าวถึงมีข้อตกลงว่าจะระบุทิศทางของเวกเตอร์ศูนย์เป็นเช่นใดก็ได้
จากบทนิยามจะเห็นว่า สำหรับเวกเตอร์ \vec{u} ใด ๆ \vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u} และ \vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{0}
เวกเตอร์ศูนย์จะมีจุดเริ่มต้นและจุดสิ้นสุดของเวกเตอร์เป็นจุดเดียวกันนั่นเอง
สรุปสมบัติการบวกเวกเตอร์ ได้ดังนี้ \vec{u}
ให้ \vec{u} , \vec{v} และ \vec{w} เป็นเวกเตอร์ใด ๆ
1. \vec{u}+\vec{v} =\vec{v}+\vec{u}
2. (\vec{u}+\vec{v})+\vec{w} =\vec{u}+(\vec{v}+\vec{w})
3. \vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u}
4. \vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{0}
การลบเวกเตอร์
หลังจากเรารู้จักการบวกเวกเตอร์และเวกเตอร์ศูนย์แล้ว ในหัวข้อนี้เราจะมาดูว่าการลบเวกเตอร์ มีหลักการหรือวิธีการที่เหมือนหรือแตกต่างจากการบวกเวกเตอร์ยังไง
บทนิยาม
ให้ \vec{u} และ \vec{v} เป็นเวกเตอร์ใด ๆ \vec{u} ลบด้วย \vec{v} เขียนแทนด้วย \vec{u}-\vec{v} คือผลบวกเวกเตอร์ของ \vec{u} และนิเสธของ \vec{v} นั่นคือ \vec{u}-\vec{v}=\vec{u}+(-\vec{v})
การลบเวกเตอร์สามารถหาได้จากการบวกด้วยนิเสธของเวกเตอร์ นั่นคือการบวกเวกเตอร์นั้นในทิศทางตรงกันข้าม โดยน้อง ๆ สามารถใช้การบวกแบบหางต่อหัวเช่นเดียวกันกับการบวกในหัวข้อก่อนหน้าเลย
ตัวอย่างที่ 2
จงหาเวกเตอร์ \vec{u} – \vec{v}
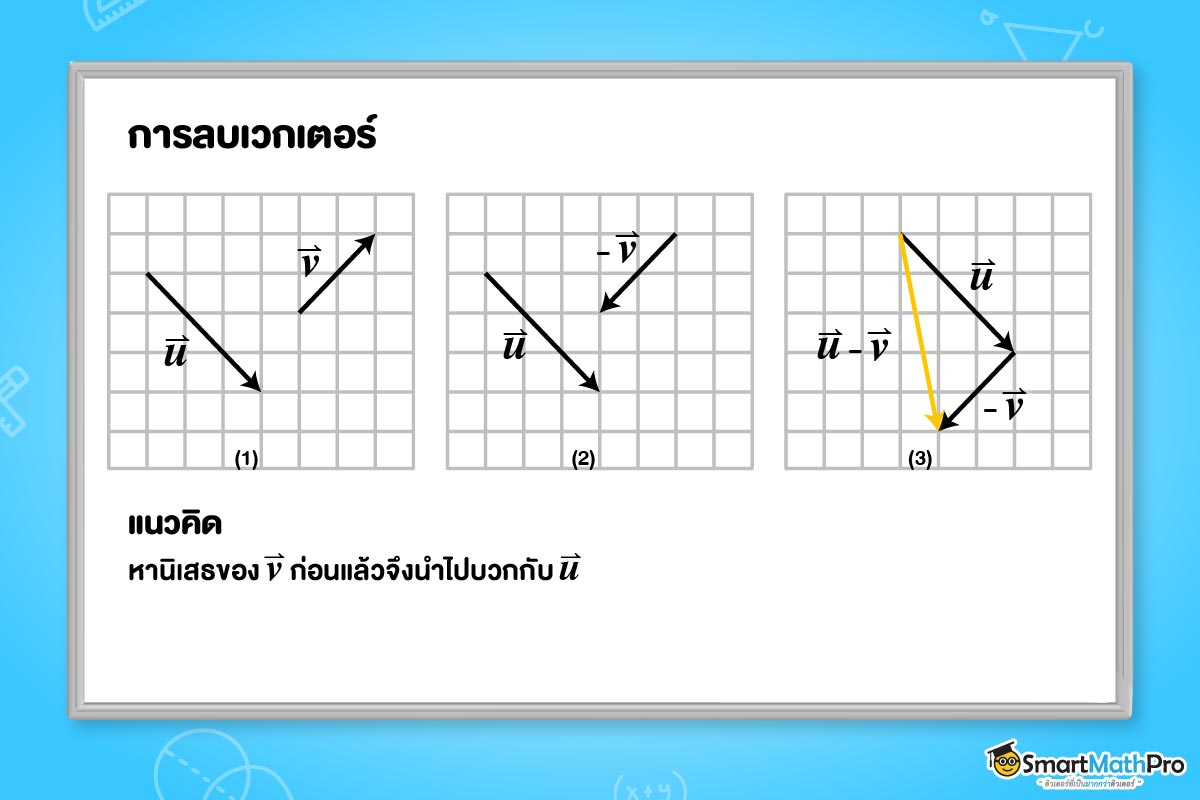
จาก \vec{u} และ \vec{v} ที่กำหนดให้ เราจะหานิเสธของ \vec{v} โดยที่มีขนาดเท่าเดิม แต่มีทิศทางตรงกันข้าม นั่นคือ -\vec{v} จากนั้นนำ \vec{u} มาบวกกับ -\vec{v} แล้วจะได้เวกเตอร์ลัพธ์ที่ลากจากหางของ \vec{u} ไปที่หัวของ -\vec{v} และมีทิศทางดังรูปด้านบน
การคูณเวกเตอร์ด้วยสเกลาร์
ในการศึกษาหัวข้อนี้ เราจะใช้อักษร a, b, c, … แทนสเกลาร์ (จำนวนจริง)
บทนิยาม
ให้ a เป็นสเกลาร์ และ \vec{u} เป็นเวกเตอร์ ผลคูณของ \vec{u} กับสเกลาร์ a เป็นเวกเตอร์ เขียนแทนด้วย a\vec{u} โดยที่
- ถ้า a=0 แล้ว a\vec{u} =\vec{0}
- ถ้า a>0 แล้ว a\vec{u} จะมีขนาด \left |a \right |\left |\vec{u} \right | หน่วย และมีทิศทางเดียวกับ \vec{u}
- ถ้า a<0 แล้ว a\vec{u} จะมีขนาด \left |a \right |\left |\vec{u} \right| หน่วย แต่มีทิศทางตรงข้ามกับ \vec{u}
หมายเหตุ
1. (-1)\vec{u}=-\vec{u}
2. ถ้า a\neq 0 และ \vec{u} ไม่ใช่เวกเตอร์ศูนย์ แล้ว a\vec{u} จะขนานกับ \vec{u}
ตัวอย่างที่ 3
ให้ \vec{u} เป็นเวกเตอร์ที่มีขนาด 4 หน่วย จงบรรยายลักษณะของเวกเตอร์ต่อไปนี้
- 4\vec{u}
- -4\vec{u}
- \frac{1}{4}\vec{u}
- -\frac{1}{4}\vec{u}
- เนื่องจาก 4>0 ดังนั้น 4\vec{u} จะมีขนาดเป็นสี่เท่าของ \vec{u} หรือมีขนาด 16 หน่วย และมีทิศทางเดียวกับ \vec{u}
- เนื่องจาก -4<0 ดังนั้น -4\vec{u} จะมีขนาดเป็นสี่เท่าของ \vec{u} หรือมีขนาด 16 หน่วย แต่มีทิศทางตรงข้ามกับ \vec{u}
- เนื่องจาก \frac{1}{4}>0 ดังนั้น \frac{1}{4}\vec{u} จะมีขนาดเป็นหนึ่งในสี่ของ \vec{u} หรือมีขนาด 1 หน่วย และมีทิศทางเดียวกับ \vec{u}
- เนื่องจาก -\frac{1}{4}<0 ดังนั้น -\frac{1}{4}\vec{u} จะมีขนาดเป็นหนึ่งในสี่ของ \vec{u} หรือมีขนาด 1 หน่วย แต่มีทิศทางตรงข้ามกับ \vec{u}
สรุปสมบัติการคูณเวกเตอร์ด้วยสเกลาร์ ได้ดังนี้
ให้ a, b เป็นสเกลาร์ และ \vec{u}, \vec{v} เป็นเวกเตอร์
- 1\vec{u}=\vec{u}
- a(\vec{u}+\vec{v})=a\vec{u}+a\vec{v}
- (a+b)\vec{u}=a\vec{u}+b\vec{u}
- (ab)\vec{u}=a(b\vec{u})+b(a\vec{u})
เวกเตอร์ในระบบพิกัดฉาก
หลังจากที่น้อง ๆ ได้รู้จักแล้วว่าเวกเตอร์คืออะไร สามารถเขียนสัญลักษณ์แทนเวกเตอร์ได้แบบไหนแล้ว แต่การจะบรรยายว่าเวกเตอร์นั้นมีขนาดเท่าไร และมีทิศทางไปทางไหนโดยใช้การวาดรูปไปตลอดคงจะไม่ค่อยสะดวกนัก จึงมีวิธีการเขียนเวกเตอร์ให้เข้าใจได้ง่ายอยู่ 2 แบบ คือ
1. การใช้เมทริกซ์ช่วย
2. การใช้เวกเตอร์ \vec{i}, \vec{j}, \vec{k} ช่วย โดยที่เวกเตอร์ \vec{i}, \vec{j}, \vec{k} เป็นเวกเตอร์ขนาดหนึ่งหน่วยที่มีทิศทางตามแกน X, Y, Z ในระบบพิกัดฉากตามลำดับ
ซึ่งวิธีการเขียน 2 แบบนี้มีความแตกต่างกันยังไง พี่มีตัวอย่างให้น้อง ๆ ได้ดู ตามนี้เลย
ตัวอย่างที่ 4
จงเขียนเวกเตอร์ \overrightarrow{OP} ที่มีลักษณะดังรูป ในรูปแบบเมทริกซ์ และในรูปแบบเวกเตอร์ \vec{i}, \vec{j}, \vec{k}
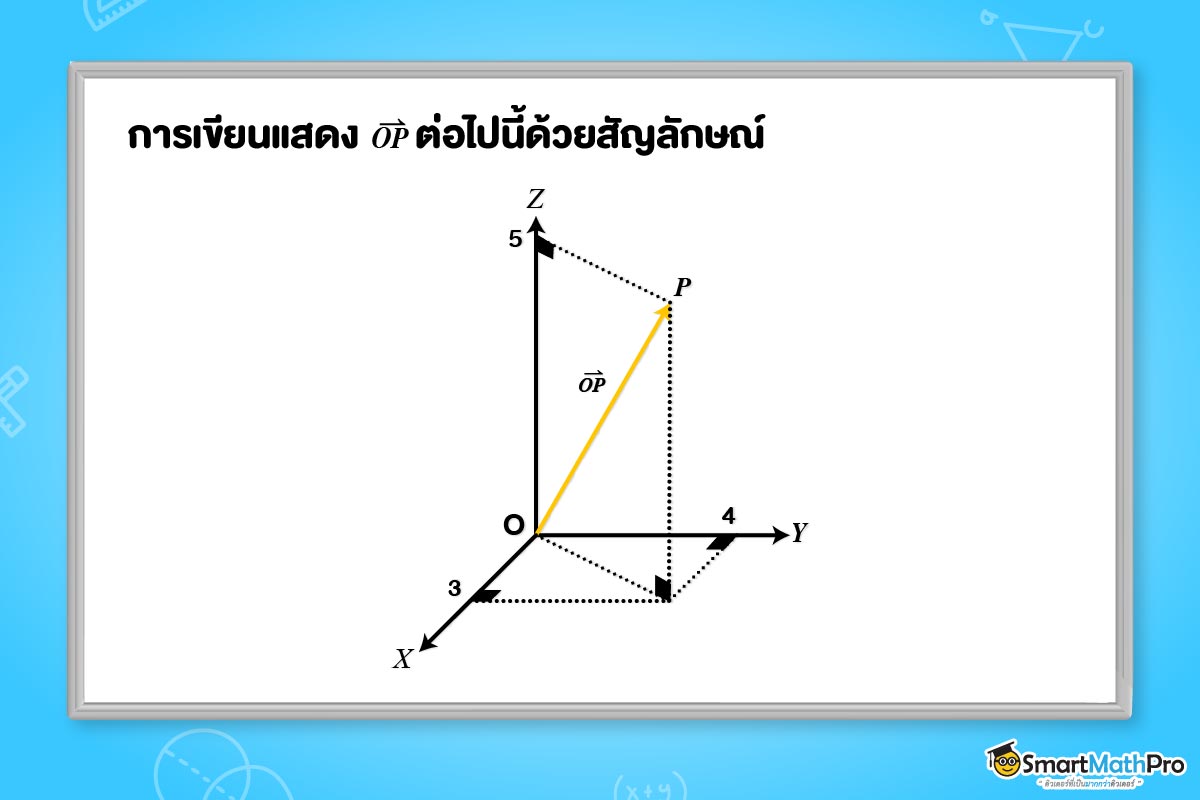
วิธีทำ
- เขียนในรูปแบบเมทริกซ์ \overrightarrow{OP}=\begin{bmatrix}3\\4\\5\end{bmatrix}
- เขียนในรูปแบบเวกเตอร์ \vec{i}, \vec{j}, \vec{k}
\overrightarrow{OP}=3\vec{i}, 4\vec{j}, 5\vec{k}
ป.ล. พี่จะขอใช้วิธีการเขียนเวกเตอร์ในรูปแบบเมทริกซ์ในการอธิบายเนื้อหาหลังจากนี้น้า
โดยตัวอย่างข้างต้นเป็นการหาเวกเตอร์ที่มีจุดเริ่มต้นเป็นจุดกำเนิด แต่ถ้าจุดเริ่มต้นไม่ใช่จุดกำเนิดล่ะ จะหาเวกเตอร์ยังไงดี พี่มีตัวอย่างเล็ก ๆ ที่จะให้น้อง ๆ รู้วิธีหาเวกเตอร์จากจุดเริ่มต้นและจุดสิ้นสุดใด ๆ ได้ ตามนี้เลย
ตัวอย่างที่ 5
จงหาเวกเตอร์ \overrightarrow{AB} และ \overrightarrow{BA} ที่มีจุด A คือจุด \left (3,4 \right ) และจุด B คือจุด \left (5,1 \right )
วิธีทำ
\overrightarrow{AB}=\begin{bmatrix}5-3\\1-4\end{bmatrix}
=\begin{bmatrix} 2\\-3\end{bmatrix}
ดังนั้น \overrightarrow{AB}=\begin{bmatrix} 2\\-3\end{bmatrix}
\overrightarrow{BA}=\begin{bmatrix}3-5\\4-1\end{bmatrix}
=\begin{bmatrix}-2\\ 3\end{bmatrix}
ดังนั้น \overrightarrow{BA}=\begin{bmatrix}-2\\ 3\end{bmatrix}
ตัวอย่างที่ 6
จงหาเวกเตอร์ \overrightarrow{CD} และ \overrightarrow{DC} ที่มีจุด C คือจุด \left (1,-3,7 \right ) และจุด D คือจุด \left (-2,-1,2 \right )
วิธีทำ
\overrightarrow{CD} =\begin{bmatrix} -2 -1\\ -1 -(-3)\\ 2 -7\end{bmatrix}
=\begin{bmatrix}-3\\ 2\\-5\end{bmatrix}
ดังนั้น \overrightarrow{CD}=\begin{bmatrix}-3\\ 2\\-5\end{bmatrix}
\overrightarrow{DC}=\begin{bmatrix} 1 -(-2)\\ -3 -(-1)\\ 7 -2\end{bmatrix}
=\begin{bmatrix} 3\\-2\\ 5\end{bmatrix}
ดังนั้น \overrightarrow{DC}=\begin{bmatrix} 3\\-2\\ 5\end{bmatrix}
ขนาดของเวกเตอร์ในระบบพิกัดฉาก
การหาขนาดของเวกเตอร์ เราจะใช้ความรู้เดิมจากเรื่องเรขาคณิตวิเคราะห์ นั่นคือ ระยะห่างระหว่างจุดกับจุด เช่น ถ้าอยากหาขนาดของ \overrightarrow{AB} เราจะหาระยะห่างระหว่างจุด A กับจุด B และสรุปเป็นขนาดของ \overrightarrow{AB} ได้เลย โดยมีสูตรขนาดของเวกเตอร์ดังนี้
กำหนดให้ \vec{u}=\begin{bmatrix}a\\b\end{bmatrix} และ \vec{v}=\begin{bmatrix}a\\ b\\ c\end{bmatrix} จะได้ว่า
ขนาดของ \vec{u}=\left | \vec{u} \right |=\sqrt{a^{2}+b^{2}}
ขนาดของ \vec{v}=\left |\vec{v} \right |=\sqrt{a^{2}+b^{2}+c^{2}}
ตัวอย่างที่ 7
จงหาขนาดของ \vec{u} โดยที่ \vec{u}=\begin{bmatrix} 2\\ -3\\ 6\end{bmatrix}
วิธีทำ
\left | \vec{u} \right |=\sqrt{2^{2}+(-3)^{2}+6^{2}}
=\sqrt{4+9+36}
=\sqrt{49}
=7
ดังนั้น ขนาดของ \vec{u} คือ =7
เวกเตอร์หนึ่งหน่วยในระบบพิกัดฉาก
บทนิยาม
เวกเตอร์ที่มีขนาดหนึ่งหน่วย เรียกว่า เวกเตอร์หนึ่งหน่วย
เวกเตอร์หนึ่งหน่วยในระบบพิกัดฉาก 2 มิติที่สำคัญคือ \begin{bmatrix}1\\ 0\end{bmatrix} เขียนแทนด้วย \vec{i} และ \begin{bmatrix}0\\ 1\end{bmatrix} เขียนแทนด้วย \vec{j}
ส่วนเวกเตอร์หนึ่งหน่วยที่สำคัญในระบบพิกัดฉาก 3 มิติที่สำคัญ คือ \begin{bmatrix}1\\ 0\\ 0\end{bmatrix} เขียนแทนด้วย \vec{i} , \begin{bmatrix}0\\ 1\\ 0\end{bmatrix} เขียนแทนด้วย \vec{j} และ \begin{bmatrix}0\\ 0\\ 1\end{bmatrix} เขียนแทนด้วย \vec{k}
เนื่องจาก \vec{u} ใด ๆ ที่ไม่ใช่เวกเตอร์ศูนย์จะมีขนาดเท่ากับ \left |\vec{u} \right | ดังนั้นเวกเตอร์หนึ่งหน่วยที่มีทิศทางเดียวกับ \vec{u} คือ \frac{\vec{u}}{\left |\vec{u} \right | }
ตัวอย่างที่ 8
จงหาเวกเตอร์หนึ่งหน่วยที่มีทิศทางเดียวกับ \begin{bmatrix}-4\\ 8\\ -1\end{bmatrix}
วิธีทำ
\left | \vec{u} \right |=\sqrt{(-4)^{2}+(8)^{2}+(-1)^{2}}
=\sqrt{16+64+1}
=\sqrt{81}
=9
\frac{\vec{u}}{\left |\vec{u}\right |}=\frac{1}{9}\begin{bmatrix}-4\\ 8\\-1\end{bmatrix}
=\begin{bmatrix}-\frac{4}{9}\\\\ \frac{8}{9}\\\\-\frac{1}{9}\end{bmatrix}
ดังนั้น เวกเตอร์หนึ่งหน่วยที่มีทิศทางเดียวกับ \begin{bmatrix}-4\\ 8\\-1\end{bmatrix} คือ \begin{bmatrix}-\frac{4}{9}\\\\ \frac{8}{9}\\\\-\frac{1}{9}\end{bmatrix}
การดำเนินการของเวกเตอร์
ตัวอย่างที่ 9
กำหนดให้ \vec{u}=\begin{bmatrix}-3\\ 5\end{bmatrix} และ \vec{v}=\begin{bmatrix} 4\\ -6\end{bmatrix} จงหา 2\vec{u}-\vec{v}
วิธีทำ
2\vec{u}-\vec{v}=2\begin{bmatrix}-3\\ 5\end{bmatrix}-\begin{bmatrix} 4\\-6\end{bmatrix}
=\begin{bmatrix}-6\\ 10\end{bmatrix}-\begin{bmatrix} 4\\-6\end{bmatrix}
=\begin{bmatrix}-6 -4\\ 10 -(-6)\end{bmatrix}
=\begin{bmatrix}-10\\ 16\end{bmatrix}
ดังนั้น 2\vec{u}-\vec{v}=\begin{bmatrix}-10\\ 16\end{bmatrix}
ผลคูณเชิงสเกลาร์
บทนิยาม
ให้ \vec{u} และ \vec{v} เป็นเวกเตอร์ในระบบพิกัดฉากสองมิติหรือสามมิติ a_{1},a_{2},a_{3},b_{1},b_{2} และ b_{3} เป็นสเกลาร์ ผลคูณเชิงสเกลาร์ของ \vec{u} และ \vec{v} (อ่านว่า เวกเตอร์ยู ดอท เวกเตอร์วี) กำหนดดังนี้
- ถ้า \vec{u}=a_{1}\vec{i}+a_{2}\vec{j} และ \vec{v} = b_{1}\vec{i}+b_{2}\vec{j} เป็นเวกเตอร์ในระบบพิกัดฉากสองมิติ จะได้ \vec{u}\cdot \vec{v}=a_{1}b_{1}+a_{2}b_{2}
- ถ้า \vec{u}=a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k} และ \vec{v}=b_{1}\vec{i}+b_{2}\vec{j}+b_{3}\vec{k} เป็นเวกเตอร์ในระบบพิกัดฉากสามมิติ
จะได้ \vec{u}\cdot \vec{v}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}
ตัวอย่างที่ 10
กำหนดให้ \vec{u}=\begin{bmatrix}-3\\ 5\end{bmatrix} และ \vec{v}=\begin{bmatrix} 4\\ -6\end{bmatrix} จงหา \vec{u}\cdot \vec{v}
วิธีทำ
\vec{u}\cdot \vec{v}=(-3)(4)+(5)(-6)
=(-12)+(-30)
=-42
ดังนั้น \vec{u}\cdot \vec{v}=-42
ให้ \vec{u},\vec{v} และ \vec{w} เป็นเวกเตอร์ใด ๆ ในระบบพิกัดฉากสองมิติหรือสามมิติและ a เป็นสเกลาร์ จะได้ว่า
- \vec{u}\cdot \vec{v}=\vec{v}\cdot \vec{u}
- \vec{u}\cdot (\vec{v}+\vec{w})=\left(\vec{u}\cdot\vec{v} \right)+\left(\vec{u}\cdot\vec{w} \right) และ \left(\vec{u}+\vec{v}\right)\cdot \vec{w}=\left(\vec{u}\cdot \vec{w} \right)+\left(\vec{v}\cdot \vec{w} \right)
- a\left(\vec{u}\cdot \vec{v} \right)=\left (a\vec{u}\right)\cdot \vec{v}=\vec{u}\cdot \left (a\vec{v}\right)
- \vec {0}\cdot \vec{u}=0
- \vec {u}\cdot \vec{u}=\left | \vec{u} \right |^{2}
- \vec{i}\cdot \vec{i}=\vec {j}\cdot \vec{j}=\vec{k}\cdot \vec{k}=1 และ \vec{i}\cdot \vec {j}=\vec{i}\cdot \vec{k}=\vec{j}\cdot \vec{k}=0
ให้ \vec{u} และ \vec{v} เป็นเวกเตอร์ใด ๆ ที่ไม่ใช่เวกเตอร์ศูนย์ ในระบบพิกัดฉากสองมิติหรือสามมิติและ \theta เป็นขนาดของมุมระหว่าง \vec{u} และ \vec{v} ซึ่ง 0^{\circ}\leq \theta \leq 180^{\circ} (มุมระหว่างเตอร์ หมายถึงที่ไม่ใช่มุมกลับ ซึ่งมีแขนของมุมเป็นรังสีที่ขนานและมีทิศทางเดียวกับเวกเตอร์ทั้งสอง) จะได้ว่า
\vec {u}\cdot \vec{v}=\left | \vec{u} \right |\left | \vec{v} \right |\cos \theta
ตัวอย่างที่ 11
จงหาค่าของ \vec{u}\cdot \vec{v} โดยกำหนดให้ขนาดของ \vec{u} และ \vec{v} เป็น 10 และ 7 ตามลำดับ และมีขนาดของมุมระหว่างเวกเตอร์ทั้งสองเป็น 90^{\circ}
วิธีทำ
\vec{u}\cdot \vec{v}=\left | \vec{u} \right |\left | \vec{v} \right |cos\theta
=(10)(70)cos90^{\circ}
=(70)(0)
=0
ดังนั้น \vec{u}\cdot \vec{v}=0
จากตัวอย่างข้างต้น พี่อยากให้น้อง ๆ สังเกตว่า ถ้าเวกเตอร์ทั้งสองตั้งฉากกันหรือทำมุมกัน 90^{\circ} จะทำให้ค่าของ \vec{u}\cdot \vec{v} เป็น 0
ให้ \vec{u} และ \vec{v} เป็นเวกเตอร์ใด ๆ ในระบบพิกัดฉากสองมิติหรือสามมิติ จะได้ว่า \vec{u} ตั้งฉากกับ \vec{v} ก็ต่อเมื่อ \vec{u}\cdot \vec{v}=0
ผลคูณเชิงเวกเตอร์
ในหัวข้อที่แล้วน้อง ๆ ได้รู้จักกับผลคูณเชิงสเกลาร์ซึ่งเกิดจากการคูณระหว่างเวกเตอร์สองเวกเตอร์แล้วได้ผลลัพธ์เป็น
สเกลาร์กันไปแล้ว ในหัวข้อนี้จะกล่าวถึงการคูณระหว่างเวกเตอร์สองเวกเตอร์แล้วได้ผลลัพธ์เป็นเวกเตอร์ดูบ้าง
ดังบทนิยามนี้
บทนิยาม
ผลคูณเชิงเวกเตอร์ของ \vec{u} และ \vec {v} เขียนแทนด้วย \vec{u}\times\vec{v}
กำหนดโดย \vec{u}\times \vec{v}= (a_{2}b_{3}-a_{3}b_{2})\vec{i}-(a_{1}b_{3}-a_{3}b_{1})\vec{j}+(a_{1}b_{2}-a_{2}b_{1})\vec{k}
\vec{u}\times\vec {v} อ่านว่า เวกเตอร์ยู ครอส เวกเตอร์วี
วิธีการหาผลคูณเชิงเวกเตอร์ (การครอสเวกเตอร์)
วิธีการครอสเวกเตอร์
\vec{u}\times\vec{v}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\\end{vmatrix}
=\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}\vec{i}-\begin{vmatrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{vmatrix}\vec{j}+\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}\vec{k}
=(a_{2}b_{3}-a_{3}b_{2})\vec{i}-(a_{1}b_{3}-a_{3}b_{1})\vec{j}+(a_{1}b_{2}-a_{2}b_{1})\vec{k}
วิธีทำ
\vec{u}\times\vec{v}=\begin{vmatrix}\vec{i}\:\:\vec{j}\:\:\vec{k}\\2\:\:3\:\:0\\
1\:\:2\:\:3\\\end{vmatrix}
=\begin{vmatrix}3\:0\\2\:3\end{vmatrix}\vec{i}-\begin{vmatrix}2\:0\\1\:3\end{vmatrix}\vec{j}+\begin{vmatrix}2\:3\\1\:2\end{vmatrix}\vec{k}+
=(9-0)\vec{i}-(6-0)\vec{j}+(4-3)\vec{k}
=9\vec{i}-6\vec{j}+\vec{k}
ทีนี้มาดูหน้าตาของเวกเตอร์ที่ได้จากการ “ครอส” กันเถอะ !!
ลักษณะของผลลัพธ์ของผลคูณเชิงเวกเตอร์
เราสามารถแสดงทิศทางของ \vec{u}\times\vec{v} โดยใช้กฎของมือขวาได้ดังรูป
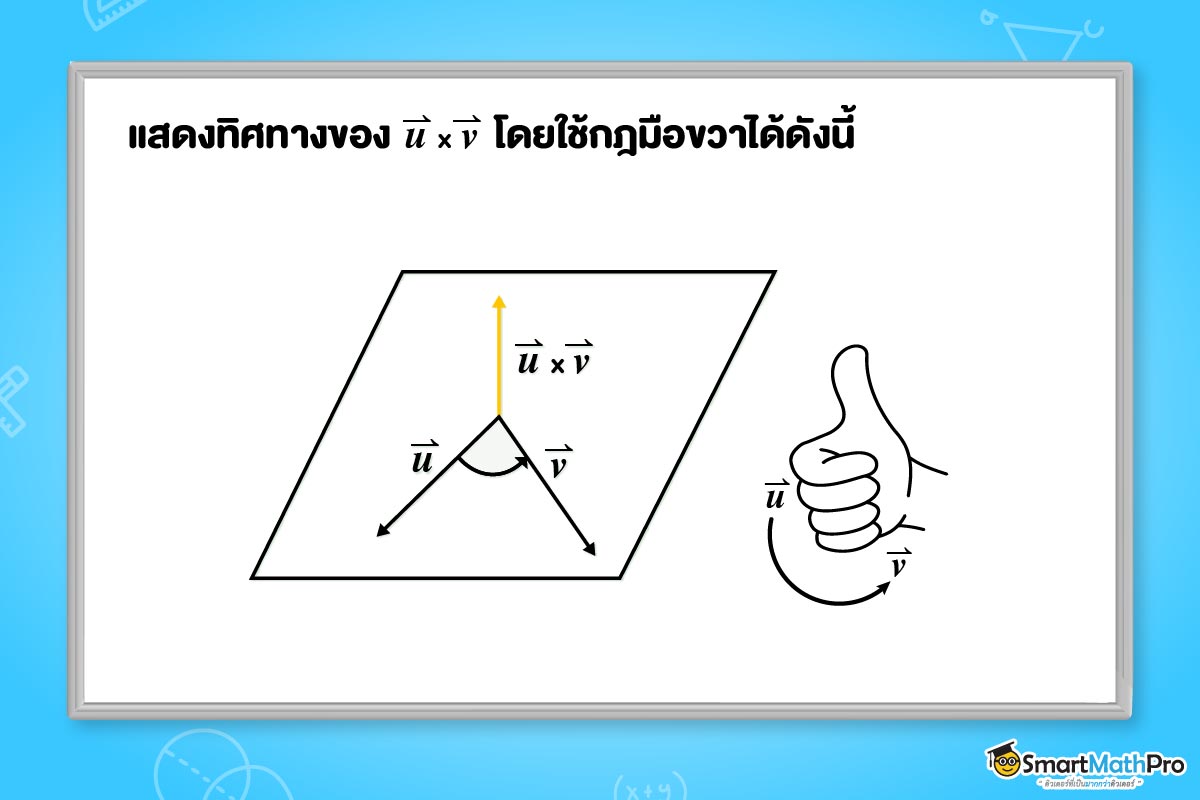
และสามารถแสดงทิศทางของ \vec{v}\times\vec{u} โดยใช้กฎของมือขวาได้ดังรูป
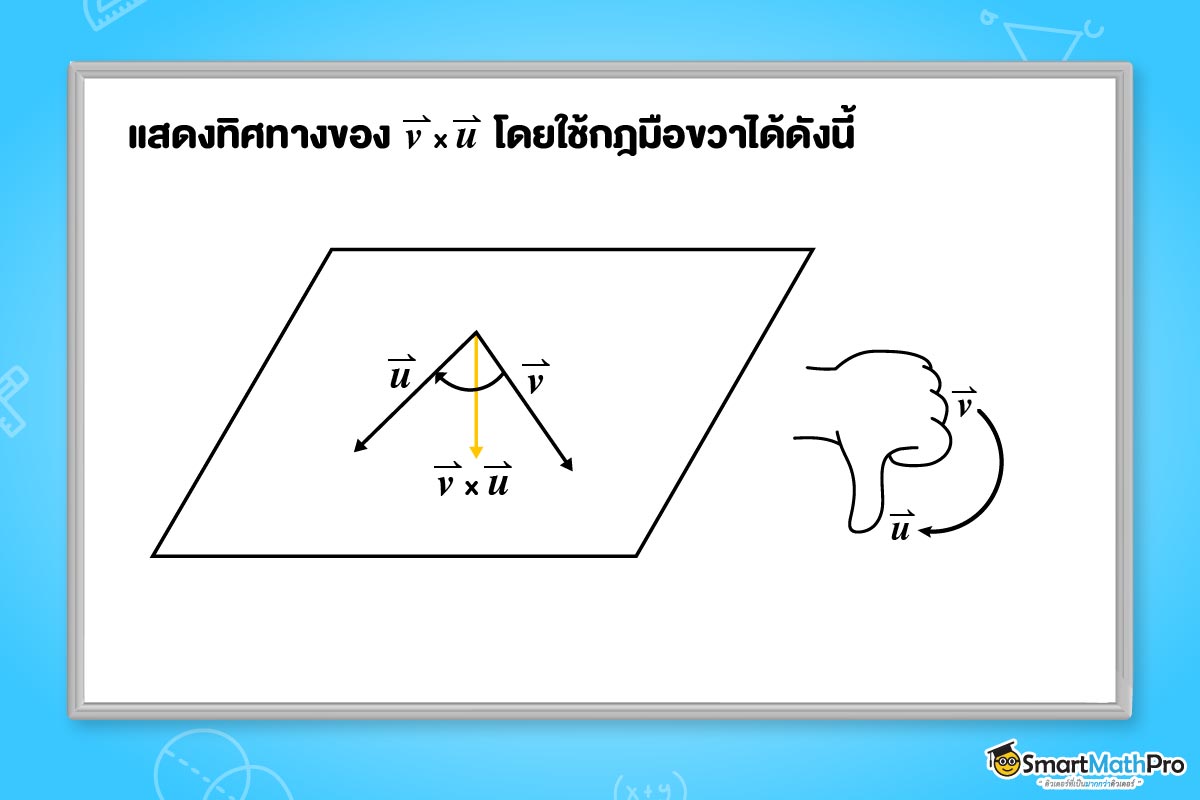
จะสังเกตได้ว่า เมื่อ \vec{u} และ \vec{v} เป็นเวกเตอร์ที่ไม่ขนานกัน จะได้ว่าทั้ง
\vec{u}\times\vec{v} และ \vec{v}\times\vec{u} เป็นเวกเตอร์ที่ตั้งฉากกับระนาบของ \vec{u} และ \vec{v} และทั้งสองมีทิศทางตรงกันข้ามกัน
จึงสรุปได้ว่า \vec{u}\times\vec{v}=-(\vec{v}\times\vec{u}) หรือก็คือเป็นนิเสธของกันและกันนั่นเอง
สมบัติต่าง ๆ ของผลคูณเชิงเวกเตอร์
ให้ \vec{u}, \vec{v} และ \vec{w} เป็นเวกเตอร์ใด ๆ ในระบบพิกัดฉากสามมิติ และ a เป็นจํานวนจริงใด ๆ b
1. \vec{u}\times\vec{v}=-(\vec{v}\times\vec{u})
2. (\vec{u}+\vec{v})\times\vec {w}=(\vec{u}\times\vec {w})+(\vec{v}\times\vec{w})
3. \vec{u}\times(\vec{v}+\vec{w})=(\vec{u}\times\vec{v})+(\vec{u}\times\vec{w})
4. \vec{u}\times (a\vec{v})=a(\vec{u}\times\vec{v})
5. (a\vec{u})\times (\vec{v})=a(\vec{u}\times\vec{v})
6. \vec{u}\times\vec{u} =\vec{0}

น้อง ๆ ได้รู้จักหน้าตาและทิศทางของผลคูณเชิงเวกเตอร์กันแล้ว คราวนี้เหลือขนาดของผลคูณเชิงเวกเตอร์ที่เรายังไม่รู้ ไปดูกันดีกว่าว่าเราจะหาขนาดของผลคูณเชิงเวกเตอร์ได้ยังไง
ให้ \vec{u} และ \vec{v} เป็นเวกเตอร์ใด ๆ ในระบบพิกัดฉากสามมิติ จะได้ว่า \vec{u}\times\vec{v} เป็นเวกเตอร์ที่ตั้งฉากกับ \vec{u} และ \vec{v}
และมีขนาดเป็น \left | \vec{u}\times \vec{v} \right |=\left |\vec{u} \right |\left |\vec{v} \right |\sin \theta
เมื่อ \theta เป็นขนาดของมุมระหว่าง \vec{u} และ \vec{v} โดยที่
0^{\circ }\leq \theta\leq 180^{\circ }
ตัวอย่างที่ 13
ให้ \vec{u}=\begin{bmatrix}1\\2\\0\end{bmatrix} และ \vec{v}=\begin{bmatrix}1\\1\\-2\end{bmatrix} จงหาค่าของ \sin \theta เมื่อ \theta เป็นขนาดของมุมระหว่าง \vec{u} และ \vec{v}
วิธีทำ
\vec{u}\times\vec{v}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\1&2&0\\ 1&1&-2\\\end{vmatrix}
=\begin{vmatrix}2&0\\1&-2\end{vmatrix}\vec{i}-\begin{vmatrix}1&0\\1&-2\end{vmatrix}\vec{j}+\begin{vmatrix}1&2\\1&1\end{vmatrix}\vec{k}
=(-4-0)\vec{i}-(-2-0)\vec{j}+(1-2)\vec{k}
=-4\vec{i}+2\vec{j}-\vec{k}
\left |\vec{u}\times\vec{v}\right|=\sqrt{(-4)^{2}+(2)^{2}+(-1)^{2}}=\sqrt{21}
\left |\vec{u}\right|=\sqrt{1^{2}+2^{2}+0^{2}}=\sqrt{5}
\left |\vec{v}\right|=\sqrt{1^{2}+1^{2}+(-2)^{2}}=\sqrt{6}
เนื่องจาก \left |\vec{u}\right|\neq0,\left |\vec{v}\right|\neq0 และ \left |\vec{u}\times\vec{v}\right|=\left |\vec{u}\right|\left |\vec{v}\right|sin\theta
จะได้ว่า sin\theta=\frac{\left |\vec{u}\times\vec{v}\right|}{\left |\vec{u}\right|\left |\vec{v}\right|}
ดังนั้น sin\theta=\frac{\sqrt{21}}{\sqrt{5}\sqrt{6}}=\sqrt{\frac{21}{30}}=\sqrt{\frac{7}{10}}=\frac{\sqrt{70}}{10}
การหาพื้นที่และปริมาตร
การใช้เวกเตอร์ในการหาพื้นที่ของรูปสี่เหลี่ยมด้านขนาน
ก่อนอื่น ขอทบทวนเรื่องตรีโกณมิติกันนิดนึงน้า ถ้าเรามีรูปสามเหลี่ยมมุมฉากที่มุมหนึ่งมีขนาด \theta และด้านตรงข้ามมุมฉากยาว a เราจะได้ว่าด้านประชิดมุมและด้านตรงข้ามมุมจะมีความยาวเป็น a\cos \theta และ a\sin\theta ดังรูป
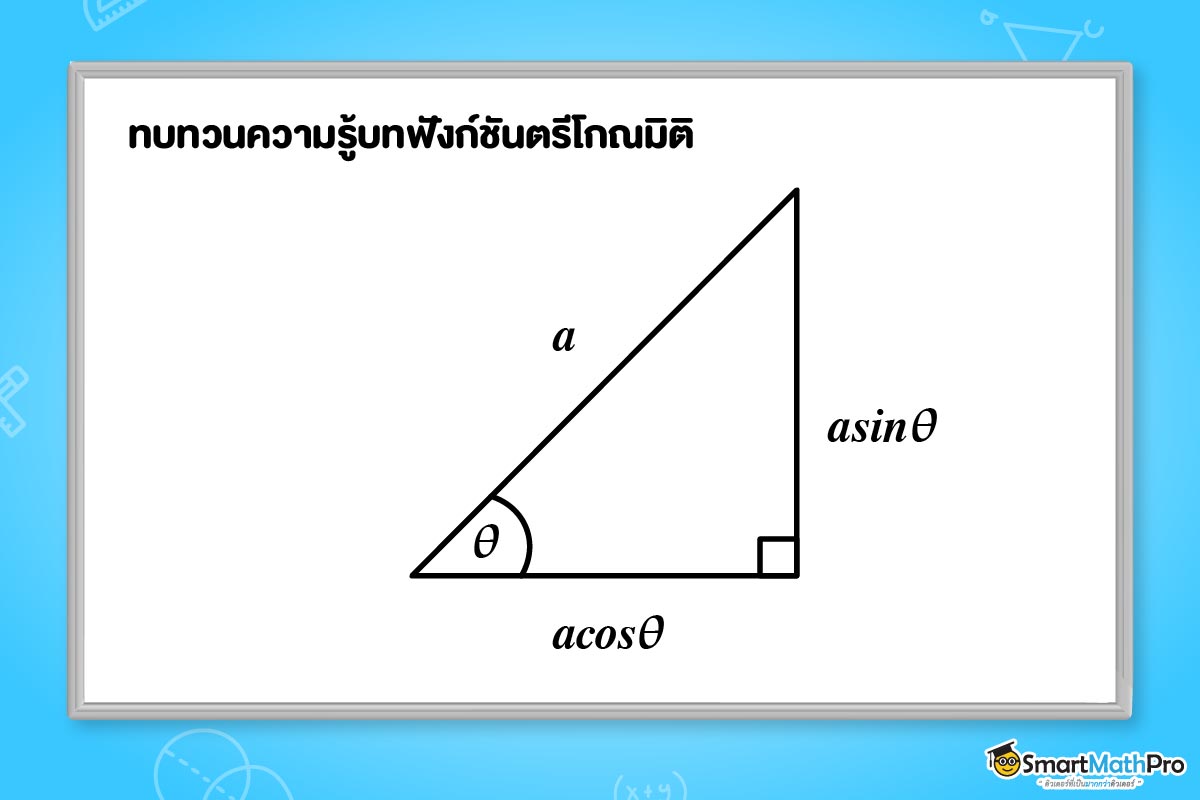
เนื่องจาก ขนาดของเวกเตอร์สามารถแทนด้วยความยาวของเวกเตอร์ในรูปของลูกศรได้ แสดงว่า เราสามารถนำความยาวดังกล่าวมาใช้ในการหาพื้นที่ของรูปสี่เหลี่ยมด้านขนานได้ ว่าแต่เราจะประยุกต์ยังไง น้อง ๆ ไปดูกันเลย
กำหนดรูปสี่เหลี่ยมด้านขนาน ABCD
ให้ \vec{u}=\overrightarrow{AB},\vec{v}=\overrightarrow {AD} และ \theta เป็นขนาดของมุมระหว่าง \vec{u} และ \vec{v}
สิ่งที่เราต้องการคือพื้นที่ของสี่เหลี่ยมด้านขนาน ซึ่งมีสูตรว่า ฐาน \times สูง
โจทย์กำหนดเวกเตอร์มาให้เพียงอย่างเดียว เราต้องนำเวกเตอร์ที่มีไปหาขนาดก่อนเพื่อไปหาความยาวของด้านต่าง ๆ ต่อได้ โดยเราจะได้ว่าความยาวของฐานสี่เหลี่ยมด้านขนานเท่ากับ \left |\vec{u} \right | ส่วนความสูงของสี่เหลี่ยมนั้น จากความรู้ตรีโกณมิติที่ทบทวนไปข้างต้นก็จะได้ว่าความสูงของรูปสี่เหลี่ยมด้านขนานเท่ากับ \left |\vec{v} \right |\sin \theta ดังรูป
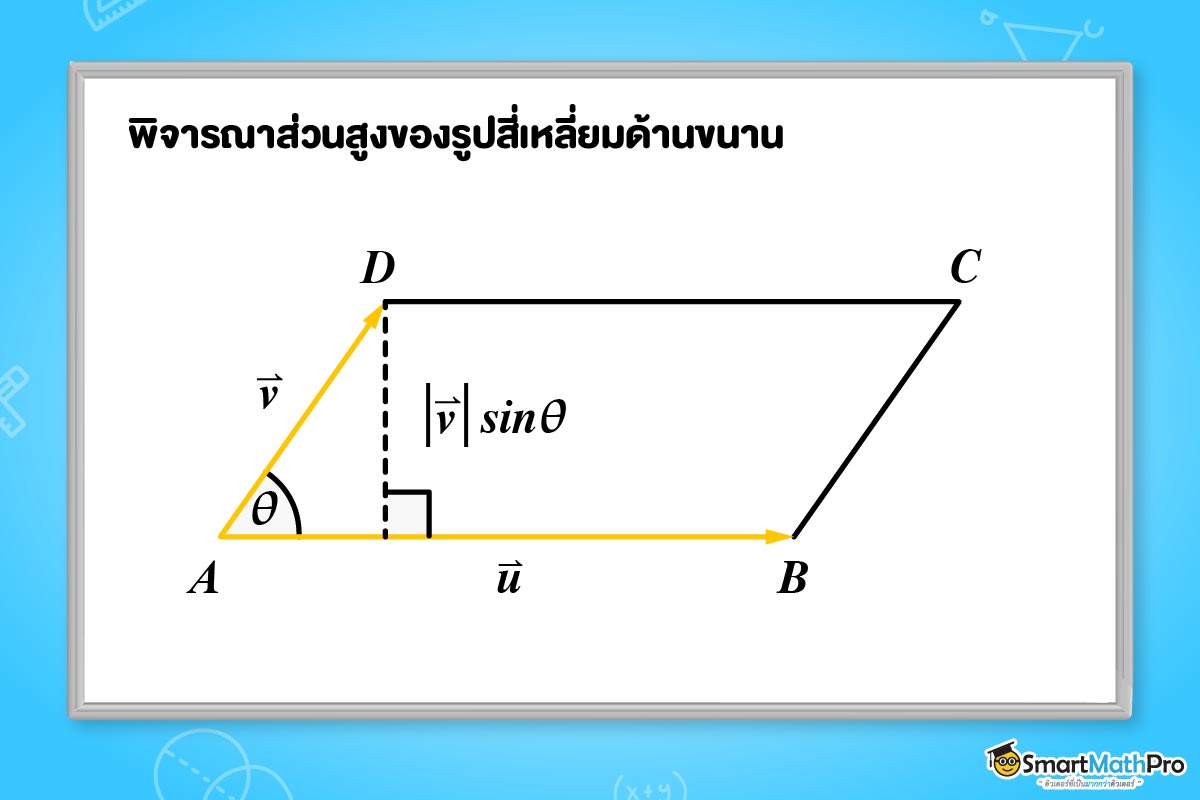
จึงสรุปได้ว่า \left |\vec{u} \right |\left |\vec{v} \right |\sin \theta เป็นพื้นที่ของรูปสี่เหลี่ยมด้านขนาน
แต่เนื่องจาก \left | \vec{u}\times \vec{v} \right |=\left |\vec{u} \right |\left |\vec{v} \right |\sin \theta
ดังนั้น \left | \vec{u}\times \vec{v} \right | จึงเป็นพื้นที่ของสี่เหลี่ยมด้านขนานดังกล่าวด้วย
ตัวอย่างที่ 14
จงหาพื้นที่ของรูปสี่เหลี่ยมด้านขนาน ABCD เมื่อ \overrightarrow{AB}=2\vec{i}+\vec{j}+5\vec{k} และ \overrightarrow{AD}=-\vec{i}+2\vec{j}+3\vec{k}
วิธีทำ พื้นที่สี่เหลี่ยมด้านขนาน ABCD เท่ากับ \left |\vec{AB}\right |\times \left |\vec{AD}\right | เนื่องจาก
\vec{AB}\times\vec{AD}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\2&1&5\\-1&2&3\\\end{vmatrix}
=\begin{vmatrix}1&5\\2&3\end{vmatrix}\vec{i}-\begin{vmatrix}2&5\\-1&3\end{vmatrix}\vec{j}+\begin{vmatrix}2&1\\-1&2\end{vmatrix}\vec{k}
=(3-10)\vec{i}-(6-(-5))\vec{j}+(4-(-1))\vec{k}
=-7\vec{i}-11\vec{j}+5\vec{k}
จะได้ \left |\vec{AB}\times\vec{AD}\right |=\sqrt{(-7)^{2}+(11)^{2}+(5)^{2}}=\sqrt{195}
ดังนั้น รูปสี่เหลี่ยมด้านขนาน ABCD มีพื้นที่ \sqrt{195} ตารางหน่วย
การใช้เวกเตอร์ในการหาปริมาตรของทรงสี่เหลี่ยมด้านขนาน
กำหนดทรงสี่เหลี่ยมด้านขนาน ABCDEFGH ให้ \vec{u}=\overrightarrow{AB},\vec{v}=\overrightarrow{AD},\vec{w}=\overrightarrow{AF} และ \theta เป็นขนาดของมุมระหว่าง \vec{u} และ \vec{v}\times \vec{w} ในที่นี้จะพิจารณารูปสี่เหลี่ยมด้านขนาน ADEF เป็นฐาน และ h เป็นความสูง จะได้ว่า h=\left | \vec{u} \right |\left |\cos \theta\right | ดังรูป
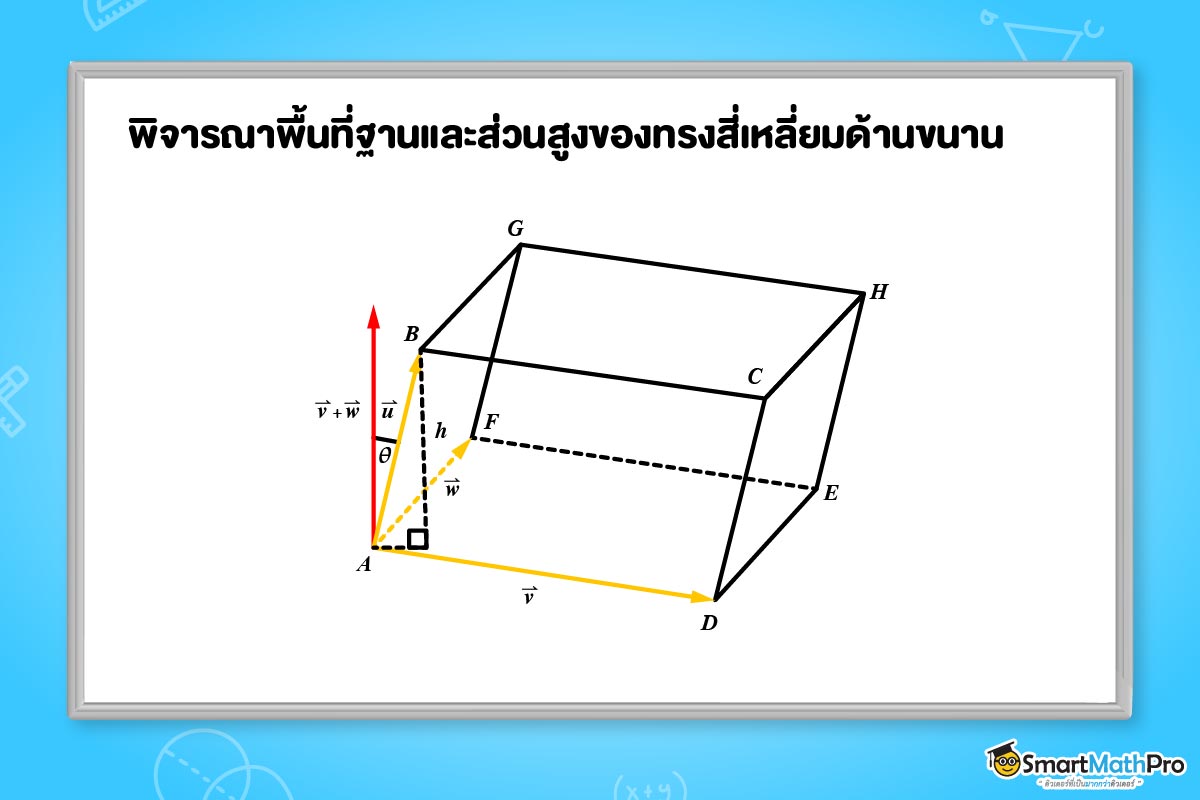
จากสูตรการหาปริมาตรทางสี่เหลี่ยมขนานนั่นคือ พื้นที่ฐาน x สูง
ดังนั้น ปริมาตรของทรงสี่เหลี่ยมขนานเท่ากับ \left |\vec{v}\times\vec{w}\right |\left |\vec{u} \right |\left | cos\theta \right |=|\left |\vec{u} \right |\left |\vec{v}\times\vec{w}\right |\left | cos\theta \right |
เนื่องจาก \vec{u}\cdot\vec{v}=\left |\vec{u} \right |\left |\vec{v} \right |cos\theta จึงได้ \left |\vec{u}\cdot(\vec{v}\times\vec{w})\right | (ที่มีการใส่เครื่องหมายค่าสัมบูรณ์ \left |… \right | ครอบไว้ทั้งหมด เพราะปริมาตรไม่สามารถเป็นจำนวนจริงลบได้)
ตัวอย่างที่ 15
จงหาปริมาตรของทรงสี่เหลี่ยมด้านขนาน ABCDEFGH โดยที่ \overrightarrow{AB}=\vec{u}=\vec{i}+2\vec{k},\overrightarrow{AD}=\vec{v}=2\vec{j}+\vec{k} และ \overrightarrow{AF}=\vec{w}=\vec{i}+2\vec{j}
วิธีทำ เนื่องจากปริมาตรทรงสี่เหลี่ยมด้านขนานเท่ากับ \left |\vec{u}\cdot(\vec{v}\times\vec{w})\right |
\vec{u}\times\vec{w}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\0&2&1\\ 1&2&0\\\end{vmatrix}
=\begin{vmatrix}2&1\\2&0\end{vmatrix}\vec{i}-\begin{vmatrix}0&1\\1&0\end{vmatrix}\vec{j}+\begin{vmatrix}0&2\\1&2\end{vmatrix}\vec{k}
=(0-2)\vec{i}-(0-1)\vec{j}+(0-2)\vec{k}
=-2\vec{i}+\vec{j}-2\vec{k}
จะได้ \left |\vec{u}\cdot(\vec{v}\times\vec{w})\right|=\left |(\vec{i}+2\vec{k})\cdot(-2\vec{i}+\vec{j}-2\vec{k})\right |
=\left | (1)(-2)+(0)(1)+(2)(-2)\right |=\left |-2-4 \right |=6
ดังนั้น ปริมาตรของทรงสี่เหลี่ยมด้านขนาน ABCDEFGH เท่ากับ 6 ลูกบาศก์หน่วย
ดูคลิปติวเรื่อง เวกเตอร์
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
อ่านมาจนถึงตรงนี้ พี่่ว่าน้อง ๆ น่าจะพอเห็นภาพรวมเนื้อหาบท เวกตอร์ ม.5 กันบ้างแล้ว ซึ่งนอกจากการอ่านสรุปและลองทำโจทย์ตามตัวอย่างที่พี่ยกมาข้างต้น พี่ก็แนะนำให้ทุกคนลองทำแบบฝึกหัดบทเวกเตอร์เพิ่มเติมด้วยน้าา เราจะได้เข้าใจเนื้อหามากขึ้น พร้อมลุยกับการสอบทั้งกลางภาคและปลายภาคนั่นเองง
แต่ถ้าใครฝึกทำโจทย์เองแล้ว ยังคงมีจุดที่ไม่เข้าใจอยู่ อยากได้คนช่วยไกด์เรื่องเนื้อหาและฝึกทำโจทย์บทเวกเตอร์ รวมถึงเนื้อหาคณิตศาสตร์ ม.ปลาย บทอื่น ๆ ด้วย พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เพราะแพ็กม.5 – ม.6 เรียนได้ถึง 2 ปี และแพ็ก ม.4 – ม.6 เรียนได้ถึง 3 ปี พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมาก นอกจากนี้ยังพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ และถ้าแพ็กไม่ตรงกับบทที่โรงเรียนสอนก็สามารถเลือกเป็นคอร์สแยกบทได้เพราะมีคอร์สติวแยกบทของคณิต ม.ปลายทุกบทเลย แน่นอนว่ามีส่วนลดพิเศษเช่นกันน้า ใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro























