พอพูดถึงชื่อ ตรีโกณมิติ หลายคนคงจะนึกถึงเนื้อหาที่เคยเรียนผ่านกันมาแล้วตอน ม.3 ใช่ไหมม คราวนี้น้อง ๆ จะได้กลับมาเรียนบทนี้กันอีกครั้งในคณิต ม.5 กับเรื่อง “ฟังก์ชันตรีโกณมิติ” ที่เนื้อหายากขึ้น แต่ไม่ต้องกังวลน้าา เพราะพี่ทำสรุปเนื้อหาของเรื่องนี้มาให้ทุกคนแล้วววว แถมยังมีสรุปสูตรที่ควรรู้สำหรับบทฟังก์ชันตรีโกณมิติ ม.5 รวมถึงตัวอย่างโจทย์และคลิปติวฟรีให้ทุกคนได้อัปคะแนนสอบกัน !!
การวัดมุม
หน่วยในการวัดมุมที่น้อง ๆ รู้จักกันแล้วจากการเรียนบทอัตราส่วนตรีโกณมิติในระดับม.3 คือ องศา (degree) เขียนแทนสัญลักษณ์ ^\circ เช่น 0^{\circ}, 60^{\circ}, 135^{\circ}, 360^{\circ} เป็นต้น
หน่วยวัดมุมที่สำคัญอีกหน่วยหนึ่ง คือ เรเดียน (radian)
มุมที่จุดศูนย์กลางของวงกลมรัศมียาว r หน่วย ซึ่งรองรับด้วยส่วนโค้งของวงกลมที่ยาว a หน่วย มีขนาดเท่ากับ \frac{a}{r} เรเดียน และถ้าให้ขนาดของมุมดังกล่าวเป็น \theta เรเดียน จะได้ \theta = \frac{a}{r}
เนื่องจากมุมที่จุดศูนย์กลางของวงกลมที่มีรัศมียาว r หน่วย มีขนาด 2\pi เรเดียนหรือ 360 องศา
ดังนั้นจึงสรุปได้ว่า
180 องศา เท่ากับ \pi เรเดียน
เปล่ียนมุมในหน่วยเรเดียนเป็นองศา
ฟังก์ชันตรีโกณมิติของมุมของรูปสามเหล่ียมมุมฉาก
ความรู้เดิมในระดับชั้น ม.3 ที่จะถูกนำมาต่อยอดในระดับชั้นนี้คือ อัตราส่วนตรีโกณมิติ กล่าวถึงอัตราส่วนของความยาวด้านของรูปสามเหล่ียมมุมฉาก 6 แบบ ดังนี้
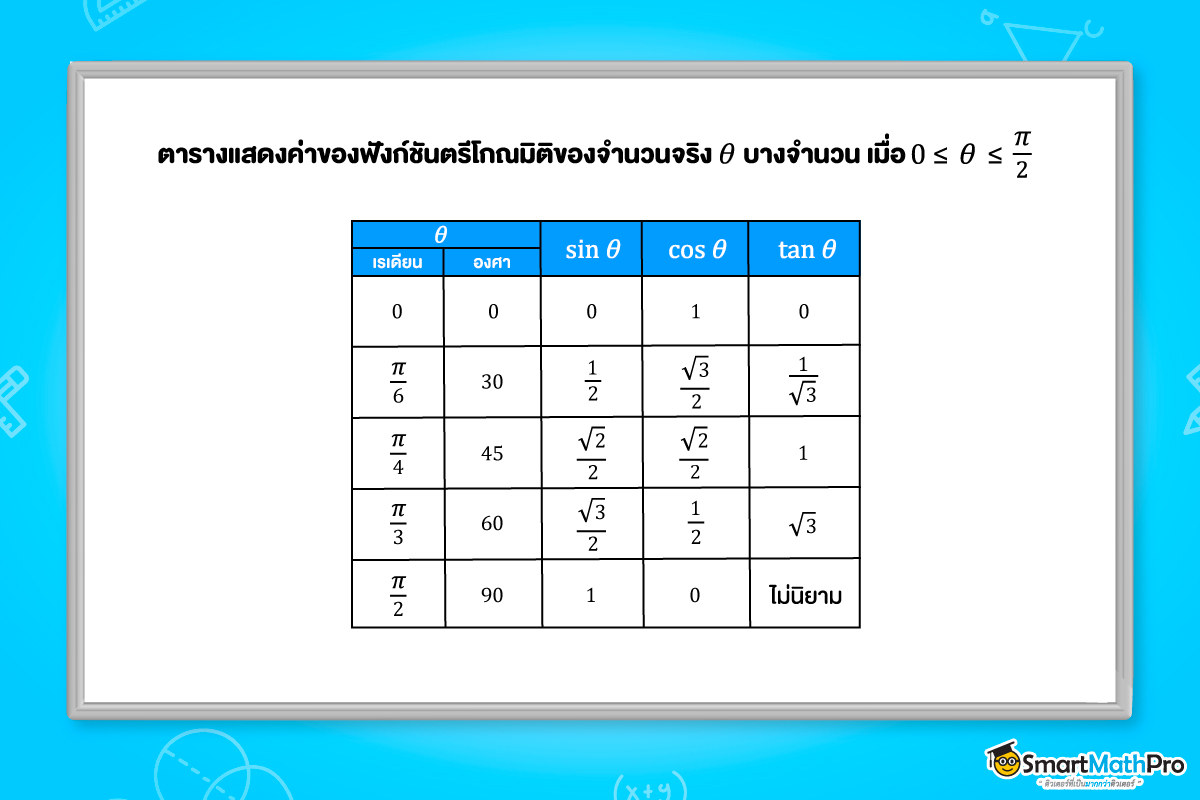
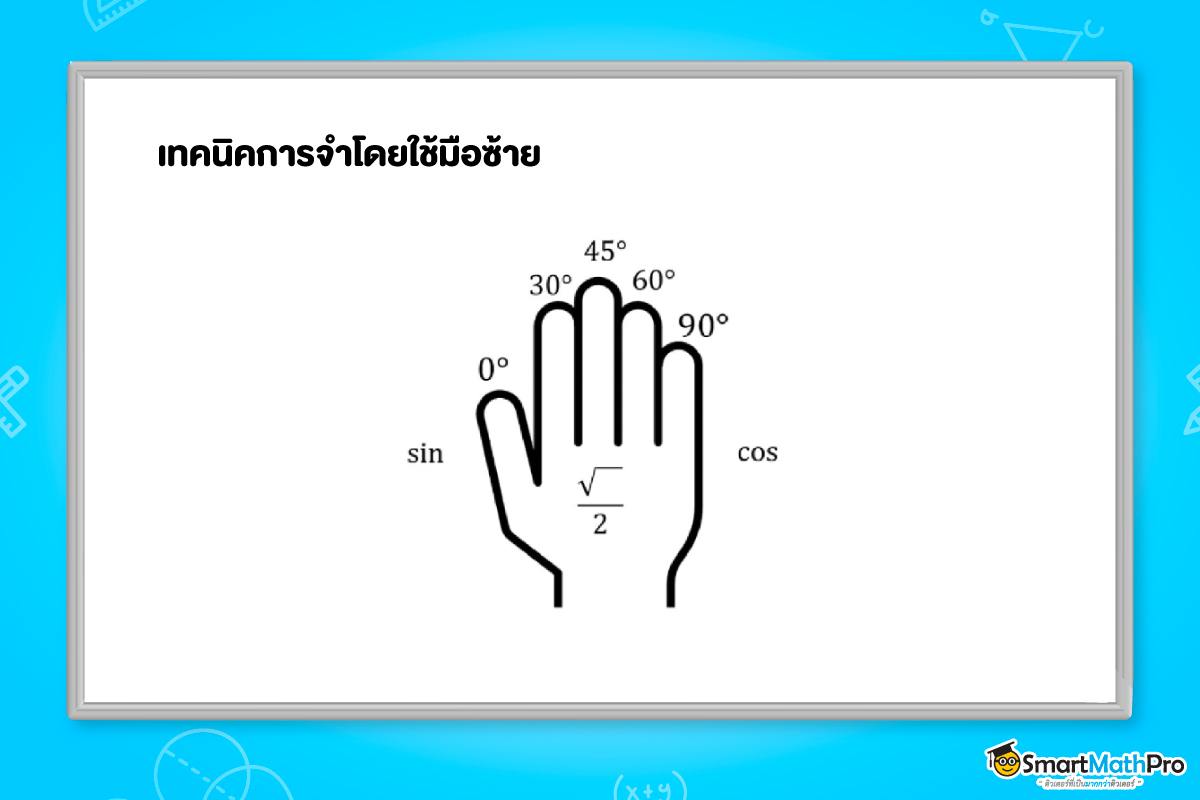
การหา sin30° และ cos45° โดยใช้เทคนิคมือซ้าย
การหาค่า sin30^{\circ}
1. ให้พับนิ้วชี้มือซ้ายลง
2. พิจารณาว่าด้านซ้ายของนิ้วที่พับลงมีนิ้วอยู่กี่นิ้ว (จะได้ว่ามี 1 นิ้ว)
3. นำจำนวนที่ได้มาใส่ใน \sqrt{} (กรณฑ์ที่ 2)
4. จะได้ว่า sin30^{\circ} = \frac{\sqrt{1}}{2} = \frac{1}{2}
การหาค่า cos45^{\circ}
1. ให้พับนิ้วกลางมือซ้ายลง
2. พิจารณาว่าด้านขวาของนิ้วที่พับลงมีนิ้วอยู่กี่นิ้ว (จะได้ว่ามี 2 นิ้ว)
3. นำจำนวนที่ได้มาใส่ใน \sqrt{} (กรณฑ์ที่ 2)
4. จะได้ว่า cos45^{\circ} = \frac{\sqrt{2}}{2}
โคฟังก์ชัน (co-function)
ก่อนจะพูดถึงสูตรเรามาสังเกตจากชื่อเต็มกันก่อน
(sin) sine → (cos) cosine
(tan) tangent → (cot) cotangent
(sec) secant → (cosec) cosecant
จะเห็นว่าชื่อเต็มของ \cos คือ \textrm{cosine} ซึ่งคล้ายกับ \textrm{sine} แต่มีการเติม \textrm{co-} เพิ่มเข้ามา ดังนั้น \sin กับ \cos จึงถือว่าเป็น
“โคฟังก์ชัน” กัน ในทำนองเดียวกัน \tan กับ \cot และ \sec กับ \cosec ก็เป็นโคฟังก์ชันซึ่งกันและกัน
สูตรโคฟังก์ชันเป็นสูตรที่กล่าวถึงมุม A และมุม B ที่มีผลรวมได้ 90^{\circ} แล้วค่า “โคฟังก์ชัน” ของมุม A จะเท่ากันกับมุม B
เช่น sin10^{\circ} = cos80^{\circ}
tan25^{\circ} = cot65^{\circ}
cosec30^{\circ} = sec60^{\circ}
ฟังก์ชันตรีโกณมิติของมุมลบ
เมื่อ \theta>0 (เป็นบวก) จะวัดไปในทิศทางทวนเข็มนาฬิกา
เมื่อ \theta<0 (เป็นลบ) จะวัดไปในทิศทางตามเข็มนาฬิกา ดังรูป
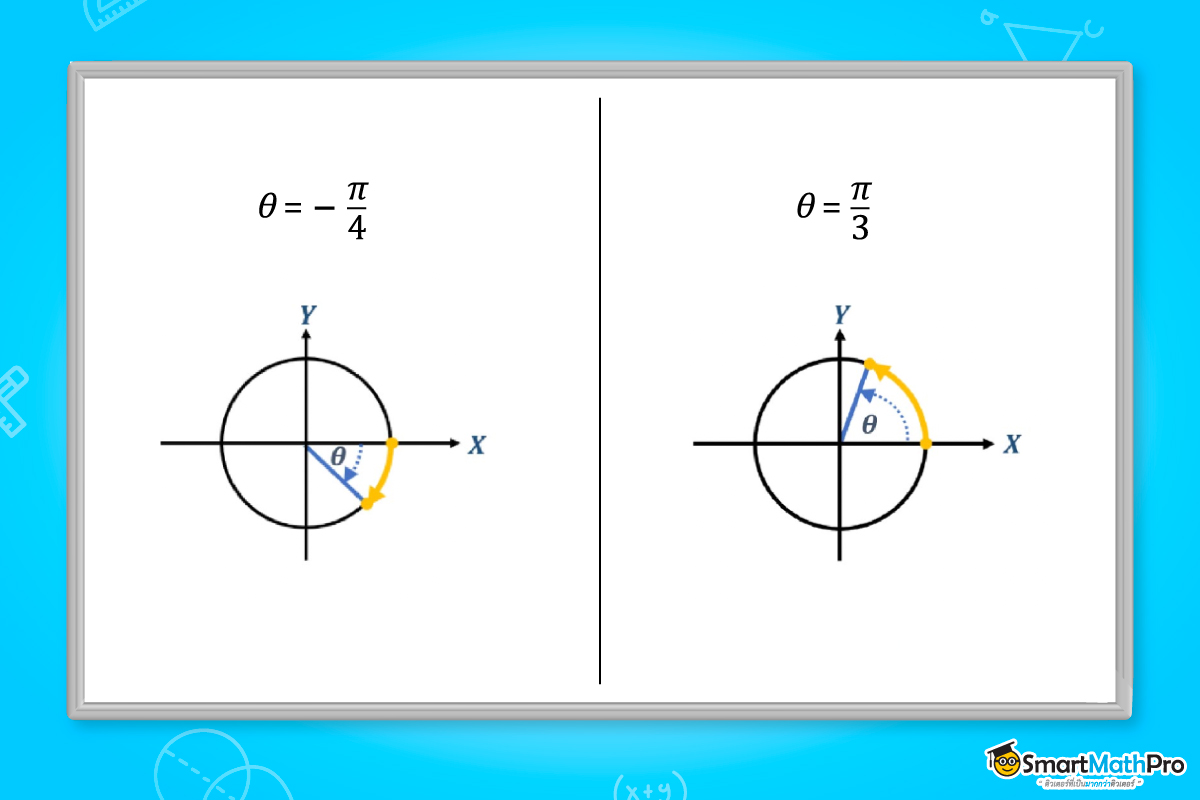
สูตรของฟังก์ชันตรีโกณมิติที่ควรรู้
cos B = \frac{1}{\sqrt{5}}, -\frac{\pi}{2}<B<0 จงหา sin(A+B)
= 1-(-\frac{\sqrt{3}}{2})
= 1+\frac{\sqrt{3}}{2}
= \frac{2+\sqrt{3}}{2}
สูตรแปลงผลบวกเป็นผลคูณ
จะเห็นว่าไม่มีสูตรแปลงผลบวกระหว่าง \sin กับ \cos
ดังนั้นถ้าน้อง ๆ อยากใช้สูตร สามารถใช้โคฟังก์ชันแปลงจาก \sin ให้เป็น \cos หรือจาก \cos เป็น \sin ได้ ดังตัวอย่าง
โคฟังก์ชันในการเปล่ียนก่อน ให้เป็น cosA+cosB ก่อนแล้วจึงใช้สูตร
สูตรมุมสองเท่า
สมการตรีโกณมิติ
การแก้สมการตรีโกณมิติทำได้ในทำนองเดียวกันกับการแก้สมการทั่ว ๆ ไป แต่ต้องใช้ความรู้เกี่ยวกับฟังก์ชันตรีโกณมิติเพื่อหาคำตอบของสมการ
ถ้าโจทย์ไม่กำหนดให้คำตอบต้องอยู่ในช่วงใดช่วงหนึ่ง เราควรตอบคำตอบในรูปทั่วไป เพราะว่าฟังก์ชันตรีโกณมิติไม่เป็นฟังก์ชัน 1-1 ดังนั้นค่าของฟังก์ชันตรีโกณมิติของจำนวนจริงหรือมุมใด ๆ อาจจะซ้ำกันได้นะ
2. ไม่มีเงื่อนไขเพิ่มเติม
คำตอบด้วยนะ
2. คำตอบทั่วไปของสมการ คือ 2n\pi+\frac{\pi }{4} เมื่อ n เป็นจำนวนเต็ม
หมายเหตุ : หลังจากหาคำตอบได้แล้ว เราใช้การบวก 2n\pi เพื่อสร้างคำตอบทั่วไปได้
กราฟของฟังก์ชันตรีโกณมิติ
วิชาฟิสิกส์นำความรู้เรื่องฟังก์ชันตรีโกณมิติมาจำลองรูปแบบคล่ืนต่าง ๆ ที่เกิดขึ้น ซึ่งจะใช้ลักษณะของ
y=sinx, y=cosx, y=tanx ดังนี้
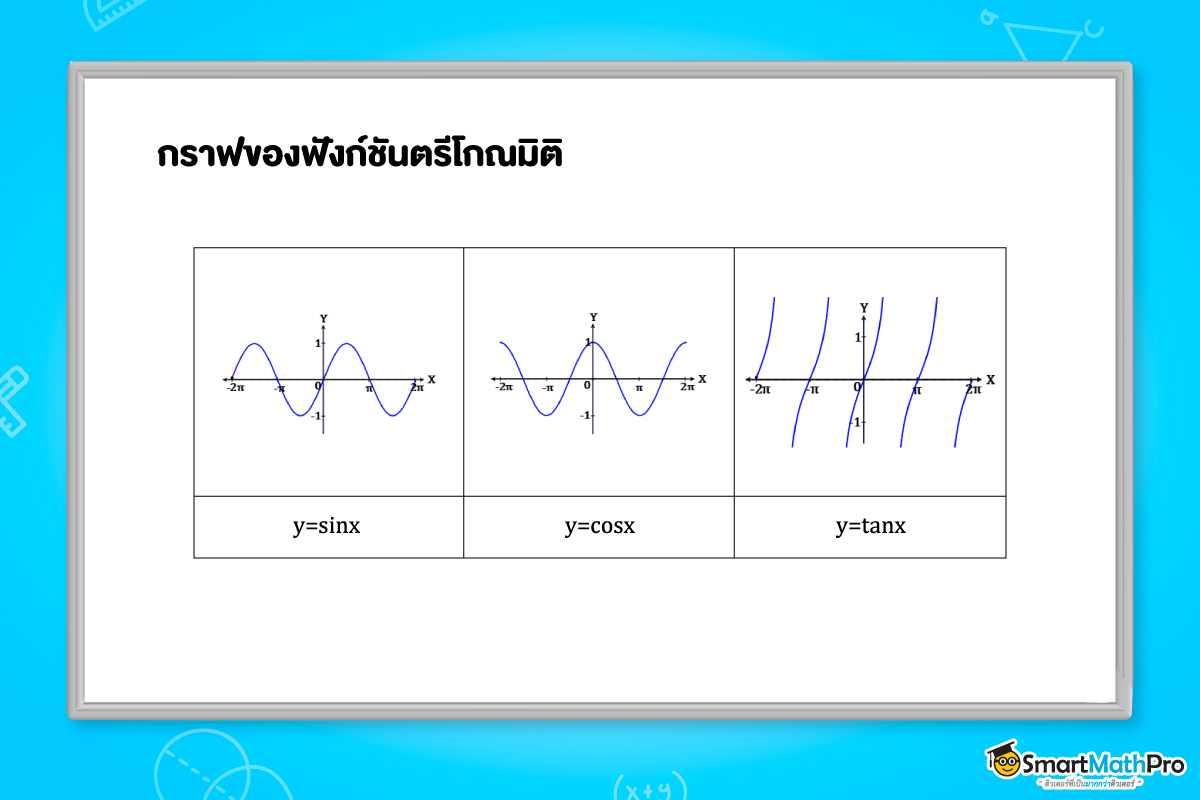
กราฟของฟังก์ชันตรีโกณมิติเป็น ฟังก์ชันที่เป็นคาบ (periodic function) หมายความว่าเราสามารถแบ่งแกน X เป็น
ช่วงย่อย (subinterval) โดยที่ความยาวของแต่ละช่วงย่อยเท่ากัน และกราฟในช่วงย่อยมีลักษณะเหมือนกัน
ความยาวของช่วงย่อยที่สั้นที่สุดเรียกว่า คาบ (period) ของฟังก์ชัน และสำหรับฟังก์ชันที่เป็นคาบซึ่งมีค่าสูงสุดและค่าต่ำสุดของฟังก์ชันนั้นว่า แอมพลิจูด (amplitude)
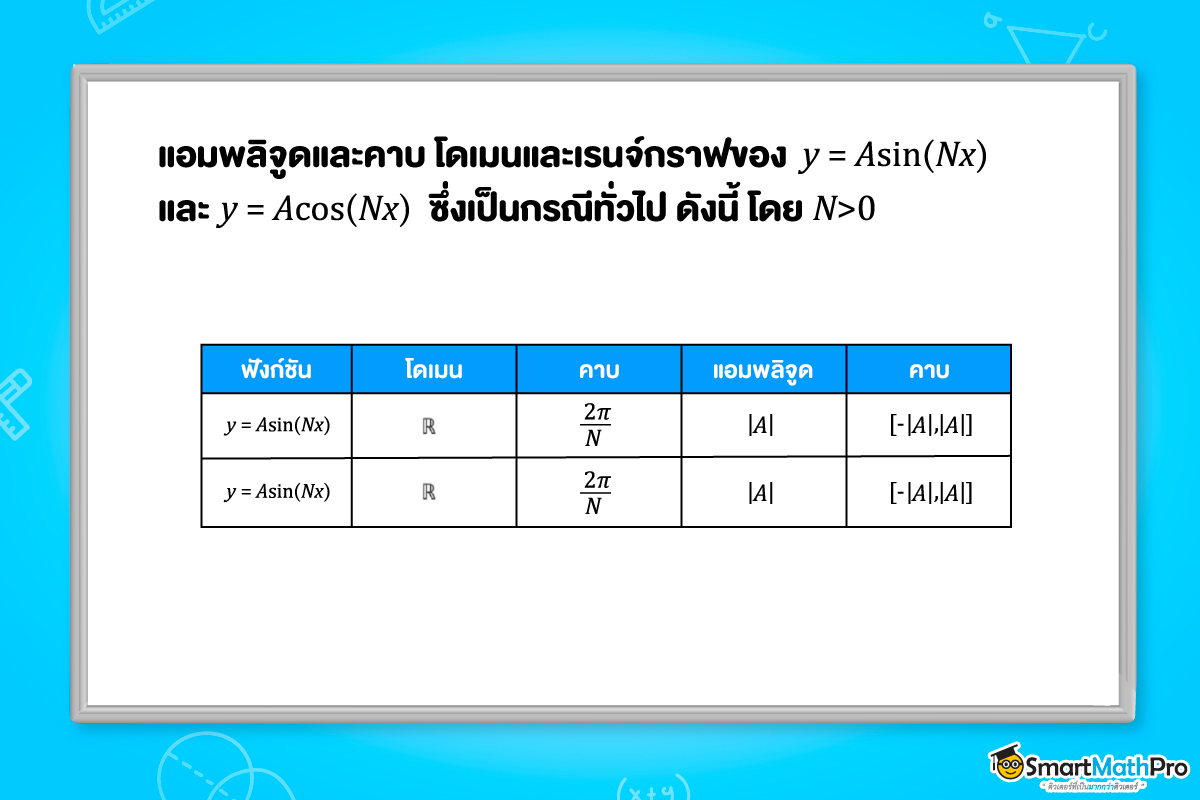
จากคาบ คือ \frac{2\pi}{N}
ดังนั้น \frac{2\pi}{N}=\frac{2\pi}{2}=\pi
จาก แอมพลิจูด คือ |A|
ดังนั้น |A| = |3| = 3
จะได้ว่าโดเมนของฟังก์ชัน คือ ℝ
จาก เรนจ์ คือ [-|A|,|A|]
จะได้ [-|A|,|A|] = [-|3|, |3|] = [-3,3]
ดังนั้น คาบ คือ \pi , แอมพลิจูด คือ 3, โดเมน คือ ℝ และเรนจ์ คือ [-3,3]
ตัวผกผันของฟังก์ชันตรีโกณมิติ
จะขอยกตัวอย่างเนื่องจากที่ผ่านมาเรากล่าวถึง sin30^{\circ} มีค่าเท่ากับ \frac{1}{2} ซึ่งเป็นค่าของฟังก์ชันตรีโกณมิติ ตัวผกผันจะกล่าวถึงมุม เช่น มุมใดที่ทำให้ค่าของ sinA มีค่าเท่ากับ \frac{1}{2}
ฟังก์ชัน \arcsin, \arccos, \arctan จะเป็นตัวผกผันของฟังก์ชัน \sin, \cos, \tan ตามลำดับ
การหาค่าของฟังก์ชันผกผันตรีโกณมิติสามารถทำได้โดยอาศัยฟังก์ชันตรีโกณมิตินั้น ๆ เช่น การหาค่าของฟังก์ชัน \textrm{arcsinx} โดยที่ -1 ≤ x ≤ 1 ก็คือการหา \theta ซึ่งอยู่ในเรนจ์ของฟังก์ชัน \arcsin ที่ทำให้ sin\theta=x
ตัวอย่างเช่น arcsin(1) คือการหา \theta ซึ่ง ที่ทำให้ \sin\theta= 1
สรุปได้ว่าฟังก์ชันตรีโกณมิติที่กำหนดโดเมนเพื่อให้มีฟังก์ชันผกผัน มีโดเมนและเรนจ์ดังนี้
ระวัง ! sin(arsinx) จะเท่ากับ x เมื่อ x อยู่ในเรนจ์ของ sin เท่านั้น
arcsin(sinx) จะเท่ากับ x เมื่อ x อยู่ในเรนจ์ของ arcsin เท่านั้น
เช่น \arcsin \sin120^{\circ}=\arcsin\frac{\sqrt{3}}{2}=60^{\circ} ไม่ใช่ 120^{\circ}
จะได้ sin\theta=-\frac{\sqrt{3}}{2}
จากเรนจ์ เนื่องจากในช่วง [-\frac{\pi}{2},\frac{\pi}{2}] มี -\frac{\pi}{3} เพียงค่าเดียวที่ sin(-\frac{\pi}{3})=-\frac{\sqrt{3}}{2}
ดังนั้น arcsin(-\frac{\sqrt{3}}{2})=-\frac{\pi}{3}
และ cos(arcsin(-\frac{\sqrt{3}}{2}))=cos(\frac{-\pi}{3})=\frac{1}{2}
กฎของโคไซน์และกฎของไซน์
เนื่องจากฟังก์ชันตรีโกณมิติเป็นฟังก์ชันของจำนวนจริงหรือขนาดของมุม โดยเราจะนำความรู้มาหาความยาวด้านและขนาดของมุมในหัวข้อนี้ ซึ่งจะกล่าวถึงความสัมพันธ์ระหว่างด้านและมุมของรูปสามเหล่ียมและฟังก์ชันตรีโกณมิติ
กฎของโคไซน์
ให้รูปสามเหล่ียม ABC มีด้านตรงข้ามมุม A, B, และ C ยาว a, b และ c ตามลำดับ จะได้
a^{2} = b^{2} + c^{2} – 2bccos A
b^{2} = c^{2} + a^{2} – 2cacos B
c^{2} = a^{2} + b^{2} – 2abcos C
กฎของไซน์
ให้รูปสามเหล่ียม ABC มีด้านตรงข้ามมุม A, B และ C ยาว a, b และ c ตามลำดับ จะได้
\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}
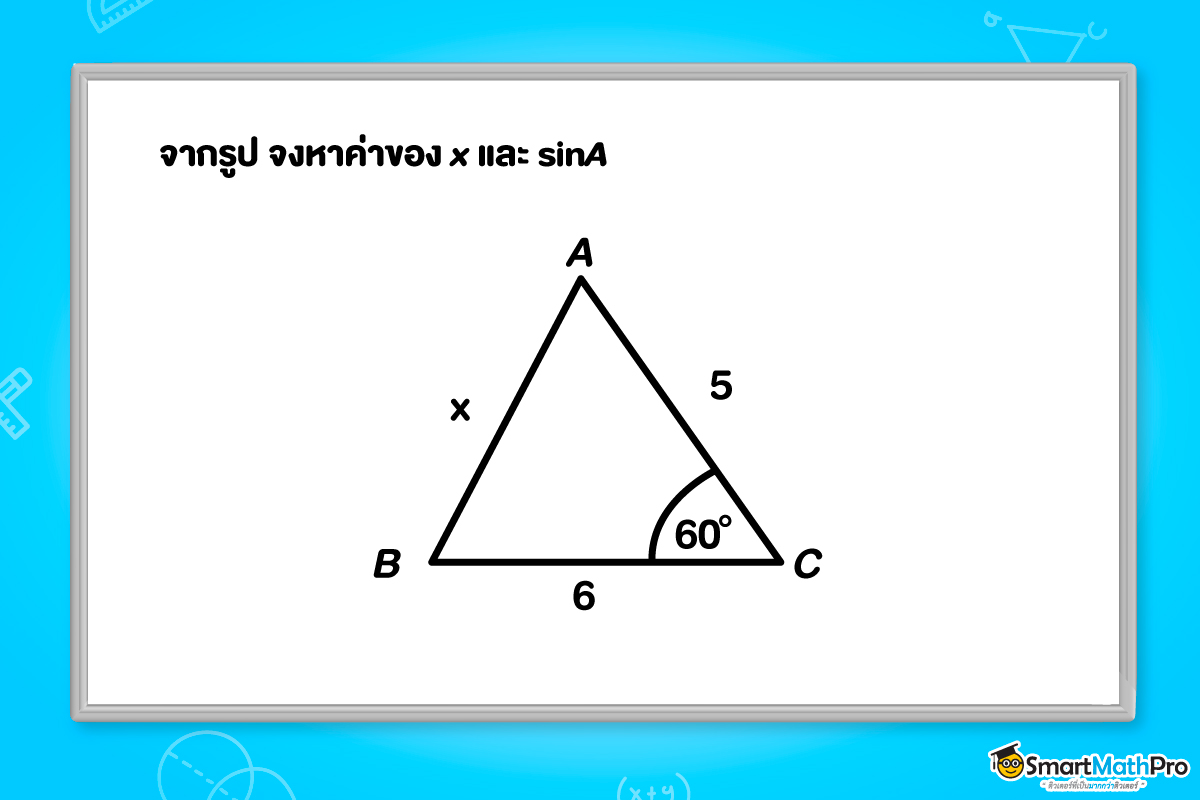
วิธีทำ
1) พิจารณาค่าของ x
จากกฎของโคไซน์ c^2=a^2+b^2-2ab\cos C
จะได้
c^2=a^2+b^2-2ab\cos C
x^2=6^2+5^2-2(6)(5)\cos 60^{\circ}
x^2=36+25-60\left( \frac{1}2{} \right)
x^2=31
x=\sqrt{31}, -\sqrt{31}
เนื่องจาก x เป็นความยาวด้านของรูปสามเหล่ียม
ดังนั้น x=\sqrt{31}
2) พิจารณาค่าของ \sin A
จากกฎของไซน์ \frac{\sin A}{a}=\frac{\sin C}{c}
จะได้
\frac{\sin A}{6}=\frac{\sin 60^{\circ}}{\sqrt{31}}
\sin A =\frac{\frac{\sqrt{3}}{2}}{\sqrt{31}}\times 6
\sin A =\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{31}}\times 6
\sin A=\frac{3\sqrt{3}}{\sqrt{31}}
ดังนั้น \sin A=\frac{3\sqrt{93}}{31}
การหาระยะทางและความสูง
เราสามารถใช้ความรู้เรื่องฟังก์ชันตรีโกณมิติในการหาระยะทางและความสูง ซึ่งมุมที่เกี่ยวข้องจะใช้คำว่ามุมก้มและมุมเงย ซึ่งเกิดจากแนวระดับสายตา และแนวการมองไปยังวัตถุ มุมก้มคือมุมที่เกิดจากการมองวัตถุที่อยู่ต่ำกว่าระดับสายตา และมุมเงย คือ มุมที่เกิดจากการมองวัตถุที่อยู่สูงกว่าระดับสายตา
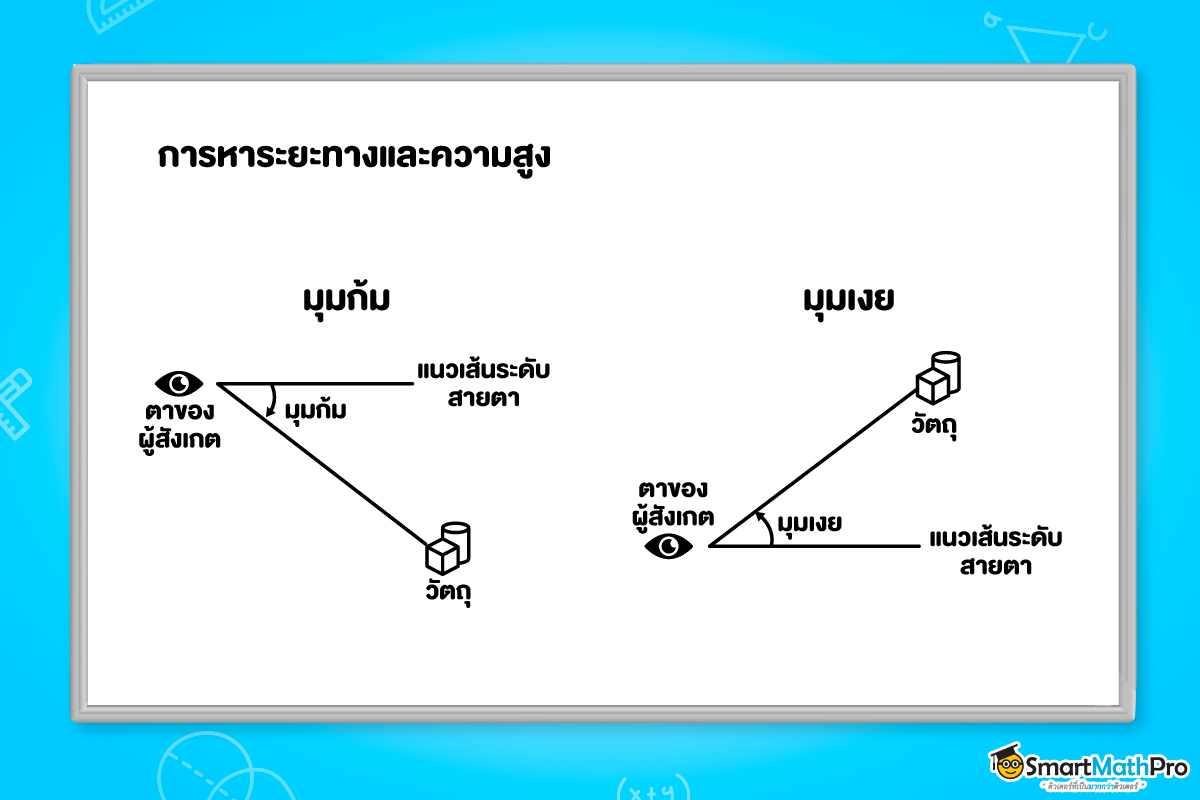
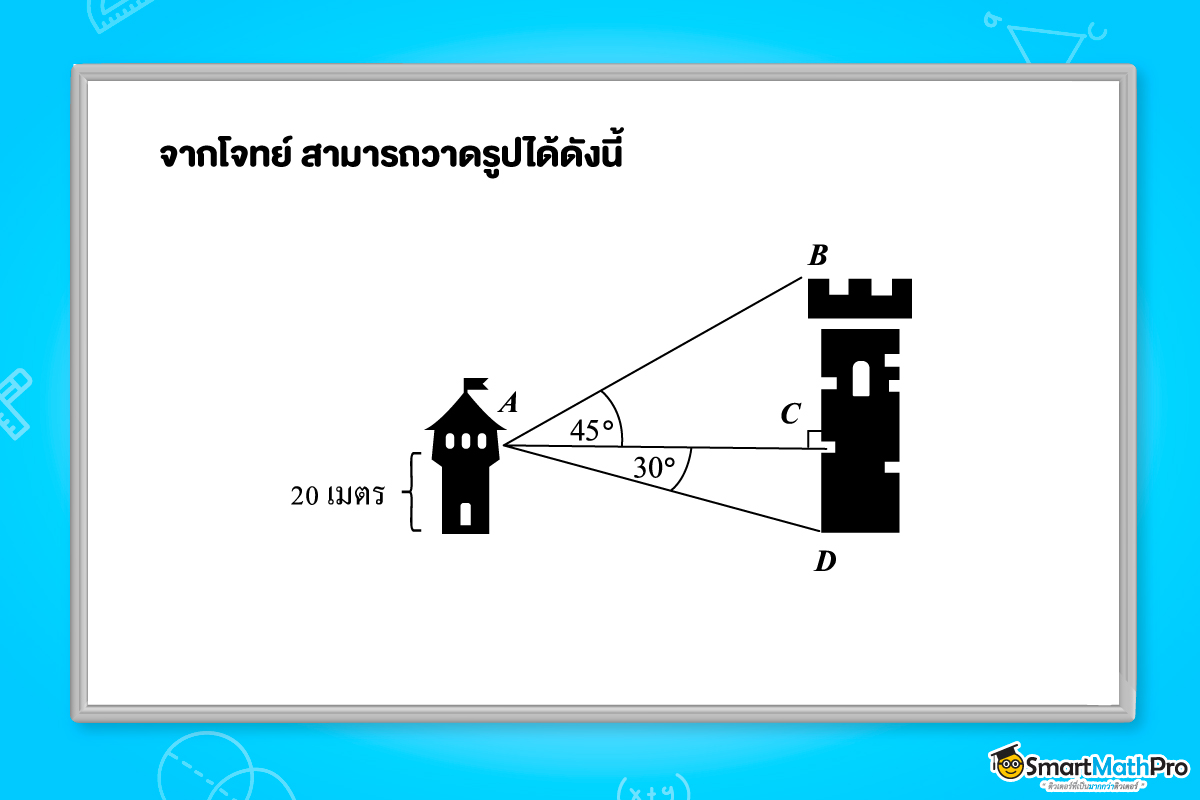
ตัวอย่างที่ 11 ยูตะยืนมองจากหน้าต่างห้องพักในปราสาทไปยังหอคอย เขามองยอดหอคอยเป็นมุมเงย 45^{\circ} และมองฐานหอคอยเป็นมุมก้ม 30^{\circ} ถ้าหน้าต่างห้องพักอยู่สูงจากพื้นดิน 20^{\circ} เมตร แล้วหอคอยสูงกี่เมตร
แนวคิด จากโจทย์สามารถวาดภาพประกอบได้ดังนี้ ซึ่งโจทย์ต้องการหาส่วนสูงของหอคอย ดังนั้นต้องหา BC แล้วนำมาบวกกันกับ CD
2. พิจารณารูปสามเหล่ียม ABC
จะได้ tan45=\frac{BC}{AC}
1=\frac{BC}{20\sqrt{3}}
BC=20\sqrt{3}
ดังนั้นส่วนสูงของหอคอยเท่ากับ
BC+DC = 20\sqrt{3}+20 เมตร
เป็นยังไงกันบ้างกับ “ฟังก์ชันตรีโกณมิติ” ที่เพิ่งอ่านจบกันไป ถ้าใครอ่านสรุปเนื้อหาแล้วยังรู้สึกไม่เข้าใจ ก็ไม่เป็นไรน้าา เพราะเนื้อหาฟังก์ชันตรีโกณมิติ ม.5 เนี่ยขึ้นชื่อว่าหินสุด ๆ แต่พี่เชื่อว่าถ้าเรามีพื้นฐานที่ดี ทบทวนบทเรียนและฝึกทำโจทย์บ่อย ๆ ก็จะทำให้เข้าใจในเนื้อหามากขึ้น ซึ่งถ้าใครอยากได้แบบฝึกหัดไปซ้อมมือ พี่มี แบบฝึกหัดตรีโกณมิติ ม.5 ที่รวบรวมโจทย์ไว้เยอะมากก
แต่ถ้าใครยังกังวล กลัวว่าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์ พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เพราะแพ็ก ม.5 – ม.6 เรียนได้ถึง 2 ปี และแพ็ก ม.4 – ม.6 เรียนได้ถึง 3 ปี พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากกกก นอกจากนี้ยังพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ และถ้าแพ็กไม่ตรงกับที่โรงเรียนสอน น้อง ๆ ก็สามารถเลือกเป็นคอร์สแยกบทได้ เพราะมีคอร์สติวแยกบทของคณิต ม.ปลาย ทุกบทเลย แน่นอนว่ามีส่วนลดพิเศษเช่นกันน้า ใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ไปดูรายละเอียดได้เลยยย
ดูคลิปติวฟังก์ชันตรีโกณมิติ ม.5
ดูคลิปอื่น ๆ เพิ่มเติมได้ที่ YouTube : SmartMathPro
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
คณิตศาสตร์ ม.5 เทอม 1 และเทอม 2 เรียนอะไรบ้าง ? สรุปครบทั้งคณิตพื้นฐานและเพิ่มเติม
จำนวนเชิงซ้อน ม.5 คืออะไร ? สรุปเนื้อหา พร้อมตัวอย่างโจทย์
เวกเตอร์ ม.5 สรุปทุกเนื้อหา พร้อมโจทย์และวิธีทำที่ทุกคนห้ามพลาด!
เมทริกซ์ ม.5 สรุปเนื้อหาครบทุกหัวข้อ !!
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
