สรุป ความน่าจะเป็น ม.3 พร้อมแจกโจทย์และเฉลยฟรี!!

เมื่อพูดถึง “ความน่าจะเป็น” ทุกคนเคยสังเกตกันไหมว่า มีความน่าจะเป็นที่ซ่อนอยู่ในชีวิตประจำวันของเราเยอะเลยน้าา เช่น ความน่าจะเป็นที่เราจะจับฉลากได้รางวัลใหญ่ หรือความน่าจะเป็นที่คุณครูจะออกข้อสอบตรงกับที่เราอ่านมา
มากแค่ไหน ซึ่งเหตุการณ์เหล่านี้ก็เกี่ยวกับเนื้อหาคณิตศาสตร์ด้วย ก็คือเรื่อง ความน่าจะเป็น นั่นเองง

เพื่อให้เข้าใจเกี่ยวกับความน่าจะเป็นรอบตัวเรามากขึ้น พี่ก็เลยจะพาทุกคนมารู้จักกับความน่าจะเป็นในรูปแบบต่าง ๆ ของเนื้อหาคณิตศาสตร์ เรื่อง ความน่าจะเป็น ม.3 พร้อมวิธีการคำนวณ รวมถึงการใช้ตารางและแผนภูมิต้นไม้มาช่วยหา
ความน่าจะเป็นด้วย ถ้าทุกคนพร้อมแล้ว ก็ไปลุยกันนน

สนใจหัวข้อไหน ... กดอ่านเลย

โอกาสของเหตุการณ์

ในชีวิตประจำวัน เราอาจจะเคยพบคำว่า “มีโอกาสที่” “คาดการณ์ว่า” “มีเกณฑ์ว่า” หรือ “เป็นไปได้ว่า” โดยคำเหล่านี้เป็นคำสำคัญที่แสดงให้เห็นถึงโอกาสที่เหตุการณ์หนึ่ง ๆ จะเกิดขึ้น เช่น จากการรายงานข่าว หรือการสรุปเหตุการณ์ต่าง ๆ ผ่านสื่อสังคมออนไลน์ ซึ่งโอกาสหรือแนวโน้มที่เหตุการณ์เหล่านั้นจะเกิดขึ้น เราจะเรียกว่า โอกาสของเหตุการณ์ (chance of event)

โดยโอกาสที่เหตุการณ์หนึ่ง ๆ จะเกิดขึ้นนั้นอาจเกิดขึ้นอย่างแน่นอน หรือ อาจจะเกิดขึ้นหรือไม่ก็ได้ หรือ ไม่เกิดขึ้น
อย่างแน่นอน อย่างใดอย่างหนึ่งเพียงอย่างเดียวเท่านั้น เพื่อให้เข้าใจได้มากขึ้น เราลองไปดูตัวอย่างนี้กันน

ตัวอย่างที่ 1 ทอดลูกเต๋า 1 ลูก 1 ครั้ง จงพิจารณาโอกาสของเหตุการณ์ต่อไปนี้ว่า เกิดขึ้นอย่างแน่นอน อาจจะเกิดขึ้นหรือไม่ก็ได้ หรือไม่เกิดขึ้นอย่างแน่นอน

1. โอกาสที่ลูกเต๋าจะขึ้นแต้ม 0
ตอบ ไม่เกิดขึ้นอย่างแน่นอน เพราะลูกเต๋าไม่มีแต้ม 0 จึงไม่มีโอกาสที่ลูกเต๋าจะขึ้นแต้ม 0

2. โอกาสที่ลูกเต๋าจะขึ้นแต้ม 4
ตอบ อาจจะเกิดขึ้นหรือไม่ก็ได้ เพราะมีโอกาสที่ลูกเต๋าจะขึ้นแต้ม 4 หรือ 1, 2, 3, 5 หรือ 6 ก็ได้

3. โอกาสที่ลูกเต๋าจะขึ้นแต้มใดแต้มหนึ่ง จากแต้ม 1 ถึง 6
ตอบ เกิดขึ้นอย่างแน่นอน เพราะลูกเต๋ามีแต้มตั้งแต่ 1 ถึง 6

การทดลองสุ่ม

การทดลองสุ่ม (random experiment) คือ สถานการณ์ที่ไม่สามารถบอกล่วงหน้าได้แน่นอน ว่าผลลัพธ์ของ
การกระทำจะเป็นอะไร แต่สามารถบอกได้ว่ามีผลลัพธ์อะไรเกิดขึ้นได้บ้าง

ตัวอย่างที่ 2 จงพิจารณาสถานการณ์ต่อไปนี้ว่าเป็นการทดลองสุ่มหรือไม่

1. การออกรางวัลสลากกินแบ่งรัฐบาล
ตอบ เป็นการทดลองสุ่ม

2. ผลการแข่งขันฟุตบอลพรีเมียร์ลีก
ตอบ ไม่เป็นการทดลองสุ่ม

3. เนยทำข้อสอบชุดหนึ่งจนเสร็จครบทุกข้อ
ตอบ ไม่เป็นการทดลองสุ่ม

การหาจำนวนผลลัพธ์ของการทดลองสุ่ม

หลังจากที่น้อง ๆ พอจะรู้จักกับความหมายของการทดลองสุ่ม และตัวอย่างสถานการณ์ที่เป็นการทดลองสุ่มแล้ว
ในหัวข้อนี้เราจะมาเรียนรู้เกี่ยวกับผลลัพธ์ และจำนวนผลลัพธ์ของการทดลองสุ่มกัน

ผลลัพธ์จากการทดลองสุ่ม หมายถึง ผลลัพธ์ที่มีโอกาสที่จะเกิดขึ้นเท่า ๆ กัน

ตัวอย่างที่ 3 จงหาผลลัพธ์จากการทดลองสุ่ม และจำนวนผลลัพธ์ของการทดลองสุ่มต่อไปนี้

1. ทอดลูกเต๋า 1 ลูก 1 ครั้ง

ผลลัพธ์จากการทดลองสุ่ม คือ 1, 2, 3, 4, 5 และ 6
จำนวนผลลัพธ์ของการทดลองสุ่ม คือ 6

2. สุ่มหยิบลูกบอล 2 ลูก จากกล่องใบหนึ่ง ที่มีลูกบอลสีขาว สีแดง และสีฟ้าอย่างละ 1 ลูก โดยหยิบทีละลูกแบบไม่ใส่คืนก่อนหยิบครั้งถัดไป

ผลลัพธ์จากการทดลองสุ่ม คือ (ขาว, แดง), (แดง, ขาว), (ขาว, ฟ้า), (ฟ้า, ขาว), (แดง, ฟ้า) และ (ฟ้า, แดง)
จำนวนผลลัพธ์ของการทดลองสุ่ม คือ 6

3. สุ่มหยิบลูกบอล 2 ลูกพร้อมกัน จากกล่องใบหนึ่ง ที่มีลูกบอลสีขาว สีแดง และสีฟ้าอย่างละ 1 ลูก

ผลลัพธ์จากการทดลองสุ่ม คือ (ขาว, แดง), (ขาว, ฟ้า) และ (แดง, ฟ้า)
จำนวนผลลัพธ์ของการทดลองสุ่ม คือ 3

เหตุการณ์

จากเรื่องการทดลองสุ่มที่ทุกคนเพิ่งอ่านไป น้อง ๆ คงได้เห็นตัวอย่างการหาจำนวนผลลัพธ์ทั้งหมดจากการทดลองสุ่ม
ไปแล้ว ซึ่งถ้าเราสนใจผลลัพธ์แค่บางผลลัพธ์จากการทดลองสุ่ม เราจะเรียกผลลัพธ์นี้ว่า เหตุการณ์ น้าา

เหตุการณ์ (event) คือ ผลลัพธ์ของการทดลองสุ่มที่สนใจ โดยกำหนดเงื่อนไขเพิ่มเติมบางประการ
ผลลัพธ์ของเหตุการณ์ หมายถึง ผลลัพธ์ทั้งหมดของสิ่งที่สนใจที่เกิดขึ้นจากการทดลองสุ่ม

การหาจำนวนผลลัพธ์ของเหตุการณ์

ในการหาจำนวนผลลัพธ์ของเหตุการณ์ จะคล้ายกับการหาผลลัพธ์ของการทดลองสุ่ม แต่เราจะนับแค่ผลลัพธ์
ที่เราสนใจเท่านั้น

ตัวอย่างที่ 4 ทอดลูกเต๋า 2 ลูก ที่สีต่างกัน จงหาผลลัพธ์ของเหตุการณ์ที่ผลรวมของลูกเต๋าทั้งสองเท่ากับ 6

แนวคิด จำนวน 1 – 6 ที่บวกกันแล้วได้ 6 คือ 1+5, 2+4, 3+3

วิธีทำ เหตุการณ์ที่ผลรวมของลูกเต๋าทั้งสองเท่ากับ 6
ลูกเต๋าสีที่หนึ่งออกแต้ม 1 และลูกเต๋าสีที่สองออกแต้ม 5
ลูกเต๋าสีที่หนึ่งออกแต้ม 2 และลูกเต๋าสีที่สองออกแต้ม 4
ลูกเต๋าสีที่หนึ่งออกแต้ม 3 และลูกเต๋าสีที่สองออกแต้ม 3
ลูกเต๋าสีที่หนึ่งออกแต้ม 4 และลูกเต๋าสีที่สองออกแต้ม 2
ลูกเต๋าสีที่หนึ่งออกแต้ม 5 และลูกเต๋าสีที่สองออกแต้ม 1

ดังนั้น ผลลัพธ์ของเหตุการณ์นี้มีทั้งหมด 5 แบบคือ (1, 5), (2, 4), (3, 3), (4, 2), (5, 1)

ตัวอย่างที่ 5 จากการโยนเหรียญ 2 เหรียญที่แตกต่างกัน 1 ครั้ง จงหาผลลัพธ์ของเหตุการณ์ที่เหรียญออกก้อยอย่างน้อย 1 ครั้ง

แนวคิด ในการโยนเหรียญแล้วออกก้อยอย่างน้อยหนึ่งเหรียญ แสดงว่าเราสนใจเหตุการณ์ที่เหรียญออกก้อย 1 เหรียญ และเหตุการณ์ที่เหรียญออกก้อย 2 เหรียญ

วิธีทำ ให้ H แทนผลลัพธ์ที่เหรียญออกหัว และ T แทนผลลัพธ์ที่เหรียญออกก้อย

ผลลัพธ์ของการทดลองสุ่มทั้งหมดเป็นดังนี้

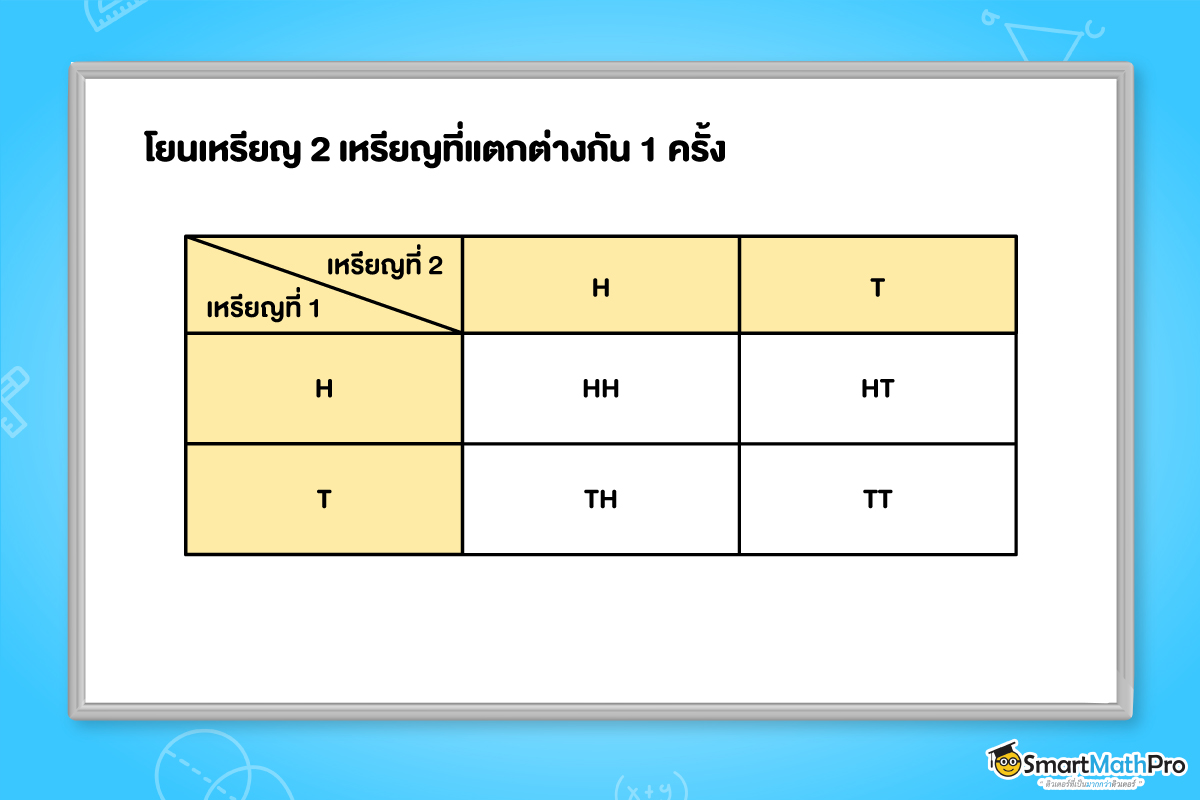
จะได้ว่า ผลลัพธ์ของเหตุการณ์ที่เหรียญออกก้อย 1 ครั้ง คือ HT, TH และผลลัพธ์ของเหตุการณ์ที่เหรียญออกก้อย 2 ครั้ง คือ TT

ดังนั้น ผลลัพธ์ของเหตุการณ์ที่เหรียญออกก้อยอย่างน้อย 1 ครั้งคือ HT, TH, TT

หมายเหตุ : น้อง ๆ จะเห็นว่าผลลัพธ์ของเหตุการณ์ที่เหรียญไม่ได้ออกก้อยเลยคือ HH ซึ่งเป็นผลลัพธ์เดียวที่เราไม่ได้สนใจ แสดงว่าถ้าเรานำผลลัพธ์ของเหตุการณ์ที่ไม่ได้สนใจลบออกจากผลลัพธ์ของการทดลองสุ่มทั้งหมด เราก็จะได้ผลลัพธ์ของเหตุการณ์ที่เราสนใจเช่นกัน

ตัวอย่างที่ 6 สุ่มหยิบลูกบอล 3 ลูก จากถุงที่บรรจุลูกบอล 3 สี สีละ 1 ลูก ได้แก่ สีเหลือง สีน้ำเงิน และสีฟ้า โดยหยิบลูกบอลทีละลูกแล้วใส่ก่อนที่จะหยิบลูกถัดไป จงหาผลลัพธ์ของเหตุการณ์ที่จะหยิบลูกบอลได้สีต่างกัน

วิธีทำ ให้ ล แทน ผลลัพธ์ที่หยิบได้ลูกบอลสีเหลือง
น แทน ผลลัพธ์ที่หยิบได้ลูกบอลสีน้ำเงิน
ฟ แทน ผลลัพธ์ที่หยิบได้ลูกบอลสีฟ้า

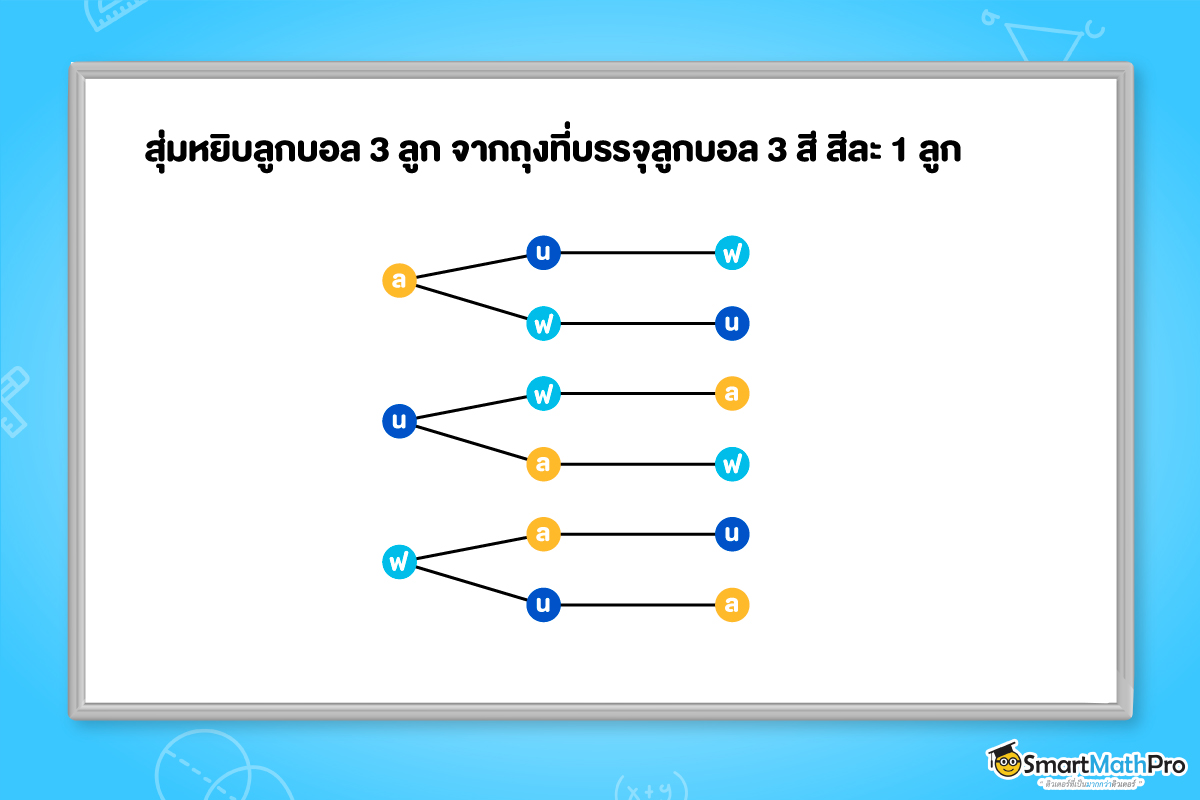
ดังนั้น เหตุการณ์ที่หยิบลูกบอลได้สีต่างกัน คือ (ล, น, ฟ), (ล, ฟ, น), (น, ฟ, ล), (น, ล, ฟ), (ฟ, ล, น), (ฟ, น, ล)

จากตัวอย่างที่ผ่านมา น้องๆ จะเห็นว่าเราสามารถใช้ตารางและแผนภาพต้นไม้มาช่วยในการนับผลลัพธ์ของเหตุการณ์ รวมถึงสามารถใช้ตารางและแผนภาพต้นไม้ในการนับผลลัพธ์ของการทดลองสุ่มได้ด้วย

ความน่าจะเป็น

ความน่าจะเป็นของเหตุการณ์จะเกี่ยวข้องกับจำนวนผลลัพธ์ของเหตุการณ์และจำนวนผลลัพธ์ทั้งหมดที่เกิดขึ้นจาก
การทดลองสุ่มที่น้อง ๆ ได้รู้จักมาแล้วนั่นเองง ซึ่งเราสามารถหาความน่าจะเป็นของเหตุการณ์ใด ๆ จากการทดลองสุ่ม
ได้จากสูตรนี้เลยย

ตัวอย่างที่ 7 สุ่มหยิบลูกบอล 2 ลูก โดยหยิบทีละลูกแบบไม่ใส่คืน จากกล่องใบหนึ่งที่มีลูกบอลสีแดง 2 ลูก และสีขาว 1 ลูก จงหาความน่าจะเป็นของเหตุการณ์ที่หยิบได้ลูกบอลสีเดียวกัน

วิธีทำ ให้ ด1 แทน ลูกบอลสีแดงลูกที่ 1
ด2 แทน ลูกบอลสีแดงลูกที่ 2
ข แทน ลูกบอลสีขาว

ผลลัพธ์ทั้งหมดที่เกิดขึ้นจากการสุ่มหยิบลูกบอล 2 ลูก โดยหยิบทีละลูกแบบไม่ใส่คืน คือ (ด1, ด2), (ด1, ข), (ด2, ด1), (ด2, ข), (ข, ด1), (ข, ด2)

จะได้ จำนวนผลลัพธ์ทั้งหมดที่เกิดขึ้น เท่ากับ 6

ผลลัพธ์ของเหตุการณ์ที่หยิบได้ลูกบอลสีเดียวกัน คือ (ด1, ด2), (ด2, ด1)

จะได้ จำนวนผลลัพธ์ของเหตุการณ์ เท่ากับ 2

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่หยิบได้ลูกบอลสีเดียวกัน คือ $\frac{2}{6}=\frac{1}{3}$

ก็จบกันไปแล้วน้าา กับเนื้อหาความน่าจะเป็น ม.3 ที่พี่สรุปมาให้ทุกคนในวันนี้ เห็นไหมว่าในหลาย ๆ ตัวอย่างที่พี่ยกมา
ก็เกี่ยวข้องกับชีวิตประจำวันของเราที่ทุกคนสามารถเชื่อมโยงเนื้อหาในบทความนี้แล้วเอาไปต่อยอดได้อีกเพียบบ

ซึ่งนอกจากจะเอาไปใช้ได้จริงแล้ว ถ้าใครอยากเข้าใจเนื้อหาบทนี้มากขึ้น พี่ก็แนะนำให้ทบทวนและฝึกทำโจทย์บ่อย ๆ น้าา รับรองว่าน้อง ๆ จะเก่งขึ้นแน่นอน !! (แอบกระซิบว่า พี่มีแบบฝึกหัดให้ทุกคนได้ลองฝึกทำด้วย ไปดาวน์โหลดกันได้เลยย >> แจกฟรี แบบฝึกหัดความน่าจะเป็น ม.3)

ติวคณิตศาสตร์ ม.3 กับ SmartMathPro

สำหรับน้อง ๆ ม.3 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์

พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.3 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก