สรุปตารางค่าความจริง (ตรรกศาสตร์) พร้อมโจทย์และเฉลย

หน้าแรก
เนื้อหาวิชาการ
คณิต ม.ปลาย
สรุปตารางค่าความจริง (ตรรกศาสตร์) พร้อมโจทย์และเฉลย

28 มกราคม 2026
สรุปเนื้อหาคณิต ม.ปลาย

บทความนี้จะพาน้อง ๆ ไปรู้จักกับ การสร้างตารางค่าความจริง ตั้งแต่พื้นฐานการเชื่อมประพจน์ วิธีการสร้างตาราง ไปจนถึงการหาค่าความจริงของประพจน์ในแต่ละกรณี เมื่ออ่านจบแล้ว น้อง ๆ จะสามารถสร้างตารางค่าความจริงได้ครบทุกกรณี ซึ่งจะช่วยปูพื้นฐานให้การเรียนเรื่องตรรกศาสตร์ในบทต่อ ๆ ไปเข้าใจง่ายขึ้นแน่นอน

สนใจหัวข้อไหน ... กดอ่านเลย

การเชื่อมประพจน์

ในชีวิตประจำวันน้อง ๆ จะพบประโยคที่ได้จากการเชื่อมกันมากกว่าหนึ่งประโยค โดยในบทนี้ตัวเชื่อมที่น้อง ๆ จะเจอ ได้แก่ “และ” “หรือ” “ถ้า…แล้ว…” “ก็ต่อเมื่อ” หรือพบประโยคซึ่งเปลี่ยนแปลงมาจากประโยคเดิม โดยเติมคำว่า “ไม่” เข้าไป ซึ่งคำทั้งหมดนี้เราจะเรียกว่า ตัวเชื่อม (connective) ทั้งหมดเลย

ตัวอย่างประโยคที่มีตัวเชื่อม

$2$ ไม่เป็นจำนวนเต็มลบ
$9$ เท่ากับ $10$ หรือ $10$ ไม่น้อยกว่า $9$
ถ้า $5$ เป็นจำนวนตรรกยะ แล้ว $\pi$ เป็นจำนวนอตรรกยะ

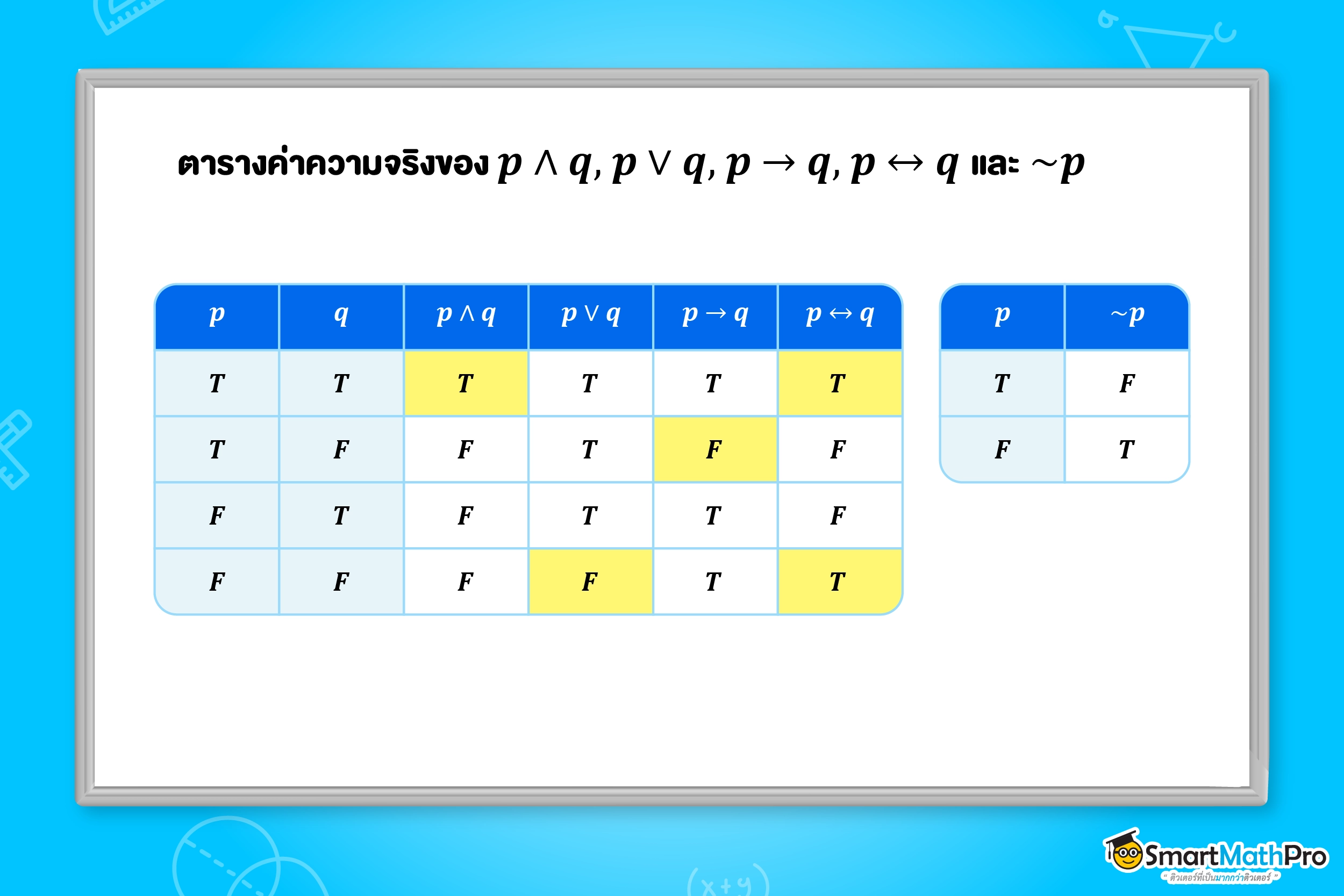
ถ้า $p$ และ $q$ เป็นประพจน์ใด ๆ แล้วการเชื่อมประพจน์ด้วยตัวเชื่อม “และ” “หรือ” “ถ้า…แล้ว…” “ก็ต่อเมื่อ” “ไม่” จะมีการใช้สัญลักษณ์

$p$ และ $q$ เขียนแทนด้วย $p\wedge q$
$p$ หรือ $q$ เขียนแทนด้วย $p\vee q$
ถ้า $p$ แล้ว $q$ เขียนแทนด้วย $p\to q$
$p$ ก็ต่อเมื่อ $q$ เขียนแทนด้วย $p\leftrightarrow q$
นิเสธของ $p$ เขียนแทนด้วย $\sim p$

และจะมีค่าความจริงดังนี้

การสร้างตารางค่าความจริง

หลังจากที่น้อง ๆ รู้จักตารางค่าความจริงของตัวเชื่อมต่าง ๆ แล้ว เรามาดูวิธีการสร้างตารางความจริงกัน โดยตารางค่าความจริงเป็นตารางที่ใช้แสดงผลลัพธ์ค่าความจริงของประพจน์ที่เป็นไปได้ทุกกรณีเพื่อให้เห็นชัดเจนว่าเงื่อนไขใดทำให้ประพจน์รวมเป็นจริงหรือเท็จ

พิจารณาประพจน์ที่มีตัวเชื่อม เช่น $\left( p\vee q \right)\to p$ จะเห็นว่าประพจน์นี้มี $p$ และ $q$ เป็นประพจน์ย่อย
ซึ่งยังไม่กำหนดค่าความจริง จะเรียก $p$ และ $q$ ว่าเป็นตัวแปรแทนประพจน์ใด ๆ และเรียกประพจน์ที่มีตัวเชื่อมนี้ว่า

รูปแบบของประพจน์ (propositional formula)

ถ้า “รูปแบบของประพจน์” มีจำนวน “ประพจน์ย่อย” อยู่ $n$ ประพจน์
แล้วจะมี “กรณีเกี่ยวกับค่าความจริงที่ต้องพิจารณา” ทั้งหมด $2^{n}$ กรณี

การหาค่าความจริงของรูปแบบของประพจน์จะใช้การกำหนดค่าความจริงของประพจน์ย่อยให้ครบทุกกรณีที่เป็นไปได้ เช่น

ถ้ามีประพจน์เดียว คือ $p$ แล้วจะมีกรณีเกี่ยวกับค่าความจริงที่ต้องพิจารณา $2^{1}=2$ กรณี
ถ้ามี $2$ ประพจน์ คือ $p$ และ $q$ แล้วจะมีกรณีเกี่ยวกับค่าความจริงที่ต้องพิจารณา $2^{2}=4$ กรณี
ถ้ามี $3$ ประพจน์ คือ $p,\ q$ และ $r$ แล้วจะมีกรณีเกี่ยวกับค่าความจริงที่ต้องพิจารณา $2^{3}=8$ กรณี

ตัวอย่างที่ 1 กำหนดให้ $p$ และ $q$ เป็นประพจน์ จงสร้างตารางค่าความจริงของ

$\left( p\to q \right)\wedge \sim p$

วิธีทำ

จากโจทย์มี $2$ ประพจน์ย่อย คือ $p$ และ $q$ ดังนั้นจะมีกรณีเกี่ยวกับค่าความจริงทั้งหมด $2^{n}=2^{2}=4$ กรณี

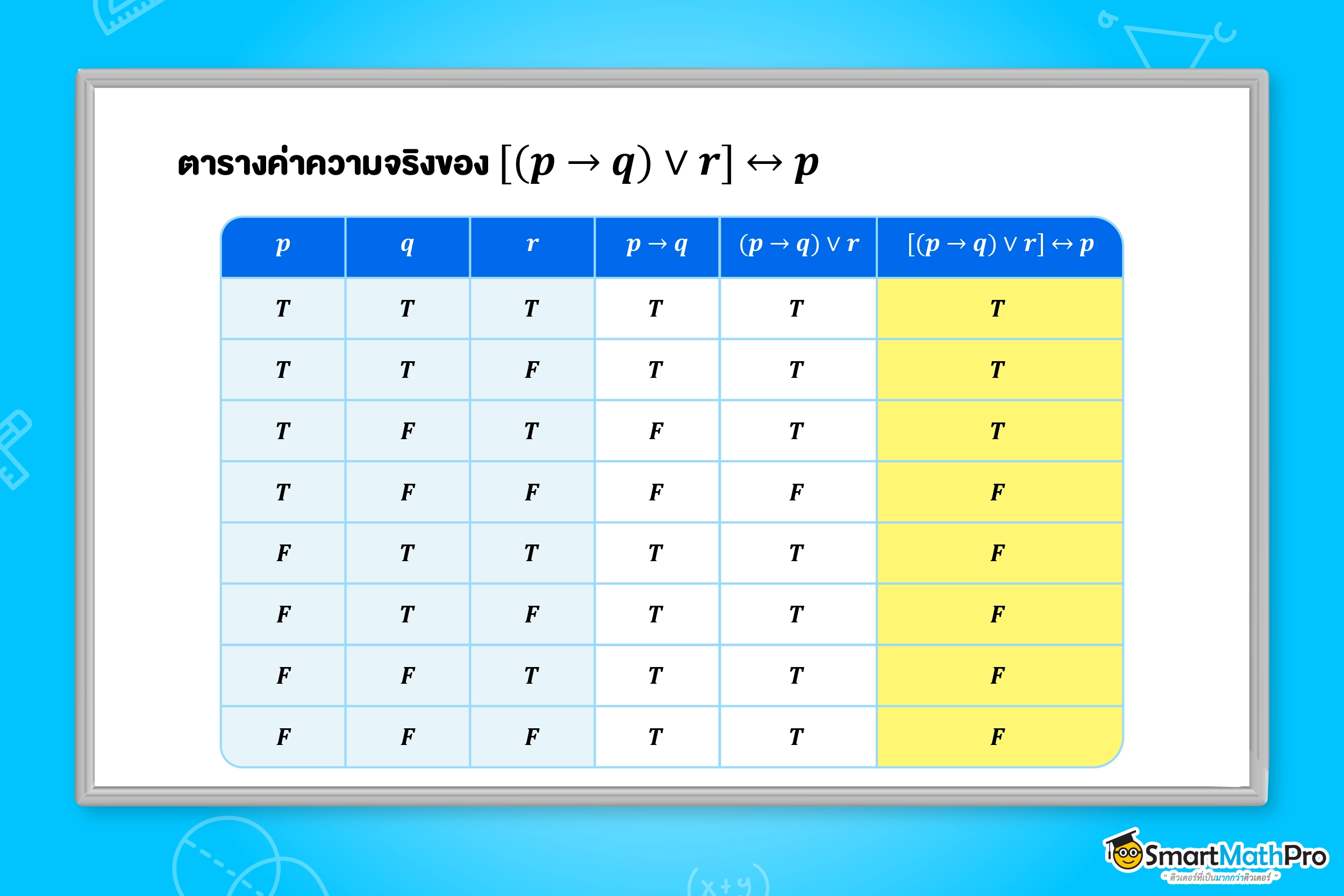
ตัวอย่างที่ 2 กำหนดให้ $p, q$ และ $r$ เป็นประพจน์ จงสร้างตารางค่าความจริงของ $[\left(p\rightarrow q\right)\vee r]\leftrightarrow p$

วิธีทำ

จากโจทย์มี $3$ ประพจน์ย่อย คือ $p,q$ และ $r$ ดังนั้นจะมีกรณีเกี่ยวกับค่าความจริงทั้งหมด $2^{n}=2^{3}=8$ กรณี

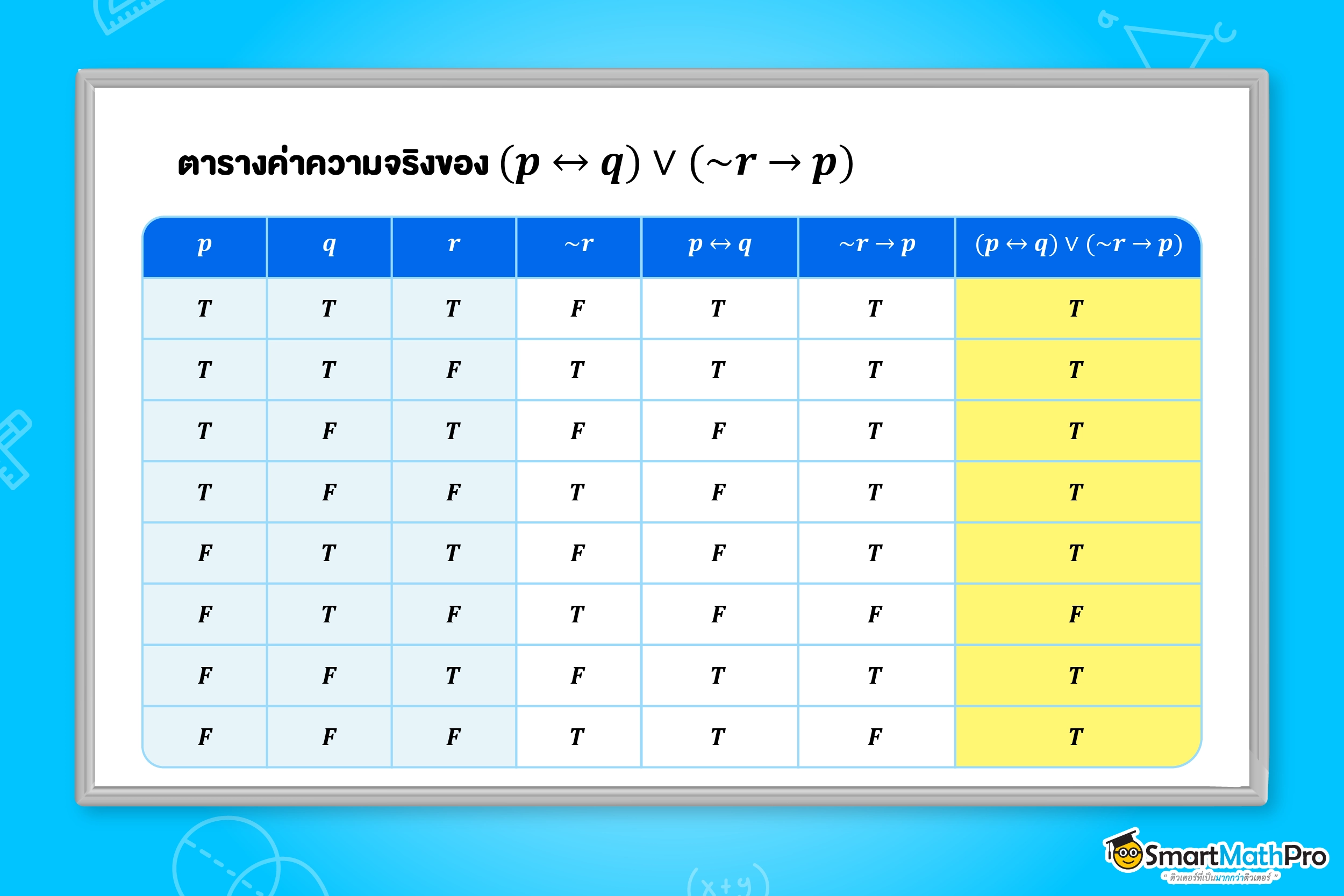
ตัวอย่างที่ 3 กำหนดให้ $p, q$ และ $r$ เป็นประพจน์ จงสร้างตารางค่าความจริงของ
$\left(p\leftrightarrow q\right)\vee\left(\sim r\rightarrow p\right)$

วิธีทำ

จากโจทย์มี $3$ ประพจน์ย่อย คือ $p, q$ และ $r$ ดังนั้นจะมีกรณีเกี่ยวกับค่าความจริงทั้งหมด $2^{n}=2^{3}=8$ กรณี

ตัวอย่างที่ 4 กำหนดให้ $p,q, r$ และ $s$ เป็นประพจน์ จงสร้างตารางค่าความจริงของ
$[\left(p\land q\right)\rightarrow r]\leftrightarrow s$

วิธีทำ

จากโจทย์มี $4$ ประพจน์ย่อย คือ $p, q,r$ และ $s$ ดังนั้นจะมีกรณีเกี่ยวกับค่าความจริงทั้งหมด $2^{n}=2^{4}=16$ กรณี

การหาค่าความจริงของประพจน์

รูปแบบของประพจน์ที่ประพจน์ย่อยยังไม่กำหนดค่าความจริง เราจะสร้างตารางค่าความจริงเพื่อดูค่าความจริงที่เป็นไปได้ทั้งหมด แต่เมื่อเราทราบค่าความจริงของประพจน์ย่อย เราจะสามารถสรุปค่าความจริงของรูปแบบประพจน์นั้น
ได้เลย

ตัวอย่างที่ 5 จงหาค่าความจริงของประพจน์ $(p\vee\sim q)\leftrightarrow r$ เมื่อ $p,q$ และ $r$ เป็นประพจน์ที่มีค่าความจริงเป็นเท็จ เท็จ และจริง ตามลำดับ

วิธีทำ

กำหนดให้ $T$ แทนจริง และ $F$ แทนเท็จ

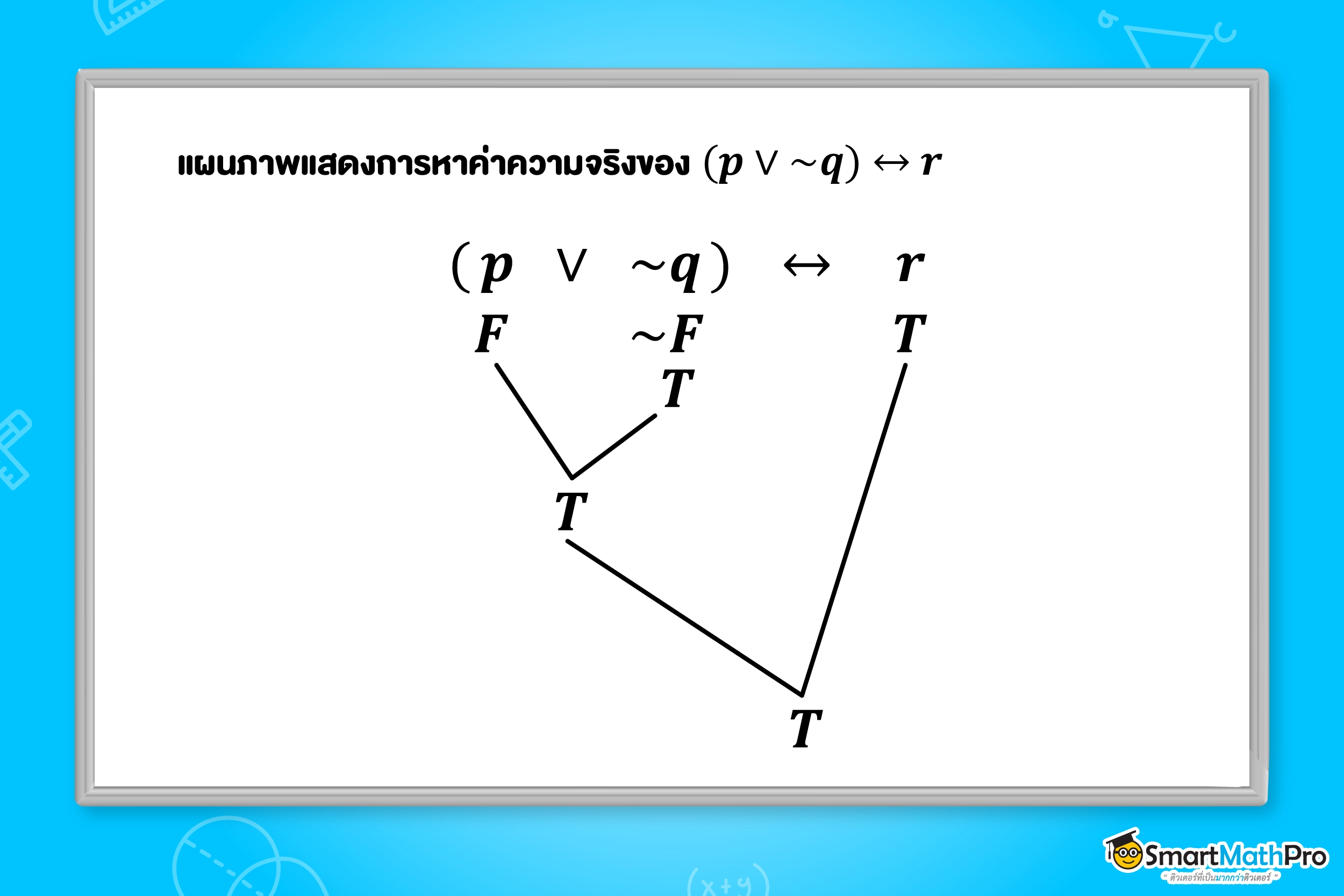
ดังนั้น ประพจน์ $(p\vee\sim q)\leftrightarrow r$ มีค่าความจริงเป็น จริง

ตัวอย่างที่ 6 กำหนดให้ประพจน์ $(p\rightarrow q)\ \vee(\sim p\vee r)$ มีค่าความจริงเป็นเท็จ จงหาค่าความจริงของประพจน์ $p,q$ และ $r$

วิธีทำ
กำหนดให้ $T$ แทนจริง และ $F$ แทนเท็จ

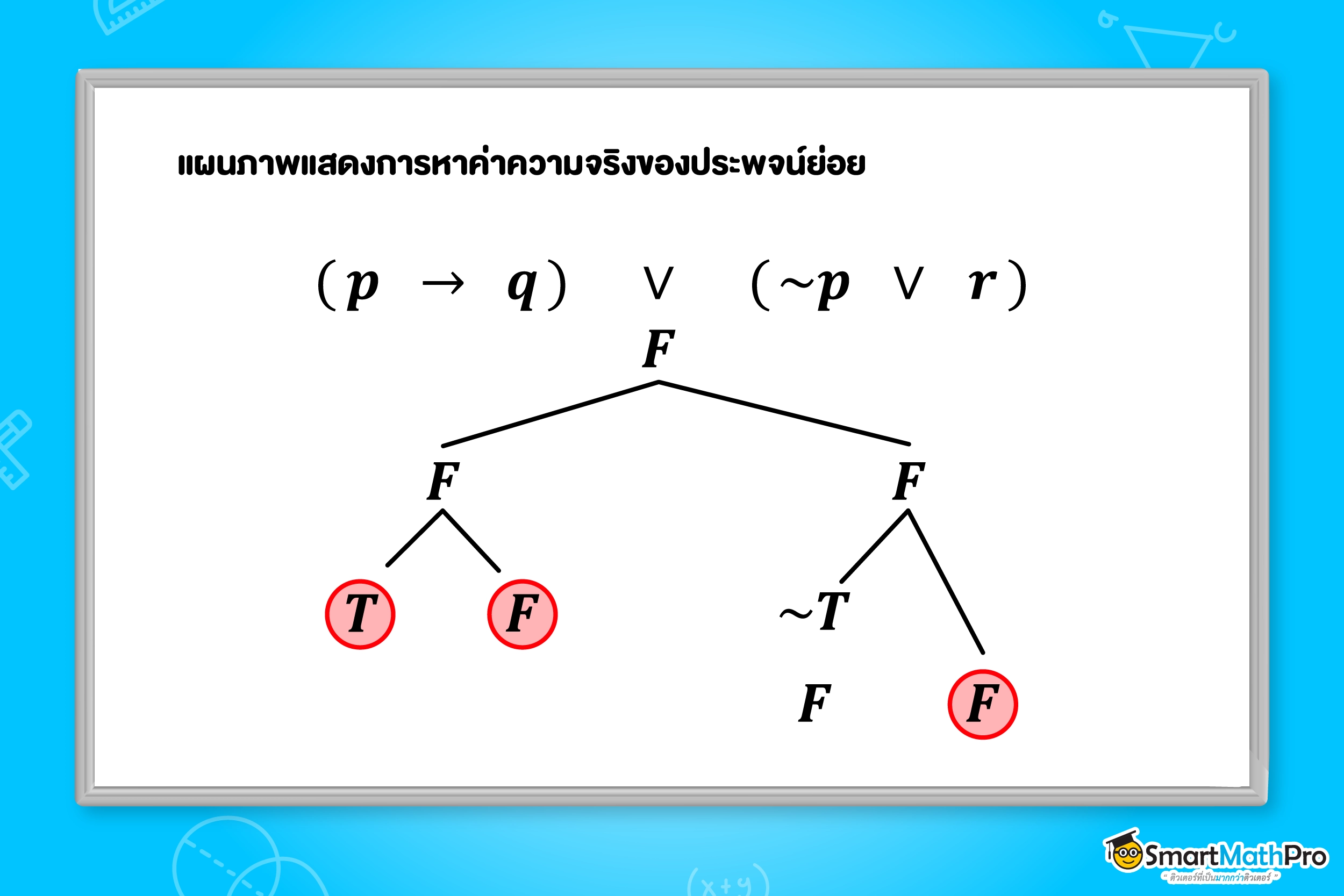
ดังนั้น $p\equiv T,\ q\equiv F$ และ $r\equiv F$

ติวคณิตศาสตร์ ม.ปลาย กับ SmartMathPro

เนื้อหาคณิตศาสตร์ ม.ปลาย อาจดูเป็นเรื่องยากในความคิดของน้อง ๆ หลายคน แต่ที่จริงถ้าเรามีพื้นฐานที่ดี ทบทวนบทเรียนและฝึกทำโจทย์บ่อย ๆ ก็จะทำให้เข้าใจในเนื้อหามากขึ้น แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์

พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%

โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย

ดูคลิปติวคณิต ม.4 เทอม 1 และ 2

ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro

พี่เชื่อว่าทุกคนน่าจะรู้จักเกี่ยวกับ “ตารางค่าความจริง”กันไปประมาณหนึ่งแล้ว และหวังว่าจะนำไปประยุกต์กับเนื้อหาที่เกี่ยวข้องได้น้าา อย่างไรก็ตามถ้าอยากจะเก่งเนื้อหานี้ให้มากขึ้น พี่แนะนำว่าให้ทบทวนเนื้อหาและควรฝึกทำโจทย์
บ่อย ๆ ด้วยย