สรุป ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม ม.4 พร้อมตัวอย่างโจทย์

น้อง ๆ อาจเคยได้ยินหรือรู้จักกับ “ฟังก์ชัน” กันมาแล้วในบทเรียนก่อนหน้านี้อย่างความสัมพันธ์และฟังก์ชัน ซึ่งบทเรียนในวันนี้เราก็ยังอยู่ที่คณิต ม.4 เทอม 2 และเป็นบทที่เกี่ยวกับฟังก์ชัน อย่างฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม ม.4

หลายคนพอได้ยินชื่อแล้วอาจจะคิดว่ามันต้องยากแน่ ๆ ใช่มั้ยย แต่พี่จะบอกว่ามันไม่ยากอย่างที่คิดเลย ถ้าเรามีพื้นฐานความรู้เรื่องเลขยกกำลังในระดับ ม.ต้นกับเรื่องความสัมพันธ์และฟังก์ชัน ซึ่งวันนี้พี่จะมาทวนความรู้เดิมและพาไปทำความเข้าใจเรื่อง ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม กันแบบจัดเต็ม แถมยังมีตัวอย่างโจทย์และแบบฝึกหัดให้ไปลองทำกันด้วยย

สนใจหัวข้อไหน ... กดอ่านเลย

ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม

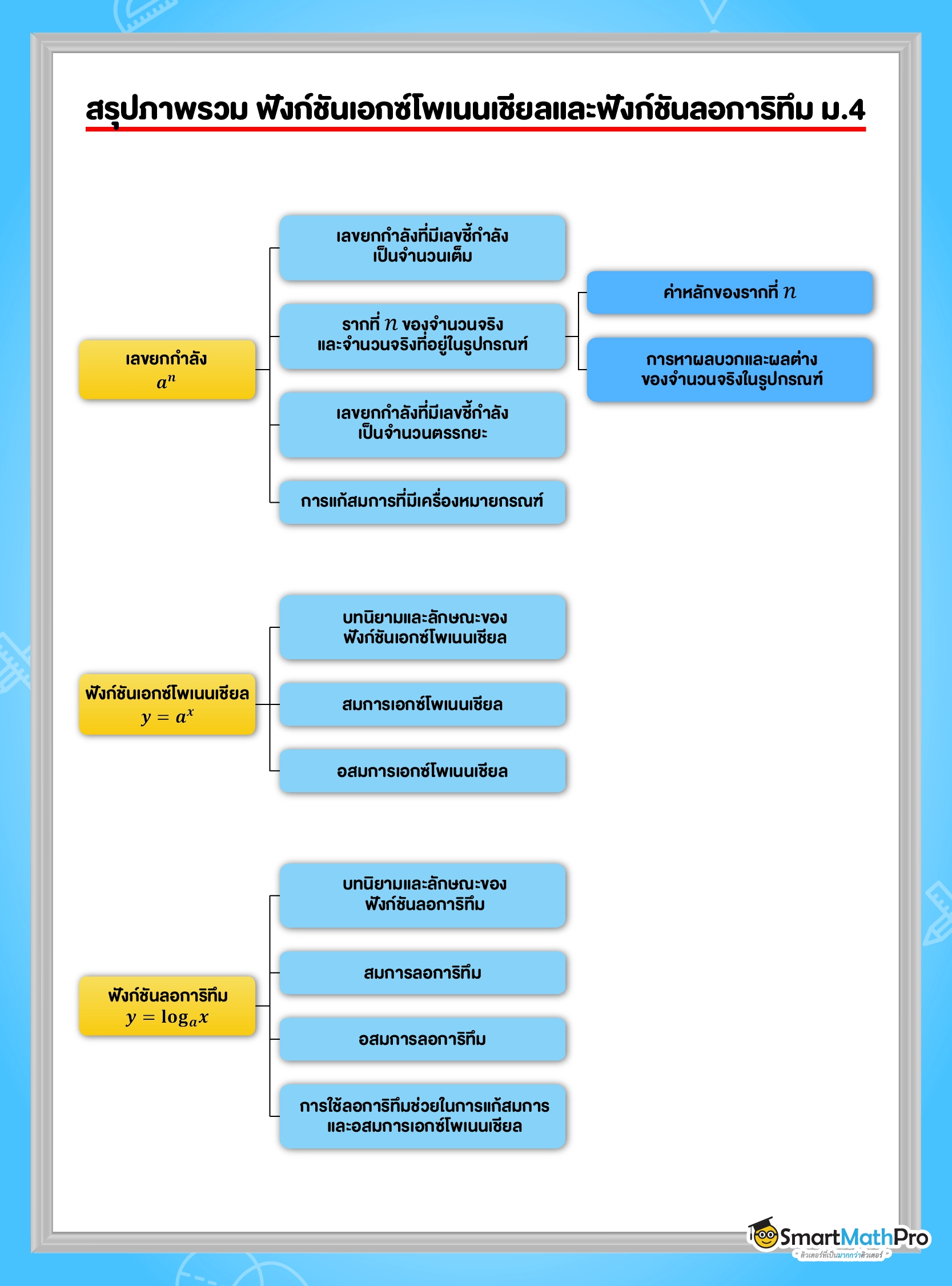
เลขยกกำลัง

น้อง ๆ น่าจะเคยเรียนเรื่องเลขยกกำลังมาแล้ว ตอนม.ต้น เกี่ยวกับความหมายของเลขยกกำลัง การคูณและการหารเลขยกกำลัง การเขียนสัญกรณ์วิทยาศาสตร์ รวมถึงสมบัติต่าง ๆ ของเลขยกกำลัง ในระดับชั้นม.5 นี้ เราจะมาทบทวนและเรียนเกี่ยวกับความหมายและสมบัติต่าง ๆ ของเลขยกกำลังอีกครั้ง แต่เป็นในแบบที่ท้าทายขึ้น มาลองดูกันเลย

บทนิยาม

ให้ $a$ เป็นจำนวนจริง และ $n$ เป็นจำนวนเต็มบวก

$a^n=a\times a\times a\times \cdots \times a$
( $a$ คูณกันทั้งหมด $n$ ตัว)

เรียก $a^n$ ว่า เลขยกกำลัง เรียก $a$ ว่า ฐานของเลขยกกำลัง และเรียก $n$ ว่า เลขชี้กำลัง

สมบัติเลขยกกำลัง

กำหนดให้ $a, b$ เป็นจำนวนจริงที่ไม่เป็นศูนย์ และ $m, n$ เป็นจำนวนตรรกยะ
• $a^0=1$
• $a^{-n}=\frac{1}{a^n}$
• $a^m\cdot a^n=a^{m+n}$
• $\frac{a^m}{a^n} =a^{m-n}$
• $\left (a^m \right )^{n}=a^{mn}$
• $\left ( ab \right )^{n}=a^n\cdot b^n$
• $\left (\frac{a}{b} \right )^{n}=\frac{a^n}{b^n}$

เราจะนำสมบัติเลขยกกำลังมาใช้เพื่อหาค่าหรือจัดรูป ลองมาดูการใช้สมบัติผ่านตัวอย่างนี้กัน

ตัวอย่างที่ 1 จงเขียน $\frac{\left ( 27^2\times 9^{-2} \right )^{3}}{3^{15}}$ ให้อยู่ในรูปอย่างง่าย และเลขยกกำลังทุกตัวมีเลขชี้กำลังเป็นจำนวนเต็มบวก
วิธีทำ

$\frac{\left ( 27^2\times 9^{-2} \right )^{3}}{3^{15}}$
$=\frac{\left ( \left ( 3^3 \right )^2\times ( \left ( 3^2 \right )^{-2} \right )^{3}}{3^{15}}$
$=\frac{3^{18}\times 3^{-12}}{3^{15}}$
$=\frac{3^{18}}{3^{27}}$
$=\frac{1}{3^{9}}$

รากที่ n ของจำนวนจริง และจำนวนจริงที่อยู่ในรูปกรณฑ์

บทนิยาม
กำหนดให้ $x$ และ $y$ เป็นจำนวนจริง และ $n$ เป็นจำนวนเต็มที่มากกว่า 1

รากที่ $n$ ของจำนวนจริง
$y$ เป็นรากที่ $n$ ของ $x$ ก็ต่อเมื่อ $y^n=x$
ค่าหลักของรากที่ $n$
$y$ เป็นค่าหลักของรากที่ $n$ ของ $x$ ก็ต่อเมื่อ
$y$ เป็นรากที่ $n$ ของ $x$ และ $xy\geq 0$

พี่ขอยกตัวอย่างเพิ่มเติมจากบทนิยาม จะได้ว่า
• รากที่ 2 ของ 9 คือ 3 และ -3
• รากที่ 5 ของ -32 คือ -2
• ค่าหลักของรากที่ 2 ของ 36 คือ 6
• $\sqrt{36}=6$
จะเห็นได้ว่า ค่าหลักของรากที่ $n$ ของ $x$ มีค่าเท่ากับ กรณฑ์ที่ $n$ ของ $x$
นั่นคือค่าหลักของรากที่ $n$ ของ $x$ = $\sqrt[n]{x}$

ตัวอย่างที่ 2 $\frac{\sqrt{4}\cdot \sqrt[3]{5^3}}{\sqrt[3]{-8}}+\sqrt{\left ( -7 \right )^{2}}$ เท่ากับเท่าใด
วิธีทำ $\frac{\sqrt{4}\cdot \sqrt[3]{5^3}}{\sqrt[3]{-8}}+\sqrt{\left ( -7 \right )^{2}}$
$=\frac{2\cdot 5}{-2}+\sqrt{49}$
$=-5+7$
$=2$

ฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันเอกซ์โพเนนเชียล คือ ฟังก์ชันที่อยู่ในรูป $\left \{ (x,y) \in \mathbb{R\times \mathbb{R}}|y=a^{x}\right \}$
โดยที่ $a$ เป็นจำนวนจริง ซึ่ง $a>0$ และ $a\neq 1$

พิจารณาลักษณะกราฟของฟังก์ชันเอกซ์โพเนนเชียล

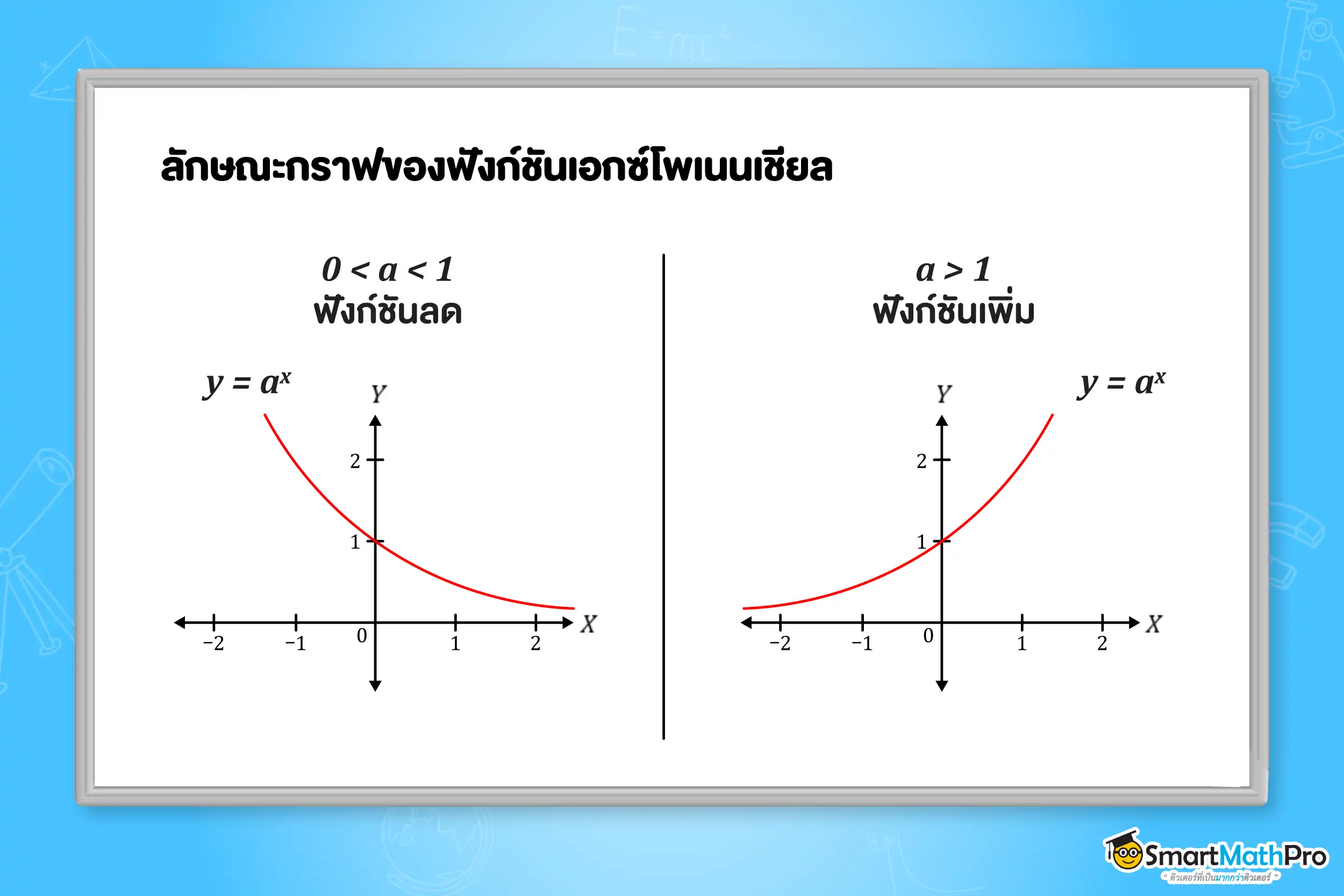
จากกราฟน้องจะเห็นว่าฟังก์ชันเอกซ์โพเนนเชียลจะเป็นฟังก์ชันเพิ่มหรือฟังก์ชันลดนั้นขึ้นอยู่กับค่า $a$

ตัวอย่างที่ 3 จงเขียนกราฟของฟังก์ชัน $f(x)=3^{x}$ และ $g(x)=\left ( \frac{1}{3} \right )^{x}$ ลงในระบบพิกัดฉากเดียวกัน

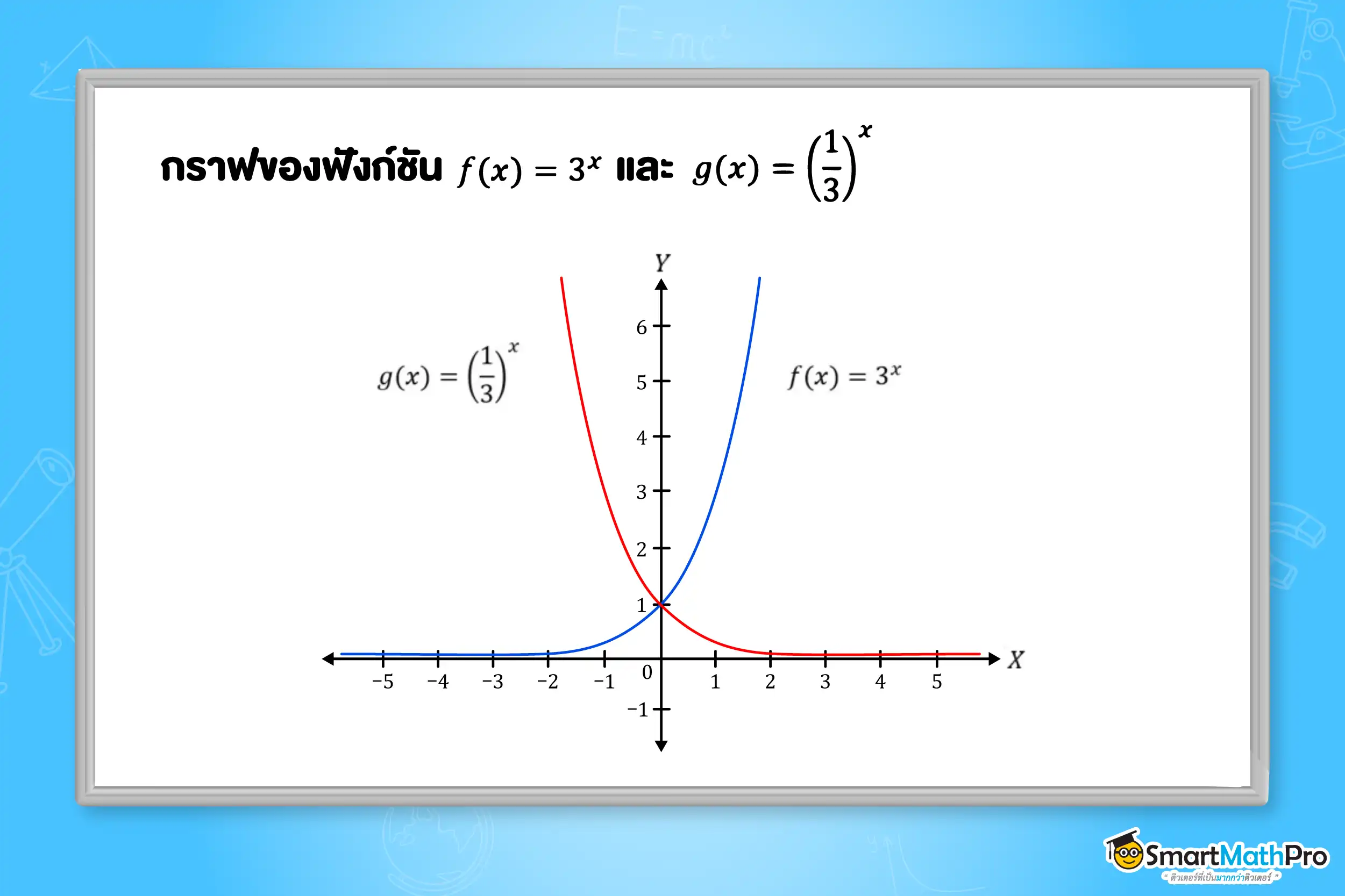
จากกราฟที่เราได้ น้องจะเห็นว่า $f(x)=3^{x}$ เป็นฟังก์ชันเพิ่มเพราะ $a$ มีค่ามากกว่า 1 และ $g(x)=\left ( \frac{1}{3} \right )^{x}$ เป็นฟังก์ชันลดเพราะ $a$ มีค่าอยู่ระหว่าง 0 กับ 1 นั่นเอง

ตัวอย่างที่ 4 กำหนดฟังก์ชัน $f(x)=2^{x}$ จงพิจารณาว่ากราฟของฟังก์ชันต่อไปนี้เกิดจากการเลื่อนจุดทุกจุดของฟังก์ชัน $f(x)$ อย่างไร
1. $g(x)=2^{x}+1$
ตอบ กราฟของ $g(x)$ คือกราฟของ $f(x)$ ที่เลื่อนจุดทุกจุดขึ้น 1 หน่วย

2. $h(x)=2^{x+1}$
ตอบ กราฟของ $h(x)$ คือกราฟของ $f(x)$ ที่เลื่อนจุดทุกจุดไปทางซ้าย 1 หน่วย

จากตัวอย่างที่ 4 น้อง ๆ อาจคิดว่า การพิจารณาว่ากราฟเลื่อนไปทางไหนซับซ้อน แต่การเลื่อนกราฟไม่ใช่เรื่องยากอย่างที่คิดนะ พี่ก็ได้สรุปเรื่องการเลื่อนกราฟมาให้แล้ว มาดูกันเลย

กราฟ $y=a^{(x-h)}+k$ คือการเลื่อนกราฟ $y=a^{x}$ ดังนี้

ถ้า $h$ มีค่าเป็นบวกจะเลื่อนจุดทุกจุดไปทางขวา $h$ หน่วย
ถ้า $h$ มีค่าเป็นลบจะเลื่อนจุดทุกจุดไปทางซ้าย $h$ หน่วย
ถ้า $k$ มีค่าเป็นบวกจะเลื่อนจุดทุกจุดขึ้น $k$ หน่วย
ถ้า $k$ มีค่าเป็นลบจะเลื่อนจุดทุกจุดลง $k$ หน่วย

หลังจากที่เรารู้จักว่าฟังก์ชันเอกซ์โพเนนเชียลไปแล้ว เรามารู้จักสมการและอสมการเอกซ์โพเนนเชียลกันบ้าง ซึ่งก็คือสมการและอสมการที่มีเลขชี้กำลังเป็นตัวแปรนั่นเอง ในการแก้สมการและอสมการจะใช้สมบัติความเป็นฟังก์ชัน 1-1 ฟังก์ชันเพิ่มและฟังก์ชันลดด้วยน้า

สมการเอกซ์โพเนนเชียล

หลักการแก้สมการเอกซ์โพเนนเชียล มีดังนี้
• ให้ $a>0$ และ $a\neq 1$ จะได้ว่า $a^{x}=a^{y}$ ก็ต่อเมื่อ $x=y$
• ให้ $a,b>0$ โดยที่ $a\neq b$ ถ้า $a^{x}=b^{x}$ แล้ว $x=0$

สรุปง่าย ๆ ก็คือถ้าฐานมีค่าเท่ากันแล้วเลขชี้กำลังจะมีค่าเท่ากัน และถ้าเลขชี้กำลังมีค่าเท่ากันแต่ฐานมีค่าไม่เท่ากันแล้วเลขชี้กำลังจะเท่ากับ $0$ นั่นเอง

ตัวอย่างที่ 5 จงหาเซตคำตอบของสมการต่อไปนี้
1. $2^{2x}=4^{8}$
วิธีทำ จะได้ว่า $2^{2x}=(2^{2})^{8}$
$2^{2x}=2^{16}$
$2x=16$
$x=8$
ดังนั้น เซตคำตอบของสมการ คือ $\left \{ 8 \right \}$

2. $3^{10x+2}=4^{5x+1}$
วิธีทำ จะได้ว่า $3^{10x+2}=(2^{2})^{5x+1}$
$3^{10x+2}=2^{10x+2}$
$10x+2=0$
$x=-\frac{1}{5}$
ดังนั้น เซตคำตอบของสมการ คือ $\left \{-\frac{1}{5} \right \}$

อสมการเอกซ์โพเนนเชียล

หลักการแก้อสมการเอกซ์โพเนนเชียล มีดังนี้
1. อสมการ $a^{m}>a^{n}$

ถ้า $a>1$ แล้ว $m>n$
ถ้า $0<a<1$ แล้ว $m<n$

2. อสมการ $a^{m}<a^{n}$

ถ้า $a>1$ แล้ว $m<n$
ถ้า $0<a<1$ แล้ว $m>n$

สังเกตได้ว่า ถ้าฐานมีค่าอยู่ระหว่าง 0 ถึง 1 จะต้องกลับเครื่องหมายของอสมการด้วยน้า

ตัวอย่างที่ 6 จงหาคำตอบของอสมการต่อไปนี้
1. $10^{3x}>1000$
วิธีทำ จะได้ว่า $10^{3x}>10^{3}$
$3x>3$
ดังนั้น $x>1$

2. $\left (\frac{1}{3} \right )^{2x+1}<\frac{1}{27}$
วิธีทำ จะได้ว่า $\left (\frac{1}{3} \right )^{2x+1}<\left (\frac{1}{3} \right )^{3}$
$2x+1>3$
$2x>2$
ดังนั้น $x>1$

ฟังก์ชันลอการิทึม

ฟังก์ชันลอการิทึม คือ ฟังก์ชันที่อยู่ในรูป $\left \{(x, y)\in \mathbb{R}^+\times \mathbb{R} \mid y=\log_a{x} \right \}$
โดยที่ $a$ เป็นจำนวนจริง ซึ่ง $a>0$ และ $a \neq 1$
ฟังก์ชันลอการิทึม คือ ตัวผกผันของฟังก์ชันเอกซ์โพเนนเชียล นั่นคือ
$x=a^y$ ก็ต่อเมื่อ $y=\log_a{x}$

ลักษณะกราฟของฟังก์ชันลอการิทึมเป็นดังนี้

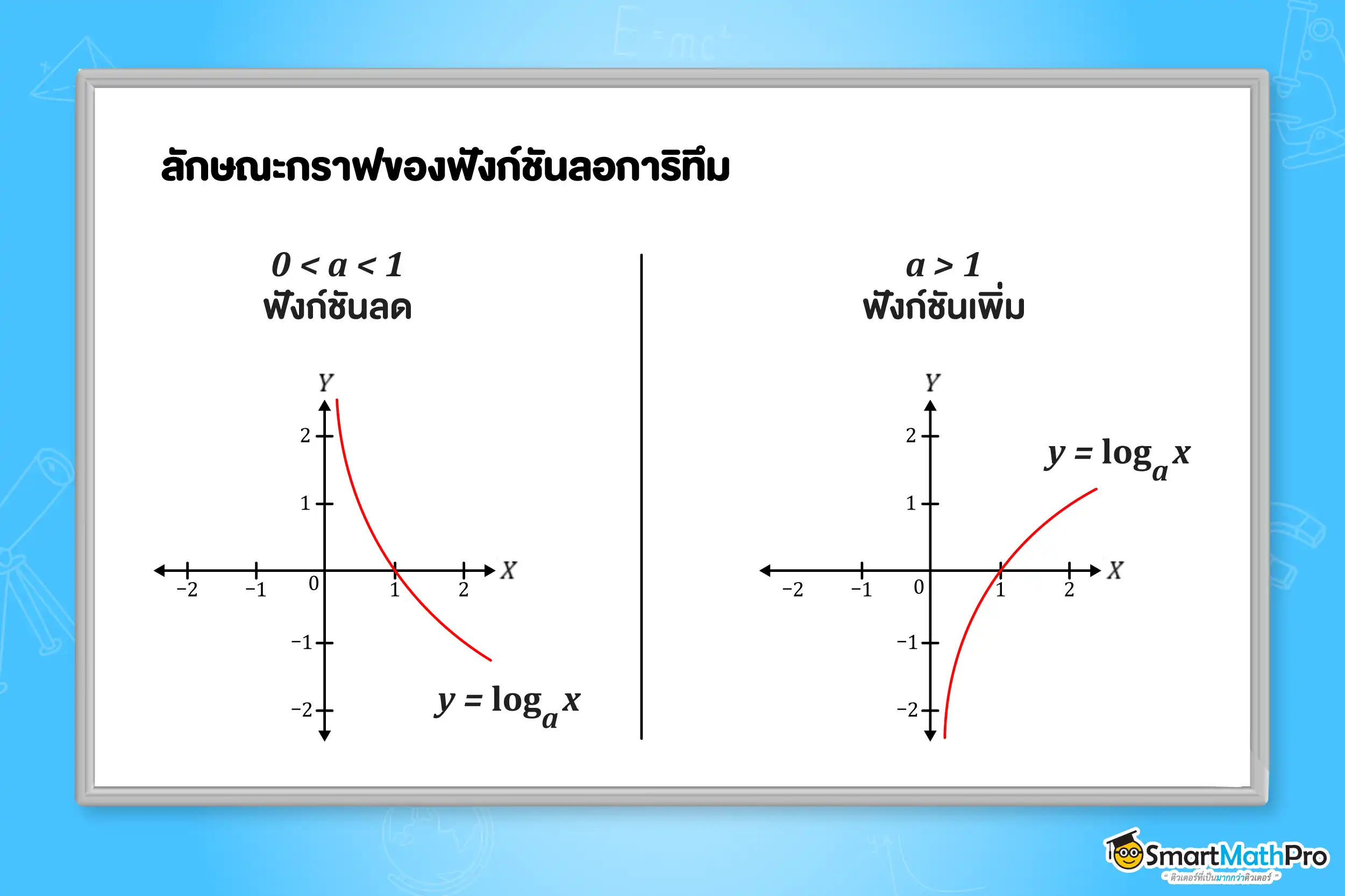
จากกราฟ น้องจะเห็นว่าฟังก์ชันลอการิทึมจะเป็นฟังก์ชันเพิ่มหรือฟังก์ชันลดนั้นขึ้นอยู่กับค่า $a$

ตัวอย่างที่ 7 กำหนด $f(x)=\log_2{x}$ จงพิจารณาว่ากราฟของฟังก์ชันต่อไปนี้เกิดจากการเลื่อนจุดทุกจุดของฟังก์ชัน $f(x)$ อย่างไร
แนวคิด ใช้วิธีการเลื่อนกราฟคล้ายตัวอย่างที่ 4 เลย !

$g(x)=\log_{2}(x)-1$
ตอบ กราฟของ $g(x)$ คือกราฟของ $f(x)$ ที่เลื่อนจุดทุกจุดลง 1 หน่วย
$h(x)=\log_2{(x-1)}$
ตอบ กราฟของ $h(x)$ คือกราฟของ $f(x)$ ที่เลื่อนจุดทุกจุดไปทางขวา 1 หน่วย

สมบัติของฟังก์ชันลอการิทึม

ให้ $a, M$ และ $N$ เป็นจำนวนจริงบวกที่ $a\neq1$
และ $k$ เป็นจำนวนจริง จะได้ว่า

$\log_a{a}=1$ และ $\log_a{1}=0$
$\log_a{MN}=\log_a{M}+\log_a{N}$
$\log_a{\frac{M}{N}}=\log_a{M}-\log_a{N}$
$\log_a{M^k}=k\log_a{M}$
$\log_{a^k}{M}=\frac{1}{k}\log_a{M}$
เมื่อ $k\neq0$
$\log_a{b}=\frac{1}{\log_b{a}}$
เมื่อ $b>0$ และ $b\neq1$
$\log_a{M}=\frac{\log_c{M}}{\log_c{a}}$
เมื่อ $c>0$ และ $c\neq1$
$a^{\log_b{c}}=c^{\log_b{a}}$

ตัวอย่างที่ 8 จงหาค่าของ $\log_4{32}+\log_4{2}$
วิธีทำ
$\log_4{32}+\log_4{2}$
$=\log_4({32\times 2})$
$=\log_4{64}$
$=\log_4{4^3}$
$=3\times \log_4{4}$
$=3\times 1$
$=3$

มุมความรู้

เมื่อ $\log$ ไม่ได้เขียนเลขฐานจะถือว่าเป็น ฐาน $10$

สมการลอการิทึม

หลักการแก้สมการลอการิทึม มีดังนี้
1. ให้ $a>0$ และ $a\neq1$ จะได้ว่า $\log_a{x}=\log_a{y}$ ก็ต่อเมื่อ $x=y$
2. จาก $\log_a{x}=y$ จะได้ว่า $x=a^y$

ตัวอย่างที่ 9 จงหาเซตคำตอบของสมการ $\log(x-1)+\log(x+2)=1$
วิธีทำ
$\log(x-1)+\log(x+2)=1$
$(x-1)(x+2)=10$
$x^2+x-2=10$
$x^2+x-12=0$
$(x+4)(x-3)=0$
จะได้ว่า $x=-4$ หรือ $x=3$

ตรวจสอบค่า $x$ ที่ได้ว่าค่าใดสอดคล้องกับสมการที่กำหนดให้

กรณี $x=-4$
แทน $x=-4$ ใน $\log(x-1)+\log(x+2)=1$
จะได้ $\log(-5)+\log(-2)=1$ เป็นเท็จ
เนื่องจากไม่นิยาม $y=\log_a{x}$ เมื่อ $x$ ไม่เป็นจำนวนจริงบวก
แสดงว่า $-4$ ไม่สอดคล้องกับสมการที่กำหนดให้
กรณี $x=3$
แทน $x=3$ ใน $\log(x-1)+\log(x+2)=1$
จะได้ $\log(2)+\log(5)=\log(5\times2)=\log10=1$ เป็นจริง
แสดงว่า $3$ สอดคล้องกับสมการที่กำหนดให้

ดังนั้น เซตคำตอบของสมการ คือ $\left \{ 3 \right \}$

ระวัง!! อย่าลืมเช็กเสมอว่าคำตอบที่ได้จากการแก้สมการ ทำให้หลัง log ติดลบหรือไม่ด้วยน้าา

อสมการลอการิทึม

หลักการแก้อสมการลอการิทึม มีดังนี้
1. อสมการ $\log_a{m} > \log_a{n}$

ถ้า $a>1$ แล้ว $m>n$
ถ้า $0<a<1$ แล้ว $m<n$

2. อสมการ $\log_a{m} < \log_a{n}$

ถ้า $a>1$ แล้ว $m<n$
ถ้า $0<a<1$ แล้ว $m>n$

ตัวอย่างที่ 10 จงหาเซตคำตอบของอสมการ $\log_\frac{1}{2}(x+2)-\log_\frac{1}{2}(x+1)<2$
วิธีทำ
$\log_\frac{1}{2}(x+2)-\log_\frac{1}{2}(x+1)<2$
$\log_{\frac{1}{2}}\left (\frac{x+2}{x+1} \right )<2\log_{\frac{1}{2}}\left (\frac{1}{2} \right )$
$\log_{\frac{1}{2}}\left (\frac{x+2}{x+1} \right )<\log_{\frac{1}{2}}\left (\frac{1}{2} \right )^2$
$\log_{\frac{1}{2}}\left (\frac{x+2}{x+1} \right )<\log_{\frac{1}{2}}\left (\frac{1}{4} \right )$

เนื่องจาก $f(x)=\log_\frac{1}{2}{x}$ เป็นฟังก์ชันลด
$\frac{x+2}{x+1}>\frac{1}{4}$
$\frac{x+2}{x+1}-\frac{1}{4}>0$
$\frac{4(x+2)-(x+1)}{4(x+1)}>0$
$\frac{3x+7}{4x+4}>0$

จะได้ $x<-\frac{7}{3}$ และ $x>-1$
เนื่องจาก อสมการที่กำหนดให้มีพจน์ $\log_\frac{1}{2}(x+2)$ และ $\log_\frac{1}{2}(x+1)$
จะได้ว่า $x>-2$ และ $x>-1$
นั่นคือ $x>-1$

ดังนั้น เซตคำตอบของอสมการ คือ $\left ( -1, \infty \right )$

ระวัง !! อย่าลืมเช็กเสมอว่าคำตอบที่ได้จากการแก้อสมการ ทำให้หลัง log ติดลบหรือไม่ด้วยน้าา และถ้าฐานน้อยกว่า 1 แต่มากกว่า 0 แล้ว ต้องกลับเครื่องหมายอสมการนั้นด้วยนะ

ดูคลิปติวฟรี ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม ม.4

ดูคลิปติวฟรีอื่น ๆ ได้ที่ YouTube : SmartMathPro

เป็นยังไงบ้างสำหรับสรุปเนื้อหาที่พี่เอามาฝากน้อง ๆ ทุกคนในวันนี้ ใครที่ยังไม่เข้าใจก็สามารถไปดูคลิปติวฟรีของพี่ใน Youtube ได้นะ หรือจะกลับไปทบทวนความรู้เดิมจากบทเลขยกกำลังในคณิต ม.ต้น กับบทเรียนก่อนหน้าอย่าง
ความสัมพันธ์และฟังก์ชันก็ได้ จะได้แม่นเนื้อหากันมากขึ้น

นอกจากนี้วิธีที่พี่อยากแนะนำเพิ่มคือ ให้ลองฝึกทำโจทย์ เพื่อเป็นการทบทวนความเข้าใจของตัวเอง ซึ่งถ้าใครไม่รู้จะไปหาโจทย์จากไหนมาฝึกทำซ้อมมือ ก็สามารถเข้าไปดาวน์โหลดข้อสอบได้ในคลังข้อสอบเลยย ค่อย ๆ ทำความเข้าใจกันไปน้า ไม่ต้องรีบหรือเร่งตัวเองมากเกินไป

เนื้อหาคณิตศาสตร์ ม.ปลาย อาจดูเป็นเรื่องยากในความคิดของน้อง ๆ หลายคน แต่ที่จริงถ้าเรามีพื้นฐานที่ดี ทบทวนบทเรียนและฝึกทำโจทย์บ่อย ๆ ก็จะทำให้เข้าใจในเนื้อหามากขึ้น แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์

พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%

โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย