สรุปพื้นที่ผิวและปริมาตร (พีระมิด กรวย และทรงกลม) ม.3 พร้อมโจทย์+เฉลย

เนื้อหาเรื่องพื้นที่และปริมาตร เป็นเนื้อหาที่หลายคนน่าจะคุ้น ๆ เพราะเราเคยเจอแล้วในชั้น ม.2 คือ ปริซึมและทรงกระบอก แต่สำหรับคณิต ม.3 นั้น เราจะเรียนเกี่ยวกับพีระมิด กรวย และทรงกลม
โดยในบทความนี้ พี่จะพาน้อง ๆ ไปรู้จักพีระมิด กรวย และทรงกลมให้มากยิ่งขึ้น ทั้งเรื่องความหมาย, พื้นที่ผิว, ปริมาตร และสูตร พร้อมแจกแบบฝึกหัด+เฉลยให้น้อง ๆ ได้ลองทำกันท้ายบทความด้วยน้าา

สนใจหัวข้อไหน ... กดอ่านเลย

ทบทวนความรู้เรื่องรูปเรขาคณิตสองมิติ ปริซึมและทรงกระบอก

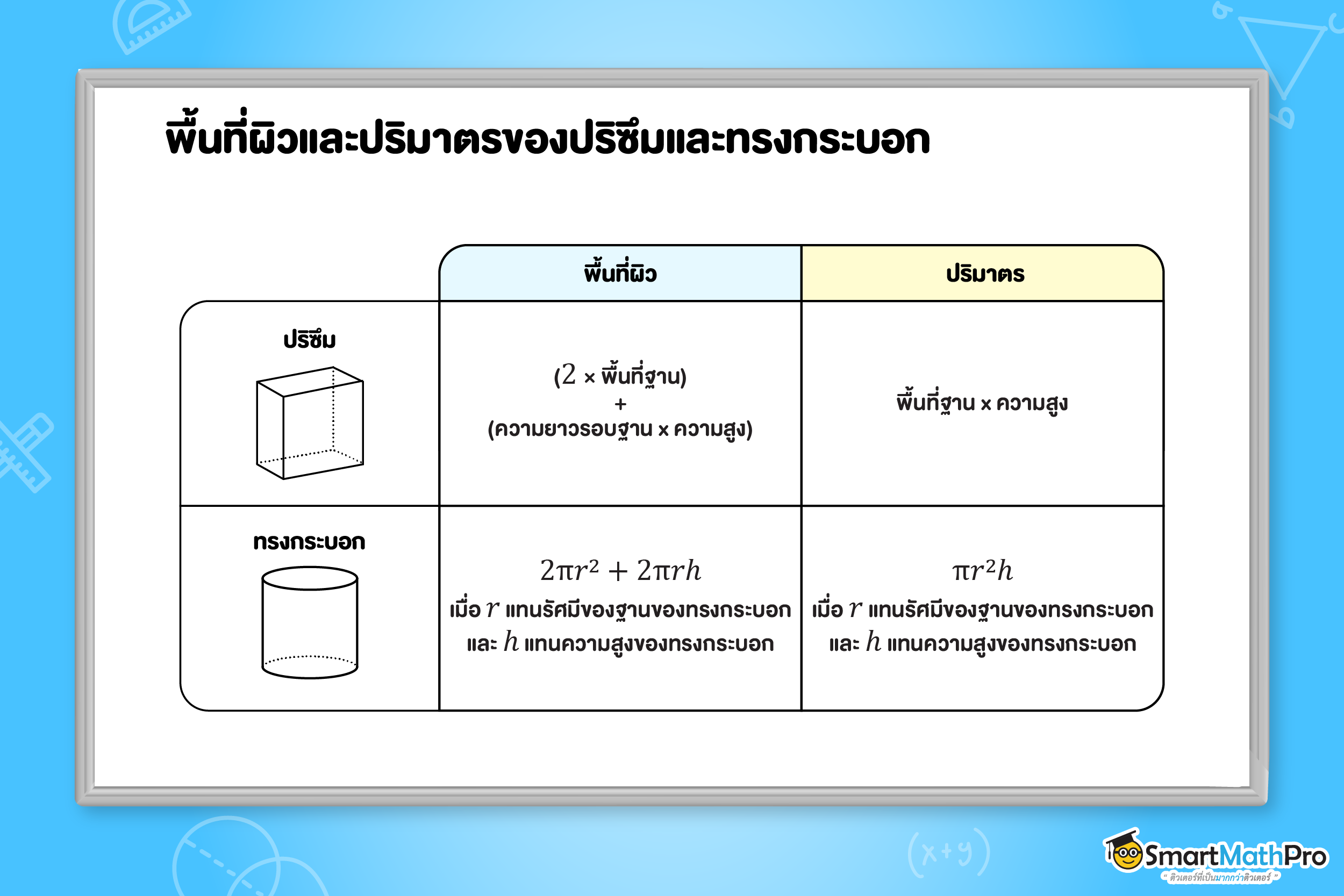
ก่อนที่เราจะไปเข้าสู่หัวข้อ พีระมิด กรวย ทรงกลม ม.3 เรามาทบทวนความรู้ก่อนหน้าที่น่ารู้ในบทนี้ ทั้งสูตรการหาพื้นที่รูปเรขาคณิต และ ปริซึมและทรงกระบอก ม.2

พีระมิด คืออะไร ?

โดยทั่วไปเมื่อกล่าวถึง “พีระมิด” ภาพแรกที่เรานึกถึงมักจะเป็นพีระมิดในประเทศอียิปต์ซึ่งฐานเป็นรูปสี่เหลี่ยมจัตุรัส แต่ในทางคณิตศาสตร์และในชีวิตประจำวันไม่เป็นเช่นนั้น ฐานของพีระมิดไม่จำเป็นต้องมีฐานเป็นรูปสี่เหลี่ยมจัตุรัสเสมอไป

ในทางคณิตศาสตร์ รูปเรขาคณิตที่มีฐานเป็นรูปเหลี่ยมใด ๆ มียอดแหลมที่ไม่อยู่บนระนาบเดียวกันกับฐาน
และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น เรียกว่า พีระมิด (pyramid)

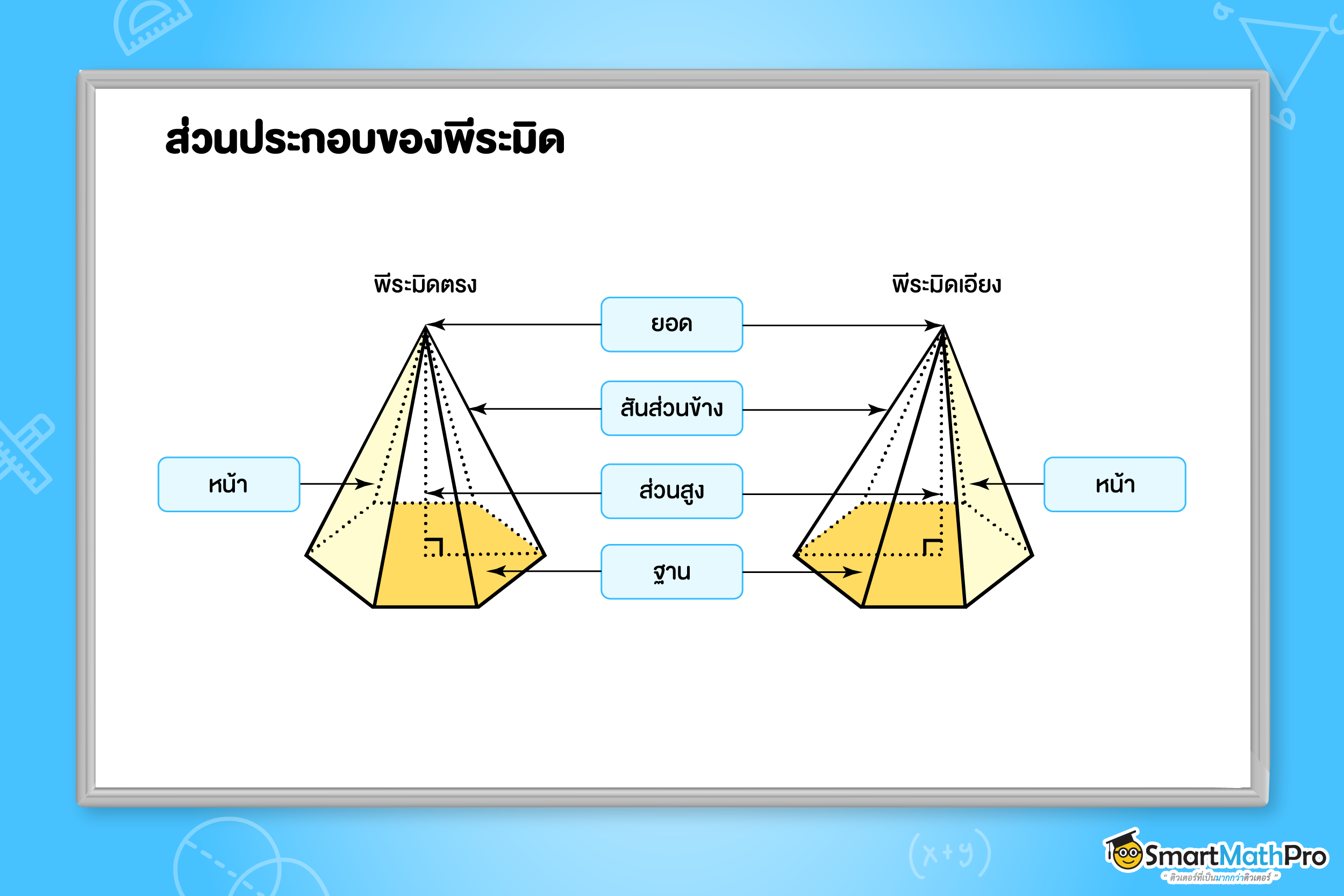
ในระดับชั้นนี้เราจะกล่าวเฉพาะพีระมิดตรง (right pyramid) ซึ่งเป็นพีระมิดที่มีส่วนสูงตั้งฉากกับฐานที่จุดศูนย์กลางของรูปหลายเหลี่ยมนั้น ๆ และเรียกจุดดังกล่าวว่าเซนทรอยด์ (centroid) โดยเราจะเรียกส่วนประกอบของปริซึมในแต่ละส่วน ดังรูปนี้

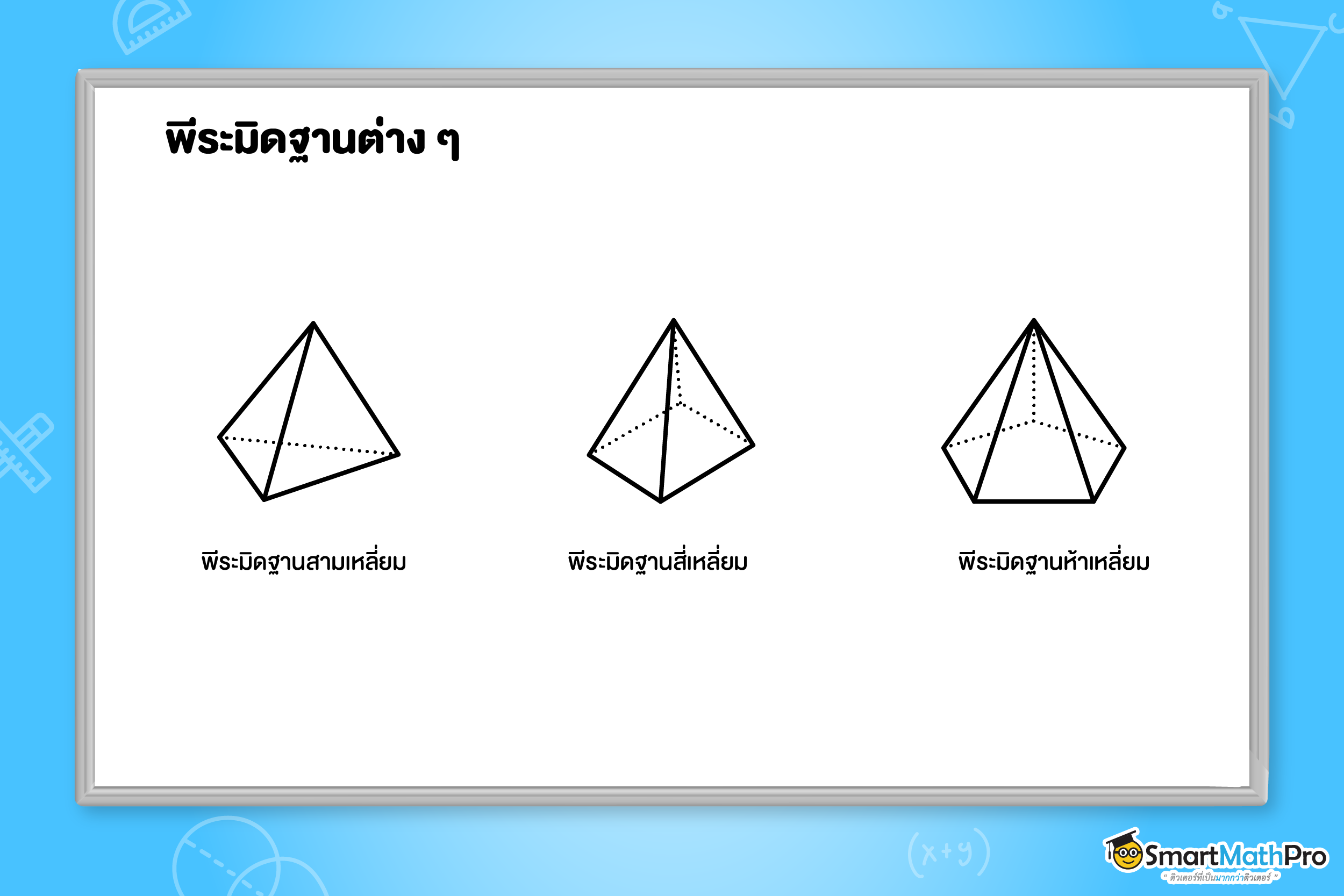
จะเรียกชื่อพีระมิดต่าง ๆ ตามลักษณะของฐานของพีระมิด ดังนี้

พื้นที่ผิวของพีระมิด

จากชั้น ม.2 น้อง ๆ เคยเรียนการหาพื้นที่ผิวของปริซึมและทรงกระบอกมาแล้ว การหาพื้นที่ผิวของพีระมิดสามารถคำนวณหาได้จากพื้นที่ฐานและพื้นที่ผิวข้างของรูปพีระมิด โดยการวาดของรูปคลี่ของพีระมิดได้เช่นกัน ลองพิจารณาการหาพื้นที่ผิวของพีระมิดฐานสี่เหลี่ยมต่อไปนี้

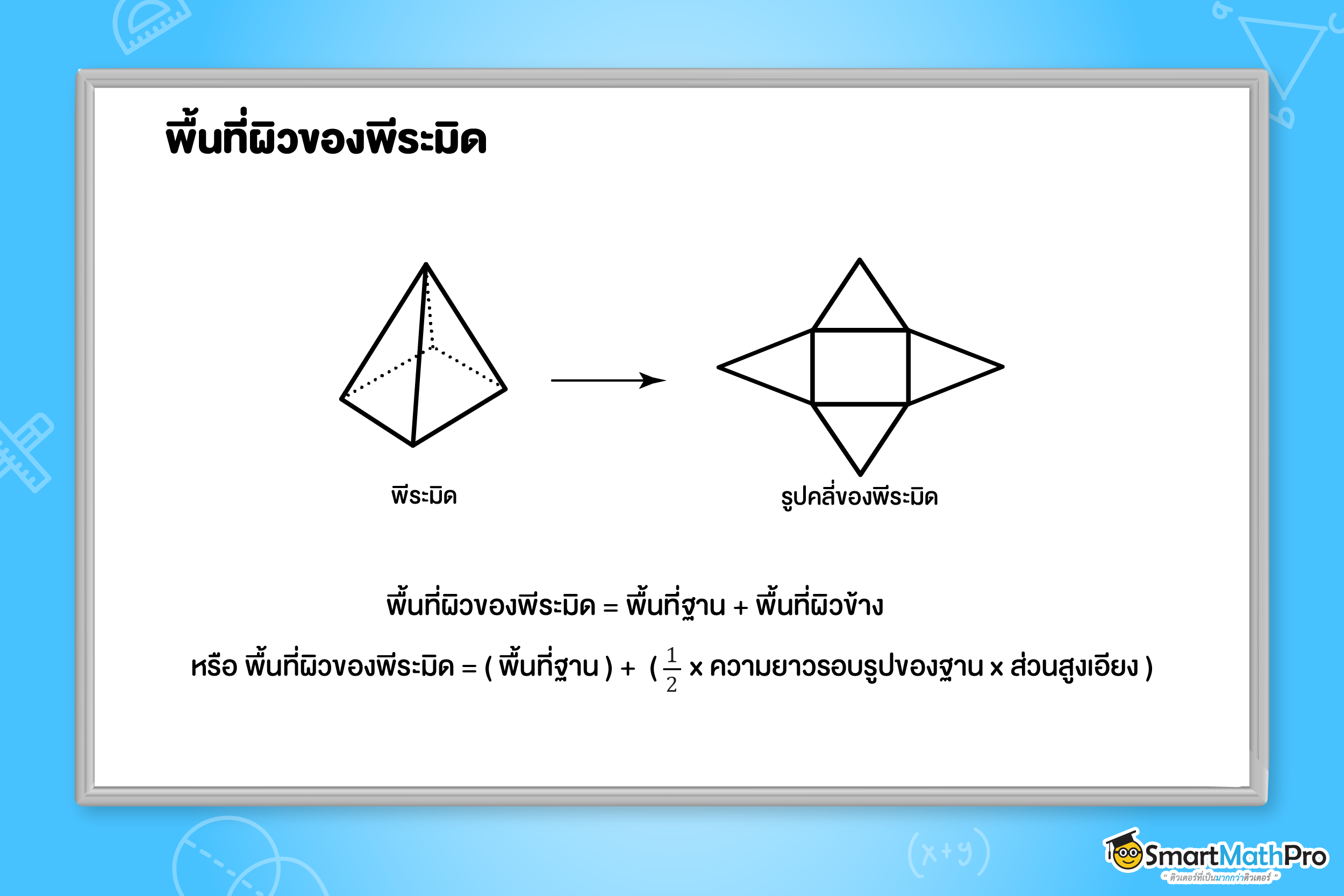
เพื่อให้น้อง ๆ เข้าใจการหาพื้นที่ผิวของพีระมิดและเห็นภาพมากขึ้น เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กัน

ตัวอย่างที่ 1 จากรูป จงหาพื้นที่ผิวของพีระมิดฐานสี่เหลี่ยมจัตุรัสต่อไปนี้

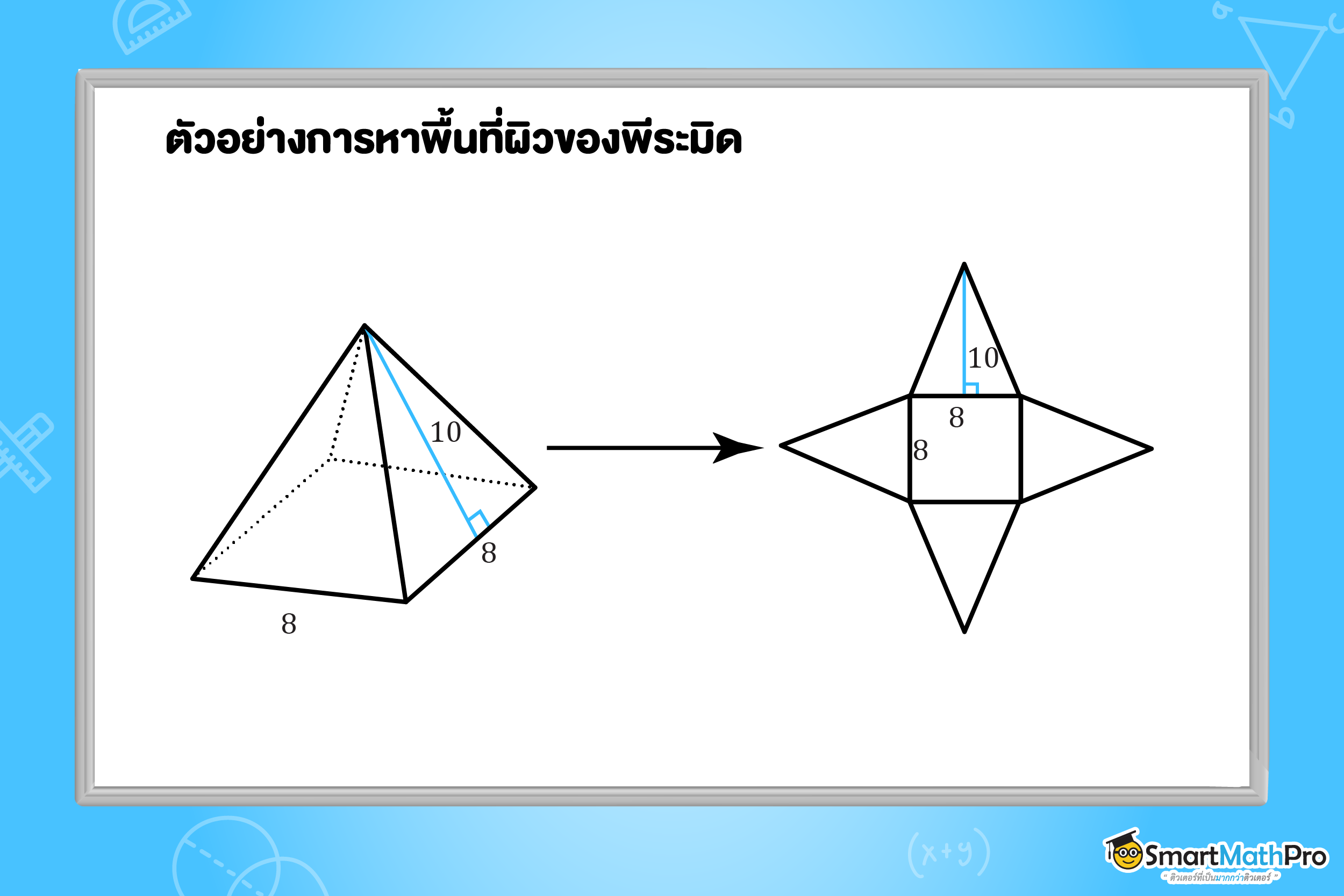
วิธีทำ จากรูป ฐานพีระมิดเป็นรูปสี่เหลี่ยมจัตุรัส ที่มีทุกด้านยาว $8$ หน่วย
จะได้ พื้นที่ฐาน $=8\times8=64$ ตารางหน่วย
พื้นที่ผิวข้าง เป็นรูปสามเหลี่ยมที่มีฐานยาว $8$ หน่วย และสูง $10$ หน่วย ทั้งหมด $4$ รูป
จะได้ พื้นที่ผิวข้าง $=\left(\frac{1}{2}\times8\times10\right)\times4=160$ ตารางหน่วย
ดังนั้น พื้นที่ผิวของพีระมิดนี้ คือ $64+160=224$ ตารางหน่วย

ปริมาตรของพีระมิด

แนวคิดการหาปริมาตรของพีระมิดได้มาจากการเทน้ำใส่พีระมิด แล้วนำไปเทใส่ปริซึมหนึ่ง ซึ่งพื้นที่ฐานของพีระมิดจะต้องเท่ากับพื้นที่ฐานของปริซึม และความสูงของพีระมิดจะต้องเท่ากับความสูงของปริซึมนั้น โดยต้องเทน้ำจากพีระมิดใส่ลงในปริซึมนั้น 3 ครั้ง จึงจะได้น้ำเต็มปริซึมพอดี

เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กัน

ตัวอย่างที่ 2 พีระมิดฐานสี่เหลี่ยมผืนผ้าหนึ่ง มีฐานกว้างและยาวเป็น $5$ และ $6$ เซนติเมตร ตามลำดับ ถ้าพีระมิดนี้สูง $12$ เซนติเมตร แล้วปริมาตรของพีระมิดนี้เท่ากับเท่าใด

วิธีทำ จากสูตร ปริมาตรของพีระมิด $=\frac{1}{3}\times$ พื้นที่ฐาน $\times$ สูง
พื้นที่ฐาน $=5\times6=30$ ตารางเซนติเมตร
ดังนั้น ปริมาตรของพีระมิดนี้ คือ $\frac{1}{3}\times30\times12=120$ ลูกบาศก์เซนติเมตร

กรวยคืออะไร ?

สิ่งต่าง ๆ รอบตัวเราที่มีลักษณะเป็นแบบกรวยมีมากมาย และในทางคณิตศาสตร์นิยามความหมายของกรวยไว้ดังนี้

ในทางคณิตศาสตร์ รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน
และเส้นที่ต่อระหว่างจุดที่เป็นยอดแหลมและจุดใด ๆ บนของของฐานเป็นส่วนของเส้นตรง เรียกว่า กรวย (cone)

โดยเราจะเรียกส่วนประกอบของกรวยในแต่ละส่วน ดังรูปนี้

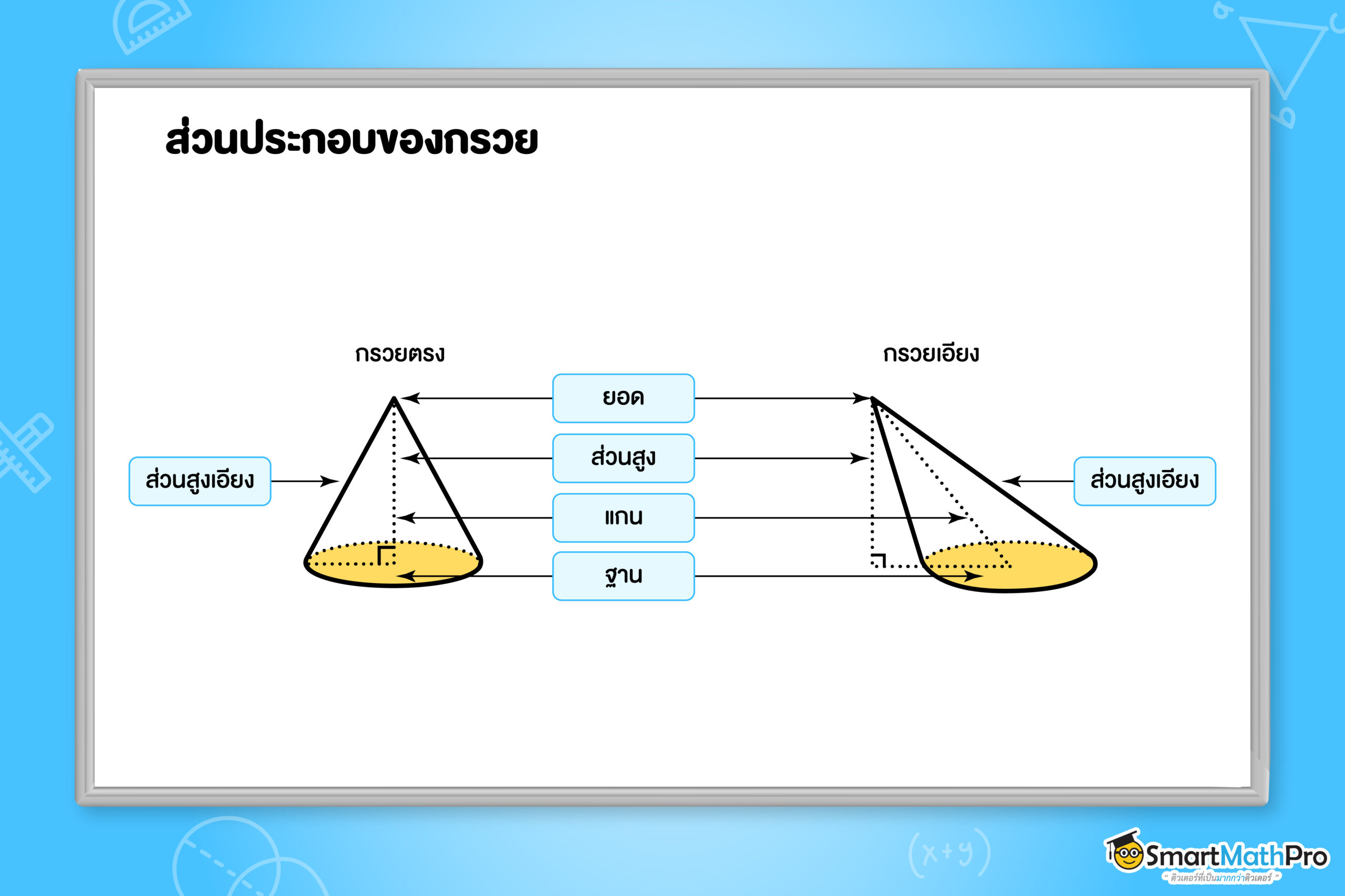
ในระดับชั้นนี้เราจะจะกล่าวถึงกรวยตรง (right cone) ที่อยู่ในรูปทางด้านซ้าย เป็นกรวยที่มีแกนตั้งฉากกับฐานที่จุดศูนย์กลางของฐานเท่านั้นน้า

พื้นที่ผิวของกรวย

ถ้าตัดกรวยออกตามแนวส่วนสูงเอียง แล้วคลี่ออก สังเกตได้ว่าพื้นที่ผิวของกรวยจะแบ่งออกเป็นสองส่วน ได้แก่ ส่วนที่เป็นวงกลม คือ พื้นที่ฐานของกรวย และส่วนที่คล้ายกับรูปสามเหลี่ยม คือ พื้นที่ผิวข้างของกรวย ดังรูปด้านล่าง

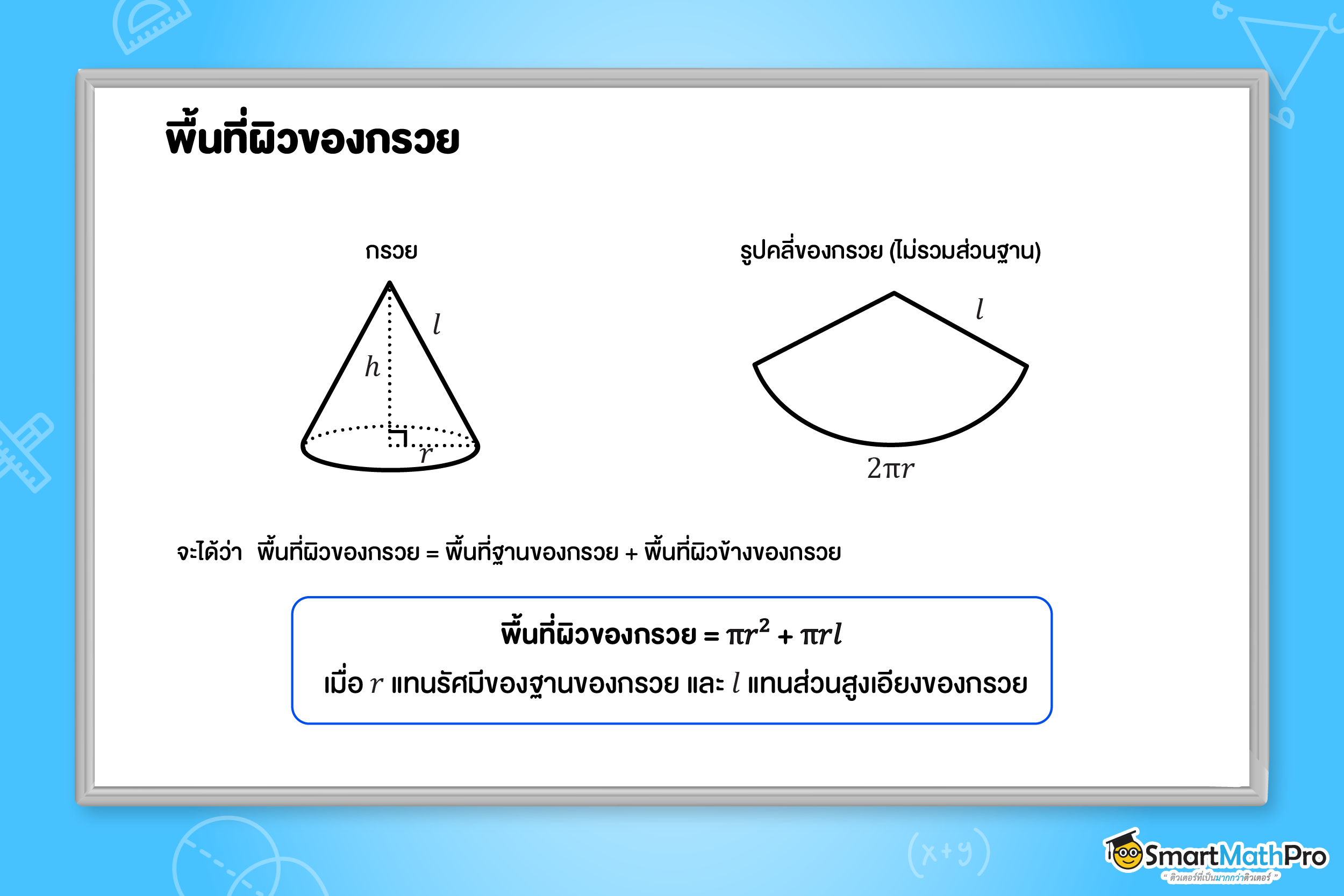
เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กัน

ตัวอย่างที่ 3 กรวยอันหนึ่งมีเส้นผ่านศูนย์กลางยาว $14$ เซนติเมตร และสูงเอียงยาว $10$ เซนติเมตร จงหาพื้นที่ผิวของกรวย (กำหนดให้ $\pi\approx \frac{22}{7}$ )

วิธีทำ จากโจทย์ กรวยมีเส้นผ่านศูนย์กลางยาว $14$ เซนติเมตร
จะได้ว่า กรวยจะมีรัศมียาว $\frac{14}{2}=7$ เซนติเมตร และสูงเอียงยาว $10$ เซนติเมตร
นั่นคือ กรวยนี้มี $r=7$ และ $l =10$
จากสูตรพื้นที่ผิวของกรวย $=\pi r^2+\pi rl$
เมื่อแทนค่าลงในสูตร จะได้ พื้นที่ผิวของกรวย ประมาณ $\left(\frac{22}{7}\times7\times7\right)+\left(\frac{22}{7}\times7\times10\right)\approx374$ ตารางเซนติเมตร

ปริมาตรของกรวย

จากที่ทราบความสัมพันธ์ระหว่างปริมาตรของพีระมิดและปริมาตรของปริซึมซึ่งมีพื้นที่ฐานเท่ากัน และส่วนสูงเท่ากันมาแล้ว ความสัมพันธ์ของปริมาตรของกรวยและทรงกระบอกก็เป็นไปในทำนองเดียวกัน

เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กัน

ตัวอย่างที่ 4 พี่บอสต้องการทำชาไทยแจกน้อง ๆ จำนวน $20$ คน โดยแต่ละคนจะใช้แก้วกรวยกระดาษที่มีรัศมี $4$ เซนติเมตร และสูง $6$ เซนติเมตร พี่บอสต้องทำชาไทยทั้งหมดประมาณกี่ลูกบาศก์เซนติเมตร (กำหนดให้ $\pi\approx 3.14$ )

วิธีทำ จากสูตร ปริมาตรของกรวย $=\frac{1}{3}\pi r^2h$
เมื่อแทนค่าลงในสูตร จะได้ว่า ปริมาตรของแก้วกรวยกระดาษ $\approx\frac{1}{3}\times3.14\times4^2\times6\approx100.48$ ลูกบาศก์เซนติเมตร
จากโจทย์ ต้องการแจกน้อง ๆ จำนวน $20$ คน
ดังนั้น พี่บอสต้องทำชาไทยทั้งหมดประมาณ $100.48\times20\approx2,009.6$ ลูกบาศก์เซนติเมตร

ทรงกลม

ทรงกลมเป็นรูปเรขาคณิตสามมิติซึ่งน้อง ๆ อาจจะพบเห็นได้บ่อยในชีวิตประจำวัน ทั้งพบได้จากสิ่งที่มนุษย์สร้างขึ้น และสิ่งที่มีอยู่ในธรรมชาติ หรือมีบางสิ่งที่มีลักษณะคล้ายทรงกลมด้วย เช่น ลูกบอล ส้ม ลูกโลก

ในทางคณิตศาสตร์ รูปเรขาคณิตสามมิติที่มีผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดคงที่จุดหนึ่ง
เป็นระยะเท่ากัน เรียกว่า ทรงกลม (sphere) จุดคงที่นั้นเรียกว่า จุดศูนย์กลางของทรงกลม
ระยะที่เท่ากันนั้นเรียกว่า รัศมีของทรงกลม

โดยเราจะเรียกส่วนประกอบของทรงกลมในแต่ละส่วน ดังรูปนี้

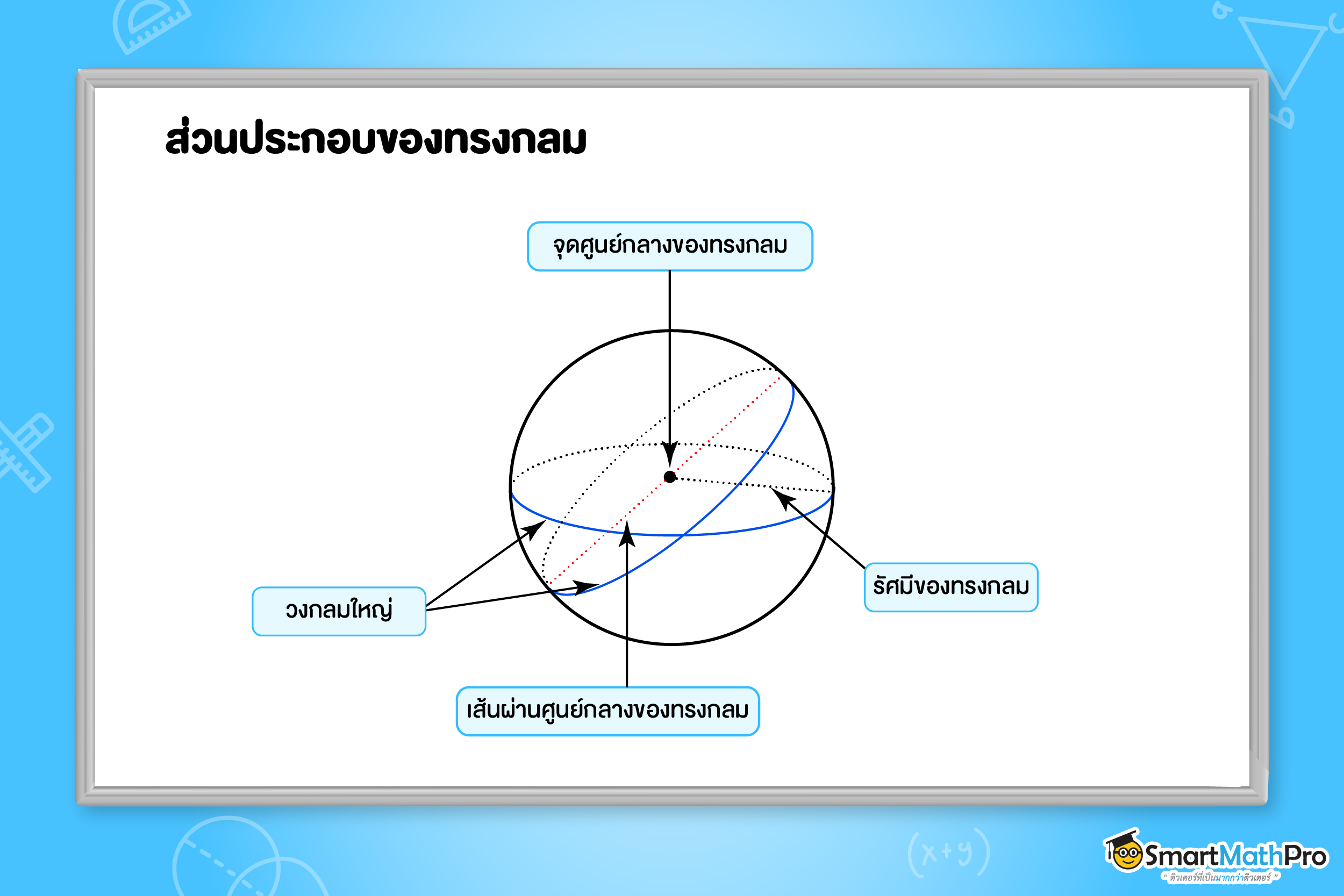
พื้นที่ผิวของทรงกลม

แนวคิดของการประมาณพื้นที่ผิวโค้งของทรงกลมจะทำได้โดยการแบ่งผิวโค้งออกเป็นรูปหลายเหลี่ยม เช่น ลูกฟุตบอลในภาพด้านล่างนี้เกิดจากการที่เรานำรูปห้าเหลี่ยมและหกเหลี่ยมมาประกอบกันเป็นทรงกลม หากเราหาพื้นที่ของรูปห้าเหลี่ยมและรูปหกเหลี่ยมย่อยเหล่านี้จะได้ นั่นหมายถึงว่าเราจะหาพื้นที่ผิวของทรงกลมได้

แต่เมื่อลองแกะรูปห้าเหลี่ยมและหกเหลี่ยมย่อยของลูกฟุตบอลออกมาจะพบว่ารูปห้าเหลี่ยมและหกเหลี่ยมนั้นยังมีพื้นผิวที่โค้ง ไม่แบนราบ นั่นหมายความว่าการหาพื้นที่ผิวของทรงกลมก็ยังค่อยไม่แม่นยำ

ถ้าเราต้องการให้หาพื้นที่ผิวของทรงกลมให้แม่นยำมากขึ้นจะต้องแบ่งพื้นที่ผิวของทรงกลมให้เป็นรูปหลายเหลี่ยมย่อยให้มากที่สุด ไม่ว่าจะเป็นพันรูป หมื่นรูปก็ตาม ยิ่งแบ่งย่อยได้เท่าไร การหาพื้นที่ผิวทรงกลมนี้ก็จะแม่นยำมากขึ้นเท่านั้น

โดยทั่วไปแล้วสูตรการหาพื้นที่ผิวของทรงกลมเป็นดังนี้

พื้นที่ผิวของทรงกลม $=4\pi{r}^{2}$
เมื่อ $r$ แทนรัศมีของทรงกลม

เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กัน

ตัวอย่างที่ 5 โนบิตะกำลังทำโคมไฟกระดาษรูปทรงกลมปิด โดยมีความยาวรอบทรงกลมนี้ $88$ เซนติเมตร (วัดจากบริเวณที่กว้างที่สุดของโคมไฟ) พื้นที่ผิวของโคมไฟนี้เท่ากับเท่าใด (กำหนดให้ $\pi\approx \frac{22}{7}$ )

วิธีทำ จากสูตร ความยาวเส้นรอบวง $=2\pi r$
จะได้ว่า $88=2\times\frac{22}{7}\times r$
นั่นคือ $r=14$

จากสูตร พื้นที่ผิวของทรงกลม $=4\pi r^2$

เมื่อแทนค่าลงในสูตร จะได้ว่า $4\times\frac{22}{7}\times{14}^2\approx2,464$
ดังนั้น พื้นที่ผิวของโคมไฟนี้ ประมาณ $2,464$ ตารางเซนติเมตร

ปริมาตรของทรงกลม

การหาปริมาตรรูปเรขาคณิตสามมิติก่อนหน้านี้ไม่ว่าจะเป็นพีระมิดหรือกรวย เราอาจใช้การเทน้ำ ซึ่งอาศัยความสัมพันธ์ระหว่างพีระมิดและปริซึม กรวยและทรงกระบอกมาแล้ว เพื่อให้ได้แนวคิดในการหาปริมาตรของทรงกลม เราจะพิจารณาปริมาตรของครึ่งทรงกลมและทรงกระบอก ดังนี้

ตัวอย่างที่ 6 ลูกชิ้นจัมโบ้ $9$ ลูก มีปริมาตรรวมกันเท่ากับ $1,617$ ลูกบาศก์เซนติเมตร แล้วความยาวของรัศมีของลูกชิ้นลูกหนึ่งเท่ากับกี่เซนติเมตร (กำหนดให้ $\pi\approx \frac{22}{7}$ )

วิธีทำ ลูกชิ้นจัมโบ้ $1$ ลูก จะมีปริมาตร $\frac{1,617\ }{9}$ ลูกบาศก์เซนติเมตร
จากสูตร ปริมาตรของทรงกลม $=\frac{4}{3}\pi r^3$
เมื่อแทนค่าลงในสูตร จะได้ $\frac{1,617\ }{9}\approx \frac{4}{3}\times\frac{22}{7}\times r^3$
จะได้ว่า $r^3\approx 42.875$
นั่นคือ $r\approx 3.5$
ดังนั้น ความยาวของรัศมีของลูกชิ้นลูกหนึ่ง ประมาณ $3.5$ เซนติเมตร

ตัวอย่างที่ 7 ถ้านำโลหะตันทรงกลมที่มีความยาวรัศมี $3$ เซนติเมตร จำนวน $4$ ลูก มาหลอมใหม่ทำเป็นโลหะตันทรงกรวยที่มีเส้นผ่านศูนย์กลางของฐานยาว $12$ เซนติเมตร แล้วโลหะตันทรงกรวยนี้จะสูงเท่ากับเท่าใด

วิธีทำ จากสูตร ปริมาตรของทรงกลม $=\frac{4}{3}\pi r^3$
จะได้ ปริมาตรโลหะตันทรงกลมมีความยาวรัศมี $3$ เซนติเมตร คือ $\frac{4}{3}\pi\left(3\right)^3=36\pi$ ลูกบาศก์เซนติเมตร
โลหะตันทรงกลม มีจำนวน $4$ ลูก จะมีปริมาตรทั้งหมด เท่ากับ $36\pi\times4=144\pi$ ลูกบาศก์เซนติเมตร
นำมาหลอมใหม่ทำเป็นโลหะตันทรงกรวยที่มีปริมาตรเท่ากัน คือ $144\pi$ ลูกบาศก์เซนติเมตร
จากโจทย์ โลหะตันทรงกรวย มีเส้นผ่านศูนย์กลางของฐานยาว $12$ เซนติเมตร นั่นคือ โลหะตันทรงกรวยจะมีรัศมี $\frac{12}{2}=6$ เซนติเมตร
จากสูตร ปริมาตรของกรวย $=\frac{1}{3}\pi r^2h$
เมื่อแทนค่าลงในสูตร จะได้ว่า $144\pi=\frac{1}{3}\pi\left(6\right)^2h$
$h=\frac{144\pi\times3}{36\pi}$
นั่นคือ $h=12$
ดังนั้น โลหะตันทรงกรวยนี้สูง $12$ เซนติเมตร

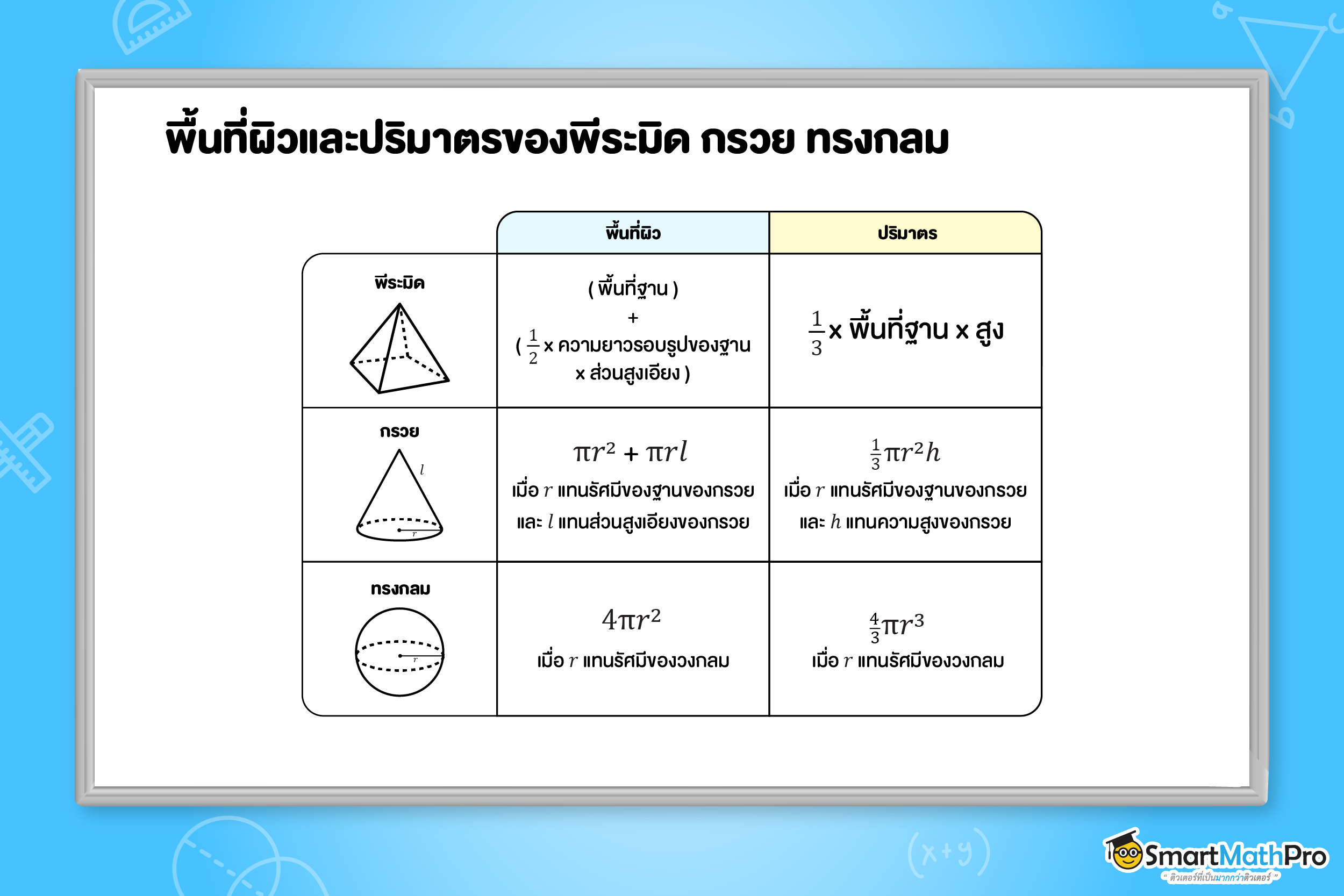
รวมสูตรพื้นที่ผิวและปริมาตร (พีระมิด กรวย ทรงกลม) ม.3

เราสามารถสรุปสูตรทั้งหมด 6 สูตรที่ได้เรียนมา ดังนี้

ติวคณิตศาสตร์ ม.ต้น กับ SmartMathPro

สำหรับน้อง ๆ ม.3 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์

พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.3 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก

อ่านกันมาจนถึงตรงนี้ พี่คิดว่าน้อง ๆ น่าจะเข้าใจเรื่องพีระมิด กรวย ทรงกลม ม.3 กันมากขึ้นแล้ว โดยพี่แนะนำให้ทำแบบฝึกหัดเรื่องนี้บ่อย ๆ เพราะจะช่วยให้แม่นยำในเนื้อหามากขึ้น ซึ่งนอกจากตัวอย่างโจทย์ให้ดูในบทความนี้แล้ว พี่ยังมี
แบบฝึกหัดให้ลองทำเพิ่มเติมด้วยน้าา