อยากรู้ว่ามีน้อง ๆ คนไหนรู้จักหรือคุ้น ๆ สัญลักษณ์ \sum กันบ้างง หลายคนอาจจะรู้อยู่แล้วว่ามันคือ ซิกมา (ซัมเมชัน) ซึ่งทุกคนจะได้เจอตอนเรียนคณิต ม.ปลาย
ซึ่งพี่เชื่อว่าน่าจะมีอีกหลายคนที่ยังไม่รู้จักสัญลักษณ์นี้และไม่รู้ว่ามันใช้เรียนในบทไหนใช่ไหม แต่ไม่ต้องกังวลน้า เพราะพี่มีสรุปเรื่องความหมาย พร้อมแจกสูตรและสมบัติของ ซิกมา (ซัมเมชัน) มาให้เรียบร้อยแล้ว ไปอ่านพร้อมกันได้เลยย > <
ซิกมา คือ สัญลักษณ์ที่ใช้ในการเขียนแสดงการบวกของจำนวนหรือพจน์ที่มีหลาย ๆ พจน์ต่อกัน หรือที่เรียกกันว่าอนุกรม ใช้เพื่อลดรูปการเขียนผลบวก (หรือผลรวม) แบบกระจายพจน์ ให้อยู่ภายใต้สัญลักษณ์ตัวนี้
ซึ่งผลบวกที่เขียนให้อยู่ในรูปซิกมาแล้ว เราจะเรียกว่า ซัมเมชัน (Summation) โดยน้อง ๆ จะได้เจอสัญลักษณ์นี้และได้ใช้ครั้งแรกในบท ลำดับและอนุกรม ในการพูดถึงผลบวกของลำดับ และจะได้ใช้อีกครั้งในบท สถิติ ที่จะต้องคำนวณผลบวกของค่าของตัวแปรต่าง ๆ
แนะนำสัญลักษณ์แสดงการบวก
การเขียนแสดงการบวกหลาย ๆ พจน์หรืออนุกรมนั้น เรามักจะใช้สัญลักษณ์จุดไข่ปลา 3 จุด \cdots ซึ่งลอยอยู่ระหว่างเครื่องหมายดำเนินการ (+, -) เพื่อละพจน์อื่น ๆ ไว้ในฐานที่เข้าใจ เช่น
1+2+3+\dots+100
หมายถึงการบวกกันของจำนวนนับทุกจำนวนตั้งแต่ 1 ถึง 100
แต่ว่าในบางครั้งรูปแบบของพจน์ที่เอามาบวกกันจะมีความซับซ้อน จึงไม่เหมาะกับการเขียนในลักษณะนี้ นักคณิตศาสตร์จึงคิดวิธีการเขียนแสดงการบวกโดยใช้สัญลักษณ์ “ซิกมา” ซึ่งเขียนแทนด้วย \sum (ตัวอักษรกรีกตัวพิมพ์ใหญ่) เพื่อความสะดวกในการเขียนอนุกรมต่าง ๆ มากขึ้น
ถ้าให้ a_n เป็นพจน์ที่ n ของลำดับ จะเขียนแทนอนุกรมจำกัด a_1+a_2+a_3+\dots+a_n ได้เป็น \sum_{i=1}^{n} a_i
โดยองค์ประกอบแต่ละอย่างมีความหมายดังต่อไปนี้
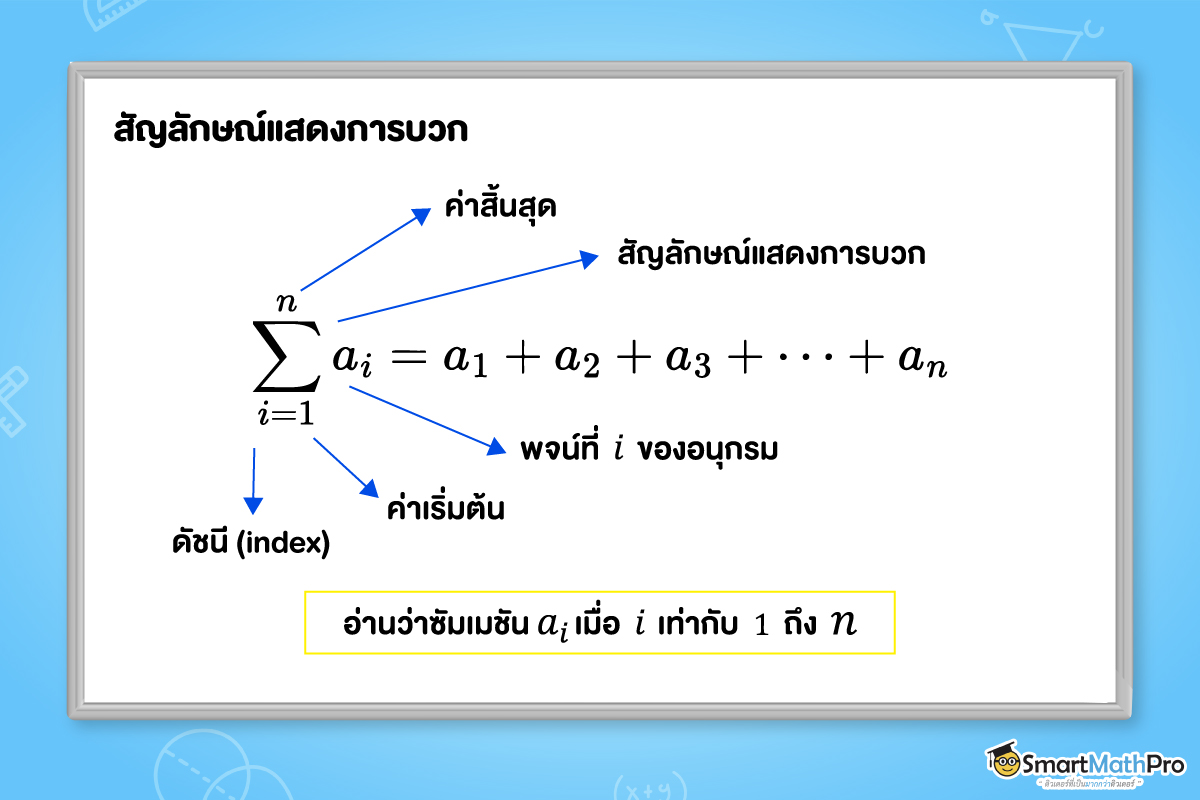
สำหรับอนุกรมอนันต์ a_1+a_2+a_3+\dots+a_{n}+\cdots จะเขียนในรูปซัมเมชันได้เป็น \sum_{i=1}^{\infty}a_i อ่านว่า ซัมเมชัน a_i เมื่อ i เท่ากับ 1 ถึง \infty (อินฟินิตี)
โดยทั่วไป การเขียนผลบวกในรูปซัมเมชัน สามารถใช้ตัวแปรเป็นตัวอักษรอื่น และดัชนีไม่จำเป็นต้องเริ่มต้นที่ 1 เสมอไป
ตัวอย่างที่ 1 จงเขียนแทนสัญลักษณ์ต่อไปนี้ให้อยู่ในรูปการบวก
- \sum_{i=1}^{6} i
วิธีทำ \sum_{i=1}^{6} i=1+2+3+4+5+6 - \sum_{i=1}^{4} \left(i^2-i \right)
วิธีทำ \sum_{i=1}^{4} \left(i^2-i \right)=\left(1^2-1 \right)+\left(2^2-2 \right)+\left(3^2-3 \right)+\left(4^2-4 \right) - \sum_{i=1}^{\infty} \frac{5}{2^i}
วิธีทำ \sum_{i=1}^{\infty}\frac{5}{2^i}=\frac{5}{2^1}+\frac{5}{2^2}+\frac{5}{2^3}+\cdots+\frac{5}{2^n}+\cdots
ตัวอย่างที่ 2 จงเขียนอนุกรมต่อไปนี้โดยใช้สัญลักษณ์ \sum
- 1+2+3+\dots+100
วิธีทำ 1+2+3+\dots+100=\sum_{i=1}^{100} i - \left(1^3+2\right)+\left(2^3+2\right)+\left(3^3+2\right)+\left(4^3+2\right)+\left(5^3+2\right)
วิธีทำ \left(1^3+2\right)+\left(2^3+2\right)+\left(3^3+2\right)+\left(4^3+2\right)+\left(5^3+2\right)=\sum_{i=1}^{5}\left(i^3+2\right) - 1\cdot4+2\cdot5+3\cdot6+4\cdot7+\cdots
วิธีทำ
พจน์ที่ 1 มีตัวคูณ 2 ตัว คือ 1 และ 4
ซึ่ง 4=1+3
พจน์ที่ 2 มีตัวคูณ 2 ตัว คือ 2 และ 5
ซึ่ง 5=2+3
พจน์ที่ 3 มีตัวคูณ 2 ตัว คือ 3 และ 6
ซึ่ง 6=3+3
แสดงว่าพจน์ที่ i มีตัวคูณ 2 ตัว คือ i และ i+3
จะได้ 1\cdot4+2\cdot5+3\cdot6+4\cdot7+\cdots=\sum_{i=1}^{\infty} i\left(i+3\right)
สมบัติของซิกมา (ซัมเมชัน)
เช่น
- \sum_{i=1}^{12} 3=12\left(3\right)=36
- \sum_{i=1}^{20} 4i=4\sum_{i=1}^{20} i
- \sum_{i=1}^{40} \left(i^2+i\right)=\sum_{i=1}^{40} i^2+\sum_{i=1}^{40}i
- \sum_{i=1}^{40} \left(i^2-i\right)=\sum_{i=1}^{40} i^2-\sum_{i=1}^{40}i
สูตรเกี่ยวกับซิกมา (ซัมเมชัน)
สูตรของผลบวกอนุกรมที่น่าสนใจและใช้เป็นประจำ มีอยู่ 3 สูตรด้วยกัน คือ สูตรของ
\sum_{i=1}^{n}i\space,\sum_{i=1}^{n}i^2 และ \sum_{i=1}^{n}i^3 เมื่อ n เป็นจำนวนนับ จะได้ผลลัพธ์ตามนี้เลย
เช่น
- \sum_{i=1}^{12}i=\frac{12\left(12+1\right)}{2}=78
- \sum_{i=1}^{7}i^2=\frac{\left(7\right)\left(7+1\right)\left[2\left(7\right)+1\right]}{6}=140
- \sum_{i=1}^{5}i^3=\left[\frac{\left(5\right)\left(5+1\right)}{2}\right]^2=225
ด้วยสูตรเหล่านี้ จะทำให้เราสามารถลดระยะเวลาในการคำนวณหาผลบวกที่มีจำนวนพจน์เยอะ ๆ ได้โดยไม่ต้องเสียเวลาคิดทีละพจน์บวกกัน
แบบฝึกหัดซิกมา (ซัมเมชัน) พร้อมเฉลย
ตัวอย่างที่ 3 จงหาค่าของ \sum_{i=1}^{20}\left(2i+3\right)
วิธีทำ
\sum_{i=1}^{20}\left(2i+3\right) =\sum_{i=1}^{20} 2i + \sum_{i=1}^{20} 3\\
=2\sum_{i=1}^{20} i + 3\left(20\right)\\
=2\cdot\frac{\left(20\right)\left(20+1\right)}{{2}} + 60\\
=420 + 60\\
=480
ตัวอย่างที่ 4 จงหาค่าของ \sum_{i=1}^{8}\left(i^3-i^2\right)
วิธีทำ
\sum_{i=1}^{8}\left(i^3-i^2\right) =\sum_{i=1}^{8}i^3-\sum_{i=1}^{8}i^2\\
=\left[\frac{\left(8\right)\left(8+1\right)}{2}\right]^2-
\frac{\left(8\right)\left(8+1\right)\left[2\left(8\right)+1\right]}{6}\\
=\left[\frac{\left(8\right)\left(9\right)}{2}\right]^2-
\frac{\left(8\right)\left(9\right)\left(17\right)}{6}\\
=36^2-204\\
=1,296-204\\
=1,092\\
ตัวอย่างที่ 5 จงหาค่าของ \sum_{k=1}^{10}\left(k-7\right)\left(k+2\right)
แนวคิด ถ้าภายในซิกมา มีพจน์ตั้งแต่ 2 พจน์ขึ้นไปคูณกัน เราจะไม่สามารถกระจายซิกมาเข้าไปในแต่ละพจน์ได้ ต้องจับแต่ละพจน์คูณกันให้เรียบร้อยก่อนจึงจะกระจายได้
วิธีทำ
\sum_{k=1}^{10}\left(k-7\right)\left(k+2\right)=\sum_{k=1}^{10}\left(k^2-5k-14\right)\\
=\sum_{k=1}^{10}k^2-\sum_{k=1}^{10}5k-\sum_{k=1}^{10}14\\
=\sum_{k=1}^{10}k^2-5\sum_{k=1}^{10}k-\sum_{k=1}^{10}14\\
=\frac{\left(10\right)\left(10+1\right)\left[2\left(10\right)+1\right]}{6}-
5\cdot\frac{\left(10\right)\left(10+1\right)}{2}-14\left(10\right)\\
=\frac{\left(10\right)\left(11\right)\left(21\right)}{6}-5\cdot\frac{\left(10\right)\left(11\right)}{2}-140\\
=385-275-140\\
=-30\\
ดูคลิปติว "ซิกมา" (ซัมเมชัน)
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
พี่เชื่อว่าทุกคนน่าจะรู้จักเกี่ยวกับ “ซิกมา” แบบเบื้องต้นกันไปประมาณหนึ่งแล้ว และหวังว่าจะนำไปประยุกต์กับเนื้อหาลำดับและอนุกรม รวมถึงบทอื่น ๆ ที่เกี่ยวข้องได้น้าา อย่างไรก็ตามถ้าอยากจะเก่งคณิตมากขึ้น พี่แนะนำว่าให้ทบทวนเนื้อหาและควรฝึกทำโจทย์บ่อย ๆ ด้วยย
หรือถ้าน้อง ๆ รู้สึกว่าเนื้อหาคณิตศาสตร์ ม.ปลายดูเป็นเรื่องยาก กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากเสริมพื้นฐานให้แน่นและอยากได้คนช่วยไกด์ พี่ก็ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย !!
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
เลขยกกำลัง คืออะไร? สรุปเนื้อหาพร้อมแจกตารางเลขยกกำลังที่ควรรู้
ลำดับและอนุกรม ม.6 คืออะไร สรุปเนื้อหาพร้อมตัวอย่างโจทย์และวิธีทำ
สถิติ ม.6 สรุปเนื้อหาสถิติและข้อมูล พร้อมโจทย์แบบจัดเต็ม ! – SmartMathPro
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
