น้อง ๆ รู้กันไหมว่าทฤษฎีบทพีทาโกรัส ม.2 เป็นเนื้อหาที่นำไปต่อยอดได้ทั้งคณิต ม.ต้นและคณิต ม.ปลาย ดังนั้นการเก็บเนื้อหาของทฤษฎีบทพีทาโกรัสให้แม่นก็จะช่วยให้น้อง ๆ เข้าใจเนื้อหาคณิตศาสตร์เรื่องอื่นได้อีกมากเลยน้า
แต่ใครที่ยังไม่แม่นก็ไม่ต้องกังวลไปเพราะว่าพี่เตรียมสรุปเนื้อหาของบทเรียนมาให้แบบจัดเต็มแล้ว แถมยังมีตัวอย่างโจทย์และแบบฝึกหัดให้ลองทำท้ายบทความอีกด้วยย
ทฤษฎีบทพีทาโกรัส (Pythagoras’ theorem) คือ ทฤษฎีหรือสมบัติที่เกี่ยวกับความยาวด้านของรูปสามเหลี่ยมมุมฉาก น้อง ๆ จะได้เรียนในระดับชั้น ม.2 เทอม 1 ซึ่งสามารถนำไปใช้แก้โจทย์ปัญหาหรือพิสูจน์ทฤษฎีหรือสมบัติอื่น ๆ ในบทที่เกี่ยวกับเรขาคณิตได้
เช่น บทปริซึมและทรงกระบอก ที่จะเจอในบทถัดไป รวมไปถึงบทพีระมิด กรวย ทรงกลม และ บทอัตราส่วนตรีโกณมิติ ในระดับชั้น ม.3 นอกจากนี้ยังต่อยอดไปเป็นพื้นฐานของเนื้อหาคณิตศาสตร์ ม.ปลายหลายบท และนำไปใช้ในวิชาวิทยาศาสตร์ได้อีกด้วย
แต่ก่อนจะไปเข้าเรื่องทฤษฎีบท เรามารู้จักชื่อเรียกแต่ละด้านของรูปสามเหลี่ยมมุมฉากกันก่อนน้าา
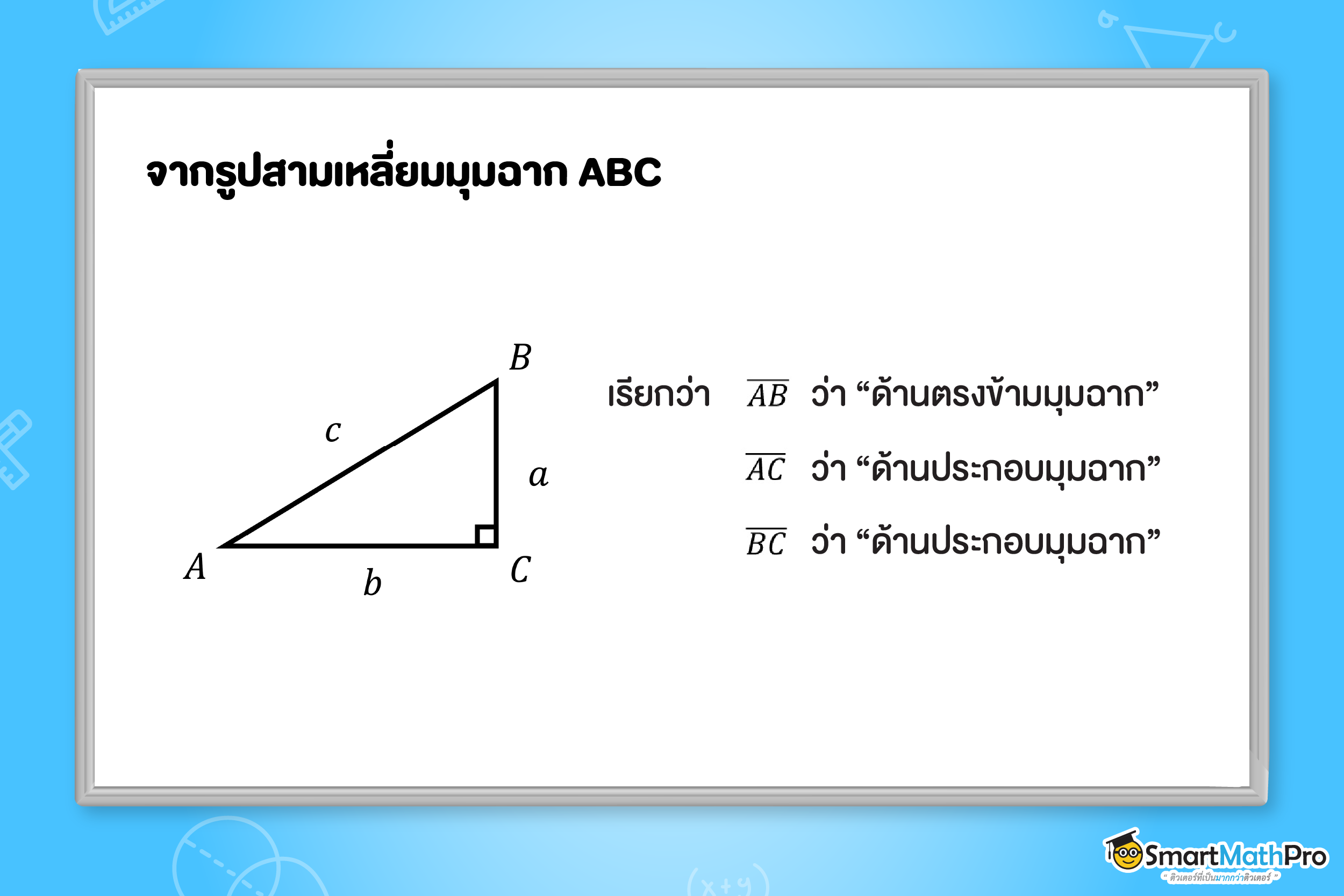
หมายเหตุ : ด้านตรงข้ามมุมฉากคือด้านที่มีความยาวมากที่สุดเสมอ
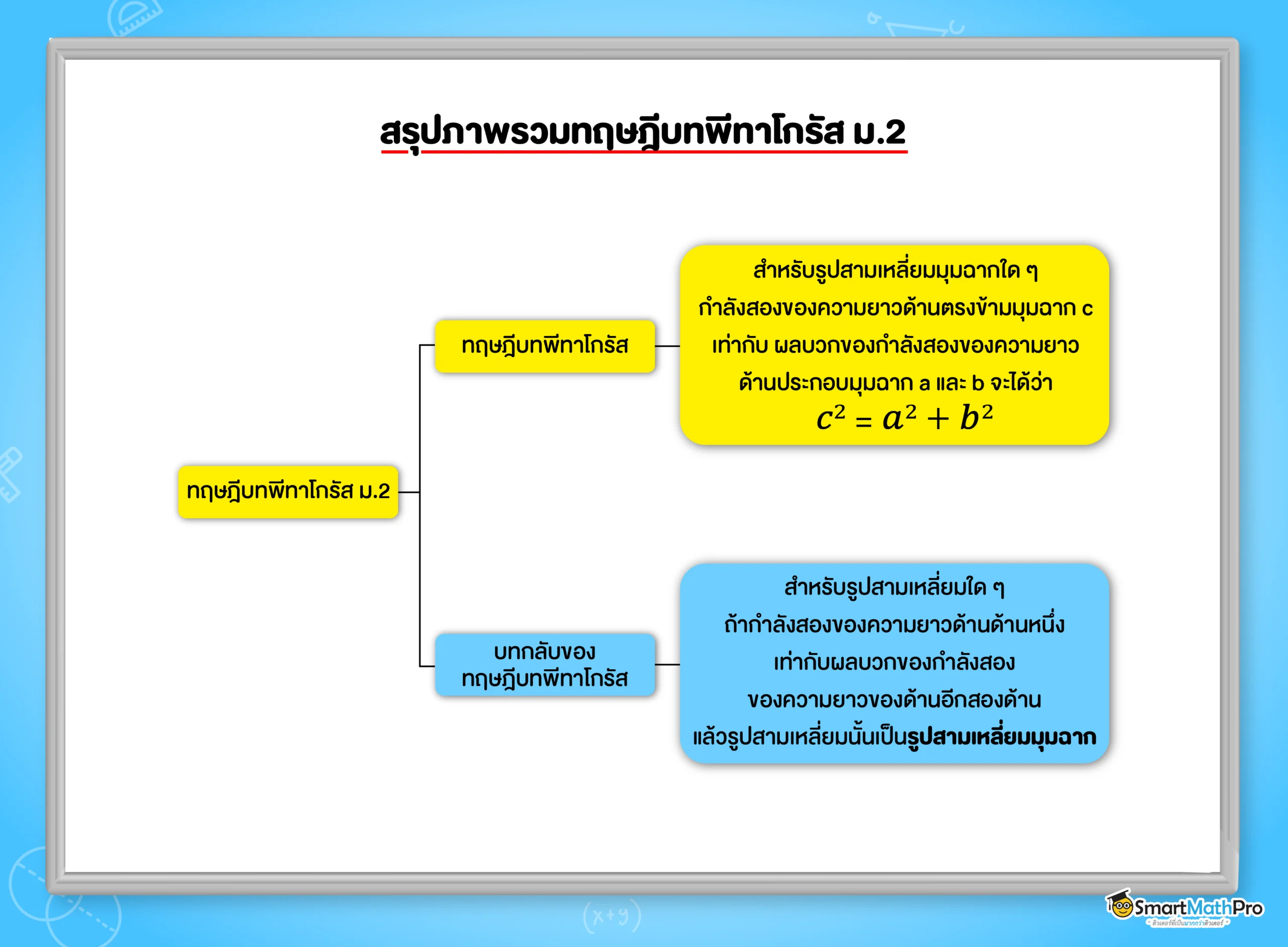
ทฤษฎีบทพีทาโกรัส
เป็นทฤษฎีที่กล่าวถึงความสัมพันธ์ระหว่างความยาวของด้านทั้งสามของรูปสามเหลี่ยมมุมฉาก ซึ่งในทางทฤษฎีได้บอกเอาไว้ว่า
ทฤษฎีบทพีทาโกรัส (Pythagoras’ theorem)
สำหรับรูปสามเหลี่ยมมุมฉากใด ๆ กำลังสองของความยาวของด้านตรงข้ามมุมฉาก
เท่ากับผลบวกของกำลังสองของความยาวของด้านประกอบมุมฉาก
จากทฤษฎีบทข้างต้นสามารถสรุปได้ว่า
ตัวอย่างที่ 1 จากรูปสามเหลี่ยมที่กำหนดให้ จงหาค่าของ x
วิธีทำ
เนื่องจาก x เป็นความยาวของด้านตรงข้ามมุมฉาก
และ 3, 4 เป็นความยาวของด้านประกอบมุมฉาก
จากทฤษฎีบทพีทาโกรัส จะได้ว่า x^{2}=3^{2}+4^{2}\\= 9+16\\=25
แสดงว่า x=-5, 5
ดังนั้น x=5
หมายเหตุ : สมการ x^{2}=25 มี 2 คำตอบคือ x=5 และ x=-5 แต่เนื่องจาก x เป็นความยาวของด้านตรงข้ามมุมฉาก ค่า x ที่เป็นจำนวนลบจึงใช้ไม่ได้น้าา
ตัวอย่างที่ 2 จากรูปสามเหลี่ยมที่กำหนดให้ จงหาค่าของ x
วิธีทำ
เนื่องจาก 13 เป็นความยาวของด้านตรงข้ามมุมฉาก
และ x, 12 เป็นความยาวของด้านประกอบมุมฉาก
จากทฤษฎีบทพีทาโกรัส จะได้ว่า 13^{2}=x^{2}+5^{2}\\x^{2}=13^{2}-5^{2}\\=169-25\\=144
ดังนั้น x=12
ตัวอย่างที่ 3 จากรูปสามเหลี่ยมที่กำหนดให้ จงหาพื้นที่ของรูปสามเหลี่ยม ABC
วิธีทำ
เนื่องจาก AB เป็นความยาวของด้านตรงข้ามมุมฉาก
และ AC, BC เป็นความยาวของด้านประกอบมุมฉาก
จากทฤษฎีบทพีทาโกรัส จะได้ว่า 25^{2}=BC^{2}+7^{2}\\BC^{2}=25^{2}-7^{2}\\=625-49\\=576\\BC=24
เราสามารถหาพื้นที่ของรูปสามเหลี่ยม ABC ได้จากสูตร \frac{1}{2}\times AC\times BC
จะได้ =\frac{1}{2}\times 7\times 24\\=84
ดังนั้น พื้นที่ของรูปสามเหลี่ยม ABC เท่ากับ 84 ตารางหน่วย
หลังจากที่น้อง ๆ ได้เรียนทฤษฎีบทพีทาโกรัสไปแล้ว จะสังเกตเห็นว่ามีเลขชุดพีทาโกรัสที่เราเจอบ่อย ๆ
ซึ่งเป็นชุดตัวเลขที่ได้จากการคำนวณตามทฤษฎีบท ซึ่งถ้าน้อง ๆ จำเลขชุดนี้ได้ จะทำให้เราแก้โจทย์ได้เร็วขึ้นด้วยนะ โดยเลขชุดพีทาโกรัสที่เจอบ่อยและนิยมใช้กันมีดังนี้
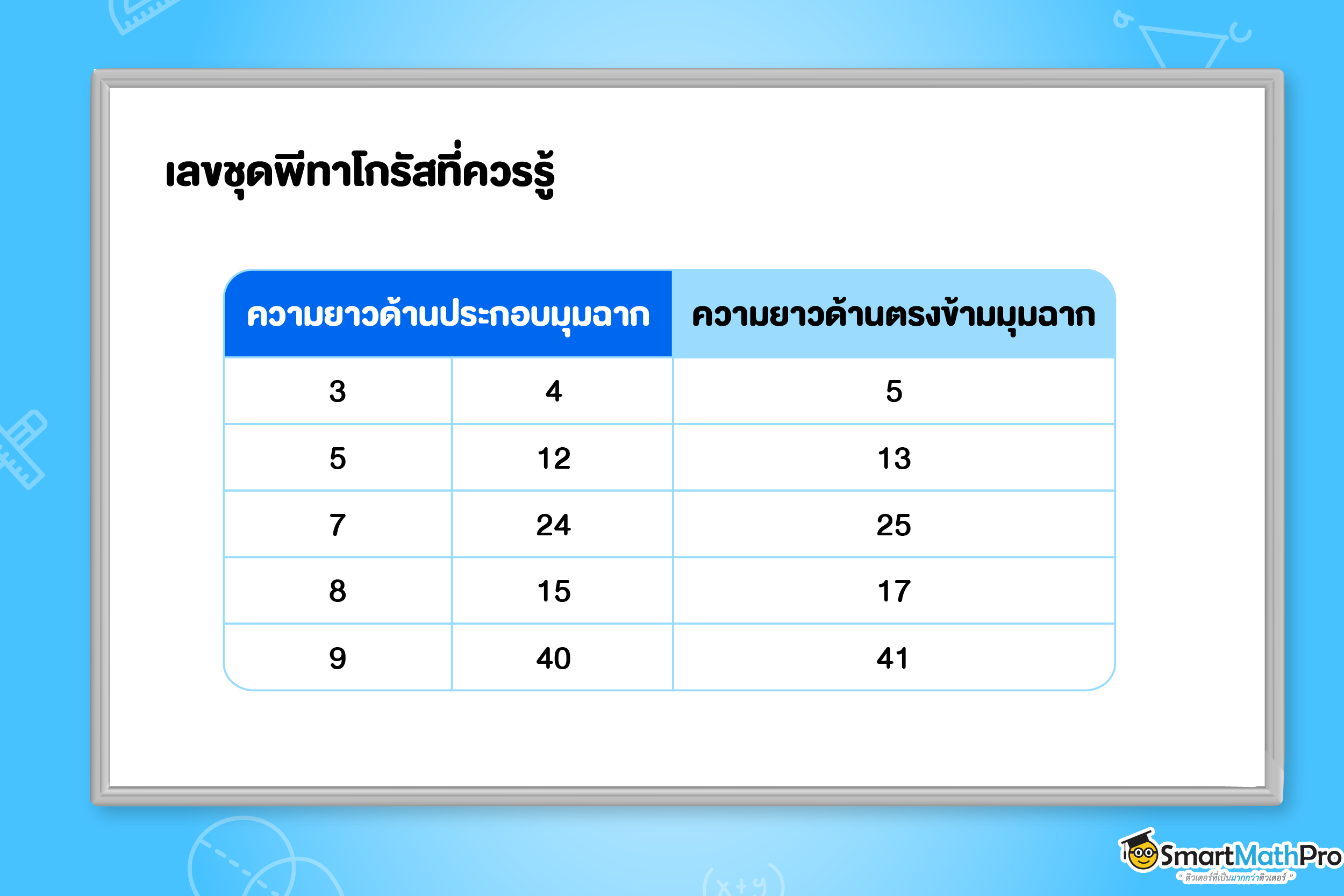
เลขชุดพีทาโกรัสจะใช้เมื่อรู้ความยาวด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉากจะสามารถหาความยาวอีกด้านหนึ่งได้ เช่น
- รูปสามเหลี่ยมมุมฉากที่มีความยาวด้านคือ 3, 4, x โดยที่ x เป็นความยาวด้านตรงข้ามมุมฉาก
แสดงว่า เลขชุดพีทาโกรัสที่ใช้ได้ก็คือชุด 3, 4, 5
ดังนั้น x=5
นอกจากเลขชุดพีทาโกรัสที่ควรรู้แล้ว ยังมีเลขชุดที่เกิดจากการประยุกต์ความรู้โดยดูความสัมพันธ์จากเลขชุดพีทาโกรัส เช่น
- รูปสามเหลี่ยมมุมฉากที่มีความยาวด้านคือ 6, 8, x โดยที่ x เป็นความยาวด้านตรงข้ามมุมฉาก
แสดงว่า x^{2}=6^{2}+8^{2}\\=36+64\\=100\\x=10
จะได้เลขชุดพีทาโกรัสชุดใหม่คือ 6, 8, 10
ซึ่งเมื่อสังเกตความสัมพันธ์จะเห็นว่า 6, 8, 10 เกิดจาก 3\times 2, 4\times 2, 5\times 2
ดังนั้น เลขชุดพีทาโกรัสชุดใหม่นี้ เกิดจากความสัมพันธ์ของเลขชุด 3, 4, 5 นำไปคูณด้วยสองในทุกด้านนั่นเอง
หมายเหตุ : การประยุกต์ความรู้โดยดูความสัมพันธ์จากเลขชุดพีทาโกรัส จะต้องเป็นการนำเลขชุดพีทาโกรัสไปคูณหรือหารด้วยจำนวนเดียวกันเท่านั้น
ข้อระวัง ต้องตรวจสอบว่าความยาวด้านที่นำมาพิจารณา เป็นความยาวด้านของด้านประกอบมุมฉากหรือด้านตรงข้ามมุมฉากด้วยนะ เพราะเลขชุดพีทาโกรัส จะต้องอยู่ในด้านที่ถูกต้องถึงจะใช้ได้น้า
ตัวอย่างที่ 4 จากรูปสามเหลี่ยมที่กำหนดให้ จงหาค่าของ x
วิธีทำ
จากโจทย์ จะได้ว่า รูปสามเหลี่ยมนี้มีความยาวด้านคือ 9, x, 15 โดยที่ x เป็นความยาวของด้านประกอบมุมฉาก
เมื่อเรานำเลขชุดพีทาโกรัส 3, 4, 5 ไปคูณด้วยสาม
ผลลัพธ์คือ 3\times 3, 4\times 3, 5\times 3
จะได้เลขชุดพีทาโกรัส 9, 12, 15 ซึ่งตรงกับความยาวด้านของรูปสามเหลี่ยมมุมฉากนี้
ดังนั้น x=12
บทกลับของทฤษฎีบทพีทาโกรัส
จากเนื้อหาของบทความที่ผ่านมา น้อง ๆ จะรู้ว่าถ้ามีรูปสามเหลี่ยมมุมฉากแล้วความยาวด้านจะมีความสัมพันธ์ตามทฤษฎีบทพีทาโกรัส ในทางกลับกัน ถ้านำความยาวด้านของรูปสามเหลี่ยมที่สอดคล้องกับทฤษฎีบทพีทาโกรัสมาพิจารณาก็จะสามารถสรุปได้ว่ารูปสามเหลี่ยมที่พิจารณาอยู่เป็นรูปสามเหลี่ยมมุมฉากหรือไม่เป็นรูปสามเหลี่ยมมุมฉากได้เช่นกัน
บทกลับของทฤษฎีบทพีทาโกรัส (converse of Pythagoras’ theorem)
สำหรับรูปสามเหลี่ยมใด ๆ ถ้ากำลังสองของความยาวของด้านด้านหนึ่ง
เท่ากับผลบวกของกำลังสองของความยาวของด้านอีกสองด้าน แล้วรูปสามเหลี่ยมนั้นเป็นรูปสามเหลี่ยมมุมฉาก
จากทฤษฎีบทข้างต้นสามารถสรุปได้ว่า
ตัวอย่างที่ 5 กำหนดให้ 10, 24 และ 26 เป็นความยาวของด้านของรูปสามเหลี่ยม จงพิจารณาว่าเป็นรูปสามเหลี่ยมมุมฉากหรือไม่
วิธีทำ จากความยาวด้านที่กำหนดให้ ถ้าสามเหลี่ยมรูปนี้เป็นสามเหลี่ยมมุมฉาก ด้านที่ยาวที่สุดจะเป็นด้านตรงข้ามมุมฉากเสมอ นั่นก็คือ 26
ให้ a=10, b=24 และ c=26
จะได้ a^{2}=100, b^{2}=576 และ c^{2}=676
ซึ่ง 676=100+576\\676=676
แสดงว่า c^{2}=a^{2}+b^{2}
โดยบทกลับของทฤษฎีบทพีทาโกรัส สรุปได้ว่า รูปสามเหลี่ยมที่มีความยาวด้าน คือ 10, 24, 26 เป็นรูปสามเหลี่ยมมุมฉาก
เทคนิค ! สามารถใช้เลขชุดพีทาโกรัสมาช่วยได้ด้วยน้า
จากโจทย์ 10, 24, 26 เกิดจาก 5\times 2, 12\times 2, 13\times 2
แสดงว่า ความยาวด้านของสามเหลี่ยมรูปนี้ เกิดจากเลขชุดพีทาโกรัส คือ 5, 12, 13
ดังนั้น รูปสามเหลี่ยมนี้เป็นรูปสามเหลี่ยมมุมฉากแน่นอน
ข้อระวัง ตัวเลขที่อยู่นอกเหนือเลขชุดพีทาโกรัสที่กำหนดให้ จะไม่สามารถบอกได้แน่ชัดนะว่าเป็นรูปสามเหลี่ยมมุมฉากหรือไม่ (ถึงจะไม่ได้เป็นเลขชุดพีทาโกรัสที่เรารู้จัก แต่อาจเป็นรูปสามเหลี่ยมมุมฉากก็ได้น้า)
ตัวอย่างที่ 6 กำหนดให้ 4, 6 และ 8 เป็นความยาวของด้านของรูปสามเหลี่ยม จงพิจารณาว่าเป็นรูปสามเหลี่ยมมุมฉากหรือไม่
วิธีทำ จากความยาวด้านที่กำหนดให้ ถ้าสามเหลี่ยมรูปนี้เป็นสามเหลี่ยมมุมฉาก ด้านที่ยาวที่สุดจะเป็นด้านตรงข้ามมุมฉากเสมอ นั่นก็คือ 8
ให้ a=4, b=6 และ c=8
จะได้ a^{2}=16, b^{2}=36 และ c^{2}=64
ซึ่ง 64\neq 16+36\\64\neq 52
แสดงว่า c^{2}\neq a^{2}+b^{2}
โดยบทกลับของทฤษฎีบทพีทาโกรัส สรุปได้ว่า รูปสามเหลี่ยมที่มีความยาวด้าน คือ 4, 6, 8 ไม่เป็นรูปสามเหลี่ยมมุมฉาก
โจทย์ปัญหาทฤษฎีบทพีทาโกรัส
เราสามารถนำความรู้ทฤษฎีบทพีทาโกรัสมาประยุกต์เพื่อแก้โจทย์ปัญหาได้ดังนี้
ตัวอย่างที่ 7 ชายหนุ่มคนหนึ่งต้องการนำบันไดพาดกับผนังกำแพงด้านหนึ่ง ถ้าปลายบันไดที่อยู่บนพื้นดินห่างจากผนังกำแพง 6 เมตร และผนังกำแพงสูง 2.5 เมตร ชายหนุ่มต้องใช้บันไดยาวกี่เมตร เพื่อให้ปลายบันไดอีกข้างหนึ่งแตะขอบบนของผนังกำแพงพอดี
วิธีทำ จากรูปจะสังเกตได้ว่า ระยะห่างจากปลายบันไดบนพื้นดินกับผนังกำแพง และความสูงของผนังกำแพง เป็นความยาวของด้านประกอบมุมฉาก และความยาวของบันไดเป็นความยาวของด้านตรงข้ามมุมฉาก
ให้ a=6, b=2.5 และ c=x
จากทฤษฎีบทพีทาโกรัส จะได้ว่า x^{2}=6^{2}+2.5^{2}\\=36+6.25\\=42.25
ดังนั้น x=6.5 เมตร
นั่นคือ ชายหนุ่มต้องใช้บันไดยาว 6.5 เมตร เพื่อให้ปลายบันไดอีกข้างหนึ่งแตะขอบบนของผนังกำแพงพอดี
เทคนิค ! เรายังสามารถใช้เลขชุดพีทาโกรัสได้อีกด้วย
เมื่อสังเกตความสัมพันธ์จะเห็นว่า 2.5, 6, x เกิดจาก \frac{5}{2}, \frac{12}{2}, \frac{13}{2}
ซึ่งเป็นการประยุกต์ใช้เลขชุดพีทาโกรัส 5, 12, 13 ไปหารด้วยสองในความยาวของทุกด้านนั่นเอง
เราก็จะได้ x=\frac{13}{2}\\=6.5 เช่นกัน
สำหรับใครที่อยากแม่นเนื้อหาทฤษฎีบทพีทาโกรัส ม.2 พี่แนะนำว่าควรทบทวนเนื้อหาอย่างสม่ำเสมอและลองฝึกทำ
แบบฝึกหัดเพิ่มเติมด้วยน้า และน้อง ๆ ม.2 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์
พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.2 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน แนวข้อสอบเข้าม.4 และข้อสอบแข่งขัน ถ้าใครสนใจดู
รายละเอียดเพิ่มเติม คลิก เลย
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุปเนื้อหา เส้นขนาน ม.2 พร้อมแจกโจทย์ให้ฝึกทำ
การแยกตัวประกอบของพหุนามดีกรีสอง ม.2 สรุปเนื้อหาและสูตรครบ
สรุป แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 พร้อมโจทย์+เฉลย
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
