สรุปเนื้อหาจำนวนจริง ม.2 พร้อมโจทย์และเฉลยฟรี

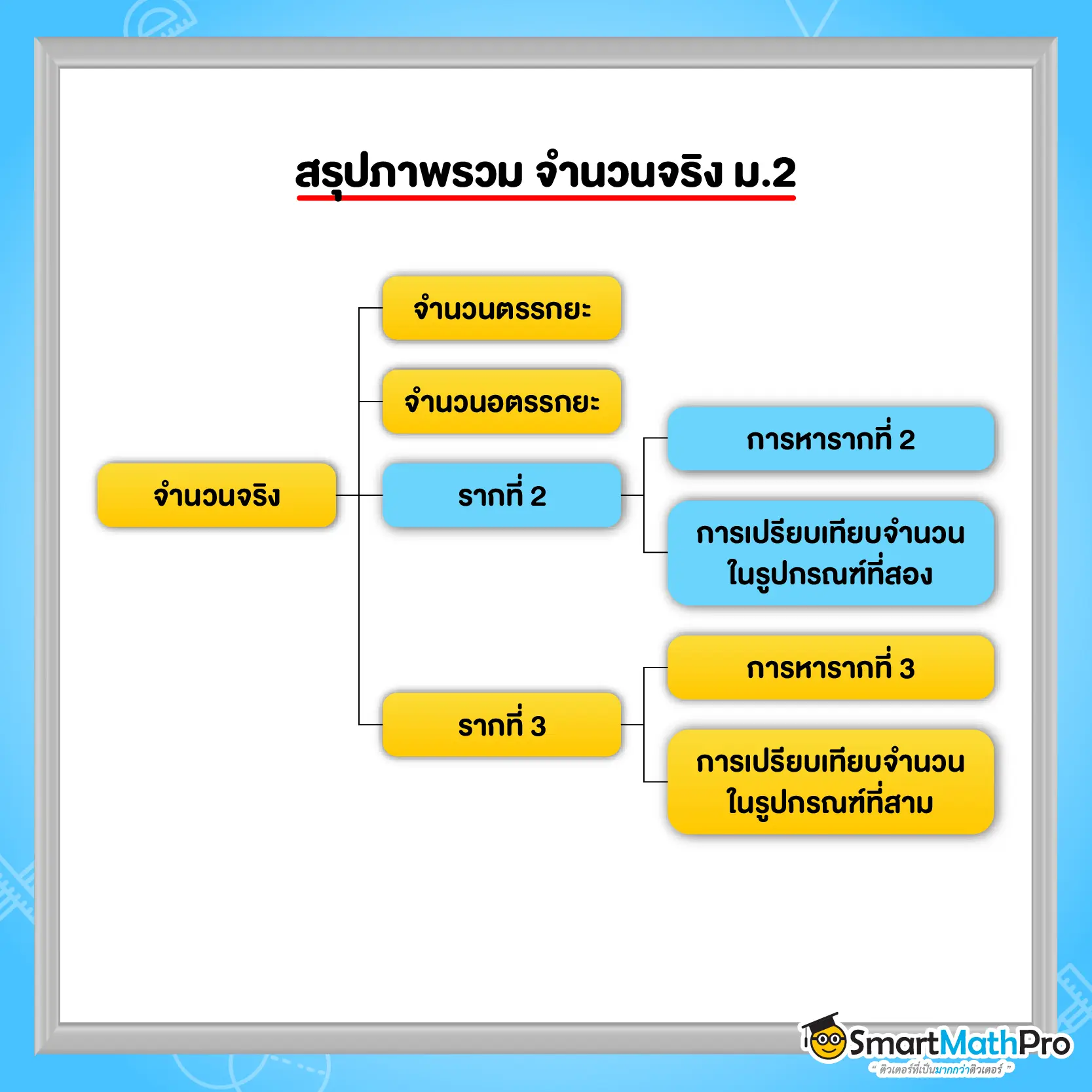
น้อง ๆ คนไหนที่ต้องการสรุปเนื้อหาจำนวนจริง ม.2 เพื่อไปใช้เตรียมสอบ สามารถดูจากบทความนี้ได้เลยน้าา เพราะพี่ทำสรุปมาให้ครบ ทั้งเรื่องความหมายของจำนวนจริง, จำนวนตรรกยะ, จำนวนอตรรกยะ, รากที่สอง, รากที่สาม พร้อมแจกแบบฝึกหัด+เฉลยให้น้อง ๆ ได้ลองทำกันท้ายบทความด้วยยย

สนใจหัวข้อไหน ... กดอ่านเลย

ภาพรวมจำนวนจริง ม.2

จำนวนจริงคืออะไร ?

ในทางคณิตศาสตร์ จำนวนจริงคือจำนวนที่สามารถเขียนแทนด้วยจุดบนเส้นจำนวนได้ และจุดใด ๆ แต่ละจุดบนเส้นจำนวนจะแทนจำนวนจริงจำนวนหนึ่ง ซึ่งอาจเป็นจำนวนตรรกยะหรือจำนวนอตรรกยะก็ได้ ดังนั้นเราจึงเรียกเส้นจำนวนนั้นว่า เส้นจำนวนจริง (real number line หรือ real line)

การบวกและการคูณของจำนวนจริง มีสมบัติที่สำคัญเช่นเดียวกับสมบัติการบวกและการคูณของจำนวนเต็มที่เราเคยมาแล้ว คือ สมบัติการสลับที่ สมบัติการเปลี่ยนหมู่ สมบัติการแจกแจง สมบัติของหนึ่งและศูนย์

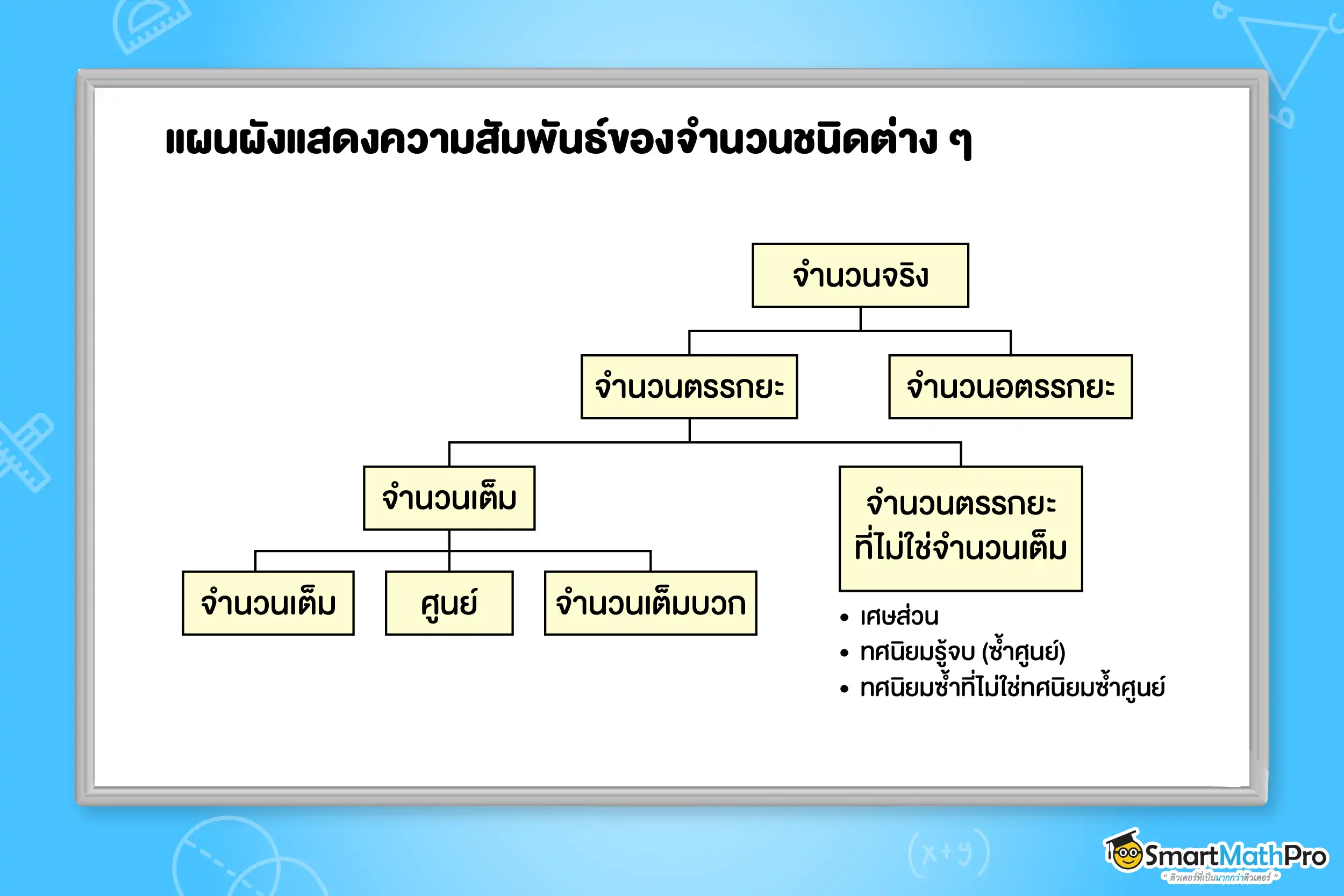
จำนวนที่เป็นจำนวนตรรกยะหรือจำนวนอตรรกยะ เรียกรวมกันว่า จำนวนจริง (Real Number)

จำนวนตรรกยะ

จากที่เราได้รู้แล้วว่าจำนวนจริงคือจำนวนตรรกยะหรือจำนวนอตรรกยะ พี่จะพาน้องมารู้จักจำนวนตรรกยะก่อนเลย
ซึ่งจำนวนตรรกยะมีนิยามดังนี้

บทนิยาม

จำนวนตรรกยะ คือ จำนวนที่เขียนแทนได้ด้วยเศษส่วน $\frac{a}{b}$
เมื่อ $a$ และ $b$ เป็นจำนวนเต็มที่ $b\neq 0$

ตัวอย่างของจำนวนตรรกยะ

จำนวนตรรกยะที่เป็นจำนวนเต็ม ได้แก่
- จำนวนเต็มบวก เช่น $1, 25, 148, 1059, 20578$
- จำนวนเต็มลบ เช่น $-1, -30, -157, -5490, -100000$
- ศูนย์ $(0)$
จำนวนตรรกยะที่อยู่ในรูปของเศษส่วน เช่น \frac{1}{2},\frac{2}{3}, \frac{1}{6}, \frac{3}{4}, \frac{2}{9}, \frac{5}{11}, \frac{7}{12}, \frac{9}{20}, \frac{7}{40}, \frac{11}{25}
เรายังสามารถเขียนเศษส่วนให้อยู่ในรูปของทศนิยมซ้ำได้อีกด้วย ได้แก่
- $\frac{11}{25}=0.44000\ldots=0.44$ (ทศนิยมซ้ำศูนย์)
- $\frac{5}{11}=0.454545…=0.\dot{4}\dot{5}$ (ทศนิยมไม่ซ้ำศูนย์)

จำนวนอตรรกยะ

ในระบบจำนวนจริงอาจมีบางจำนวนที่ไม่สามารถเขียนให้อยู่ในรูปของเศษส่วนหรือทศนิยมซ้ำได้
เราจึงเรียกจำนวนเหล่านี้ว่าจำนวนอตรรกยะนั่นเอง

บทนิยาม

จำนวนอตรรกยะ คือ จำนวนที่ไม่สามารถเขียนแทนได้ด้วยทศนิยมซ้ำหรือเศษส่วน $\frac{a}{b}$
เมื่อ $a$ และ $b$ เป็นจำนวนเต็มที่ $b\neq 0$ ได้

ตัวอย่างของจำนวนอตรรกยะ

จำนวนที่อยู่ในรูปกรณฑ์ เช่น $\sqrt2, 3\sqrt2,\sqrt[3]{2}$
ทศนิยมไม่รู้จบแบบไม่ซ้ำ เช่น $0.19478\ldots, 51.1245\ldots, 697.215486\ldots$
ค่าคงที่ทางคณิตศาสตร์บางค่า เช่น $\pi$

ตัวอย่างที่ 1 จงพิจารณาว่าจำนวนที่กำหนดให้ต่อไปนี้เป็นจำนวนตรรกยะหรือจำนวนอตรรกยะ

$\sqrt5$
ตอบ เป็นจำนวนอตรรกยะ เพราะ $\sqrt5=2.236067\ldots$
เป็นทศนิยมไม่รู้จบแบบไม่ซ้ำจึงไม่สามารถเขียนให้อยู่ในรูปเศษส่วนได้
$\frac{22}{7}$
ตอบ เป็นจำนวนตรรกยะ เพราะ $\frac{22}{7}$ เป็นจำนวนที่อยู่ในรูปของเศษส่วน
$5.231231213312\ldots$
ตอบ เป็นจำนวนอตรรกยะ เพราะ $5.231231213312\ldots$
เป็นทศนิยมไม่รู้จบแบบไม่ซ้ำจึงไม่สามารถเขียนให้อยู่ในรูปเศษส่วนได้
$-1.2343434\ldots$
ตอบ เป็นจำนวนตรรกยะ เพราะ $-1.2343434\ldots$
เป็นทศนิยมซ้ำซึ่งสามารถเขียนให้อยู่ในรูปเศษส่วนได้
$2\frac{3}{5}$
ตอบ เป็นจำนวนตรรกยะ เพราะ $2\frac{3}{5}=\frac{13}{5}$ เป็นจำนวนที่อยู่ในรูปของเศษส่วน

ตัวอย่างที่ 2 จงพิจารณาข้อความต่อไปนี้ว่าเป็นจริงหรือเป็นเท็จ

จำนวนที่ไม่ได้เขียนในรูปเศษส่วนที่เป็นจำนวนเต็มส่วนด้วยจำนวนเต็ม ไม่ใช่จำนวนตรรกยะ
ตอบ เป็นจริง เพราะจำนวนที่ไม่สามารถเขียนในรูปเศษส่วนที่เป็นจำนวนเต็มส่วนด้วยจำนวนเต็ม
คือจำนวนอตรรกยะนั่นเอง
จำนวนอตรรกยะสามารถแทนได้ด้วยจุดบนเส้นจำนวน
ตอบ เป็นจริง เพราะจำนวนอตรรกยะเป็นส่วนหนึ่งของจำนวนจริงซึ่งสามารถเขียนแทนด้วยจุดบนเส้นจำนวนได้
สามารถบอกได้ว่าระหว่าง $1$ และ $3$ มีจำนวนตรรกยะกี่จำนวน
ตอบ เป็นเท็จ เพราะจำนวนตรรกยะไม่ได้มีจำนวนเต็มเพียงอย่างเดียว ยังมีจำนวนที่อยู่ในรูปเศษส่วนหรือทศนิยมซ้ำอีกซึ่งไม่สามารถนับจำนวนได้
ถ้า $a$ และ $b$ เป็นจำนวนเต็มที่ไม่เท่ากับศูนย์ แล้วทั้ง $\frac{a}{b}$ และ $\frac{b}{a}$ ต่างก็เป็นจำนวนตรรกยะ
ตอบ เป็นจริง เพราะทั้ง $\frac{a}{b}$ และ $\frac{b}{a}$ ต่างก็เป็นเศษส่วนที่ตัวส่วนไม่เท่ากับศูนย์นั่นเอง

รากที่สอง

ความหมายของรากที่สอง

รากที่สองของจำนวนจริงใด ๆ จะมีบทนิยามดังนี้

บทนิยาม

ให้ $a$ แทนจำนวนจริงใด ๆ ที่ไม่เป็นลบ
รากที่สอง (square root) ของ $a$
คือ จำนวนจริงที่ยกกำลังสองแล้วได้ $a$

หมายเหตุ : สำหรับรากที่สองของจำนวนจริงลบจะยังไม่กล่าวถึง เนื่องจากไม่มีจำนวนจริงใดที่ยกกำลังสองแล้วได้จำนวนจริงลบ

เราสามารถหารากที่สองของจำนวนจริงบวกใด ๆ โดยใช้บทนิยามได้ดังนี้

$2$ เป็นรากที่สองของ $4$ เพราะว่า $2^2=4$
$-2$ เป็นรากที่สองของ $4$ เพราะว่า ${(-2)}^2=4$
$4$ เป็นรากที่สองของ $16$ เพราะว่า $4^2=16$
$-4$ เป็นรากที่สองของ $16$ เพราะว่า ${(-4)}^2=16$

หรือเราอาจกล่าวได้ว่ารากที่สองของ $4$ ได้แก่ $2, -2$ และรากที่สองของ $16$ ได้แก่ $4, -4$

น้อง ๆ จะเห็นว่าถ้า $a$ เป็นจำนวนจริงบวก รากที่สองของ $a$ มีสองรากคือ รากที่เป็นบวกซึ่งเขียนแทนด้วยสัญลักษณ์ $\sqrt a$ และรากที่เป็นลบซึ่งเขียนแทนด้วยสัญลักษณ์ $-\sqrt a$

มุมความรู้

กรณฑ์ที่สองคือรากที่สองที่เป็นบวก ดังนั้นกรณฑ์ที่สองจะมีเพียงหนึ่งคำตอบเท่านั้น และใช้สัญลักษณ์ $\sqrt{}$
ตัวอย่างเช่น กรณฑ์ที่สองของ $25$ หรือ $\sqrt{25}$ มีค่าเท่ากับ $5$
ส่วนรากที่สองของ $25$ ได้แก่ $\sqrt{25}=5$ และ $-\sqrt{25}=-5$

การหารากที่สอง

การหารากที่สองของจำนวนจริงสามารถทำได้หลายวิธี โดยชั้น ม.2 เราจะเน้นการหารากที่สองโดยการแยกตัวประกอบเท่านั้น ส่วนวิธีอื่น ๆ จะได้เรียนในระดับชั้นที่สูงกว่านี้

ตัวอย่างที่ 3 จงหารากที่สองของจำนวนต่อไปนี้

$1225$
วิธีทำ จาก $1225=5\times5\times7\times7$
$=\left(5\times7\right)^2$
$={35}^2$
ดังนั้น รากที่สองของ $1225$ คือ $35$ และ $-35$
$900$
วิธีทำ จาก $900=2\times2\times3\times3\times5\times5$
$=\left(2\times3\times5\right)^2$
$={30}^2$
ดังนั้น รากที่สองของ $900$ คือ $30$ และ $-30$

การเปรียบเทียบจำนวนที่อยู่ในรูปกรณฑ์ที่สอง

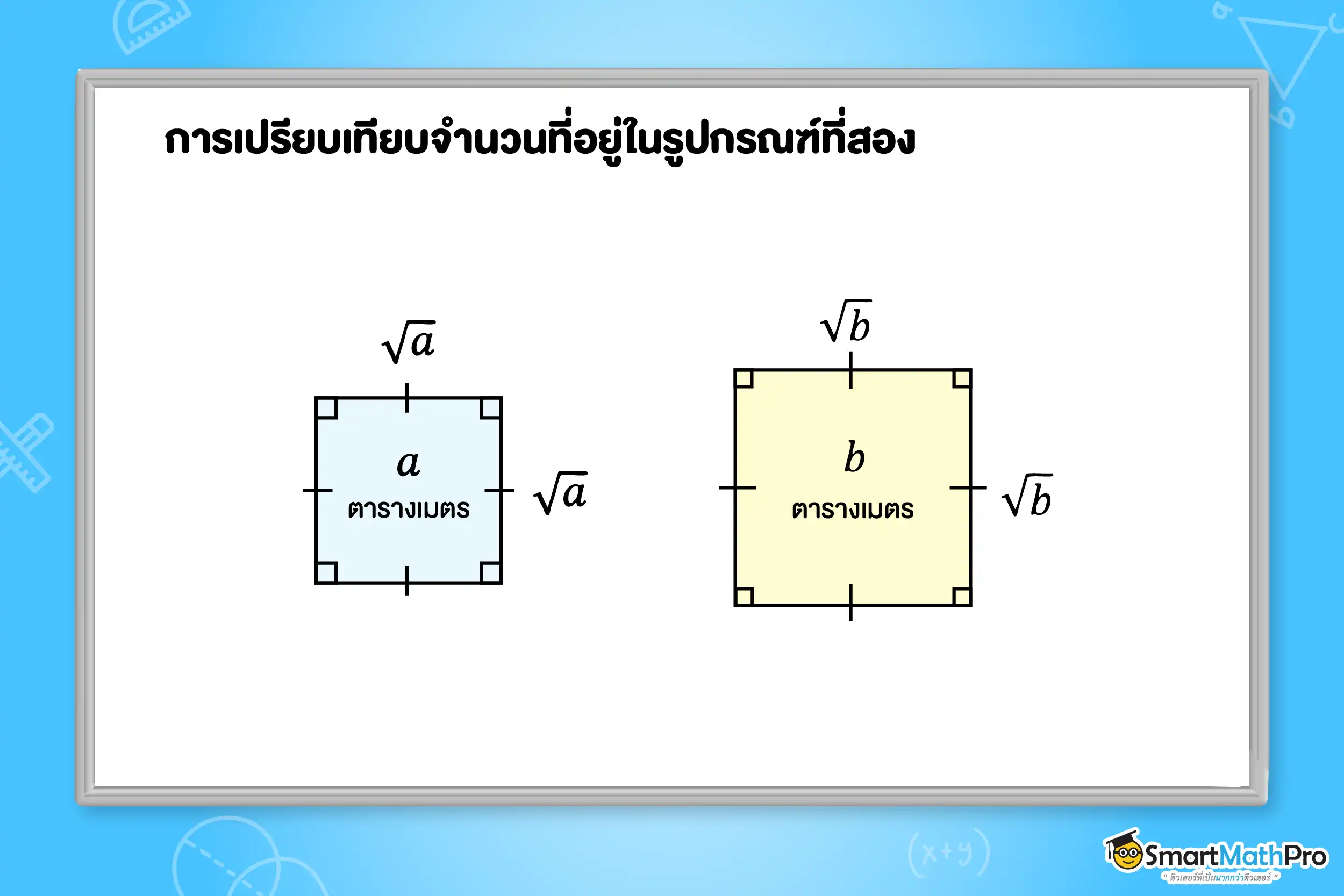
จากรูปน้อง ๆ จะเห็นว่าพื้นที่ของรูปสี่เหลี่ยมจัตุรัสที่เล็กกว่าอีกรูปหนึ่ง จะมีความยาวด้านของรูปที่มีพื้นที่เล็กกว่าก็จะสั้นกว่าอีกรูปหนึ่งไปด้วย ดังนั้น ถ้าเราเทียบพื้นที่ของรูปสี่เหลี่ยมจัตุรัสซึ่งได้ว่า $a<b$ ก็จะสรุปความสัมพันธ์ของความยาวด้านทั้งสองรูปได้ว่า $\sqrt a<\sqrt b$ ด้วย

สมบัติ

กำหนดให้ $a>0, b>0$

ถ้า $a<b$ แล้ว $\sqrt{a}<\sqrt{b}$
$\sqrt{a}\cdot \sqrt{b}=\sqrt{ab}$
$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$

ตัวอย่างที่ 4 $\sqrt{10}$ และ $\sqrt{9.5}$ จำนวนใดมีค่ามากกว่ากัน

วิธีทำ จากสมบัติ ถ้า $a>0, b>0$ และ $a<b$ แล้ว $\sqrt a<\sqrt b$
และ $10>9.5$
ดังนั้น $\sqrt{10}$ มีค่ามากกว่า $\sqrt{9.5}$

รากที่สาม

ความหมายของรากที่สาม

รากที่สามของจำนวนจริงใด ๆ จะมีบทนิยามดังนี้

บทนิยาม

ให้ $a$ แทนจำนวนจริงใด ๆ รากที่สาม (cube root) ของ $a$
คือ จำนวนจริงที่ยกกำลังสามแล้วได้ $a$
เขียนแทนด้วยสัญลักษณ์ $\sqrt[3]{a}$

หมายเหตุ : $\sqrt[3]{a}$ อ่านว่า กรณฑ์ที่สามของ $a$
เราสามารถหารากที่สามของจำนวนจริงบวกใด ๆ โดยใช้บทนิยามได้ดังนี้

$2$ เป็นรากที่สามของ $8$ เพราะว่า $2^3=8$
$-2$ เป็นรากที่สามของ $-8$ เพราะว่า ${(-2)}^3=-8$
$3$ เป็นรากที่สามของ $27$ เพราะว่า $3^3=27$
$-3$ เป็นรากที่สามของ $-27$ เพราะว่า ${(-3)}^3=-27$

น้อง ๆ จะเห็นว่าเราสามารถหาค่าของรากที่สามหรือกรณฑ์ที่สามของ $a$ ที่เป็นจำนวนจริงลบได้ และรากที่สามของจำนวนจริง $a$ จะมีค่าเดียว และมีค่าเท่ากับกรณฑ์ที่สามของ $a$

การหารากที่สาม

เราสามารถหารากที่สามโดยใช้วิธีการแยกตัวประกอบได้ โดยใช้แนวคิดคล้ายกันกับการหารากที่สองเลยย

ตัวอย่างที่ 5 จงหารากที่สามของจำนวนต่อไปนี้

$216$
วิธีทำ จาก $216=2\times2\times2\times3\times3\times3$
$=\left(2\times3\right)^3$
$=6^2$
ดังนั้น รากที่สามของ $216$ คือ $6$
$-343$
วิธีทำ จาก $-343=\left(-7\right)\times\left(-7\right)\times\left(-7\right)$
$=\left(-7\right)^3$
ดังนั้น รากที่สามของ $-343$ คือ $-7$

การเปรียบเทียบจำนวนที่อยู่ในรูปกรณฑ์ที่สาม

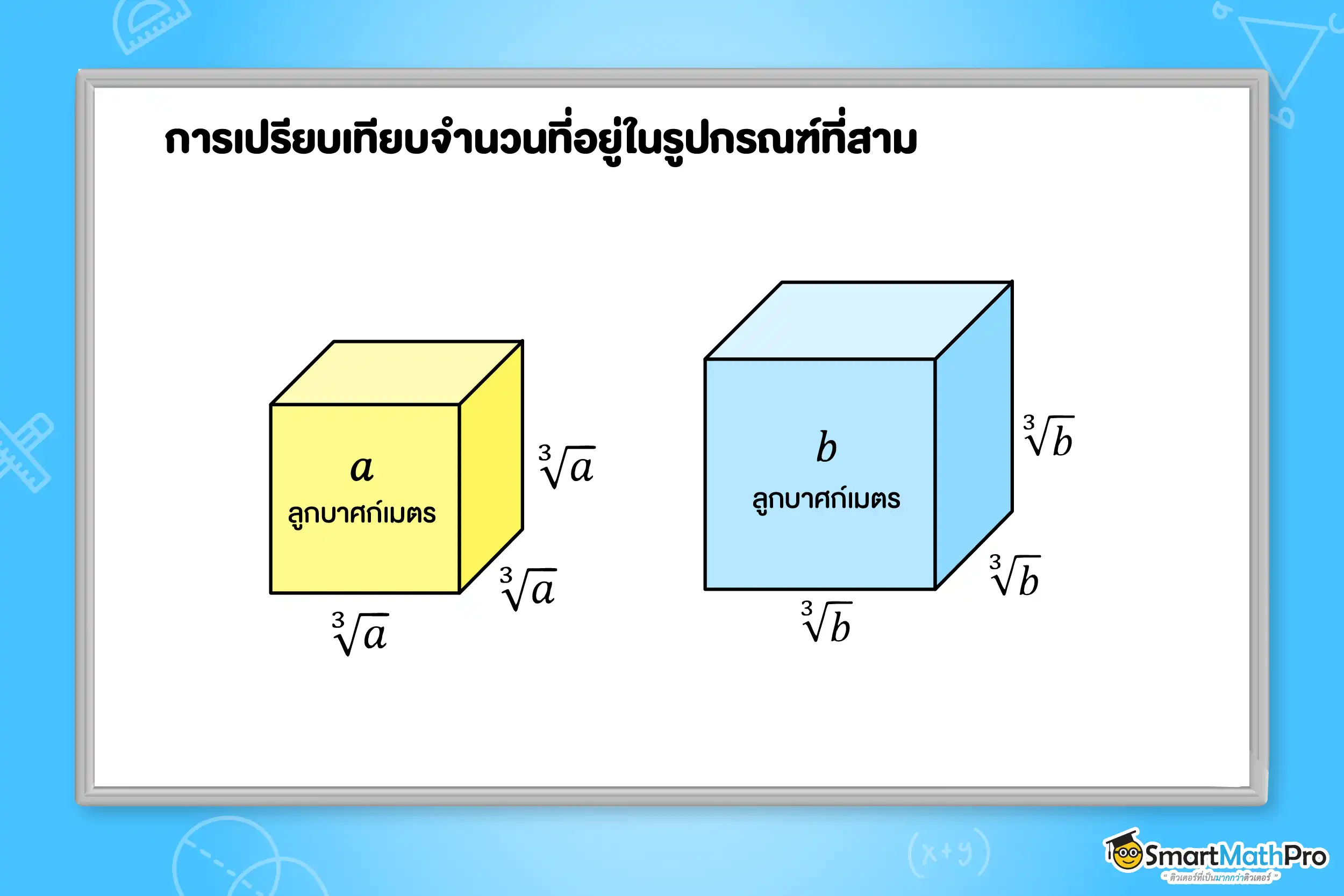
จากรูป ถ้าปริมาตรของลูกบาศก์น้อยกว่าอีกลูกบาศก์หนึ่ง แล้วความยาวด้านของลูกบาศก์ที่มีปริมาตรน้อยกว่าก็จะสั้นกว่าอีกลูกบาศก์หนึ่งไปด้วย ดังนั้น ถ้าเทียบปริมาตรของลูกบาศก์ซึ่งได้ว่า $a<b$ ก็จะจึงสรุปความสัมพันธ์ของความยาวด้านของลูกบาศก์ทั้งสองได้ว่า $\sqrt[3]{a}<\sqrt[3]{b}$ นั่นเอง

สมบัติ

กำหนดให้ $a,b$ และ $c$ เป็นจำนวนจริง

ถ้า $a<b$ แล้ว $\sqrt[3]{a}<\sqrt[3]{b}$
$\sqrt[3]{a}\cdot \sqrt[3]{b}=\sqrt[3]{ab}$
$\frac{\sqrt[3]{a}}{\sqrt[3]{b}}=\sqrt[3]{\frac{a}{b}}$
$\left ( \sqrt[3]{a} \right )^{3}=a$
$a\times (b+c)=(a\times b)+(a\times c)$

ตัวอย่างที่ 6 $\sqrt[3]{42}$ และ $\sqrt[3]{45}$ จำนวนใดมีค่าน้อยกว่ากัน
วิธีทำ จากสมบัติ ถ้า $a>0, b>0$ และ $a<b$ แล้ว $\sqrt[3]{a}<\sqrt[3]{b}$
และ $42<45$
ดังนั้น $\sqrt[3]{42}$ มีค่าน้อยกว่า $\sqrt[3]{45}$

ติวคณิตศาสตร์ ม.ต้น กับ SmartMathPro

สำหรับน้อง ๆ ม.2 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์

พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.2 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน แนวข้อสอบเข้าม.4 และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก เลย

อ่านกันมาจนถึงตรงนี้ พี่คิดว่าน้อง ๆ น่าจะเข้าใจเรื่องจำนวนจริง ม.2 กันมากขึ้นแล้ว โดยพี่แนะนำให้ทำแบบฝึกหัดเรื่องนี้บ่อย ๆ เพราะจะช่วยให้แม่นยำในเนื้อหามากขึ้น ซึ่งนอกจากตัวอย่างโจทย์ให้ดูในบทความนี้แล้ว พี่ยังมีแบบฝึกหัดให้ลองทำเพิ่มเติมด้วยน้าา