เนื้อหาเรื่องพื้นที่และปริมาตร เป็นเนื้อหาที่จะพบทั้งในคณิต ม.2 และคณิต ม.3 แต่บทความนี้จะเน้นที่เนื้อหา ปริซึมและทรงกระบอก ม.2 ก่อนน้า
โดยในบทความนี้ พี่จะพาน้อง ๆ ไปรู้จักปริซึมและทรงกระบอกให้มากยิ่งขึ้น ทั้งเรื่องความหมาย, ส่วนประกอบ, พื้นที่ผิว, ปริมาตร พร้อมแจกแบบฝึกหัด+เฉลยให้น้อง ๆ ได้ลองทำกันท้ายบทความด้วยน้าา
ปริซึม คืออะไร ?
ก่อนหน้านี้ในระดับชั้นประถมศึกษา น้อง ๆ ได้เรียนรูปเรขาคณิตสามมิติกันมาบ้างแล้วใช่ไหม แต่ในระดับชั้น ม.2 นี้ เราจะมาทำความรู้จักกับรูปเรขาคณิตสามมิติที่เรียกว่า ปริซึม (prism) โดยจะมีลักษณะ คือ มีฐานทั้งสองเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการ ฐานทั้งสองอยู่บนระนาบที่ขนานกัน และด้านข้างแต่ละด้านเป็นรูปสี่เหลี่ยมด้านขนาน
หลายคนอาจจะไม่คุ้นเคยคำว่า “ปริซึม” แต่จริง ๆ แล้ว เป็นสิ่งที่พบเจอได้ในชีวิตประจำวันเลยน้า เช่น กล่องลังมีลักษณะเป็นปริซึมฐานสี่เหลี่ยมมุมฉาก หมอนอิงสามเหลี่ยมมีลักษณะเป็นปริซึมฐานสามเหลี่ยม
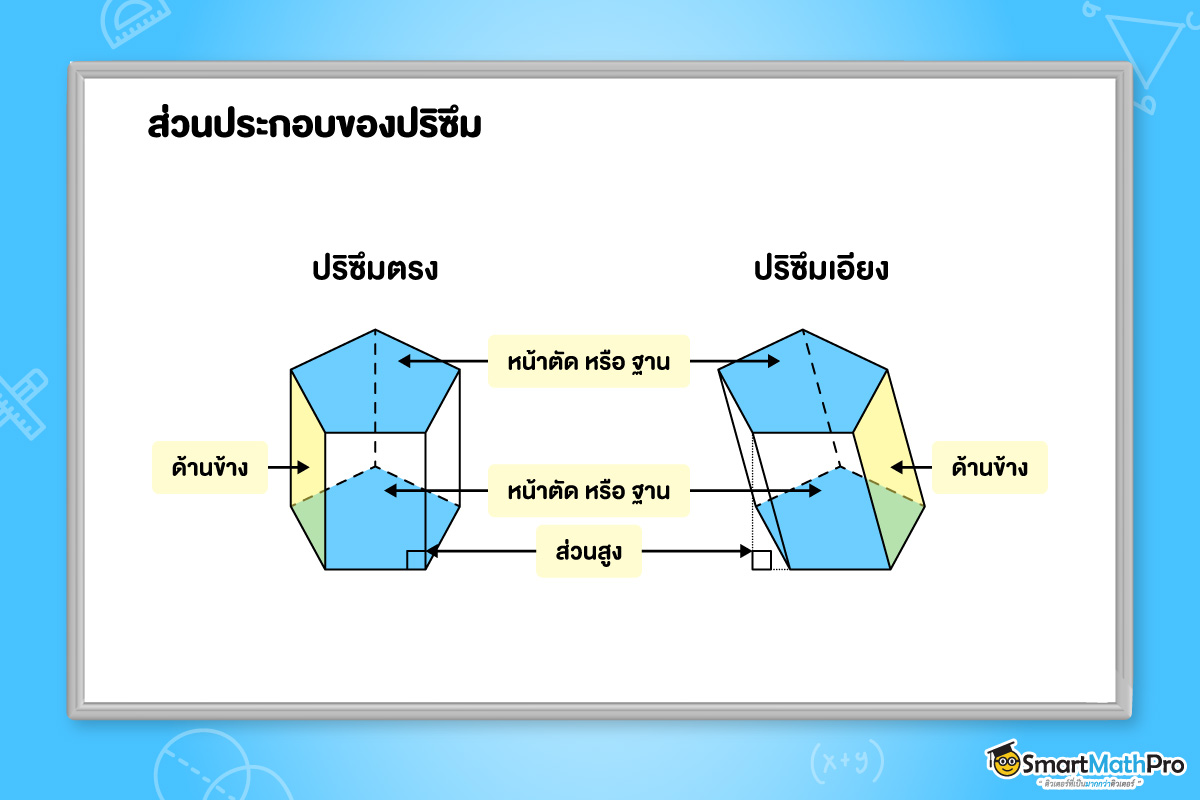
ส่วนประกอบของปริซึม
ปริซึมมี 2 แบบ คือ ปริซึมตรงและปริซึมเอียง โดยปริซึมตรงจะมีด้านข้างเป็นรูปสี่เหลี่ยมมุมฉาก แต่ปริซึมเอียงจะมีด้านข้างเป็นรูปสี่เหลี่ยมด้านขนานที่แต่ละมุมไม่เป็นมุมฉาก
ซึ่งในระดับชั้น ม.2 นี้จะกล่าวถึงปริซึมตรงเท่านั้นน้า โดยเราจะเรียกส่วนประกอบของปริซึมในแต่ละส่วน ดังรูปนี้
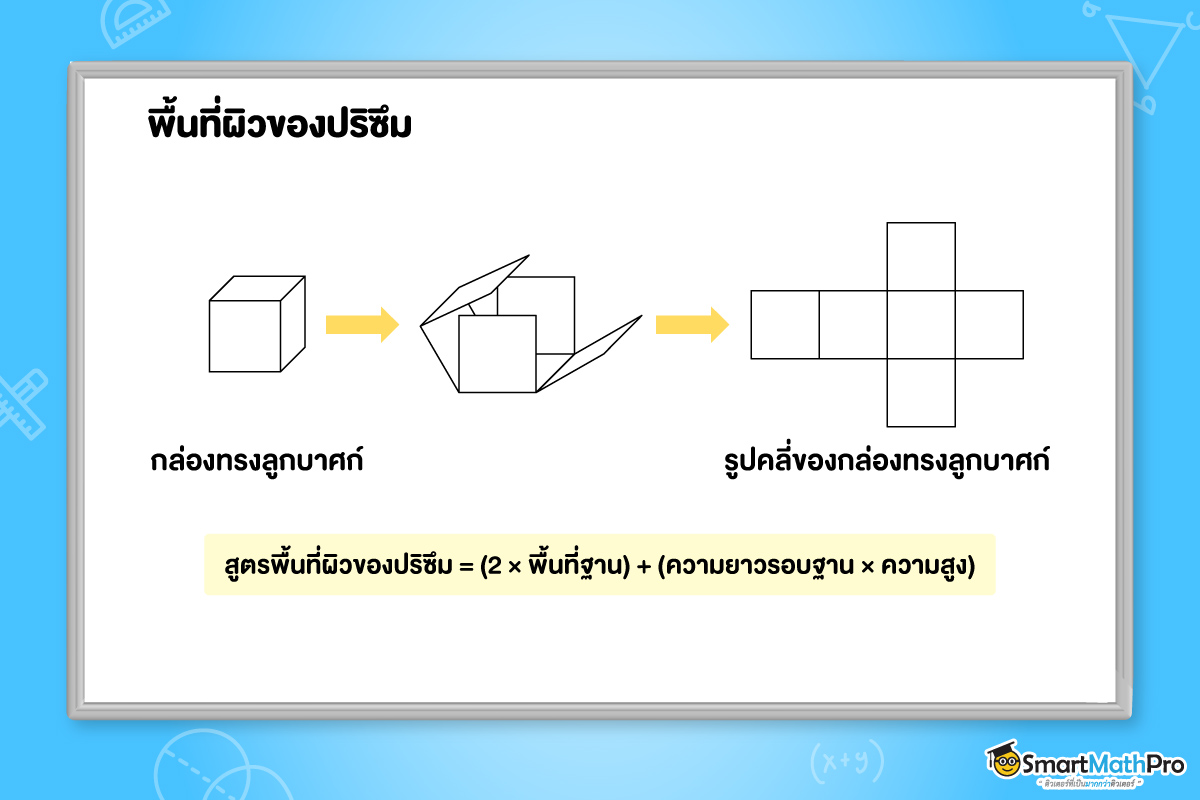
พื้นที่ผิวของปริซึม
การหาพื้นที่ผิวของปริซึม คือ การหาพื้นที่ของด้านข้างทั้งหมดหรือพื้นที่ผิวข้าง รวมกับ พื้นที่ของฐานทั้งสอง
น้อง ๆ สามารถร่างภาพรูปคลี่ คือรูปเรขาคณิตสองมิติที่แสดงหน้าแต่ละหน้าของรูปเรขาคณิตสามมิติที่คลี่ออกมาจากบริเวณที่เป็นสันหรือเส้นขอบก่อน แล้วนำไปคำนวณเพื่อหาพื้นที่ผิวต่อไป โดยการหาพื้นที่ผิวของปริซึมสามารถหาได้จากสูตรต่อไปนี้
เพื่อให้เข้าใจมากขึ้น เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กันเลย
ตัวอย่างที่ 1 จงหาพื้นที่ผิวของปริซึมนี้
ตัวอย่างที่ 2 ห้องประชุมหนึ่งเป็นห้องทรงสี่เหลี่ยมมุมฉากกว้าง 6 เมตร ยาว 10 เมตร และสูง 3 เมตร ช่างต้องการทาสีเพดานและผนังภายในห้องทั้ง 4 ด้าน (ไม่ทาสีบริเวณพื้น) ช่างต้องทาสีคิดเป็นพื้นที่ทั้งหมดกี่ตารางเมตร
วิธีทำ พื้นที่เพดานของห้องประชุม คือ 6\times 10=60 ตารางเมตร
ความยาวรอบห้องประชุม คือ 6+10+6+10=32 เมตร
ความสูงของห้องประชุม คือ 3 เมตร
ดังนั้น ช่างต้องทาสีพื้นที่ทั้งหมด 60+(32\times 3)=156 ตารางเมตร
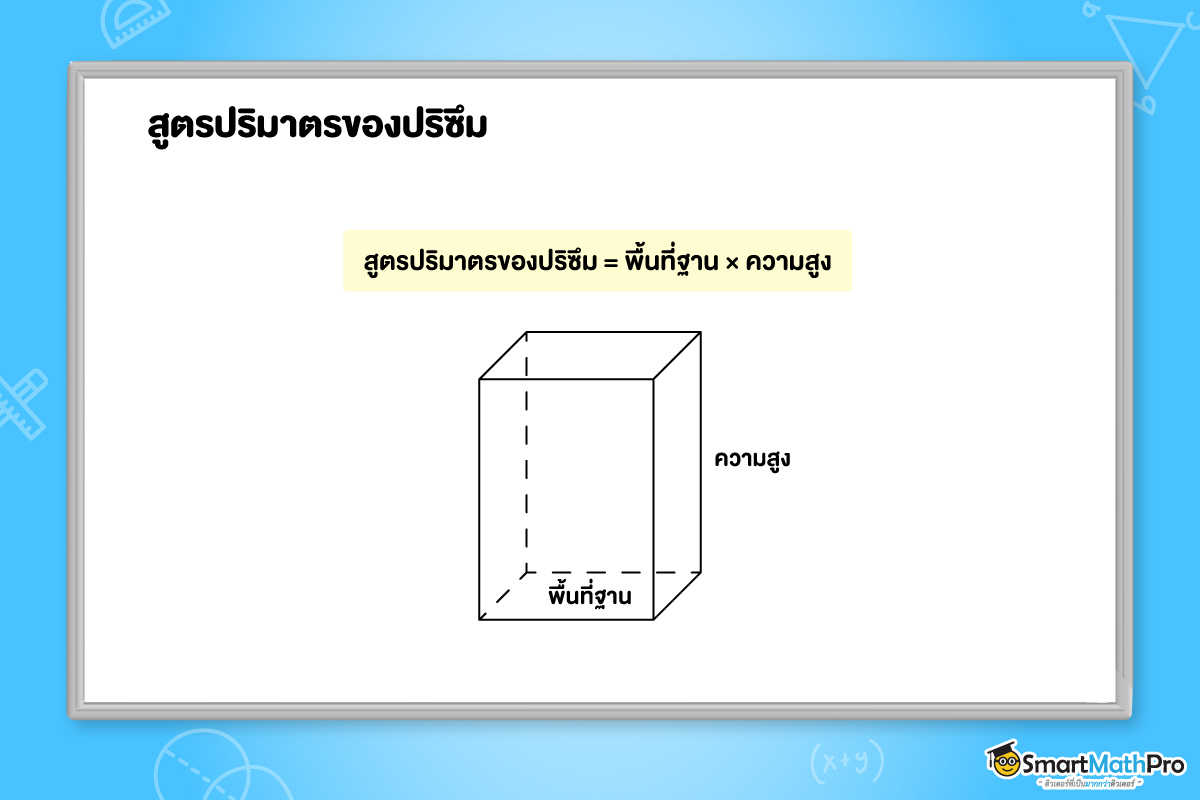
ปริมาตรของปริซึม
โดยทั่วไป เรามักจะกล่าวถึงปริมาตรของของแข็งที่มีรูปทรงเรขาคณิต และสามารถใช้ความรู้เรื่องปริมาตรของปริซึมในชีวิตประจำวันได้โดยการนำไปใช้เปรียบเทียบราคาของสินค้าต่อหน่วยปริมาตร
ซึ่งจะช่วยให้เราตัดสินใจซื้อสินค้าที่ถูกและคุ้มค่ากว่าได้ โดยการคำนวณหาปริมาตรของปริซึม
สามารถทำได้โดยใช้สูตรต่อไปนี้
เพื่อให้น้อง ๆ เข้าใจมากขึ้นและสามารถนำไปใช้ได้ เราลองไปใช้สูตรผ่านตัวอย่างต่อไปนี้กันเลย
ตัวอย่างที่ 3 จงหาปริมาตรของปริซึมนี้
ตัวอย่างที่ 4 ถังทรงสี่เหลี่ยมมุมฉากยาว 15 เมตร กว้าง 10 เมตร ถ้าต้องการเก็บน้ำไว้ในถัง 975 ลูกบาศก์เมตร แล้วน้ำจะสูงจากก้นถังเท่าใด
วิธีทำ ปริมาตรถังทรงสี่เหลี่ยมมุมฉาก = พื้นที่ฐาน \times ความสูง
ต้องการเก็บน้ำไว้ในถัง 975 ลูกบาศก์เมตร
จะได้ 975=15\times10\times ความสูง
ดังนั้น ความสูงของน้ำจากก้นถัง คือ \frac{975}{150} = 6.5 975150 = 150 เมตร
ทรงกระบอก คืออะไร ?
หลังจากที่เราทำความรู้จักกับปริซึมแล้ว ในหัวข้อนี้เราจะมาทำความรู้จักกับรูปเรขาคณิตสามมิติที่เรียกว่าทรงกระบอก โดยทรงกระบอกเป็นรูปเรขาคณิตสามมิติที่มีรูปร่างคล้ายกระบอกไม้ไผ่ที่ตัดเป็นท่อนนั่นเอง
และในทางคณิตศาสตร์ ทรงกระบอก (cylinder) คือ รูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นวงกลมที่เท่ากันทุกประการ และอยู่บนระนาบที่ขนานกัน เมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกันกับฐาน จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกับฐานเสมอ
น้อง ๆ อาจจะคุ้นเคยกับทรงกระบอกเพราะวัตถุหรือสิ่งของหลายสิ่งในชีวิตประจำวันของเรามีคำว่ากระบอกอยู่ในชื่อ เพื่อให้รู้ว่ามีส่วนที่เกี่ยวข้องกับทรงกระบอก เช่น เสื้อแขนกระบอก หุ่นกระบอก และสิ่งของอีกหลายสิ่งที่ส่วนประกอบมีลักษณะเป็นทรงกระบอก เช่น แก้วน้ำ กระป๋อง แจกัน ถ่านไฟฉาย
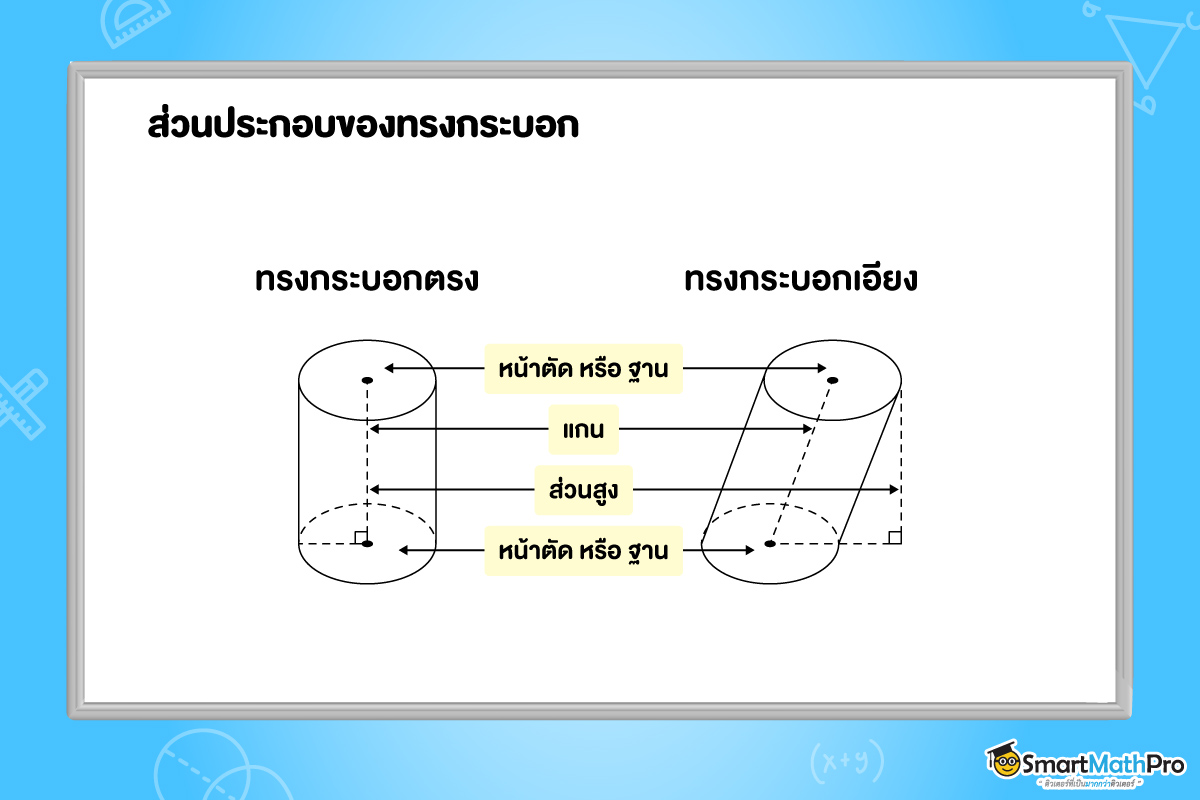
ส่วนประกอบของทรงกระบอก
ทรงกระบอกจะมีทรงกระบอกตรงและทรงกระบอกเอียง ซึ่งในระดับชั้นม.2 นี้จะกล่าวถึงทรงกระบอกตรงเท่านั้น ซึ่งทรงกระบอกตรงเป็นทรงกระบอกที่มีแกนตั้งฉากกับฐาน โดยเราจะเรียกส่วนประกอบของปริซึมในแต่ละส่วน ดังรูปนี้
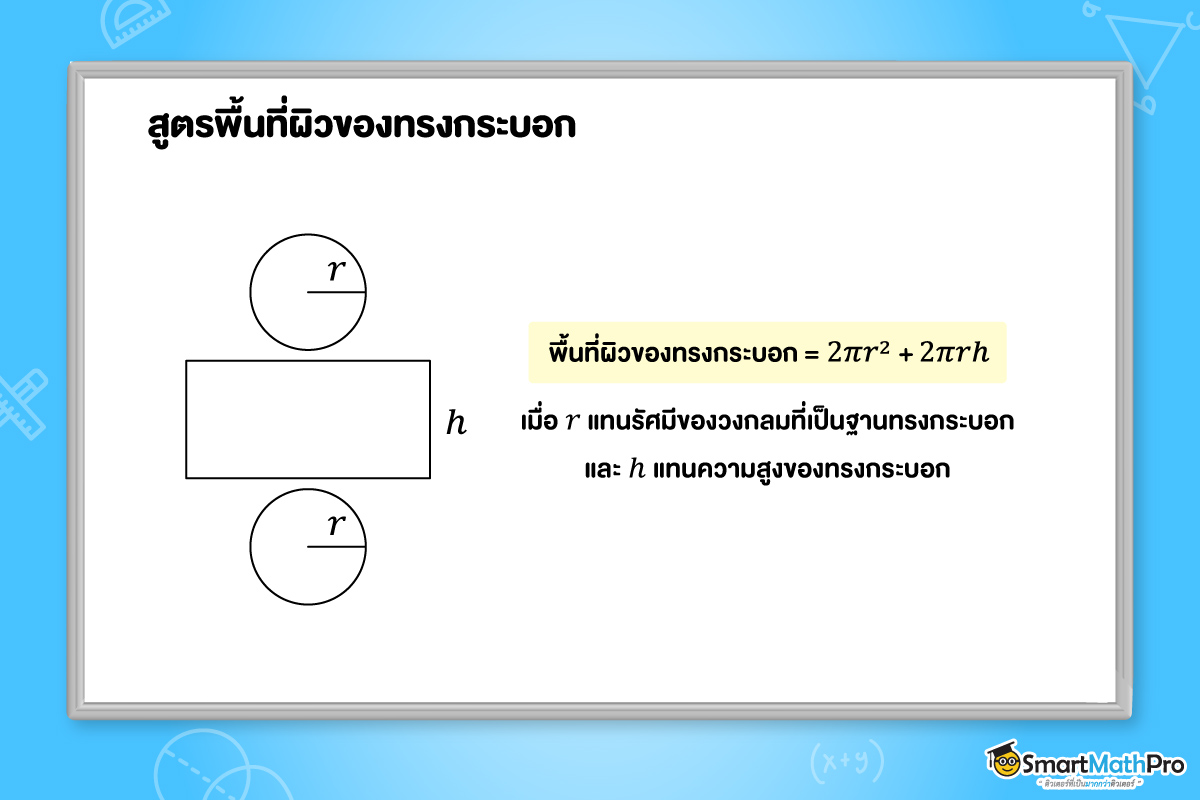
พื้นที่ผิวของทรงกระบอก
การหาพื้นที่ผิวของทรงกระบอกใช้แนวคิดเหมือนกันกับหาพื้นที่ผิวของปริซึม โดยจะนำพื้นที่หน้าตัดทั้งสองรวมกับพื้นที่ผิวข้าง โดยการหาพื้นที่ผิวของทรงกระบอกสามารถหาได้จากสูตรต่อไปนี้
เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราลองดูตัวอย่างต่อไปนี้กันเลย
ตัวอย่างที่ 5 จงหาพื้นที่ผิวของทรงกระบอกต่อไปนี้ (กำหนดให้ \pi \approx \frac{22}{7} )
ตัวอย่างที่ 6 พี่พลอยต้องการห่อของขวัญกล่องคุกกี้ที่มีลักษณะเป็นทรงกระบอก โดยมีเส้นผ่านศูนย์กลางยาว 20 เซนติเมตร และสูง 8 เซนติเมตร พี่พลอยจะต้องใช้กระดาษห่อของขวัญอย่างน้อยกี่ตารางเซนติเมตร (กำหนดให้ \pi \approx 3.14 )
วิธีทำ จากโจทย์ เส้นผ่านศูนย์กลางของกล่องคุกกี้ยาว 20 เซนติเมตร นั่นคือ รัศมีของกล่องคุกกี้ยาว \frac{20}{2}=10 เซนติเมตร และกล่องคุกกี้สูง 8 เซนติเมตร
นั่นคือ กล่องคุกกี้นี้มี r=10 และ h=8
จากสูตรหาพื้นที่ผิวของทรงกระบอก =2\pi r^2+2\pi rh
เมื่อแทนค่าลงในสูตร จะได้ว่า พื้นที่ผิวของกล่องคุกกี้ ประมาณ (2\times 3.14\times10^2)+(2\times3.14\times10\times8)\approx 1,130.4 ตารางเซนติเมตร
ดังนั้น พี่พลอยจะต้องใช้กระดาษห่อของขวัญอย่างน้อย 1,130.4 ตารางเซนติเมตร
ปริมาตรของทรงกระบอก
การหาปริมาตรของทรงกระบอกใช้แนวคิดเหมือนกันกับการหาปริมาตรของปริซึม โดยพื้นที่หน้าตัดคูณกับความสูงของทรงกระบอก สามารถหาปริมาตรของทรงกระบอกได้จากสูตรต่อไปนี้
ลองฝึกใช้สูตรผ่านตัวอย่างต่อไปนี้กัน
ตัวอย่างที่ 7 จงหาปริมาตรของทรงกระบอกนี้ (กำหนดให้ \pi \approx \frac{22}{7} )
ตัวอย่างที่ 8 กระบอกน้ำดื่มใบหนึ่งสูง 22 เซนติเมตร เส้นรอบวงของปากกระบอกยาว 25.12 เซนติเมตร จงหาว่าความจุของกระบอกน้ำใบนี้เท่ากับเท่าใด (กำหนดให้ \pi \approx 3.14 )
วิธีทำ จากโจทย์ เส้นรอบวงของปากกระบอกยาว 25.12 เซนติเมตร
จากสูตรความยาวเส้นรอบวง เท่ากับ 2\pi r
จะได้ว่า 25.12=2\times 3.14\times r
r=\frac{25.12}{2\times 3.14}=4 เซนติเมตร
นั่นคือกระบอกน้ำนี้มี r=4 และ h=22
จากสูตรหาปริมาตรทรงกระบอก =\pi r^2 h
เมื่อแทนค่าลงในสูตร จะได้ว่า ความจุของกระบอกน้ำใบนี้ ประมาณ 3.14\times 4^2\times22\approx 1,105.28 ลูกบาศก์เซนติเมตร
ติวคณิตศาสตร์ ม.ต้น กับ SmartMathPro
พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.2 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน แนวข้อสอบเข้าม.4 และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก เลย
อ่านกันมาจนถึงตรงนี้ พี่คิดว่าน้อง ๆ น่าจะเข้าใจเรื่องปริซึมและทรงกระบอก (พื้นที่และปริมาตร) ม.2 กันมากขึ้นแล้ว
ซึ่งพี่แนะนำให้ทำแบบฝึกหัดเรื่องนี้บ่อย ๆ เพราะจะช่วยให้แม่นยำในเนื้อหามากขึ้น ซึ่งนอกจากตัวอย่างโจทย์ให้ดูในบทความนี้แล้ว พี่ยังมีแบบฝึกหัดให้ลองทำเพิ่มเติมด้วยน้าา >> แบบฝึกหัดปริซึมและทรงกระบอก (พื้นที่และปริมาตร) ม.2
บทความ แนะนำ
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
พี่เนย ทีมวิชาการคณิตศาสตร์ SmartMathPro
ป.ตรี คณะวิทยาศาสตร์ สาขาวิชาคณิตศาสตร์ มศว
พี่สาวที่ชอบวิชาคณิตศาสตร์กับเลข 12 พร้อมแบ่งปันและ
อธิบายความรู้ทางคณิตศาสตร์ให้น้อง ๆ เข้าใจได้ง่ายขึ้น
พี่เนย ทีมวิชาการคณิตศาสตร์ SmartMathPro
ป.ตรี คณะวิทยาศาสตร์ สาขาวิชาคณิตศาสตร์ มศว
พี่สาวที่ชอบวิชาคณิตศาสตร์กับเลข 12 พร้อมแบ่งปันและอธิบายความรู้ทางคณิตศาสตร์ให้น้อง ๆ เข้าใจได้ง่ายขึ้น
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
