สรุป แสงเชิงคลื่น ฟิสิกส์ ม.5 พร้อมโจทย์และเฉลย

เนื้อหาเรื่อง แสง ฟิสิกส์ เป็น 1 เนื้อหาที่มีรายละเอียดค่อนข้างเยอะ ซึ่งพี่แบ่งเนื้อหาดังกล่าวออกเป็น 2 เรื่องหลัก คือ แสงเชิงคล่ืนและแสงเชิงรังสี แต่ในบทความนี้จะพูดถึงแค่เรื่องแสงเชิงคล่ืนก่อนน้า เพราะอยากให้ทุกคนค่อย ๆ ทำความเข้าใจไปทีละเรื่อง

โดยพี่เตรียมสรุปเรื่องนิยาม แหล่งกำเนิดแสง และเนื้อหาสำคัญอื่น ๆ พร้อมกับพาทบทวนเรื่องสูตรต่าง ๆ และมีตัวอย่างข้อสอบท้ายบทความให้ทุกคนได้ลองฝึกทำอีกด้วยยย !!

สนใจหัวข้อไหน ... กดอ่านเลย

แสงคืออะไร ?

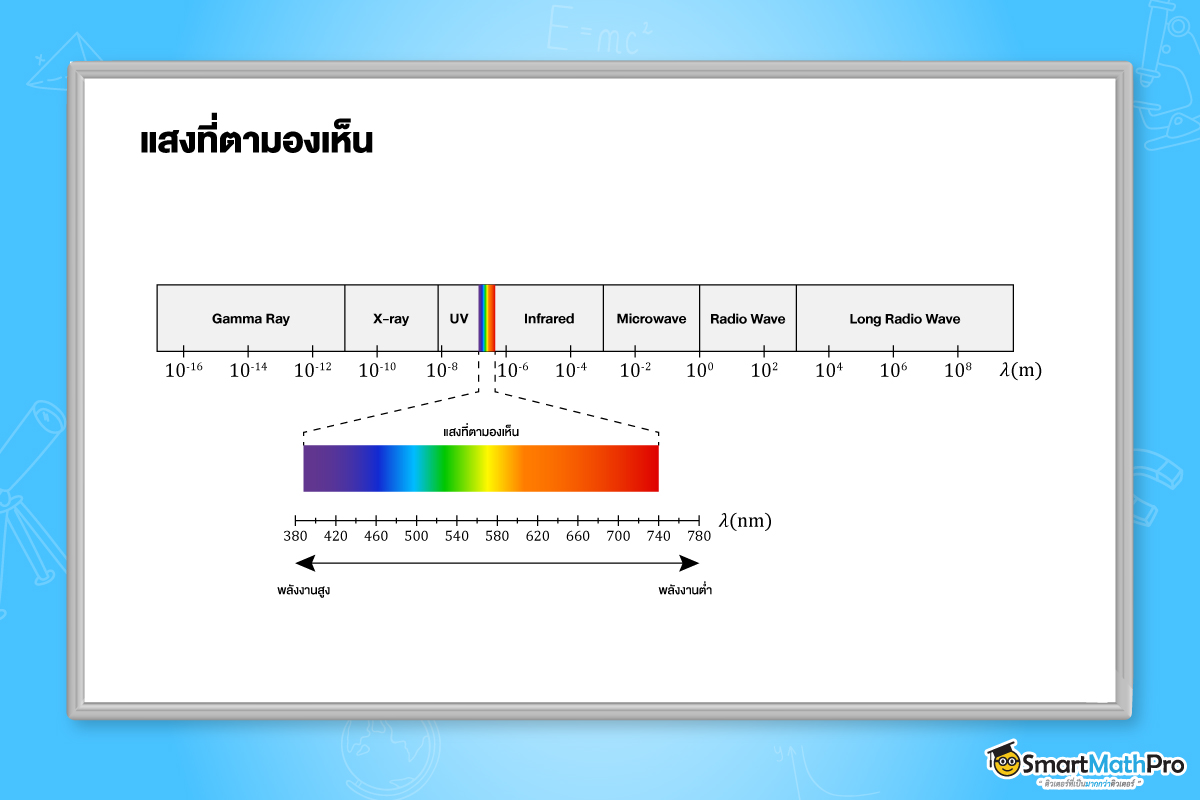
แสง (Light) เป็นคล่ืนแม่เหล็กไฟฟ้า (Electromagnetic Wave) ชนิดหนึ่ง ซึ่งมีความยาวคล่ืนอยู่ในช่วงที่มนุษย์สามารถรับรู้ได้ผ่านดวงตาหรือที่เรียกว่า “แสงที่ตามองเห็น” (Visible Light)

แสงที่ตามองเห็นเป็นส่วนหนึ่งของ สเปกตรัมแม่เหล็กไฟฟ้า โดยมีความยาวคล่ืนอยู่ในช่วง $400-700$ นาโนเมตร และมีอัตราเร็วในสุญญากาศประมาณ $3\times 10^{8}$ เมตรต่อวินาที ซึ่งเท่ากับความเร็วของคล่ืนแม่เหล็กไฟฟ้าทุกชนิด

แหล่งกำเนิดแสง

แหล่งกำเนิดแสง หมายถึง วัตถุหรือสิ่งที่สามารถปล่อยแสงออกมาได้เอง ซึ่งสามารถแบ่งออกเป็น 2 ประเภทหลัก ได้แก่

แหล่งกำเนิดแสงตามธรรมชาติ เช่น
- ดวงอาทิตย์ (Sun) เป็นแหล่งกำเนิดแสงที่สำคัญของโลก
- ดาวฤกษ์ (Stars) อื่น ๆ ที่ปล่อยพลังงานออกมาในรูปของแสง
- ฟ้าแลบ ฟ้าผ่า (Lightning) ซึ่งเกิดจากการปลดปล่อยพลังงานไฟฟ้าในบรรยากาศ
- หิ่งห้อย และ สัตว์เรืองแสง (Bioluminescent organisms) เช่น แมงกะพรุนเรืองแสง
แหล่งกำเนิดแสงที่มนุษย์สร้างขึ้น เช่น
- หลอดไฟฟ้า เช่น หลอดไส้ (Incandescent bulb) และหลอดฟลูออเรสเซนต์
- LED (Light Emitting Diode) ที่ใช้ในจอภาพและไฟส่องสว่าง
- เลเซอร์ (Laser) ที่ใช้ในอุปกรณ์ทางวิทยาศาสตร์และการแพทย์
- เปลวไฟ จากเทียน ไฟแช็ก หรือเตาเผาต่าง ๆ

สมบัติและพฤติกรรมของแสง

การสะท้อน (Reflection)

ปรากฏการณ์ที่แสงเดินทางไปกระทบพื้นผิวของวัตถุแล้วเปลี่ยนทิศทางการเคลื่อนที่กลับสู่ตัวกลางเดิม การสะท้อนของแสงขึ้นอยู่กับคุณสมบัติของพื้นผิวสัมผัส ซึ่งอาจเป็นการสะท้อนแบบปกติหรือการสะท้อนแบบกระจาย ขึ้นอยู่กับลักษณะของพื้นผิวนั้น ๆ

การหักเห (Refraction)

ปรากฏการณ์ที่แสงเดินทางเคลื่อนที่ผ่านตัวกลางที่มีดัชนีหักเหแตกต่างกัน เช่น อากาศ แก้ว หรือ น้ำ ส่งผลให้เกิดการเปลี่ยนแปลงความเร็วของแสงและอาจจะเปลี่ยนแปลงทิศทาง ซึ่งเป็นเหตุผลที่ทำให้วัตถุที่อยู่ในน้ำดูเหมือนบิดเบี้ยว
จากตำแหน่งจริง

การแทรกสอดของแสง (Interference)

ปรากฏการณ์ที่เกิดขึ้นเมื่อคลื่นแสง 2 ขบวนเคลื่อนที่มาพบกัน จะเกิดการรวมตัวกันและแทรกสอดกันเกิดเป็นแถบมืดและแถบสว่างบนฉาก การที่จะเกิดการแทรกสอดที่สังเกตได้ชัดเจน แหล่งกำเนิดแสงที่มาซ้อนทับกันจะต้องเป็นแหล่งกำเนิดอาพันธ์ (Coherent Source) คือเป็นแหล่งกำเนิดที่ให้คลื่นแสงความถี่เดียวกัน และความยาวคลื่นเท่ากันและมีผลต่างเฟสคงที่ ตำแหน่งปฏิบัพจะเป็นแถบสว่าง ส่วนตำแหน่งบัพจะเป็นแถบมืด

การเล้ียวเบนของแสง (diffraction)

ปรากฏการณ์ที่แสงเลี้ยวรอบสิ่งกีดขวาง หรือ เลี้ยวเบนผ่านช่องแคบ ทำให้เกิดการกระจายแสงไปบริเวณด้านหลังของวัตถุทึบแสงได้ การเลี้ยวเบนของแสงเกิดขึ้นได้ชัดเจนเมื่อแสงจากแหล่งกำเนิดแสงอาพันธ์เดินทางผ่านช่องแคบที่มีขนาดเล็ก ใกล้เคียงกับความยาวคลื่นแสง

Tips : Timeline ของการศึกษาแสงเชิงคล่ืน

การศึกษาเรื่องราวของแสงมีการพัฒนาและการเปล่ียนแปลงจากแนวคิดของนักวิทยาศาสตร์ที่สำคัญหลายคนในช่วงเวลาต่างๆ ตั้งแต่อดีตจนถึงปัจจุบัน ดังนี้

– ศตวรรษที่ 17 (ค.ศ.1601 – ค.ศ. 1701)

– ไอแซก นิวตัน (Isaac Newton) ได้ตั้งทฤษฎีอนุภาคโดยกล่าวว่าแสงเป็นอนุภาคที่ถูกส่งออกจากต้นกำเนิดแสง อนุภาคเหล่านี้เคล่ือนที่เป็นเส้นตรงสามารถทะลุผ่านวัตถุโปร่งใส และสะท้อนจากวัตถุทึบแสงได้เมื่อแสงเข้าสู่ตาทำให้เกิดความรู้สึกในการมองเห็น

– คริสเตียน ฮอยเกนส์ (Christiaan Huygens) ได้ตั้งทฤษฎีเกี่ยวกับแสงว่าแสงเป็นคล่ืนสามารถนำไปใช้อธิบายการสะท้อน และการหักเหของแสง แต่ไม่สามารถแสดงว่าแสงมีการเล้ียวเบนได้ ทฤษฎีคล่ืนแสงจึงไม่เป็นที่ยอมรับ

– ค.ศ. 1801 ธอมัส ยัง (Thomas Young) ได้ทำการทดลองเกี่ยวกับการแทรกสอดและการเล้ียวเบนของแสงและสามารถวัดความยาวของคล่ืนแสงได้ทำให้ทฤษฎีที่ว่าแสงเป็นอนุภาคของนิวตันหมดไป

– ค.ศ. 1865 เจมส์ เคลิร์ก แมกซ์เวลล์ (James Clerk Maxwell) ได้แสดงให้เห็นว่าเมื่อประจุไฟฟ้าเคล่ือนที่แบบ
ซิมเปิลฮาร์โมนิกจะแผ่คล่ืนแม่เหล็กไฟฟ้าออกมา และอัตราเร็วของคล่ืนแม่เหล็กไฟฟ้ามีค่าใกล้เคียงกับ อัตราเร็วของแสงจึงเป็นการสนับสนุนว่าแสงเป็นคล่ืนแม่เหล็กไฟฟ้า

– ค.ศ. 1905 อัลเบิร์ต ไอน์สไตน์ (Albert Einstein) ได้เสนอว่าแสงเป็นอนุภาค ซึ่งอนุภาคของแสงก็คือกลุ่มก้อนของพลังงานที่เรียกว่า โฟตอน (Photon) และพลังงานของโฟตอนขึ้นอยู่กับค่าความถี่ของแสง ซึ่งแตกตางจากทฤษฎีของนิวตัน

– ปัจจุบัน – ทฤษฎีควอนตัมอธิบายว่าแสงมีลักษณะเป็นทั้งคล่ืนและอนุภาค ขึ้นอยู่กับการสังเกตและสถานการณ์ที่เกิดขึ้น

ภาพนักวิทยาศาสตร์คนสำคัญที่ศึกษาเกี่ยวกับแสง - แสงเชิงคลื่น

นักวิทยาศาสตร์ได้พิสูจน์แล้วว่า “แสง” ไม่ได้เดินทางเป็นเพียงเส้นตรงธรรมดา แต่มีพฤติกรรมคล้ายคล่ืน ในบทความนี้เราจะพูดถึงคุณสมบัติของแสงที่แสดงให้เห็นว่าเป็นคล่ืน ผ่านปรากฏการณ์การแทรกสอดและการเล้ียวเบน โดยการใช้อุปกรณ์ 3 ประเภท ได้แก่ สลิตเดี่ยว สลิตคู่ และเกรตติง

การแทรกสอดของแสงผ่านสลิตคู่

สลิตคู่ (double slit) คืออุปกรณ์ทางแสงที่ประกอบด้วยช่องเปิดขนาดเล็กสองช่อง ซึ่งมีความกว้างใกล้เคียงกันและอยู่ใกล้กัน

การแทรกสอดของแสงผ่านสลิตคู่ เป็นปรากฏการณ์ที่เกิดขึ้นเมื่อแสงเดินทางผ่านช่องเปิดสองช่อง แล้วเกิดการซ้อนทับของคล่ืนแสง ทำให้เกิดลวดลายแทรกสอดบนฉากรับภาพ ซึ่งปรากฏเป็นแถบสว่างและแถบมืด

แถบสว่าง → เกิดจากการแทรกสอดเสริม (สันคล่ืนรวมกับสันคล่ืน, ท้องคลื่นรวมกับท้องคล่ืน)
แถบมืด → เกิดจากการแทรกสอดหักล้าง (สันคล่ืนรวมกับท้องคล่ืน)

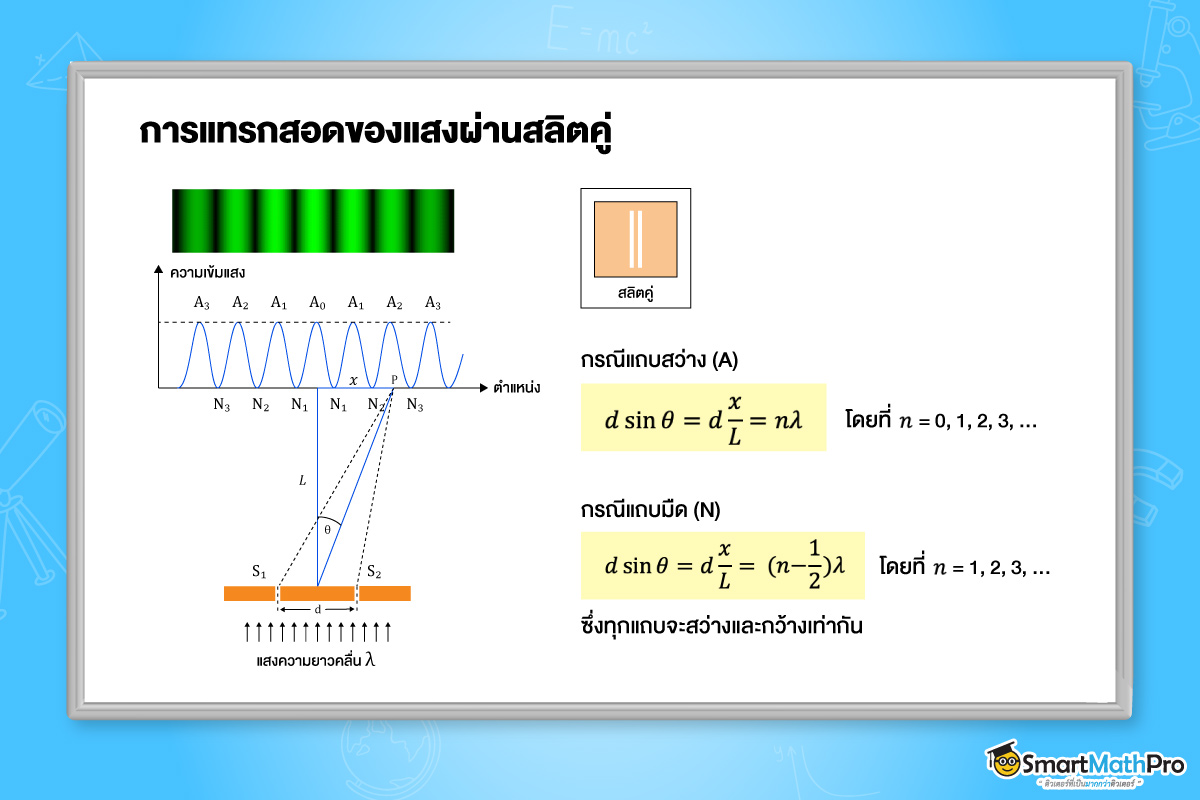
โดยที่ $d=$ ระยะห่างระหว่างสลิตคู่

$\lambda =$ ความยาวคล่ืนของแสง

$n=$ ลำดับการแทรกสอด

$\theta =$ มุมที่แถบแสงปรากฏ

ตัวอย่าง : การแทรกสอดของแสงผ่านสลิตคู่

เมื่อฉายแสงความยาวคล่ืน $500$ นาโนเมตร ลงบนสลิตคู่ ซึ่งมีระยะห่างระหว่างสลิตเป็น $1$ ไมโครเมตร อยากทราบว่าจุดที่เกิดการแทรกสอดแบบเสริมกันจุดที่ $1$ จะเบนจากแนวที่ฉายแสงเป็นมุมเท่าใด

จากสมการ $d\sin\theta =n\lambda$

จะได้ $\left ( 1\times 10^{-6} \right )\sin\theta =1\left ( 500\times 10^{-9} \right )$

$\sin\theta =\frac{1\left ( 500\times 10^{-9} \right )}{1\times 10^{-6}}$

$\sin\theta =0.5$

$\theta =30^{\circ}$

ตอบ จุดที่เกิดการแทรกสอดแบบเสริมกันจุดที่ $1$ จะเบนจากแนวที่ฉายแสงเป็นมุม $30^{\circ}$

การเล้ียวเบนของแสงผ่านสลิตเดี่ยว

สลิตเดี่ยว (Single Slit) คืออุปกรณ์ทางแสงที่ประกอบด้วยช่องเปิดช่องเดียว ซึ่งมีความกว้างน้อย ๆ ค่าหนึ่ง

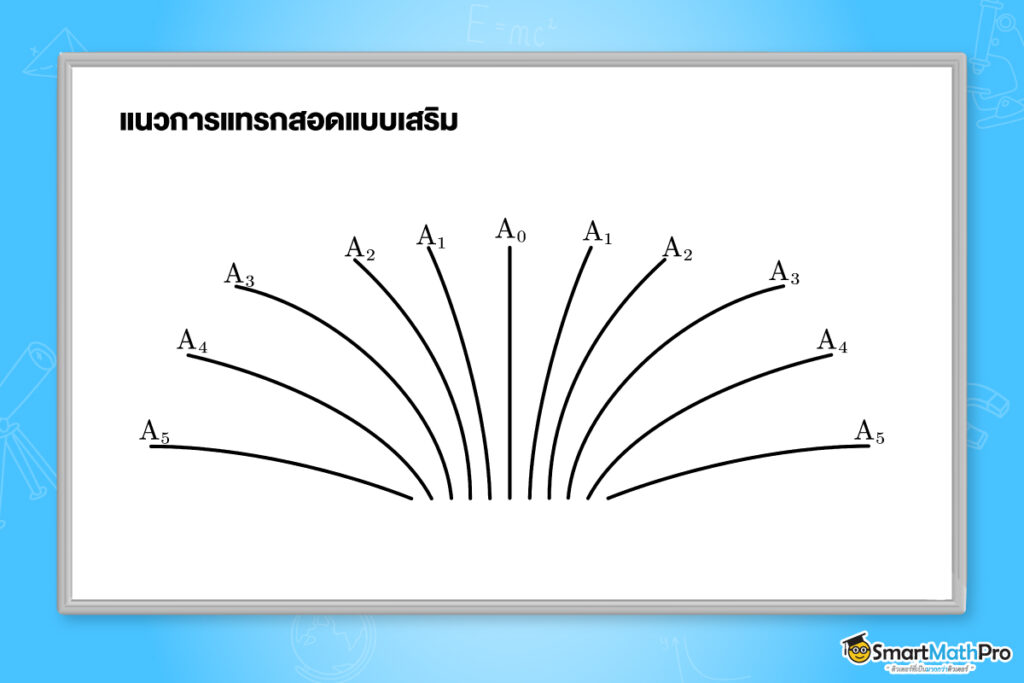
เมื่อแสงเคล่ือนที่ผ่านสลิตเดี่ยวแคบ ๆ ที่มีขนาดเทียบเท่ากับความยาวคล่ืนแสง แสงจะเกิดปรากฏการณ์เล้ียวเบน โดยขอบของสิ่งกีดขวางจะประพฤติตัวเสมือนแหล่งกำเนิดคล่ืนใหม่จำนวนมากมาย (ตามหลักของฮอยเกนส์) เมื่อนำฉากมารับจะเห็นริ้วมืดสว่างที่เกิดจากการแทรกสอดของคล่ืนจำนวนมากเหล่านี้ เกิดเป็นแถบมืดและแถบสว่างขึ้น

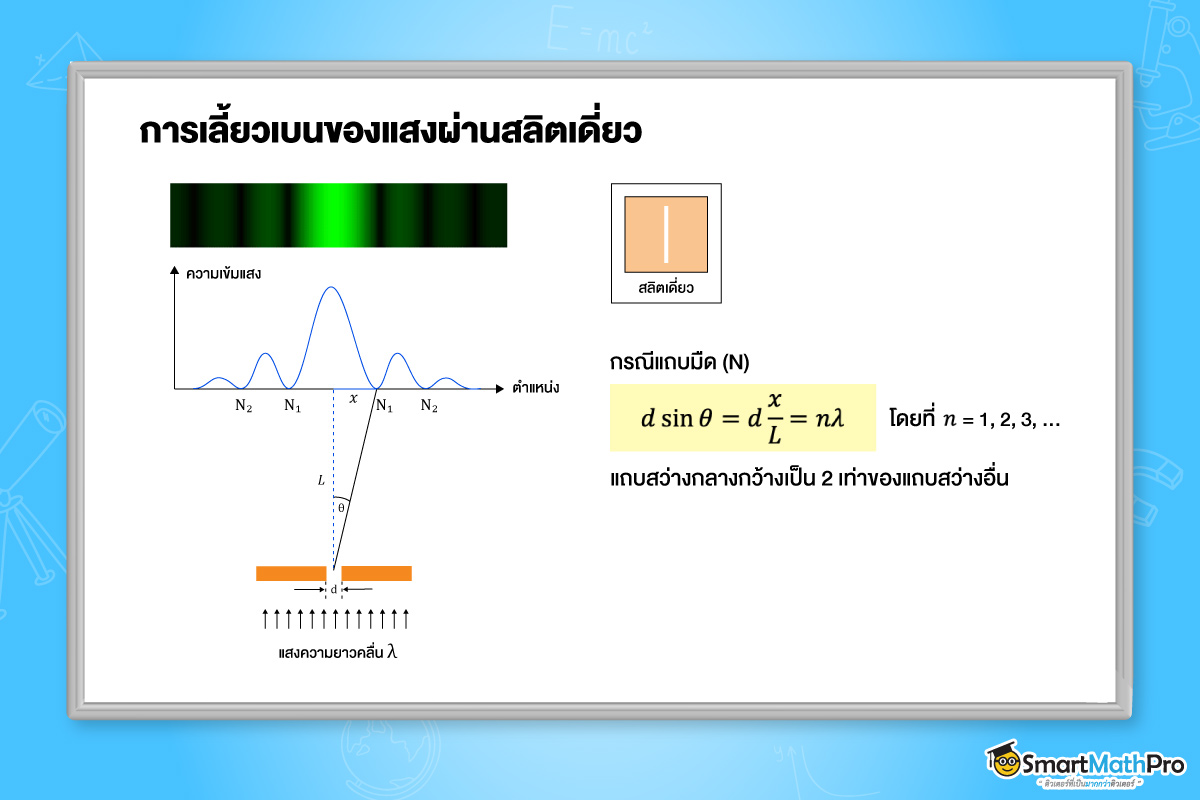
โดยที่ $d=$ ความกว้างของสลิตเดี่ยว
$\lambda =$ ความยาวคล่ืนของแสง
$n=$ ลำดับการแทรกสอด
$\theta =$ มุมของตำแหน่งที่เกิดแถบมืด

แถบสว่างกลางจะมีความกว้างและความสว่างมากที่สุด โดยแถบสว่างกลางมีความสัมพันธ์กับความกว้างของสลิต ดังนี้

เมื่อเพิ่มความกว้างของสลิต ความกว้างของแถบสว่างกลางจะแคบลง
เมื่อลดความกว้างของสลิตลง ความกว้างของแถบกลางจะเพิ่มขึ้น

ตัวอย่าง : การเล้ียวเบนของแสงผ่านสลิตเดี่ยว

เมื่อให้แสงมีความยาวคล่ืน $600$ นาโนเมตร ผ่านช่องแคบเดี่ยว และต้องการให้แถบมืดแรกเบนจากแนวกลาง $30^{\circ}$ จงหาความกว้างของช่องแคบนี้

วิธีทำ : จากสมการ $d\sin\theta =n\lambda$

จะได้ $d\sin30^{\circ}=1\left ( 600\times 10^{-9} \right )$

$d\left ( \frac{1}{2} \right )=1\left ( 600\times 10^{-9} \right )$

$d=2\left ( 600\times 10^{-9} \right )$

$d=1.2\times 10^{-6}m$

$d=1.2\mu m$

ตอบ ความกว้างของช่องแคบนี้มีค่าเท่ากับ $1.2\mu m$

การเล้ียวเบนของแสงผ่านเกรตติง

เกรตติง (Grating) เป็นอุปกรณ์ที่ใช้สำหรับวิเคราะห์สเปกตรัมของแสงและวัดความยาวคล่ืนของแสง โดยอาศัยหลักการเล้ียวเบนและการแทรกสอดของคล่ืน โครงสร้างของเกรตติงเป็นแผ่นวัตถุโปร่งใสผิวเรียบที่มีช่องเปิดเล็ก ๆ เรียงตัวขนานกันอย่างหนาแน่น โดยทั่วไปอาจมีตั้งแต่ $100$ ถึง $10,000$ ช่องต่อเซนติเมตร

เมื่อแสงจากแหล่งกำเนิดต่าง ๆ เช่น ดวงอาทิตย์หรือแสงขาวหลอดไฟฉาย ผ่านเข้าสู่เกรตติง จะเกิดการกระจายตัวออกเป็นสเปกตรัมสีต่าง ๆ อย่างชัดเจน กระบวนการนี้พัฒนามาจากแนวคิดเริ่มแรกของสลิตคู่ โดยการเพิ่มจำนวนและลดระยะห่างระหว่างช่องเปิด ส่งผลให้การเล้ียวเบนของแสงมีความละเอียดและสมบูรณ์มากยิ่งขึ้น ทำให้เราสามารถสังเกตเห็นองค์ประกอบของแสงขาวได้อย่างเป็นระบบ

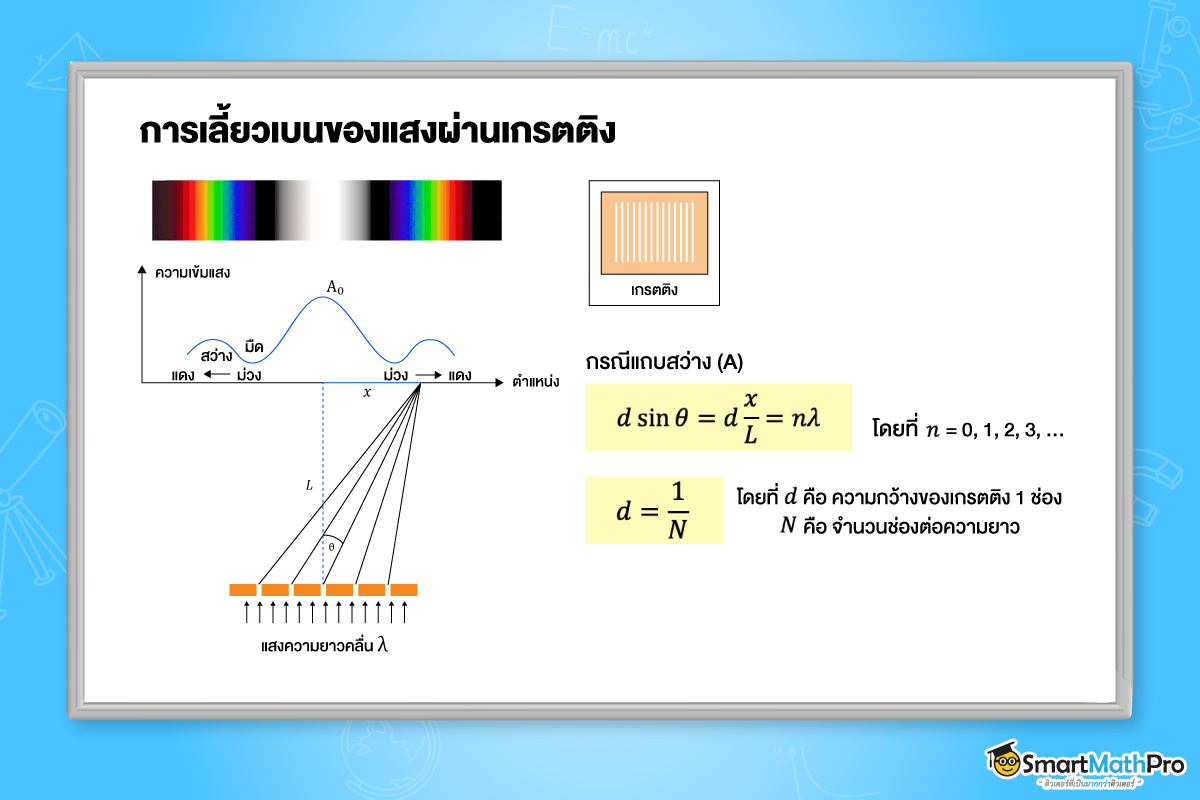
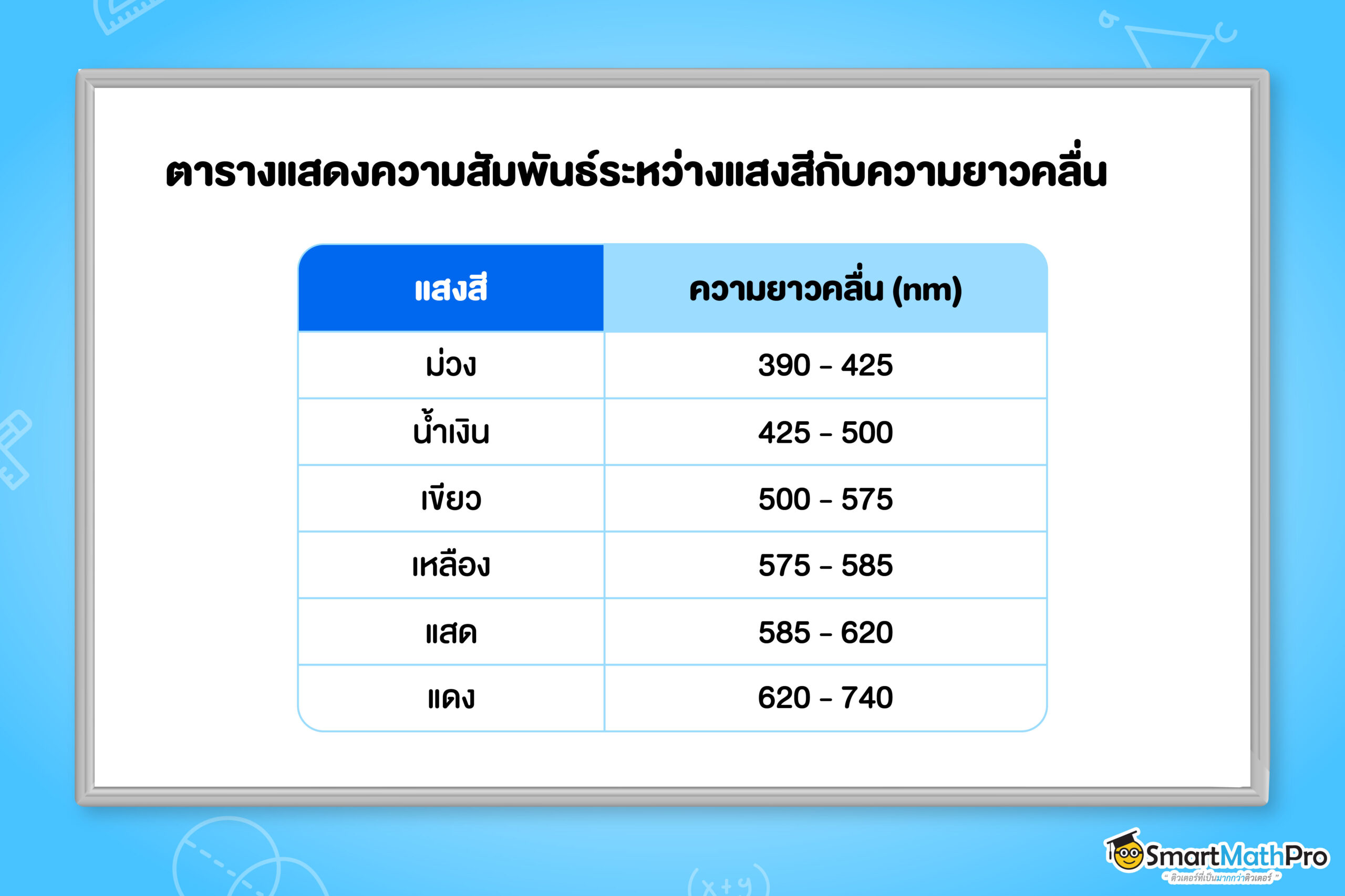
แสงที่เบนจากแนวกลางมากที่สุดคือ แสงสีแดง และแสงที่เบนจากแนวกลางน้อยที่สุดคือ แสงสีม่วง ซึ่งสอดคล้องกับสมการ $d\sin\theta =n\lambda$ โดยแสงสีต่าง ๆ มีความยาวคล่ืน ดังแสดงในตาราง

ตัวอย่าง : การเล้ียวเบนของแสงผ่านเกรตติง

เกรตติง $10,000$ เส้นต่อเซนติเมตร ถ้าฉายแสงความยาวคลื่ืน $\lambda$ ตกตั้งฉากกับเกรตติง แถบสว่างที่เกิดขึ้นแถบแรกบนจอ จะอยู่ห่างจากแนวกลางเป็นมุม $30^{\circ}$ ค่า $\lambda$ มีค่าเท่าใด

วิธีทำ
จากสมการ $d\sin\theta =n\lambda$

จะได้ $\frac{1}{N}\sin30^{\circ}=1\left( \lambda \right)$

$\lambda =\frac{1}{10^{6}}\times \frac{1}{2}$

$\lambda=5\times 10^{-7}m$

$\lambda=500nm$

ตอบ ความยาวคล่ืนมีค่าเท่ากับ $500nm$

สรุปสูตรเกี่ยวกับแสงเชิงคล่ืน

ติว A-Level ฟิสิกส์กับ SmartMathPro

พี่ขอแนะนำตัวช่วยอย่าง คอร์สเตรียมสอบมหาลัยฯ ของ SmartMathPro เลยย มีให้เลือกมากมายทั้งสนาม TGAT / TPAT หรือ A-Level และสอนโดยติวเตอร์ที่มีความเชี่ยวชาญในแต่ละวิชาด้วยไม่ว่าจะเป็น พี่ปั้น, อ.ขลุ่ย, พี่หมออู๋,
ครูกอล์ฟ, พี่ลัคกี้, พี่เกม GAT ENG COOL COOL, พี่ฟาร์ม

โดยในแต่ละคอร์สจะสอนปูพื้นฐานแบบละเอียด อิงตาม Test Blueprint ปีล่าสุด (ใครที่พื้นฐานไม่แน่นก็สามารถเรียนได้) พร้อมพาตะลุยโจทย์แบบไต่ระดับ ตั้งแต่โจทย์ซ้อมมือไปจนถึงข้อสอบเก่าหรือโจทย์ที่ใกล้เคียงกับข้อสอบจริง แถมยังแจกเทคนิคในการทำข้อสอบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้นและช่วยเพิ่มโอกาสในการอัปคะแนนให้อีกด้วย สำหรับน้อง ๆ คนไหนที่สมัครตอนนี้ รับฟรี Unseen Mock Test ชุดพิเศษ และสิทธิพิเศษต่าง ๆ ประจำเดือน ถ้าใครสนใจ คลิก เข้ามาดูรายละเอียดแต่ละคอร์สได้เลยยย

ตัวอย่างข้อสอบเรื่องแสงเชิงคล่ืน

เฉลยตัวอย่างแนวข้อสอบฟิสิกส์ (แสงเชิงคล่ืน)

วิธีทำ
ขั้นตอนที่ $1$ คำนวณหา $\lambda _{1}$

จากสมการ $d\sin\theta=\left(n-\frac{1}{2}\right)\lambda$

จะได้ $d\sin\theta=\left(3-\frac{1}{2}\right)\lambda_{1}$ ; แถบมืดอันดับที่ $3(n=3)$

ขั้นตอนที่ $2$ คำนวณหา $\lambda _{2}$

จากสมการ $d\sin\theta=n\lambda$

จะได้ $d\sin\theta =2\lambda_{2}$ ; แถบสว่างอันดับที่ $2(n=2)$

ขั้นตอนที่ $3$ คำนวณหา อัตราส่วนระหว่าง $\lambda _{1}$ และ $\lambda _{2}$

เนื่องจาก แถบมืดอันดับที่ $3$ ของแสง $\lambda _{1}$ เกิดที่เดียวกับแถบสว่างอันดับที่ $2$ ของแสง $\lambda _{2}$

จะได้ $\left ( 3-\frac{1}{2} \right )\lambda _{1}=2\lambda _{2}$

$2.5\lambda _{1}=2\lambda _{2}$

จะได้ $\frac{\lambda_{1}}{\lambda_{2}}=\frac{2}{2.5}=\frac{4}{5}$

ตอบ อัตราส่วนระหว่าง $\lambda _{1}$ และ $\lambda _{2}$ เป็น $4:5$

เฉลยตัวอย่างแนวข้อสอบฟิสิกส์ (แสงเชิงคล่ืน)

วิธีทำ
ขั้นตอนที่ $1$ คำนวณหา $d$
จากสมการ $d=\frac{1}{N}$

เนื่องจาก $N=2,500$ ช่องต่อเซนติเมตร $=\frac{2,500}{10^{-2}}$ ช่องต่อเมตร
จะได้ $d=\frac{10^{-2}}{2,500}$

ขั้นตอนที่ $2$ คำนวณหา $n$
จากสมการ $d\sin\theta =n\lambda$

จะได้ $\frac{10^{-2}}{2,500}\sin90^{\circ}=n(720\times10^{-9})$

$n=\frac{10^{-2}}{2,500}\times \frac{1}{720\times 10^{-9}}=5.56$

$^{\ast }$ แถบสว่างสุดท้ายที่จะสามารถเห็นได้คือ แถบสว่างที่ $5(n=5)^{\ast }$

ขั้นตอนที่ $3$ คำนวณหา แถบสว่างบนฉากรับทั้งหมด

แถบสว่างบนฉากรับทั้งหมด $2n+1=2(5)+1=11$

แนวการแทรกสอดแบบเสริม แสงเชิงคลื่น

แถบสว่างที่เกิดขึ้นบนฉาก

ตอบ ข้อ 5. $11$

เป็นอย่างไรกันบ้างกับ “สรุปเนื้อหาเรื่อง แสงเชิงคล่ืน ฟิสิกส์ ม.5” และแนวข้อสอบที่พี่นำมาฝากในวันนี้ แนะนำว่าถ้าใครอยากจะแม่นเนื้อหาเรื่องนี้ นอกจากก็อ่านเนื้อหาแล้ว ก็ควรฝึกทำแบบฝึกหัดหรือข้อสอบเก่าบ่อย ๆ ด้วยน้า