การแปลงทางเรขาคณิตเป็นเนื้อหาที่น้อง ๆ ส่วนใหญ่จะได้เจอใน ม.2 เทอม 1 ซึ่งน้อง ๆ จะได้เรียนเกี่ยวกับรูปที่เกิดจากการเลื่อนขนาน การสะท้อน และการหมุน
โดยในบทความนี้ พี่จะพาน้อง ๆ ไปรู้จักการแปลงทางเรขาคณิตให้มากยิ่งขึ้น ทั้งเรื่องความหมาย, สมบัติ, ตัวอย่างโจทย์ และแบบฝึกหัดให้น้อง ๆ ได้ลองทำกัน ถ้าใครพร้อมแล้ว ก็ไปลุยกันเลยย
การแปลงในทางคณิตศาสตร์ หมายถึง การเปลี่ยนแปลงของวัตถุโดยอาจมีการเปลี่ยนแปลงขนาด รูปร่าง หรือตำแหน่งของวัตถุ โดยการแปลงที่น้อง ๆ เคยเห็นในชีวิตประจำวันมีเยอะเลย เช่น การยืนบนบันไดเลื่อน ซึ่งตัวเราจะขยับเลื่อนขึ้นหรือลงไปตามบันได การมองภาพสะท้อนของตัวเองในกระจกเงา การหมุนของเข็มนาฬิกา
หัวใจของการแปลงที่น้อง ๆ ควรรู้ คือจุดทุกจุดของรูปในตำแหน่งเดิม (หรือขนาดเดิม) จะต้องส่งไปยังรูปที่ตำแหน่งใหม่ (หรือขนาดใหม่) แบบจุดต่อจุด โดยในทางเรขาคณิตก็มีการแปลงที่กล่าวถึงความเกี่ยวข้องกันระหว่างรูปเรขาคณิตเช่นกัน
โดยเราจะเรียกรูปเรขาคณิตก่อนการแปลงว่า รูปต้นแบบ (Pre – image) เรียกรูปเรขาคณิตหลังการแปลงว่า รูปที่ได้จากการแปลง (Image) และเรียกการเปลี่ยนแปลงนั้นว่า การแปลงทางเรขาคณิต (Geometric transformation)
ซึ่งในบทนี้ จะพูดถึงการแปลงทางเรขาคณิตเพียง 3 แบบ คือ การเลื่อนขนาน (Translation), การสะท้อน (Reflection) และการหมุน (Rotation) เท่านั้น โดยการแปลงทั้ง 3 แบบนี้จะทำให้รูปต้นแบบและรูปที่ได้จากการแปลงมีรูปร่างที่เหมือนกันและมีขนาดที่เท่ากันเสมอนั่นเอง
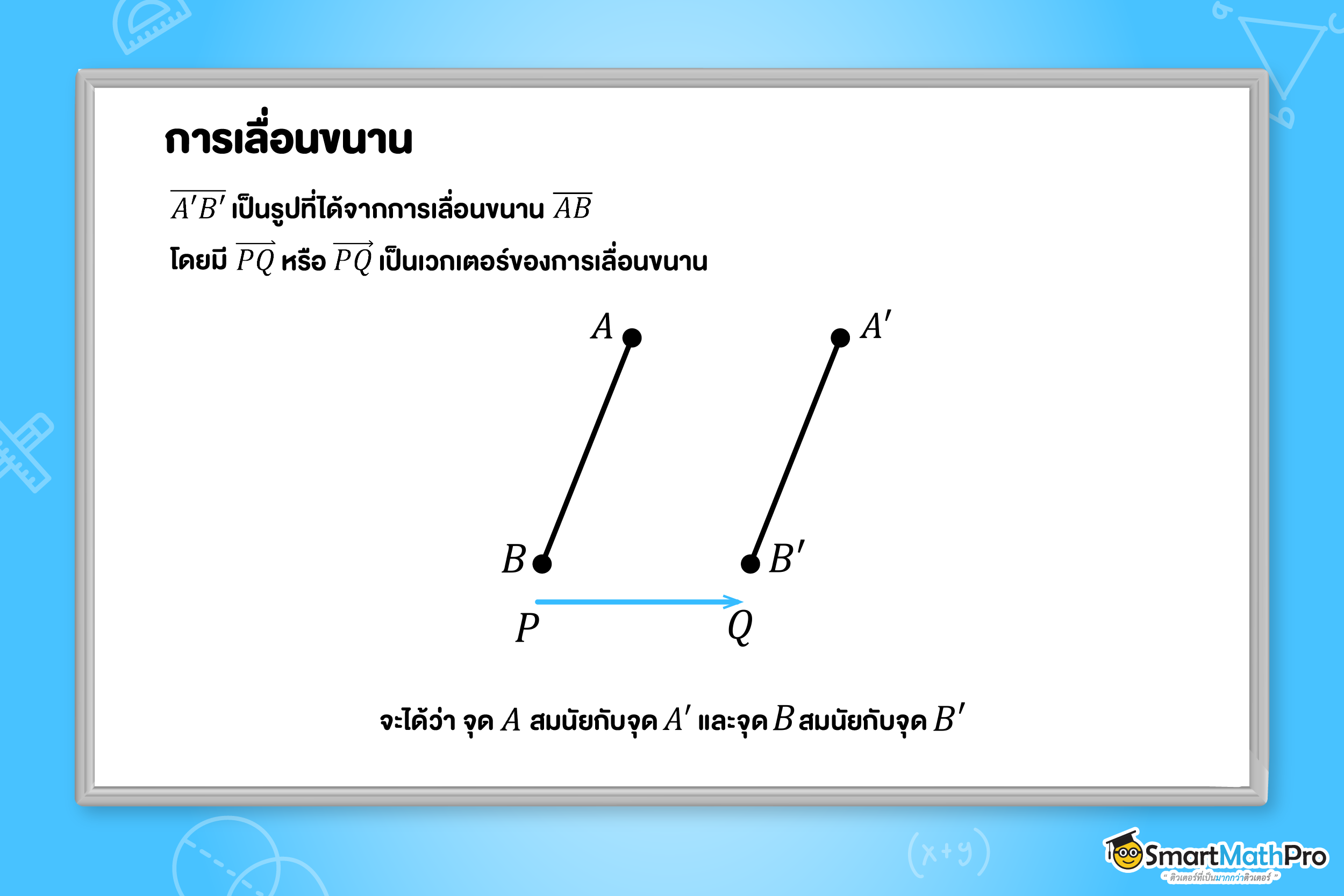
การเลื่อนขนาน
การเลื่อนขนาน คืออะไร ?
การเลื่อนขนานบนระนาบ เป็นการแปลงทางเรขาคณิตที่มีการเลื่อนจุดทุกจุดไปบนระนาบตามแนวเส้นตรงในทิศทาง
เดียวกัน และเป็นระยะทางเท่ากันตามที่กำหนด
สมบัติของการเลื่อนขนาน
- รูปต้นแบบและรูปที่ได้จากการเลื่อนขนานสามารถทับกันได้สนิทโดยไม่ต้องพลิกรูป ซึ่งกล่าวได้ว่า รูปต้นแบบและรูปที่ได้จากการเลื่อนขนานเท่ากันทุกประการ
- ส่วนของเส้นตรงที่เชื่อมระหว่างจุดที่สมนัยกันแต่ละคู่ จะขนานกันและยาวเท่ากันทุกเส้น
- ส่วนของเส้นตรงบนรูปต้นแบบและรูปที่ได้จากการเลื่อนขนานส่วนของเส้นตรงนั้น จะขนานกันและยาวเท่ากัน
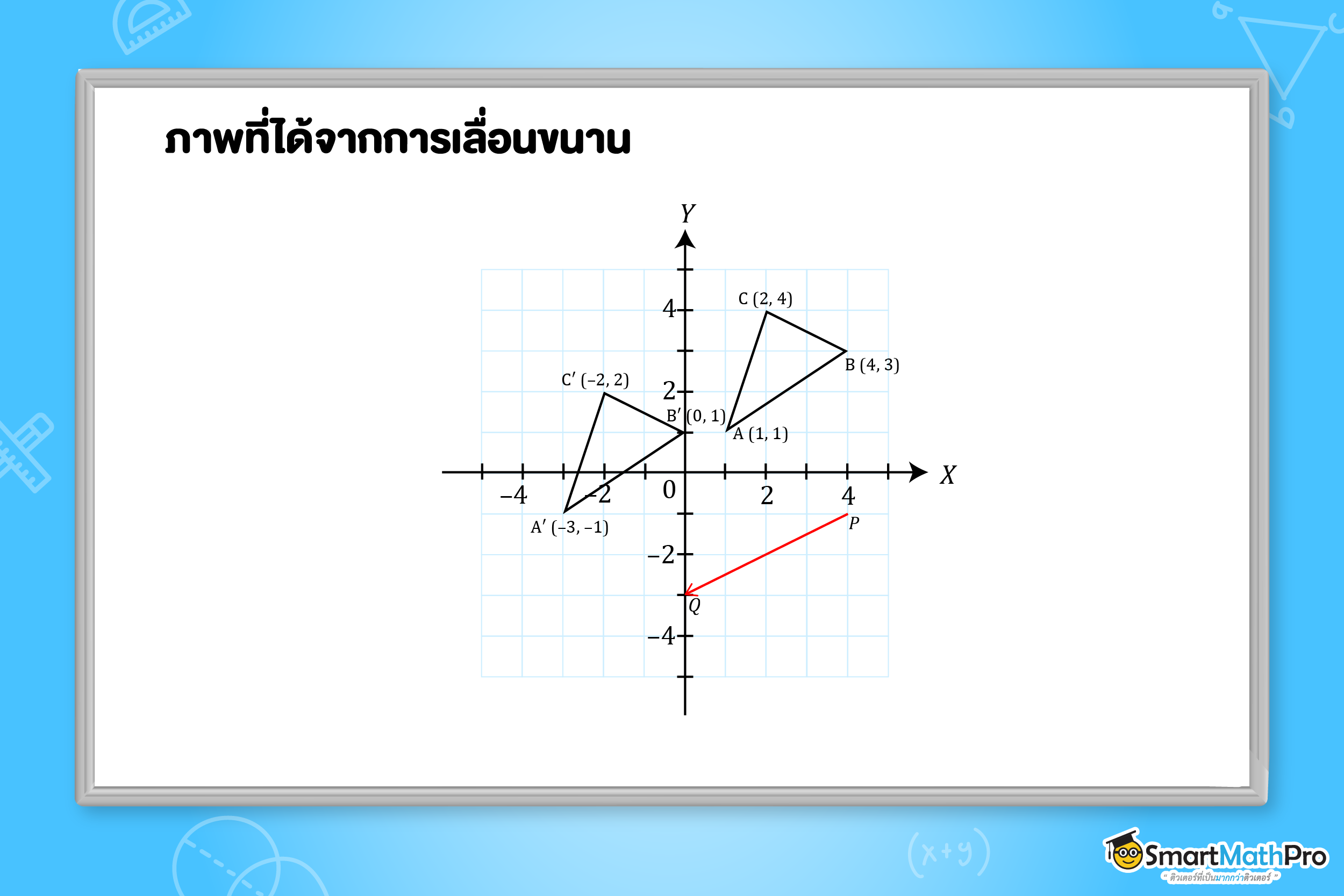
ตัวอย่างที่ 1 จงหาจุดยอดของ \bigtriangleup A^{\prime}B^{\prime}C^{\prime} ซึ่งเป็นรูปที่ได้จากการเลื่อนขนาน \bigtriangleup ABC ด้วย \overrightarrow{PQ} ที่กำหนด

วิธีทำ ภาพที่ได้จากการเลื่อนขนานมีลักษณะดังนี้
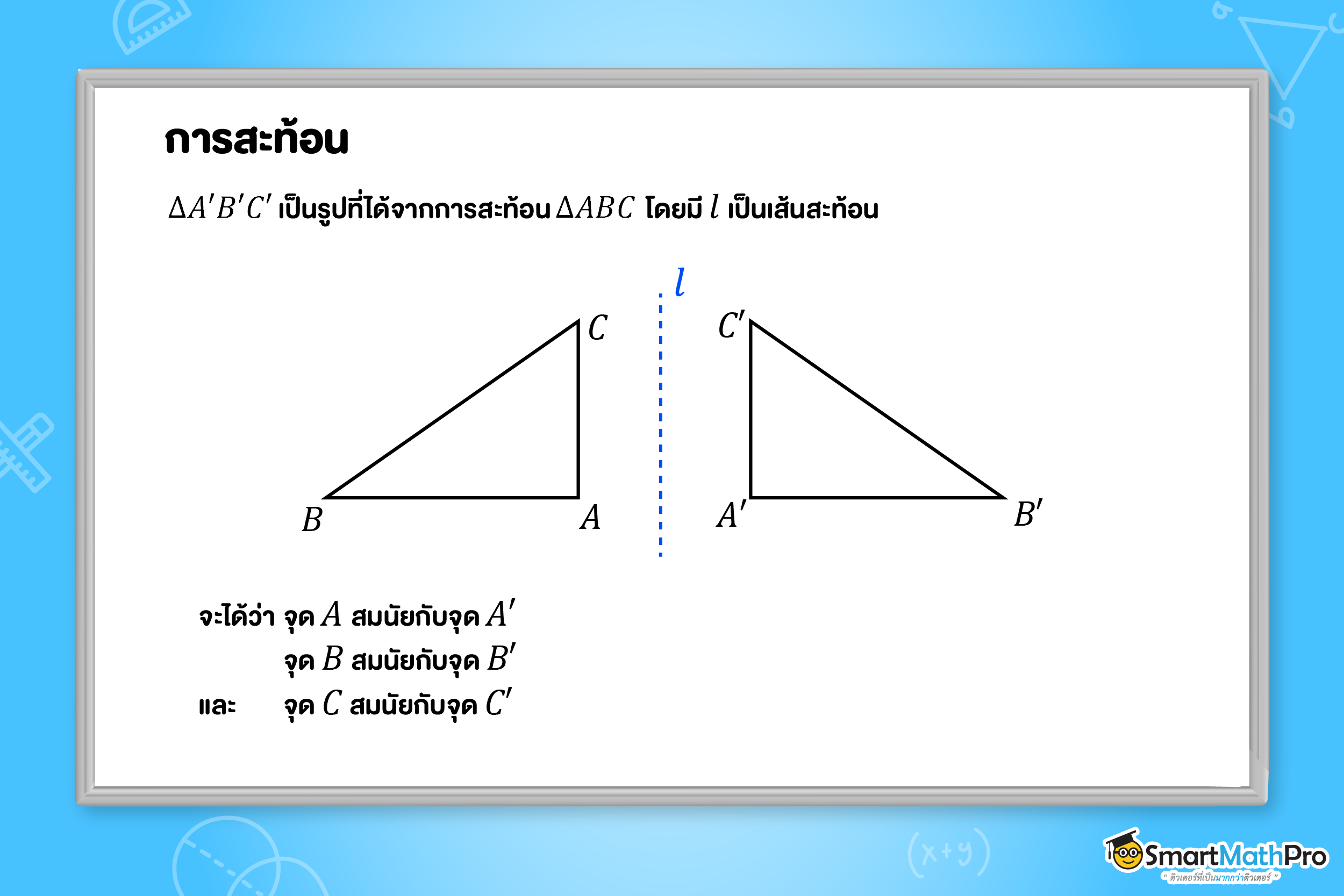
การสะท้อน
การสะท้อน คืออะไร ?
การสะท้อนบนระนาบ เป็นการแปลงทางเรขาคณิตที่มีการพลิกรูป โดยจะมีเส้นตรงเส้นหนึ่งเป็น เส้นสะท้อน
(Line of reflection หรือ Mirror line)
สมบัติของการสะท้อน
- รูปต้นแบบและรูปที่ได้จากการสะท้อน สามารถทับกันได้สนิทโดยต้องพลิกรูปต้นแบบหรือพลิกรูปที่ได้จากการสะท้อนอย่างหนึ่งอย่างใด ซึ่งกล่าวได้ว่า รูปต้นแบบและรูปที่ได้จากการสะท้อนเท่ากันทุกประการ
- จุดที่สมนัยกันแต่ละคู่จะอยู่ห่างจากเส้นสะท้อนเท่ากัน หรือเส้นสะท้อนจะแบ่งครึ่งและตั้งฉากกับส่วนของ
เส้นตรงที่เชื่อมระหว่างจุดที่สมนัยกันบนรูปต้นแบบและรูปที่ได้จากการสะท้อน - ส่วนของเส้นตรงที่เชื่อมระหว่างจุดที่สมนัยกันบนรูปต้นแบบและรูปที่ได้จากการสะท้อนทุกเส้นจะขนานกัน
ตัวอย่างที่ 2 จงหาจุดยอดของ \bigtriangleup A^{\prime}B^{\prime}C^{\prime} ซึ่งเป็นรูปที่ได้จากการสะท้อน \bigtriangleup ABC ด้วยแกน X
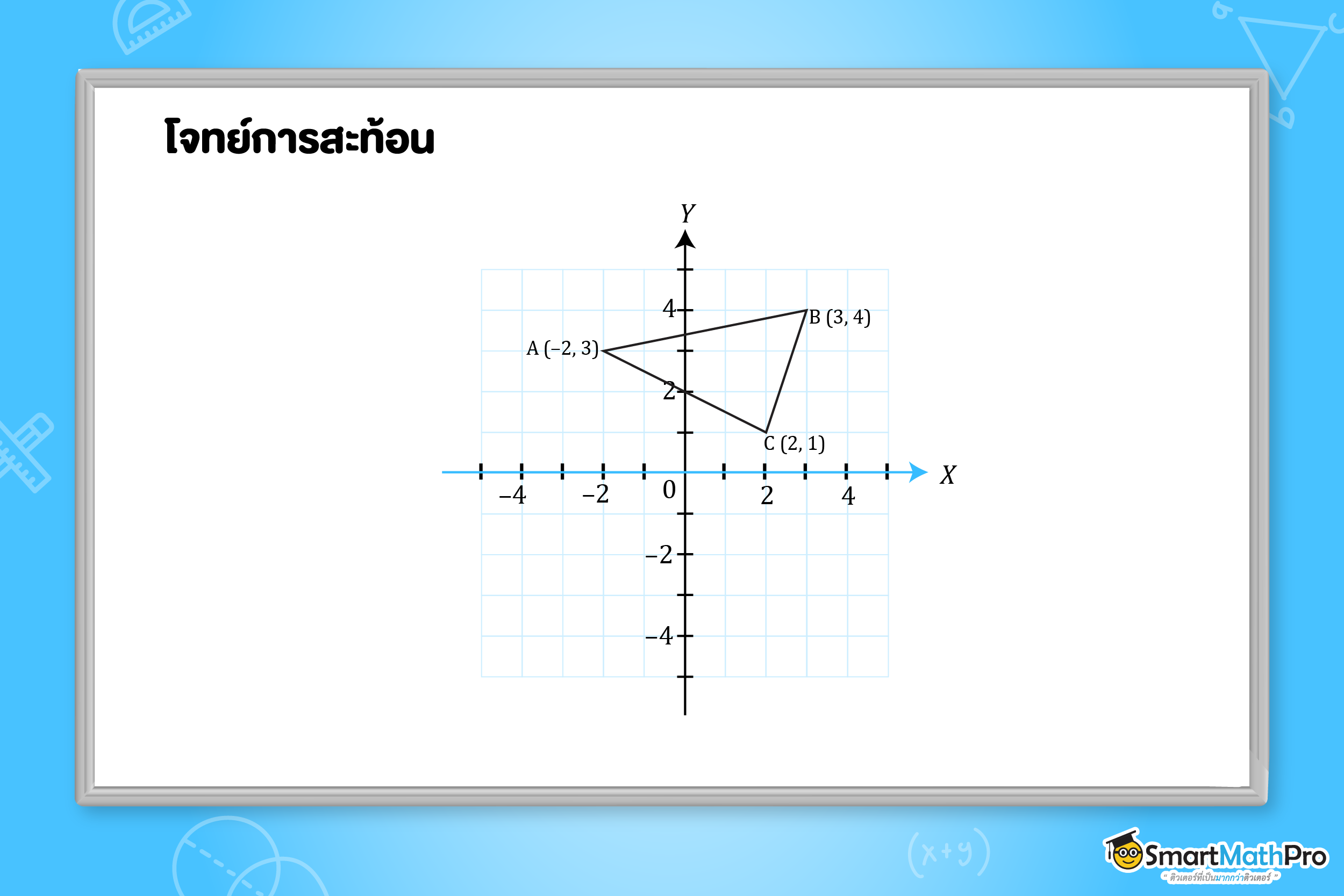
วิธีทำ ภาพที่ได้จากการสะท้อนมีลักษณะดังนี้
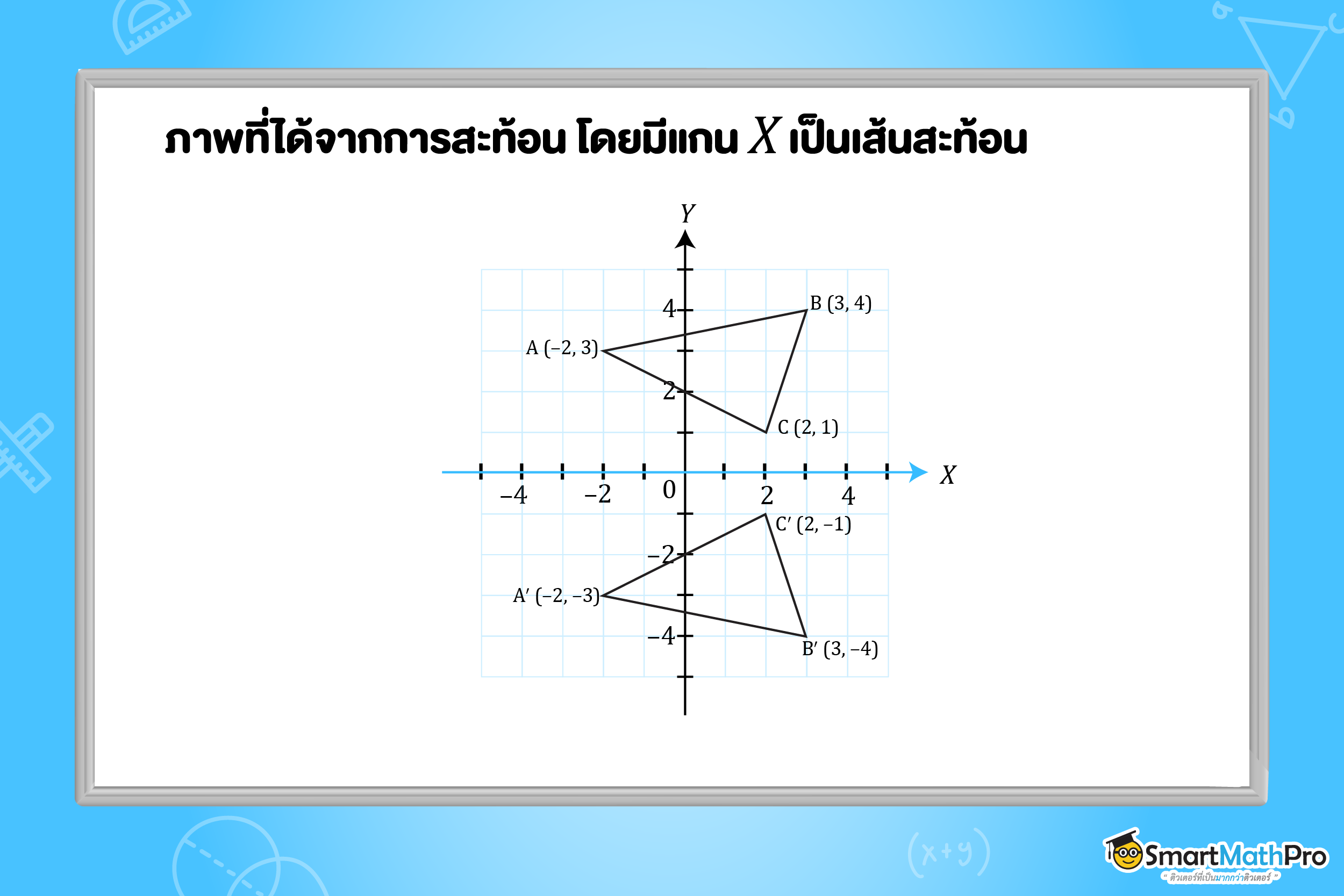
ตัวอย่างที่ 3 จงหาจุดยอดของ \bigtriangleup A^{\prime}B^{\prime}C^{\prime} ซึ่งเป็นรูปที่ได้จากการสะท้อน \bigtriangleup ABC ด้วยแกน Y
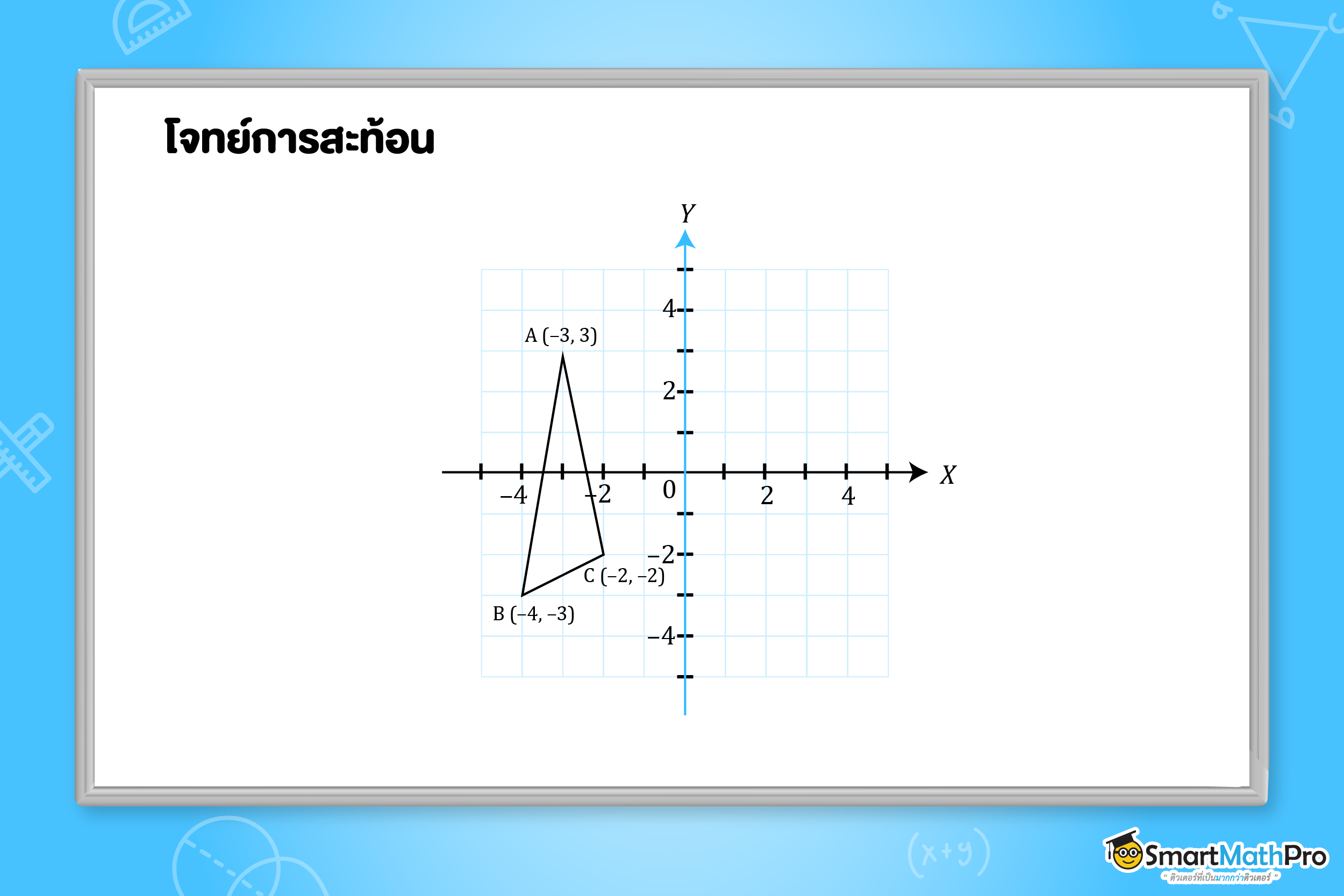
วิธีทำ ภาพที่ได้จากการสะท้อนมีลักษณะดังนี้

การหมุน
การหมุน คืออะไร ?
การหมุนบนระนาบ คือการแปลงทางเรขาคณิตที่มีจุด O เป็นจุดตรึง แล้วหมุนจุด P ไปบนระนาบ โดยจุด P^{\prime} เป็นรูปที่ได้จากการหมุนจุด P รอบจุด O ตามทิศทางที่กำหนด และจะเรียกจุด O ว่า จุดหมุน หรือ จุดศูนย์กลางของ
การหมุน (Centre of rotation)
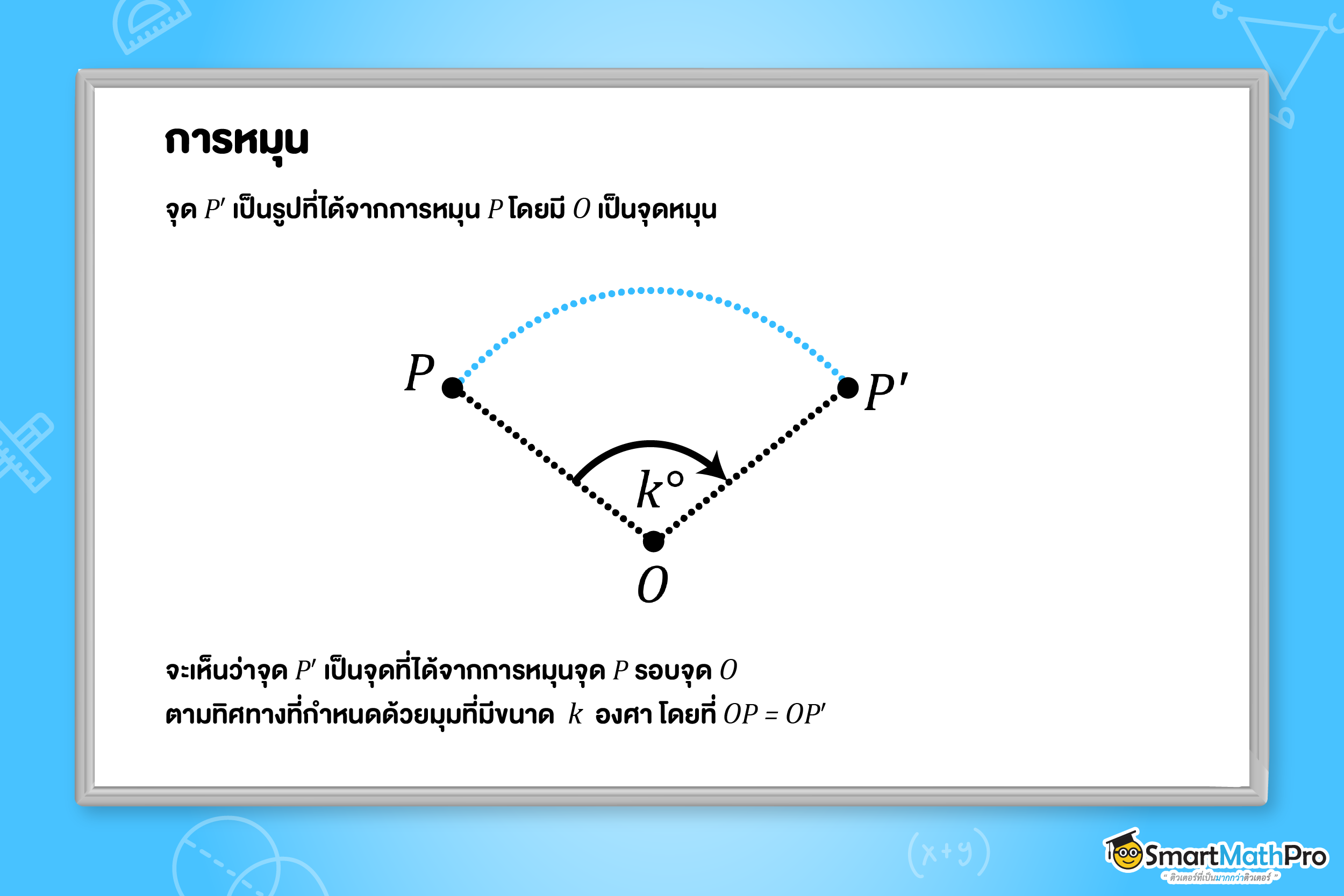
สมบัติของการหมุน
- รูปต้นแบบและรูปที่ได้จากการหมุน สามารถทับกันได้สนิทโดยไม่ต้องพลิกรูป ซึ่งกล่าวได้ว่ารูปต้นแบบและ
รูปที่ได้จากการหมุนเท่ากันทุกประการ - จุดแต่ละจุดบนรูปต้นแบบและรูปที่ได้จากการหมุนจุดนั้น จะอยู่บนวงกลมเดียวกันที่มีจุดหมุนเป็น
จุดศูนย์กลางของวงกลม แต่วงกลมทั้งหลายไม่จำเป็นต้องมีรัศมียาวเท่ากัน - เส้นตรงที่แบ่งครึ่งและตั้งฉากกับส่วนของเส้นตรงที่เชื่อมระหว่างจุดบนรูปต้นแบบและรูปที่ได้จากการหมุน
จุดนั้น จะผ่านจุดหมุนเสมอ
ตัวอย่างที่ 4 จงหาพิกัดของจุด P^{\prime} ซึ่งเป็นจุดที่ได้จากการหมุนจุด P โดยมีจุด (0, 0) เป็นจุดหมุน โดยหมุนทวนเข็มนาฬิกาด้วยมุม 90^\circ
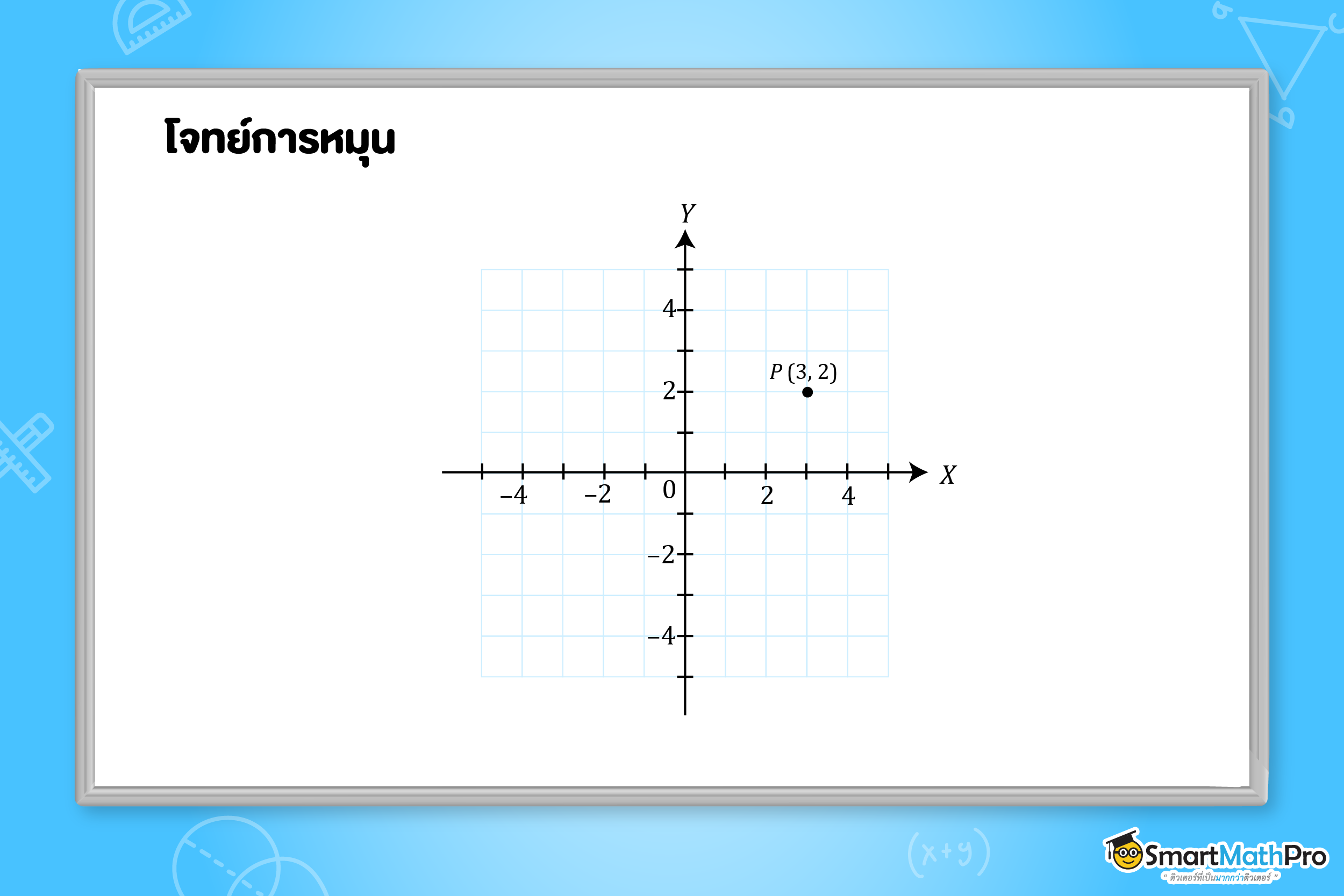
วิธีทำ จะได้ภาพที่ได้จากการหมุนมีลักษณะดังนี้

สรุปสูตรการแปลงทางเรขาคณิต

แบบฝึกหัดการแปลงทางเรขาคณิต
ตัวอย่างที่ 5 กำหนดให้ A^{\prime} คือจุดที่ได้จากการเลื่อนขนานจุด A(0, 4) ด้วย \overrightarrow{PQ} โดยมีเงื่อนไขดังนี้
- P(0, 0) และ Q(-2, 0)
- P(0, 0) และ Q(0, 3)
ข้อ 1 ตอบ A^{\prime}(-2, 4)
ข้อ 2 ตอบ A^{\prime}(0, 7)
ตัวอย่างที่ 6 กำหนดให้จุด A^{\prime} คือจุดที่ได้จากการสะท้อนจุด A(-1, 3) ด้วยเส้นสะท้อนที่กำหนดให้ต่อไปนี้
- แกน X
- แกน Y
- y=x
- y=-x
ข้อ 1 ตอบ A'(-1, -3)
ข้อ 2 ตอบ A^{\prime}(1, 3)
ข้อ 3 ตอบ A^{\prime}(3, -1)
ข้อ 4 ตอบ A^{\prime}(-3, 1)
ตัวอย่างที่ 7 กำหนดให้ A^{\prime} คือจุดที่ได้จากการหมุนจุด A(3, 2) โดยมีจุด (0, 0) เป็นจุดหมุน และมีเงื่อนไขในการหมุนดังนี้
- ตามเข็มนาฬิกาด้วยมุม 90^\circ
- ทวนเข็มนาฬิกาด้วยมุม 90^\circ
- ตามเข็มนาฬิกาด้วยมุม 180^\circ
- ทวนเข็มนาฬิกาด้วยมุม 180^\circ
ข้อ 1 ตอบ A^{\prime}(2, -3)
ข้อ 2 ตอบ A^{\prime}(-2, 3)
ข้อ 3 ตอบ A^{\prime}(-3, -2)
ข้อ 4 ตอบ A^{\prime}(-3, -2)
อ่านกันมาจนถึงตรงนี้ พี่คิดว่าน้อง ๆ น่าจะเข้าใจเรื่องการแปลงทางเรขาคณิต ม.2 กันมากขึ้นแล้ว โดยพี่แนะนำให้ฝึกทำโจทย์เรื่องนี้บ่อย ๆ เพราะจะช่วยให้แม่นยำในเนื้อหามากขึ้น ซึ่งนอกจากแบบฝึกหัดในบทความนี้แล้ว พี่ยังมีแบบฝึกหัดให้ลองทำเพิ่มเติมด้วยน้าา >> แบบฝึกหัดการแปลงทางเรขาคณิต ม.2
สำหรับน้อง ๆ ม.2 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์
พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.2 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน แนวข้อสอบเข้าม.4 และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก เลย
บทความ แนะนำ
บทความ แนะนำ

ทีมวิชาการคณิตศาสตร์
ผู้อยู่เบื้องหลังการจัดทำคอร์สเรียนร่วมกับพี่ติวเตอร์
และผู้เขียนบทความวิชาการคณิตศาสตร์ของสถาบัน SmartMathPro

ทีมวิชาการคณิตศาสตร์
ผู้อยู่เบื้องหลังการจัดทำคอร์สเรียนร่วมกับพี่ติวเตอร์
และผู้เขียนบทความวิชาการคณิตศาสตร์ของสถาบัน SmartMathPro
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro