
คณิตศาสตร์เป็นวิชาที่มีเนื้อหาและสูตรค่อนข้างเยอะมากก ทำให้บางครั้งน้อง ๆ ใช้สูตรคณิตผิดหรือลืมบางสูตรไปได้
พี่เลยทำสรุปสูตรคณิตศาสตร์ ม.ต้น ที่สำคัญมาให้ ไม่ว่าจะนำไปทบทวนความรู้หรือท่องก่อนสอบก็นำไปใช้ได้เลย
ถ้าพร้อมแล้ว ไปดูกันนน
สนใจหัวข้อไหน ... กดอ่านเลย
Toggleสูตรคณิตศาสตร์ ม.1
เลขยกกำลัง
ให้ a เป็นจำนวนจริงและ n เป็นจำนวนเต็มบวก
a^{n}=a \times a\times a\times \cdots \times a (a คูณกันทั้งหมดเป็นจำนวน n ตัว)
และ a เป็นจำนวนจริงใด ๆ ที่ไม่เท่ากับ 0
a^0=1 และ a^{-n}=\frac{1}{a^{n}}
สมบัติของเลขยกกำลัง
เมื่อ a เป็นจำนวนใด ๆ ที่ไม่เท่ากับ 0 และ m,n เป็นจำนวนเต็ม
- a^{-n}=\frac{1}{a^{n}}
- a^{m}\times a^{n} =a^{m+n}
- \frac{a^{m}}{a^{n}} =a^{m-n}
สัญกรวิทยาศาสตร์ (Scientific notation)
A \times10^{n} เมื่อ 1≤ A<10 และ n เป็นจำนวนเต็ม
ทศนิยมและเศษส่วน
การเปรียบเทียบเศษส่วนสามารถทำได้โดยทำส่วนให้เท่ากันก่อนเปรียบเทียบ
การบวกและลบเศษส่วน
- เศษส่วนที่มีส่วนเท่ากัน
- การบวก : \frac{a}{b}+\frac{c}{b}=\frac{a+c}{b} เมื่อ b\neq 0
- การลบ : \frac{a}{b}-\frac{c}{b}=\frac{a-c}{b} เมื่อ b\neq 0
- เศษส่วนที่มีส่วนไม่เท่ากัน
- การบวก : \frac{a}{b}+\frac{c}{d}=\frac{ad+cb}{bd} เมื่อ b, d\neq 0
- การลบ : \frac{a}{b}-\frac{c}{d}=\frac{ad-cb}{bd} เมื่อ b, d\neq 0
- เศษส่วนจำนวนคละ
- การบวก: a\frac{b}{c}+d\frac{e}{f}=\left(a+d\right)+\left(\frac{b}{c}+\frac{e}{f}\right) เมื่อ c, f\neq 0
- การลบ : a\frac{b}{c}-d\frac{e}{f}=\left(a-d\right)+\left(\frac{b}{c}-\frac{e}{f}\right) เมื่อ c, f\neq 0
การคูณและหารเศษส่วน
- การคูณ : \frac{a}{b}\times \frac{c}{d}=\frac{ac}{bd} เมื่อ b, d\neq 0
- การหาร : \frac{a}{b}\div \frac{c}{d}= \frac{a}{b}\times \frac{d}{c}=\frac{ad}{bc} เมื่อ b, c, d\neq 0
หมายเหตุ : จำนวนที่มีเครื่องหมายเหมือนกัน จะคูณหรือหารกัน ได้จำนวนบวก และเครื่องหมายต่างกันจะคูณหรือหารกัน ได้จำนวนลบ
รูปเรขาคณิตสองมิติและสามมิติ
หน้าตัดของรูปเรขาคณิตสามมิติ
หน้าตัดของรูปเรขาคณิตสามมิติเป็นรูปเรขาคณิตสองมิติแบบต่าง ๆ โดยจะขึ้นอยู่กับแนวการตัดของระนาบ
ตำแหน่งที่ตัด และชนิดของรูปเรขาคณิตสามมิติ เช่น
- ถ้าใช้ระนาบตัดในแนวขนานกับฐานของทรงสี่เหลี่ยมมุมฉาก จะได้หน้าตัดเป็นรูปสี่เหลี่ยมมุมฉาก
- ถ้าใช้ระนาบตัดในแนวที่ไม่ตั้งฉากและไม่ขนานกับฐานของทรงสี่เหลี่ยมมุมฉาก จะได้หน้าตัดเป็นรูปสี่เหลี่ยมมุมฉาก
- ถ้าใช้ระนาบตัดใกล้จุดยอดมุมของทรงสี่เหลี่ยมมุมฉาก จะได้หน้าตัดเป็นรูปสามเหลี่ยม
- ถ้าใช้ระนาบตัดพีระมิดฐานสามเหลี่ยมในแนวตั้งฉากกับฐาน จะได้หน้าตัดเป็นรูปสามเหลี่ยม
- ถ้าใช้ระนาบตัดทรงกระบอกในแนวขนานกับฐาน จะได้หน้าตัดเป็นวงกลม
- ถ้าใช้ระนาบตัดทรงกระบอกในแนวตั้งฉากกับฐาน จะได้หน้าตัดเป็นรูปสี่เหลี่ยมมุมฉาก
- ถ้าใช้ระนาบตัดกรวยในแนวตั้งฉากกับฐานผ่านจุดยอด จะได้หน้าตัดเป็นรูปสามเหลี่ยม
- ถ้าใช้ระนาบตัดกรวยในแนวเฉียงที่ไม่ขนานและไม่ตั้งฉากกับฐาน โดยไม่ผ่านฐานและจุดยอด จะได้หน้าตัดเป็นวงรี
- ถ้าใช้ระนาบตัดทรงกลมในแนวใด ๆ ก็ตาม จะได้หน้าตัดเป็นวงกลม



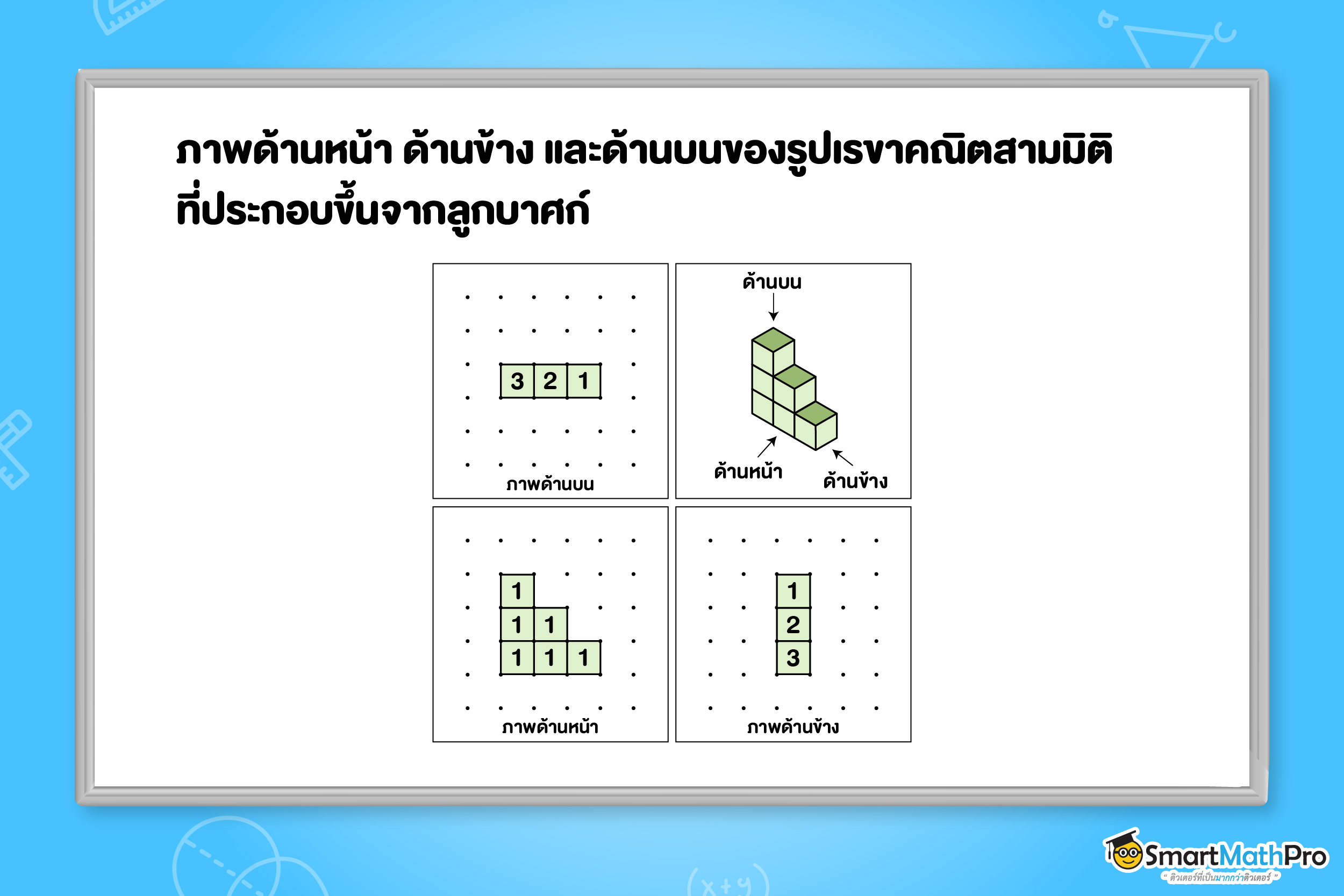
การเขียนภาพด้านหน้า ภาพด้านข้าง และภาพด้านบน
- รูปเรขาคณิตสามมิติ : เขียนจากการมองรูปเรขาคณิตสามมิติตามทิศทางที่แสดง โดยแนวสายตาตั้งฉากกับด้านที่มอง
- รูปเรขาคณิตสามมิติที่ประกอบขึ้นจากลูกบาศก์ : เขียนจากการมองรูปเรขาคณิตสามมิติตามทิศทางที่แสดง
พร้อมทั้งเขียนตัวเลขแสดงจำนวนลูกบาศก์ โดยผลรวมของจำนวนที่แสดงไว้ในภาพด้านหน้า ด้านข้าง และด้านบน
แต่ละภาพเท่ากัน และเท่ากับจำนวนลูกบาศก์ที่นำมาประกอบเป็นรูปนั้น ๆ ด้วย

สมการเชิงเส้นตัวแปรเดียว
วิธีแก้สมการเชิงเส้นตัวแปรเดียว
การแก้สมการจะใช้สมบัติของการเท่ากันในการหาคำตอบ เมื่อ a, b และ c แทนจำนวนจริงใด ๆ
- สมบัติสมมาตร : ถ้า a=b แล้ว b=a
- สมบัติถ่ายทอด : ถ้า a=b และ b=c แล้ว a=c
- สมบัติการเท่ากันเกี่ยวกับการบวก : ถ้า a=b แล้ว a+c=b+c
- สมบัติการเท่ากันเกี่ยวกับการคูณ : ถ้า a=b แล้ว ca=cb
อัตราส่วน สัดส่วน และร้อยละ
อัตราส่วน
อัตราส่วน a ต่อ b สามารถเขียนแทนด้วย a:b หรือ \frac{a}{b}
อัตราส่วนที่เท่ากัน
สามารถหาได้ 2 วิธี
- หลักการคูณ : นำจำนวนใด ๆ ที่ไม่เท่ากับศูนย์คูณทุกจำนวนของอัตราส่วนด้วยจำนวนเดียวกัน จะได้อัตราส่วนใหม่ที่เท่ากับอัตราส่วนเดิม
เช่น a:b=a\times c : b\times c โดย c\neq 0 - หลักการหาร : นำจำนวนใด ๆ ที่ไม่เท่ากับศูนย์หารทุกจำนวนของอัตราส่วนด้วยจำนวนเดียวกัน จะได้อัตราส่วนใหม่ที่เท่ากับอัตราส่วนเดิม
เช่น a:b=\frac {a}{c} : \frac{b}{c} โดย c\neq 0
การเปรียบเทียบการเท่ากันของอัตราส่วน
ทำได้ 3 วิธี
- การทำส่วนให้เท่ากัน
- การทำให้เป็นอัตราส่วนอย่างต่ำ
- การคูณไขว้
การหาอัตราส่วนต่อเนื่อง
จากอัตราส่วนของจำนวนสามจำนวน a:b:c เราสามารถเขียนอัตราส่วนของจำนวนทีละสองจำนวนได้เป็น a:b,
b:c และ a:c
สำหรับจำนวนบวก m ใด ๆ จะได้ว่า a:b=am:bm และ b:c=bm:cm ดังนั้น a:b:c=am:bm:cm
ในทำนองเดียวกัน ถ้ามีอัตราส่วนของจำนวนที่มากกว่าสามจำนวน ก็สามารถใช้หลักการเดียวกันนี้
เช่น a:b:c:d=am:bm:cm:dm เมื่อ m แทนจำนวนบวกใด ๆ
กราฟและความสัมพันธ์เชิงฟังก์ชัน
สมการเส้นตรง
y=mx+c เมื่อ m= ความชัน และ c= ระยะตัดแกน Y
สูตรคณิตศาสตร์ ม.2
ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง
รากที่สอง
รากที่สองของ a คือ จำนวนจริงที่ยกกําลังสองแล้วได้ a
รากที่สองของ a มีสองราก คือ
- รากที่สองที่เป็นบวก แทนด้วยสัญลักษณ์ \sqrt{a}
- รากที่สองที่เป็นลบ แทนด้วยสัญลักษณ์ -\sqrt{a}
สมบัติของรากที่สอง
กําหนดให้ a, b≥0
- ถ้า a<b แล้ว \sqrt{a}<\sqrt{b}
- \sqrt{a}\cdot\sqrt{b}=\sqrt{ab}
- \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}} โดยที่ b\neq 0
- \left(\sqrt{a}\right )^2=a
รากที่สาม
รากที่สามของ a คือ จำนวนจริงที่ยกกําลังสามแล้วได้ a เขียนแทนด้วยสัญลักษณ์ \sqrt[3]{a}
สมบัติของรากที่สาม
กําหนดให้ a,b เป็นจำนวนจริง
- ถ้า a<b แล้ว \sqrt[3]{a}<\sqrt[3]{b}
- \sqrt[3]{a}\cdot\sqrt[3]{b}= \sqrt[3]{ab}
- \frac{\sqrt[3]{a}}{\sqrt[3]{b}}=\sqrt[3]{\frac{a}{b}} โดยที่ b\neq 0
- \left(\sqrt[3]{a}\right )^3=a
ทฤษฎีบทพีทาโกรัส
สำหรับรูปสามเหลี่ยมมุมฉากใด ๆ ถ้า a และ b เป็นด้านประกอบมุมฉาก และ c เป็นด้านตรงข้ามมุมฉาก
แล้วจะได้ว่า c^2=a^2+b^2
ปริซึมและทรงกระบอก
ปริซึม
- สูตรหาพื้นที่ผิว = ( 2 \times พื้นที่ฐาน) + (ความยาวรอบฐาน \times ความสูง)
- สูตรหาปริมาตร = พื้นที่ฐาน \times ความสูง
ทรงกระบอก
- สูตรหาพื้นที่ผิว =2\pi r^2+2\pi rh
- สูตรหาปริมาตร =\pi r^2h
หมายเหตุ : เมื่อ r แทนรัศมีของฐานของทรงกระบอก และ h แทนความสูงของทรงกระบอก
การแปลงทางเรขาคณิต
การหาพิกัดของจุด ที่ได้จากการเลื่อนขนาน ไป x หน่วย
- A(a, b) เลื่อนขวา จะได้พิกัดใหม่เป็น A^{\prime}(a+x, b)
- A(a, b) เลื่อนซ้าย จะได้พิกัดใหม่เป็น A^{\prime}(a-x, b)
- A(a, b) เลื่อนขึ้นบน จะได้พิกัดใหม่เป็น A^{\prime}(a, b+x)
- A(a, b) เลื่อนลงล่าง จะได้พิกัดใหม่เป็น A^{\prime}(a, b-x)
การหาเวกเตอร์ของการเลื่อนขนาน
กำหนดให้ A^{\prime}(a^{\prime}, b^{\prime}) เป็นจุดที่ได้จากการเลื่อนขนาน A(a, b)
- a^{\prime}-a (ปลาย – ต้น)
- ได้จำนวนบวก : เลื่อนขวา \left|a^{\prime}-a \right| หน่วย
- ได้จำนวนลบ : เลื่อนซ้าย \left|a^{\prime}-a \right| หน่วย
- b^{\prime}-b (ปลาย – ต้น)
- ได้จำนวนบวก : เลื่อนขึ้น \left|b^{\prime}-b \right| หน่วย
- ได้จำนวนลบ : เลื่อนลง \left|b^{\prime}-b \right| หน่วย
การหาพิกัดของจุดที่ได้จากการสะท้อน โดยมีเส้นตรงต่อไปนี้เป็นเส้นสะท้อน
- A(a, b) สะท้อนข้ามแกน X จะได้พิกัดใหม่เป็น A^{\prime}(a, -b)
- A(a, b) สะท้อนข้ามแกน Y จะได้พิกัดใหม่เป็น A^{\prime}(-a, b)
- A(a, b) สะท้อนข้ามเส้นตรง y=x จะได้พิกัดใหม่เป็น A^{\prime}(b,a)
- A(a, b) สะท้อนข้ามเส้นตรง y=-x จะได้พิกัดใหม่เป็น A^{\prime}(-b, -a)
การหาสมการของเส้นตรงที่เป็นเส้นสะท้อน
กำหนดให้ A^{\prime}(a^{\prime}, b^{\prime}) เป็นจุดที่ได้จากการสะท้อน A(a, b)
- ถ้า a=a^{\prime} (y เปลี่ยนแปลง) แล้ว เส้นสะท้อนคือ y=\frac{b+b^{\prime}}{2}
- ถ้า b=b^{\prime} (x เปลี่ยนแปลง) แล้ว เส้นสะท้อนคือ x=\frac{a+a^{\prime}}{2}
- ถ้าพิกัดตัวหน้าและตัวหลังของ A และ A^{\prime} สลับกันแล้ว เส้นสะท้อนคือ y=x
- ถ้าพิกัดตัวหน้าและตัวหลังของ A, A^{\prime} สลับกัน และเป็นจำนวนตรงข้ามแล้ว เส้นสะท้อนคือ y=-x
การหาพิกัดของจุดที่ได้จากการหมุน โดยมีจุดกำเนิดเป็นจุดหมุน
- A(a, b) หมุนตามเข็ม 90^{\circ} จะได้พิกัดใหม่เป็น A^{\prime}(b,-a)
- A(a, b) หมุนทวนเข็ม 90^{\circ} จะได้พิกัดใหม่เป็น A^{\prime}(-b,a)
- A(a, b) หมุนตามเข็ม 180^{\circ} จะได้พิกัดใหม่เป็น A^{\prime}(-a,-b)
- A(a, b) หมุนทวนเข็ม 180^{\circ} จะได้พิกัดใหม่เป็น A^{\prime}(-a,-b)
สมบัติของเลขยกกำลัง
สมบัติของเลขยกกำลัง
เมื่อ a,b เป็นจำนวนจริงใด ๆ ที่ไม่เท่ากับ 0 และ m,n เป็นจำนวนเต็ม
- a^{m}\times a^{n} =a^{m+n}
- a^{m} \div a^{n} =a^{m-n}
- \left( a^{m} \right)^{n}=a^{mn}
- \left( ab\right)^{n}=a^{n}b^{n}
- \left( \frac{a}{b} \right)^{n}=\frac{a^{n}}{b^{n}}
พหุนาม
เอกนาม
- ผลบวกหรือผลลบของเอกนาม = (ผลบวกหรือผลลบของสัมประสิทธิ์) \times (ส่วนที่อยู่ในรูปของตัวแปรหรือการคูณกันของตัวแปร)
- ผลคูณหรือผลหารของเอกนามกับเอกนาม = (ผลคูณหรือผลหารของสัมประสิทธิ์) \times (ตัวแปรคูณหรือหารกันโดยใช้สมบัติของเลขยกกำลัง)
พหุนาม
- ผลบวกหรือผลลบของพหุนาม หาจากการบวกหรือลบพจน์ที่คล้ายกันเข้าด้วยกัน
- การคูณพหุนามกับพหุนาม หาจากการคูณกระจายเข้าไปในทุก ๆ พจน์
- การหารพหุนามด้วยเอกนาม หาจากการหารแต่ละพจน์ของพหุนามด้วยเอกนามที่เป็นตัวหาร
การแยกตัวประกอบพหุนามดีกรีสอง
กำหนดให้ A แทนพจน์หน้า และ B แทนพจน์หลัง
- กำลังสองสมบูรณ์
- A^2+2AB+B^2= \left(A+B\right )^2
- A^2-2AB+B^2= \left(A-B\right )^2
- ผลต่างของกำลังสอง
- A^2-B^2= \left(A-B\right )\left(A+B\right )
สถิติ(2)
- ค่าเฉลี่ยเลขคณิต = \frac{ผลบวกของข้อมูลทั้งหมด}{จำนวนข้อมูล}
- มัธยฐาน หาจากการนำข้อมูลเรียงจากน้อยไปมาก หรือเรียงจากมากไปน้อย และพิจารณาข้อมูลที่อยู่ตรงกลางหรือค่าเฉลี่ยของข้อมูลคู่ที่อยู่ตรงกลาง
- ฐานนิยม ดูจากข้อมูลที่มีความถี่สูงสุดในข้อมูลชุดนั้น
สูตรคณิตศาสตร์ ม.3
อสมการเชิงเส้นตัวแปรเดียว
การแก้อสมการเชิงเส้นตัวแปรเดียวใช้สมบัติของการไม่เท่ากัน (properties of inequality) ในการหาคำตอบ
สมบัติการบวกของการไม่เท่ากัน
ให้ a,b และ c แทนจำนวนจริงใด ๆ
- ถ้า a<b แล้ว a+c<b+c
- ถ้า a>b แล้ว a+c>b+c
- ถ้า a≤b แล้ว a+c≤b+c
- ถ้า a≥b แล้ว a+c≥b+c
สมบัติการคูณของการไม่เท่ากัน
ให้ a และ b แทนจำนวนจริงใด ๆ และ c แทนจำนวนจริงบวก
- ถ้า a<b แล้ว ac<bc
- ถ้า a ≤ b แล้ว ac ≤ bc
- ถ้า a>b แล้ว ac>bc
- ถ้า a≥b แล้ว ac≥bc
ให้ a และ b แทนจำนวนจริงใด ๆ และ c แทนจำนวนจริงลบ
- ถ้า a<b แล้ว ac>bc
- ถ้า a ≤ b แล้ว ac≥bc
- ถ้า a>b แล้ว ac<bc
- ถ้า a≥b แล้ว ac ≤ bc
การแยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง
การแยกตัวประกอบพหุนามดีกรีสาม
กำหนดให้ A แทนพจน์หน้า และ B แทนพจน์หลัง
- ผลบวกของกำลังสาม : A^3+B^3=\left(A+B\right)\left(A^2-AB+B^2\right )
- ผลต่างของกำลังสาม : A^3-B^3=\left(A-B\right)\left(A^2+AB+B^2\right )
- กำลังสามสมบูรณ์ :
- A^3+3A^2B+3AB^2+B^3=\left(A+B\right)^3
- A^3-3A^2B+3AB^2-B^3=\left(A-B\right)^3
การแยกตัวประกอบพหุนามดีกรีสูงกว่าสาม
ให้จัดรูปพหุนามให้อยู่ในรูปดังต่อไปนี้ ก่อนแยกตัวประกอบ
- ผลต่างของกำลังสอง
- กำลังสองสมบูรณ์
- ผลบวกของกำลังสาม
- ผลต่างของกำลังสาม
- ใช้แนวคิดจากการแยกตัวประกอบของพหุนามดีกรีสอง
สมการกำลังสองตัวแปรเดียว
รูปทั่วไปของสมการกำลังสองตัวแปรเดียว
ax^2+bx+c=0 เมื่อ a,b และ c เป็นค่าคงตัว โดยที่ a\neq 0
วิธีแก้สมการกำลังสองตัวแปรเดียว
วิธีที่ 1 แทนค่าตัวแปร
วิธีที่ 2 ถ้าแยกสองวงเล็บได้ง่าย
แยกตัวประกอบพหุนามดีกรีสอง โดยการแยกเป็น 2 วงเล็บ
วิธีที่ 3 ถ้าแยกสองวงเล็บได้ยาก
- จัดรูปโดยใช้สูตรกำลังสองสมบูรณ์
- ใช้สูตร x=\frac{-b \pm \sqrt{b^2 – 4ac} }{2a} โดยคำตอบจะมี 3 ลักษณะ ได้แก่
- ถ้า b^2-4ac>0 จะมี 2 คำตอบ
- ถ้า b^2-4ac=0 จะมี 1 คำตอบ
- ถ้า b^2-4ac<0 สมการจะไม่มีคำตอบที่เป็นจำนวนจริง
ผลบวกและผลคูณของคำตอบของสมการ
ax^2+bx+c=0 เมื่อ a,b และ c เป็นค่าคงตัว โดยที่ a\neq 0 และ b^2-4ac>0
- ผลบวกของคำตอบ คือ -\frac{b}{a}
- ผลคูณของคำตอบ คือ \frac{c}{a}
พาราโบลา (ฟังก์ชันกำลังสอง)
สมการของพาราโบรา (สมการฟังก์ชันกำลังสอง)
y=ax^2+bx+c เมื่อ a,b และ c เป็นค่าคงตัว โดยที่ a\neq 0
กราฟของพาราโบลา (สมการฟังก์ชันกำลังสอง)
จัดสมการ y=ax^2+bx+c ให้อยู่ในรูป y=a\left ( x-h \right )^2+k
โดยจุดยอดของพาราโบลาสามารถหาได้จากสูตร (h, k) = \left (-\frac{b}{2a},\frac{4ac-b^2}{4a}\right)
สถิติ (3)
การหาควอร์ไทล์
วิธีการหาควอร์ไทล์ (Q) ในตำแหน่งต่าง ๆ มีขั้นตอนดังนี้
- เรียงข้อมูลจากน้อยไปหามาก
- หามัธยฐานของข้อมูลทั้งหมด ซึ่งค่าที่ได้นั้นจะเป็น Q_{2}
- หามัธยฐานของข้อมูลเฉพาะข้อมูลที่มีลำดับต่ำกว่า Q_{2} จะได้ค่าดังกล่าวคือ Q_{1}
- หามัธยฐานของข้อมูลเฉพาะข้อมูลที่มีลำดับสูงกว่า Q_{2} จะได้ค่าดังกล่าวคือ Q_{3}
การสร้างแผนภาพกล่อง
- เรียงข้อมูลจากน้อยไปหามาก
หาค่าต่ำสุดของข้อมูล, ค่าสูงสุดของข้อมูล, Q_{1}, Q_{2}, Q_{3} - เขียนสเกลและนำค่าที่ได้มาลงจุด
- สร้างกล่อง
- สร้างวิสเกอร์

พื้นที่ผิวและปริมาตร (พีระมิด กรวย และทรงกลม)
พีระมิด
- สูตรหาพื้นที่ผิว
- พื้นที่ฐาน + พื้นที่ผิวข้าง
- พื้นที่ฐาน + (\frac{1}{2}\times ความยาวรอบรูปของฐาน \times ส่วนสูงเอียง)
- สูตรหาปริมาตร =\frac{1}{3}\times พื้นที่ฐาน \times ความสูง
กรวย
- สูตรหาพื้นที่ผิว = พื้นที่ฐาน +พื้นที่ผิวข้าง หรือ \pi r^2+\pi rl
- สูตรหาปริมาตร =\frac{1}{3}\pi r^2h
หมายเหตุ : เมื่อ r แทนรัศมีของฐานกรวย, l แทนส่วนสูงเอียงของกรวย และ h แทนความสูงของกรวย
ทรงกลม
- สูตรหาพื้นที่ผิว =4\pi r^2
- สูตรหาปริมาตร =\frac{4}{3}\pi r^3
หมายเหตุ : เมื่อ r แทนรัศมีของทรงกลม
ความน่าจะเป็น
ความน่าจะเป็นของเหตุการณ์ P(E)=\frac{จำนวนผลลัพธ์ของเหตุการณ์ n(E)}{จำนวนผลลัพธ์ทั้งหมดที่เกิดขึ้นจากการทดลองสุ่ม n(S)}
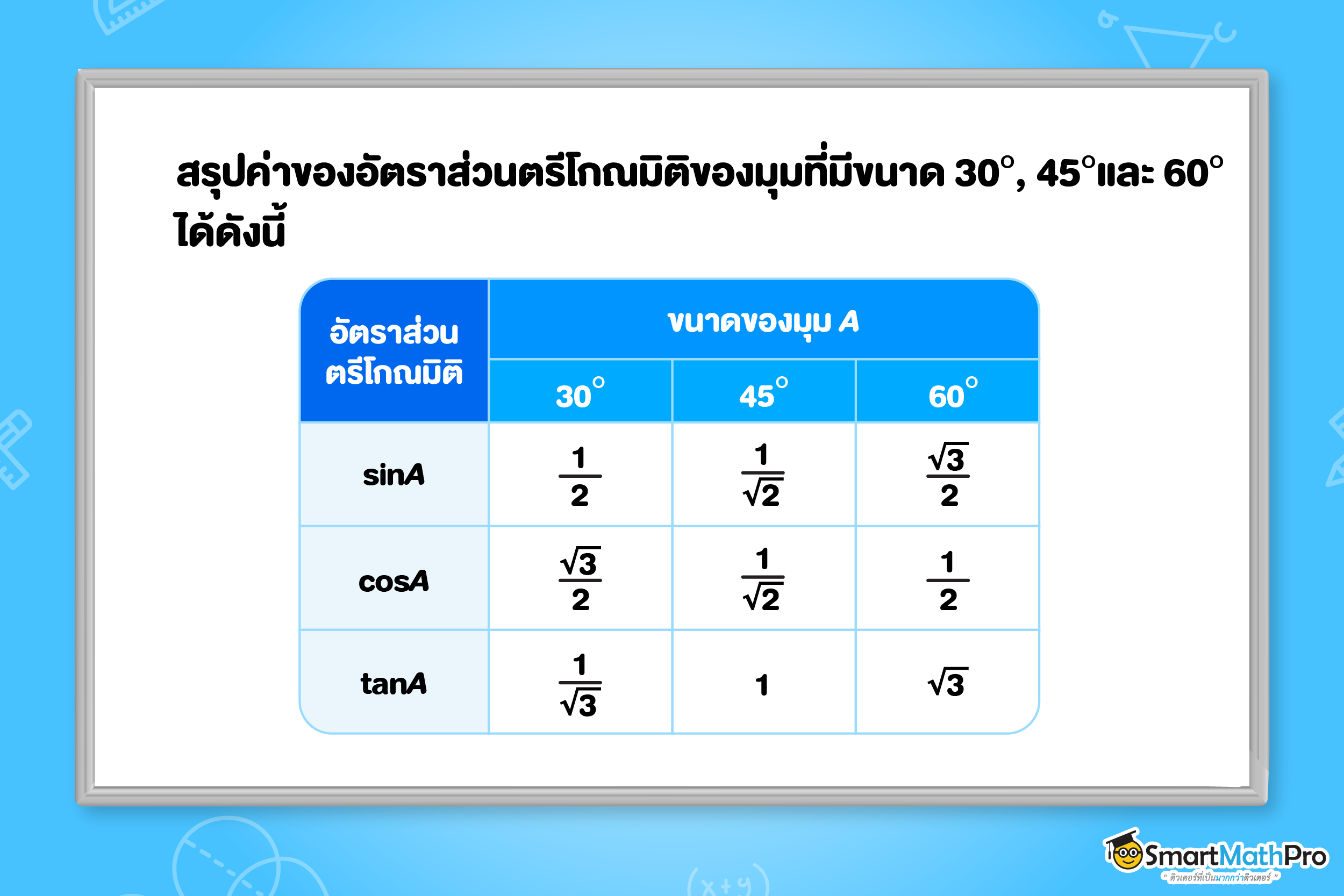
อัตราส่วนตรีโกณมิติ
อัตราส่วนตรีโกณมิติของมุม A
- \text{sin}A = \frac{ข้าม}{ฉาก}
- \text{cos}A = \frac{ชิด}{ฉาก}
- \text{tan}A = \frac{ข้าม}{ชิด}
ค่าอัตราส่วนตรีโกณมิติของมุม 30^{\circ}, 45^{\circ}, 60^{\circ}
ติวคณิตศาสตร์กับ SmartMathPro
น้อง ๆ คนไหนที่ยังไม่แม่นในเนื้อหา อยากได้คนช่วยแนะนำแนวทางนการเตรียมสอบ หรืออยากได้คนช่วยไกด์แนวทางให้
สำหรับน้อง ๆ ม.3 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์
พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.3 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก
เป็นอย่างไรกันบ้างกับสูตรคณิต ม.ต้น ที่ควรรู้ที่พี่เอามาฝาก จะเห็นว่ามีสูตรค่อนข้างเยอะเลยน้าา แต่พี่เชื่อว่าถ้าน้อง ๆ จำสูตรเหล่านี้ได้ ก็จะช่วยให้แก้โจทย์และทำข้อสอบได้เร็วขึ้นด้วย และสำหรับน้อง ๆ คนไหนที่อยากได้โจทย์หรือแบบฝึกหัดคณิตศาสตร์ ม.ต้น ก็สามารถเข้าไปดูที่ คลังข้อสอบคณิตศาสตร์ ม.ต้น ได้น้าา บอกเลยว่ามีโจทย์ให้ฝึกมือเพียบบ
บทความ แนะนำ
บทความ แนะนำ

พี่ออม ทีมบทความ SmartMathPro
ป.ตรี คณะมนุษยศาสตร์ สาขาวิชาภาษาอังกฤษ มศว
พี่สาวที่หลงใหลในเสียงเพลงและรักในการเขียนบทความ ไม่ว่าจะเป็นบทความแนะแนว TCAS หรือบทความแนะแนวการศึกษา พี่ก็พร้อมทำเพื่อน้อง ๆ ที่ฝันอยากเข้ามหาลัยฯ ทุกคน !

พี่ออม ทีมบทความ SmartMathPro
ป.ตรี คณะมนุษยศาสตร์ สาขาวิชาภาษาอังกฤษ มศว
พี่สาวที่หลงใหลในเสียงเพลงและรักในการเขียนบทความ ไม่ว่าจะเป็นบทความแนะแนว TCAS
หรือบทความแนะแนวการศึกษา พี่ก็พร้อมทำเพื่อ
น้อง ๆ ที่ฝันอยากเข้ามหาลัยฯ ทุกคน !
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
















