สมบัติของเลขยกกำลัง ม.2 สรุปเนื้อหาพร้อมโจทย์และเฉลย

หลายคนน่าจะเคยได้ยินคำว่า “เลขยกกำลัง” เพราะเป็นเนื้อหาที่เจอในหลาย ๆ บทและได้เรียนกันมาตั้งแต่ ม.1 แต่สำหรับบทเรียนในคณิตศาสตร์ ม.2 นั้น น้อง ๆ จะได้เรียนเกี่ยวกับ “สมบัติของเลขยกกำลัง” ที่จะช่วยให้คิดคำนวณได้รวดเร็วและเป็นระบบมากขึ้น

ซึ่งถ้าใครอยากจะอ่านสรุปหรือทบทวนเนื้อหา ก็สามารถอ่านได้ที่บทความนี้เลยเพราะว่าพี่เตรียมสรุปเนื้อหา
“สมบัติของเลขยกกำลัง” มาให้แล้ว และเพื่อเสริมความเข้าใจให้มากขึ้น ก็ยังมีตัวอย่างโจทย์และแบบฝึกหัดพร้อมเฉลยให้ลองทำท้ายบทความอีกด้วยย

สนใจหัวข้อไหน ... กดอ่านเลย

ภาพรวมสมบัติของเลขยกกำลัง ม.2

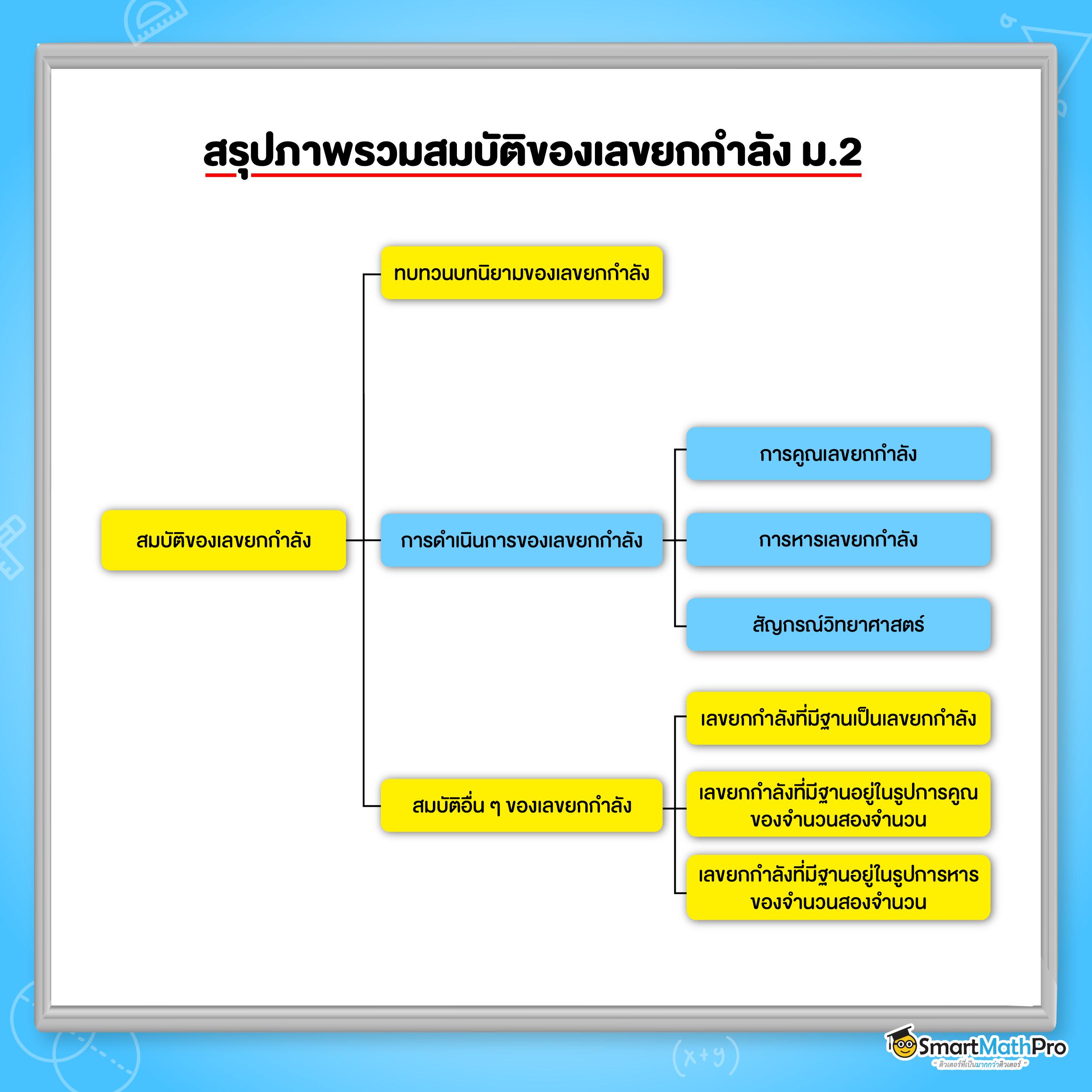
เลขยกกำลัง คืออะไร ?

อย่างที่พี่กล่าวไปข้างต้นว่า น้อง ๆ คงเคยเรียนและรู้จักกับเลขยกกำลังมาแล้วในระดับชั้น ม.1 ว่าการยกกำลังคือ
การคูณซ้ำ ๆ เช่น $3^{3}= 3 \times 3\times 3$
แต่ในระดับ ม.2 นี้ เราจะเรียนเรื่อง “สมบัติของเลขยกกำลัง” กัน แต่ก่อนที่จะไปสู่สมบัติของเลขยกกำลังเรามาทบทวน
บทนิยามหรือความหมายของเลขยกกำลังกันหน่อยดีกว่า

บทนิยาม
ให้ $a$ เป็นจำนวนจริงและ $n$ เป็นจำนวนเต็มบวก $a^{n}=a \times a\times a\times \cdots \times a$ จำนวน $n$ ตัว และถ้า $a\neq 0$ จะกำหนดให้ $a^{0}=1$ และ $a^{-n}=\frac{1}{a^{n}}$

การดำเนินการของเลขยกกำลัง

เมื่อน้อง ๆ ได้ทบทวนความหมายของเลขยกกำลังเป็นที่เรียบร้อยแล้ว ขั้นต่อไปเราจะนำเลขยกกำลังมาดำเนินการกัน ซึ่งจะประกอบไปด้วย การคูณและการหารเลขยกกำลัง

การคูณเลขยกกำลัง

สมบัติ

ให้ $a$ เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ $0$ และ $m, n$ เป็นจำนวนเต็ม

$a^{m}\cdot a^{n}=a^{m+n}$

ตัวอย่าง

$3^{4}\cdot 3^{2}=3^{4+2}=3^{6}$

ตัวอย่างที่ 1 จงหาผลคูณ $2^{-4}\times 64$ ในรูปเลขยกกำลัง

วิธีทำ $2^{-4}\times 64 =2^{-4}\times 2^{6} \\ =2^{-4+6} \\ =2^{2}$

ตัวอย่างที่ 2 จงหาผลคูณ $a^{-3}\times a^{5}\times a^{2}$ ในรูปเลขยกกำลัง เมื่อ $a\neq 0$

วิธีทำ $a^{-3}\times a^{5}\times a^{2}=a^{-3+5+2} \\ =a^{4}$

การหารเลขยกกำลัง

สมบัติ

ให้ $a$ เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ $0$ และ $m, n$ เป็นจำนวนเต็ม

$\frac{a^{m}}{a^{n}}=a^{m-n}$

ตัวอย่าง

$\frac{5^{6}}{5^{3}}=5^{6-3}=5^{3}$

ตัวอย่างที่ 3 จงหาผลคูณ $\frac{6^{6}\times 36}{216}$ ในรูปเลขยกกำลัง

วิธีทำ $\frac{6^{6}\times 36}{216}=\frac{6^{6}\times 6^{2}}{6^{3}} \\ =6^{6+2-3} \\ =6^{5}$

ตัวอย่างที่ 4 จงหาผลคูณ $\frac{x^{3}\times x^{-2}}{x^{-6}}$ ในรูปเลขยกกำลัง เมื่อ $x\neq 0$

วิธีทำ $\frac{x^{3}\times x^{-2}}{x^{-6}}=x^{3+(-2)-(-6)} \\ =x^{7}$

สัญกรณ์วิทยาศาสตร์

สัญกรณ์วิทยาศาสตร์ (Scientific notation) คือ รูปแบบของการเขียนจำนวนอย่างหนึ่ง เพื่อให้สามารถเขียนจำนวนที่มีขนาดใหญ่มากหรือเล็กมาก ให้ง่ายขึ้นและสะดวกขึ้น โดยเขียนในรูปการคูณของเลขยกกำลังที่มีฐานเป็นสิบและมีเลขชี้กำลังเป็นจำนวนเต็ม มีรูปทั่วไป คือ

$A\times 10^{n}$ เมื่อ $1\le A\lt 10$ และ $n$ เป็นจำนวนเต็ม

ตัวอย่างที่ 5 จงหาผลลัพธ์ของ $(7\times 10^{4}) \cdot(2\times 10^{3})$ ในรูปสัญกรณ์วิทยาศาสตร์
วิธีทำ $(7\times 10^{4}) \cdot(2\times 10^{3})= (7\times 2) \cdot(10^{4}\times 10^{3}) \\ =14\times 10^{7} \\ =(1.4\times 10)\times 10^{7} \\ =1.4\times 10^{8}$

สมบัติอื่น ๆ ของเลขยกกำลัง

เมื่อน้อง ๆ เข้าใจพื้นฐานการดำเนินการของเลขยกกำลังดีแล้ว เราลองมาเรียนรู้สมบัติอื่น ๆ เพิ่มเติมกันดีกว่า

เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง

สมบัติ

ให้ $a$ เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ $0$ และ $m, n$ เป็นจำนวนเต็ม

$\left( a^{m} \right )^{n}=a^{m\cdot n}$

ตัวอย่าง

$\left( 5^{3} \right )^{2}=5^{3\cdot 2} \\=5^6$

ตัวอย่างที่ 6 จงหาผลลัพธ์ของ $27^{-2}$ ในรูปเลขยกกำลังที่มีฐานเป็นจำนวนเฉพาะและมีเลขชี้กำลังเป็นจำนวนเต็มบวก

วิธีทำ $27^{-2}=\left( 3^{3} \right)^{-2} \\ =3^{3\cdot (-2)} \\ =3^{-6} \\ =\frac{1}{3^{6}}$

ตัวอย่างที่ 7 จงหาผลลัพธ์ของ $8^{2}\times 2^{-4}$ ในรูปเลขยกกำลังที่มีฐานเป็นจำนวนเฉพาะและมีเลขชี้กำลังเป็นจำนวนเต็มบวก

วิธีทำ $8^{2}\times 2^{-4}=\left( 2^{3} \right)^{2}\times 2^{-4} \\ =2^{3\cdot 2}\times 2^{-4} \\ =2^{6+(-4)} \\ =2^{2}$

เลขยกกำลังที่มีฐานอยู่ในรูปการคูณของจำนวนสองจำนวน

สมบัติ

ให้ $a$ เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ $0$ และ $m, n$ เป็นจำนวนเต็ม

$\left (ab\right)^{n}=a^{n}\cdot b^{n}$

ตัวอย่าง

$(3\cdot 7)^{4}=3^{4}\cdot 7^{4}$

ตัวอย่างที่ 8 จงหาผลลัพธ์ของ $36^{3}$ ในรูปเลขยกกำลังที่มีฐานเป็นจำนวนเฉพาะและมีเลขชี้กำลังเป็นจำนวนเต็มบวก

วิธีทำ $36^{3} =\left( 6^{2} \right)^{3} \\ =6^{2\cdot 3} \\ =(2\cdot3)^{6} \\ =2^{6} \cdot3^{6}$

ตัวอย่างที่ 9 กำหนดให้ $a,b$ เป็นจำนวนเฉพาะ จงหาผลลัพธ์ของ $\left( 9ab^{-4} \right)^{-2}$ ในรูปเลขยกกำลังที่มีฐานเป็นจำนวนเฉพาะและมีเลขชี้กำลังเป็นจำนวนเต็มบวก

วิธีทำ $\left( 9ab^{-4} \right)^{-2} =\left( 3^{2}ab^{-4} \right)^{-2} \\ =3^{2\cdot (-2)}a^{1\cdot(-2)}b^{-4\cdot (-2)} \\ =3^{-4}a^{-2}b^{8} \\ =\frac{b^{8}}{3^{4}a^{2}}$

เลขยกกำลังที่มีฐานอยู่ในรูปการหารของจำนวนสองจำนวน

สมบัติ

ให้ $a, b$ เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ $0$ และ $n$ เป็นจำนวนเต็ม

$\left ( \frac{a}{b} \right )^{n}=\frac{a^{n}}{b^{n}}$

ตัวอย่าง

$\left ( \frac{3}{5} \right )^{4}=\frac{3^{4}}{5^{4}}$

ตัวอย่างที่ 10 จงหาผลลัพธ์ของ $\left ( \frac{1}{7^{3}} \right )^{-4}$ ในรูปเลขยกกำลังที่มีฐานเป็นจำนวนเฉพาะและมีเลขชี้กำลังเป็นจำนวนเต็มบวก

วิธีทำ $\left ( \frac{1}{7^{3}} \right )^{-4}=\frac{1^{-4}}{7^{3\cdot (-4)}} \\ =\frac{1}{7^{-12}} \\ =7^{12}$

ตัวอย่างที่ 11 จงหาผลลัพธ์ของ $\frac{16}{\left( \frac{2}{25^{-1}} \right)^3}$ ในรูปเลขยกกำลังที่มีฐานเป็นจำนวนเฉพาะและมีเลขชี้กำลังเป็นจำนวนเต็มบวก

วิธีทำ $\frac{16}{\left(\frac{2}{25^{-1}}\right )^{3}}=\frac{2^{4}}{\frac{ 2^{1\cdot 3}}{(5^{2})^{(-1)\cdot 3 }}} \\ =\frac{2^{4}}{\frac{2^{3}}{5^{-6}}} \\ =2^{4} \div \frac{2^{3}}{{5^{-6}}} \\ =2^{4} \times \frac{5^{-6}}{{2^{3}}} \\ =2^{4-3}\cdot 5^{-6} \\ =\frac{2}{5^{6}}$

สรุปบทนิยามและสมบัติของเลขยกกำลัง ม.2

ติวคณิตศาสตร์ ม.ต้น กับ SmartMathPro

สำหรับน้อง ๆ ม.2 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์

พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.2 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน แนวข้อสอบเข้าม.4 และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก เลย

สำหรับใครที่อยากแม่นเนื้อหาสมบัติเลขยกกำลัง ม.2 พี่แนะนำว่าควรทบทวนเนื้อหาอย่างสม่ำเสมอและลองฝึกทำ
แบบฝึกหัดเพิ่มเติมด้วยน้า