สรุปความเท่ากันทุกประการ ม.2 พร้อมโจทย์และเฉลยฟรี

ใครกำลังรอสรุปเนื้อหาเรื่อง ความเท่ากันทุกประการ ม.2 สามารถดูได้จากบทความนี้เลยน้า โดยในบทความนี้
พี่จะพาน้อง ๆ ไปรู้จักความเท่ากันทุกประการให้มากยิ่งขึ้น ทั้งเรื่องความหมาย, ความเท่ากันทุกประการของรูปเรขาคณิต, ความเท่ากันทุกประการของรูปสามเหลี่ยม, การนำความเท่ากันทุกประการไปใช้ พร้อมแจกแบบฝึกหัด+เฉลยให้น้อง ๆ ได้ลองทำกันท้ายบทความด้วยน้าา

สนใจหัวข้อไหน ... กดอ่านเลย

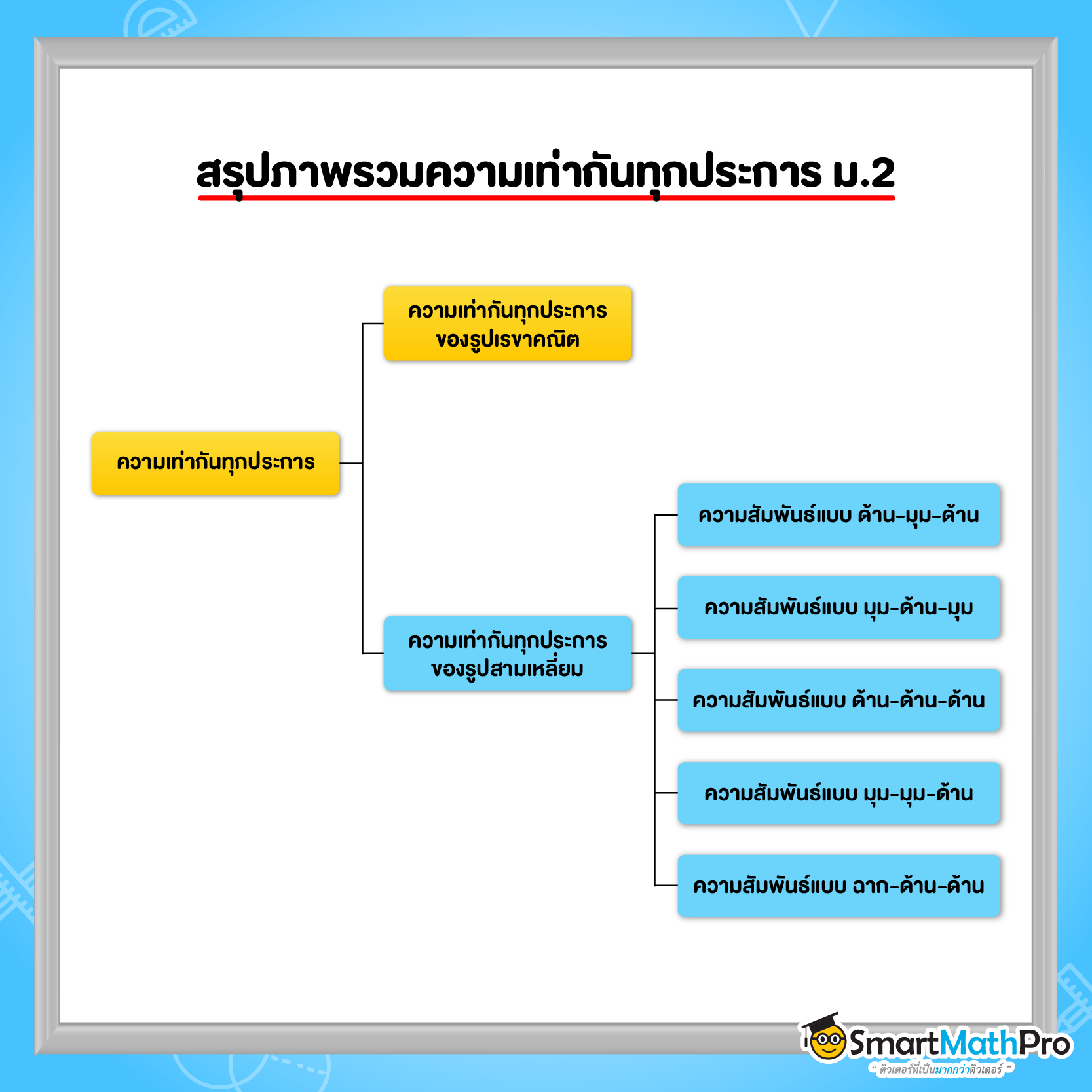
ความเท่ากันทุกประการ ม.2

ความเท่ากันทุกประการคืออะไร ?

ในชีวิตประจำวันของเรา น้องจะเห็นสิ่งของหลาย ๆ อย่างที่มีรูปร่างเหมือนกัน เช่น ภาชนะใส่อาหาร หรืออาคารบางอาคารที่มีการออกแบบให้มีขนาดหรือรูปร่างที่เหมือนกัน

โครงสร้างที่ประกอบจากรูปสามเหลี่ยมที่เท่ากันของสิ่งก่อสร้างในสถานที่ต่าง ๆ ออกแบบเพื่อให้เกิดความแข็งแรง ซึ่งสิ่งของเหล่านั้นมักประกอบด้วยรูปเรขาคณิตในการออกแบบด้วย

ความเท่ากันทุกประการของรูปเรขาคณิต

ในทางคณิตศาสตร์ เมื่อสามารถเคลื่อนที่รูปเรขาคณิตรูปหนึ่งไปทับอีกรูปหนึ่งได้สนิท โดยใช้การแปลงทางเรขาคณิต
จะกล่าวว่ารูปเรขาคณิตสองรูปนั้นเท่ากันทุกประการ ซึ่งเป็นไปตามบทนิยามของความเท่ากันทุกประการ (congruence) ของรูปเรขาคณิตบนระนาบดังนี้

บทนิยาม
รูปเรขาคณิตสองรูปเท่ากันทุกประการ ก็ต่อเมื่อ เคลื่อนที่รูปหนึ่งไปทับอีกรูปหนึ่งได้สนิท

จากบทนิยาม เราสามารถกล่าวว่า “ถ้ารูปเรขาคณิตสองรูปเท่ากันทุกประการ แล้วจะเคลื่อนที่รูปหนึ่งไปทับอีกรูปหนึ่งได้สนิท” และ “ถ้าเคลื่อนที่รูปหนึ่งไปทับอีกรูปหนึ่งได้สนิท แล้วรูปเรขาคณิตสองรูปนั้นเท่ากันทุกประการ” ได้เช่นกัน
เมื่อรูปเรขาคณิต A และรูปเรขาคณิต B เท่ากันทุกประการ จะเขียนแทนด้วยสัญลักษณ์ว่า รูป A $\cong$ รูป B อ่านว่า “รูป A เท่ากันทุกประการกับรูป B” หรือ “รูป A และรูป B เท่ากันทุกประการ”ก็ได้เหมือนกันน้า

ตัวอย่างที่ 1

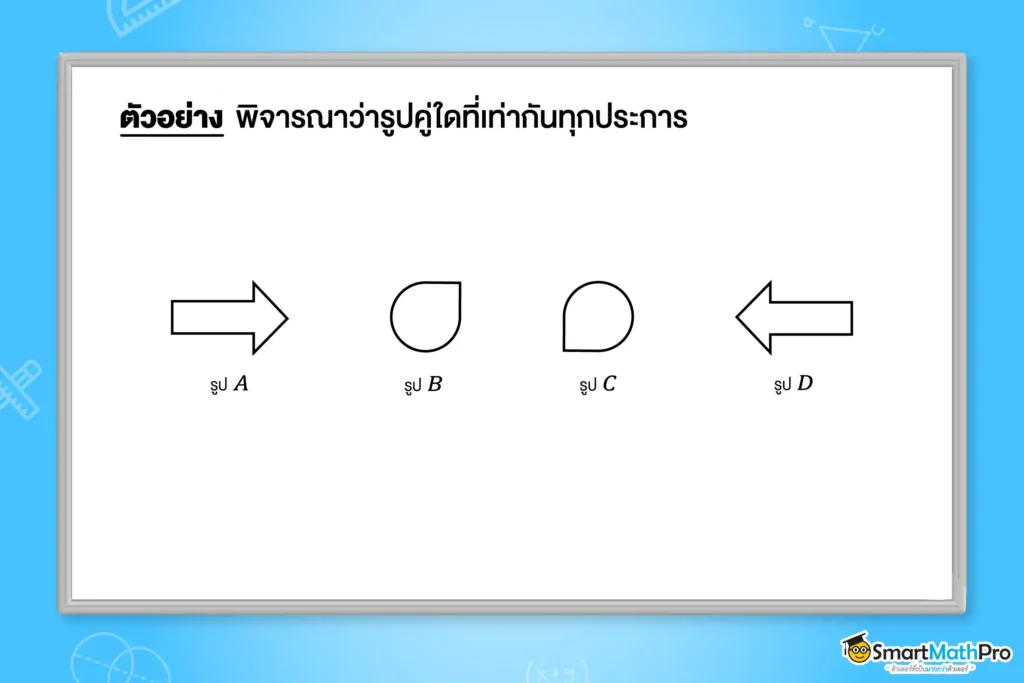
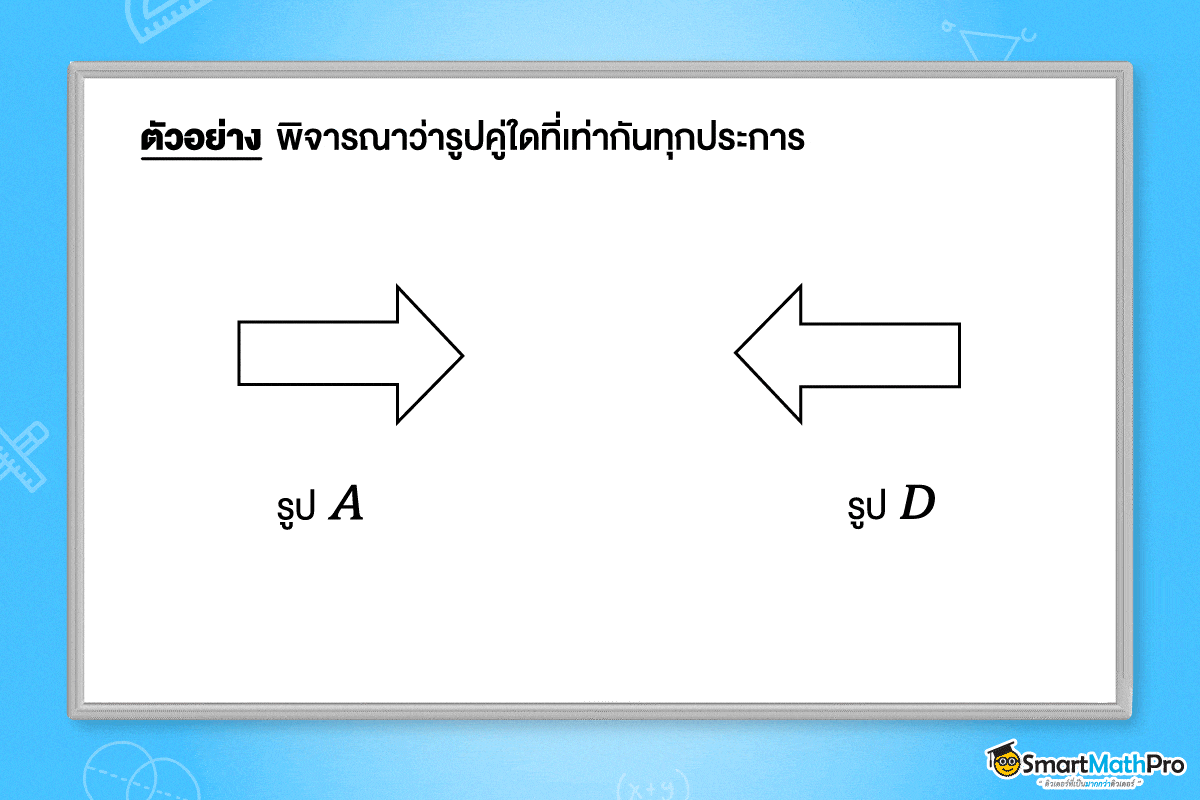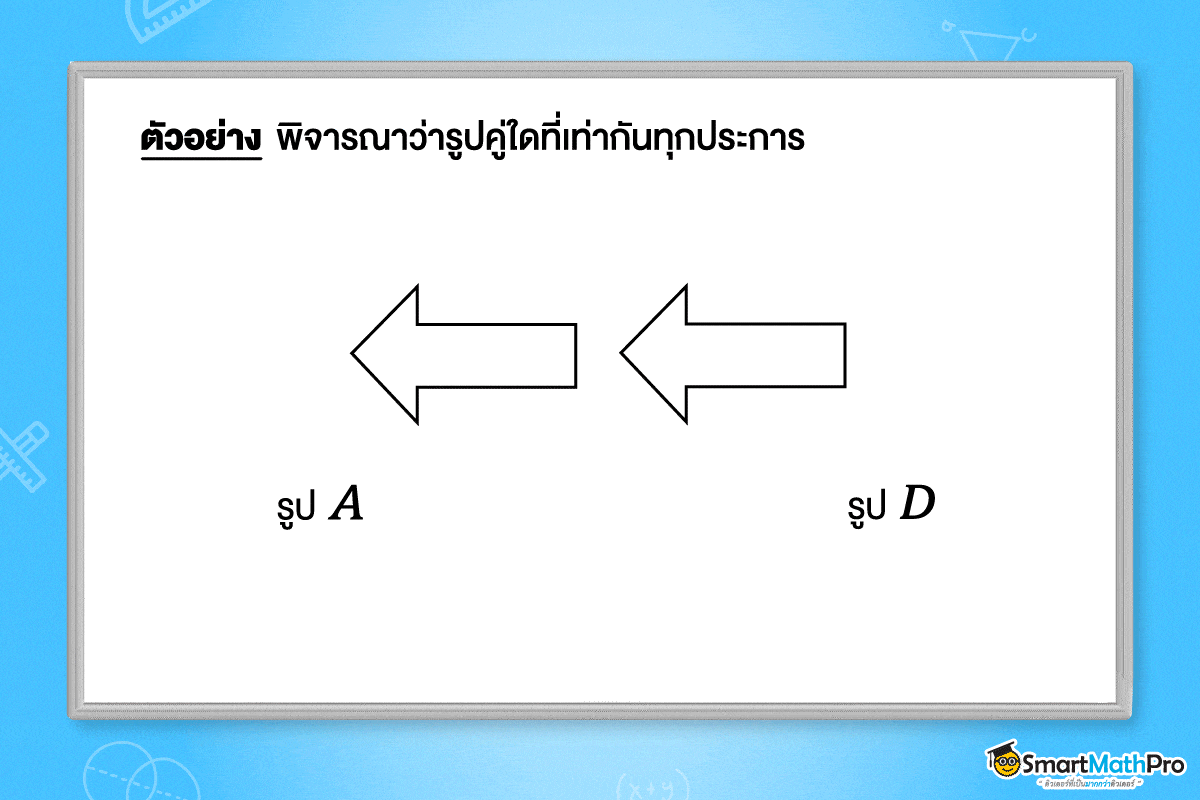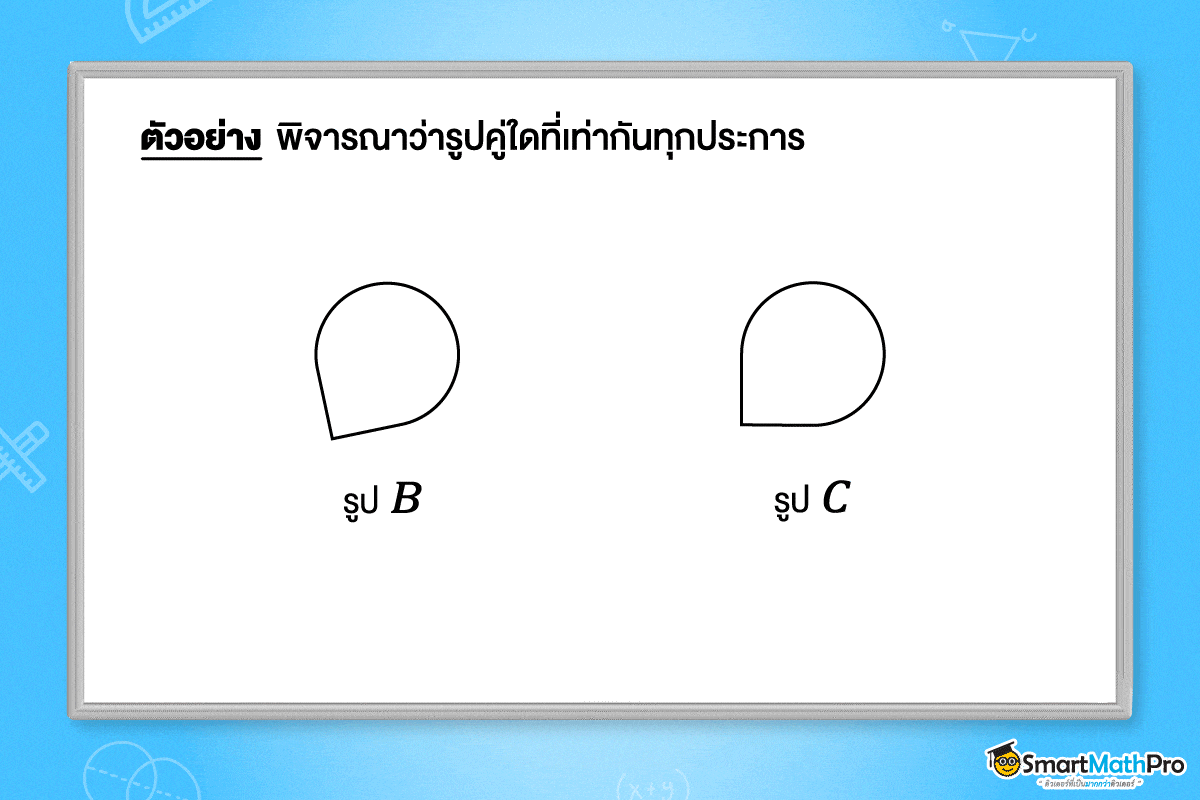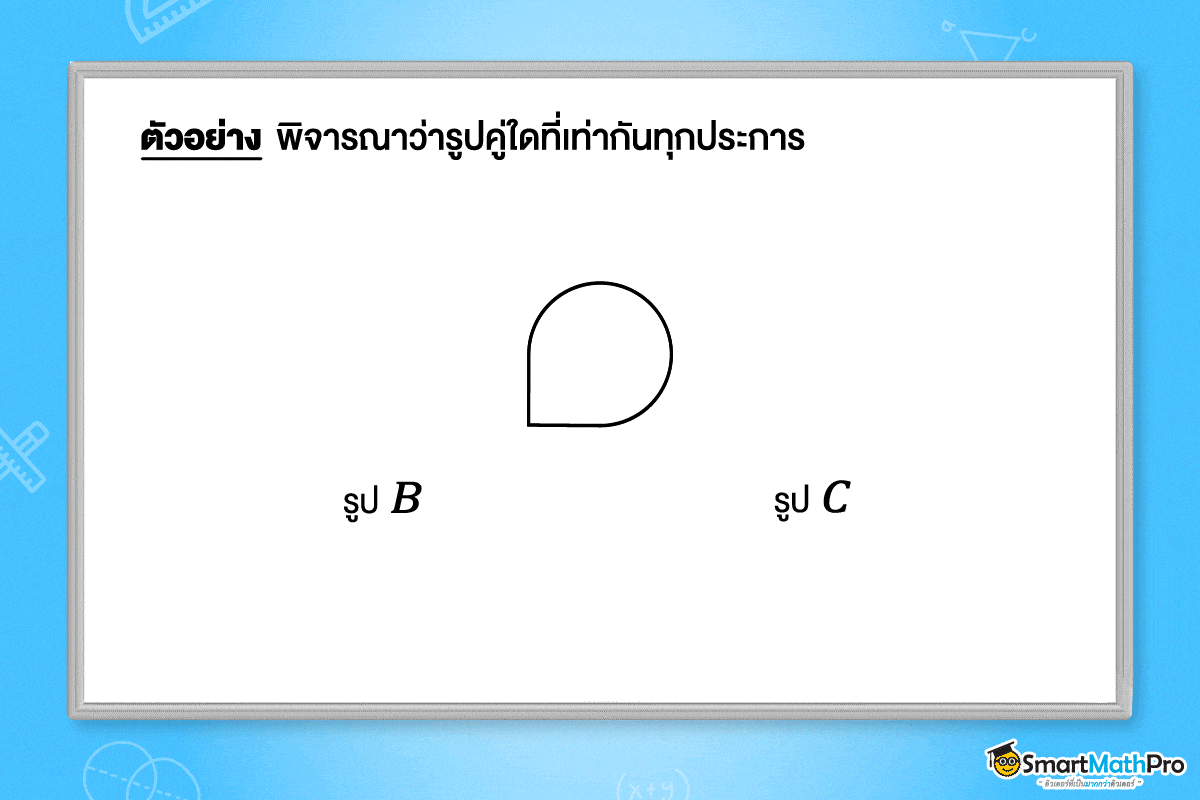
วิธีทำ จากรูปจะเห็นว่า รูป A $\cong$ รูป D และ รูป B $\cong$ รูป C เพราะสามารถใช้การแปลงทางเรขาคณิต ทำให้รูป A กับรูป D และรูป B กับรูป C เท่ากันทุกประการได้

ความเท่ากันทุกประการของรูปสามเหลี่ยม

รูปสามเหลี่ยมสองรูปเท่ากันทุกประการ ก็ต่อเมื่อด้านคู่ที่สมนัยและมุมคู่ที่สมนัยกันของรูปสามเหลี่ยมสองรูปนั้น
มีขนาดเท่ากันเป็นคู่ ๆ

ในการเขียนสัญลักษณ์แสดงรูปสามเหลี่ยมสองรูปที่เท่ากันทุกประการ เรานิยมเขียนตัวอักษรเรียงตามลำดับของมุมคู่ที่สมนัยกันและด้านคู่ที่สมนัยกัน ดังรูป

ตัวอย่างที่ 2 กำหนดให้ $\mathrm{\Delta\ ABC}\cong\mathrm{\Delta\ EDC}$ จงเขียนด้านคู่ที่สมนัยกันและมุมคู่ที่สมนัยกันของรูปสามเหลี่ยมคู่นี้

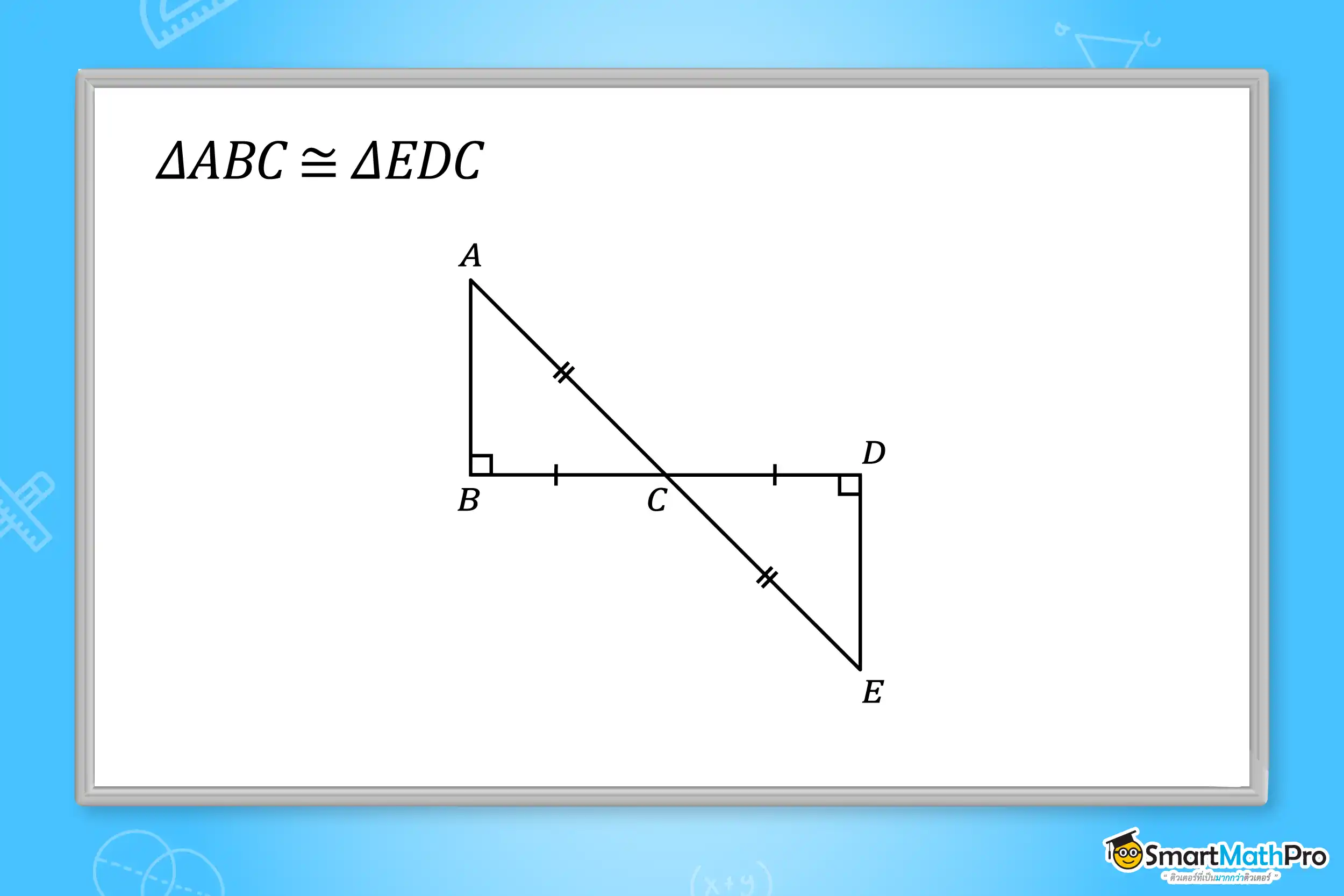
วิธีทำ จากรูป ด้านคู่ที่สมนัยกัน คือ $\bar{BC}$ กับ $\bar{DC},\ \bar{CA}$ กับ $\bar{CE}$ และ $\bar{AB}$ กับ $\bar{ED}$
มุมคู่ที่สมนัยกัน คือ $A\hat{B}C=E\hat{D}C,\ B\hat{C}A=D\hat{C}E$ และ $C\hat{A}B=C\hat{E}D$

ความสัมพันธ์แบบ ด้าน – มุม – ด้าน

เราจะเห็นว่าด้านที่ยาวเท่ากันต้องอยู่ระหว่างมุมที่มีขนาดเท่ากันสองคู่นั่นเอง เราลองไปทำความเข้าใจความสัมพันธ์นี้ผ่านตัวอย่างต่อไปนี้กันน

ตัวอย่างที่ 3 จากรูป กำหนดให้ $\mathrm{\Delta ABD}\cong\mathrm{\Delta CBD}$ ถ้า $A\hat{B}C=88°$ แล้วค่าของ $x$ เท่ากับเท่าใด

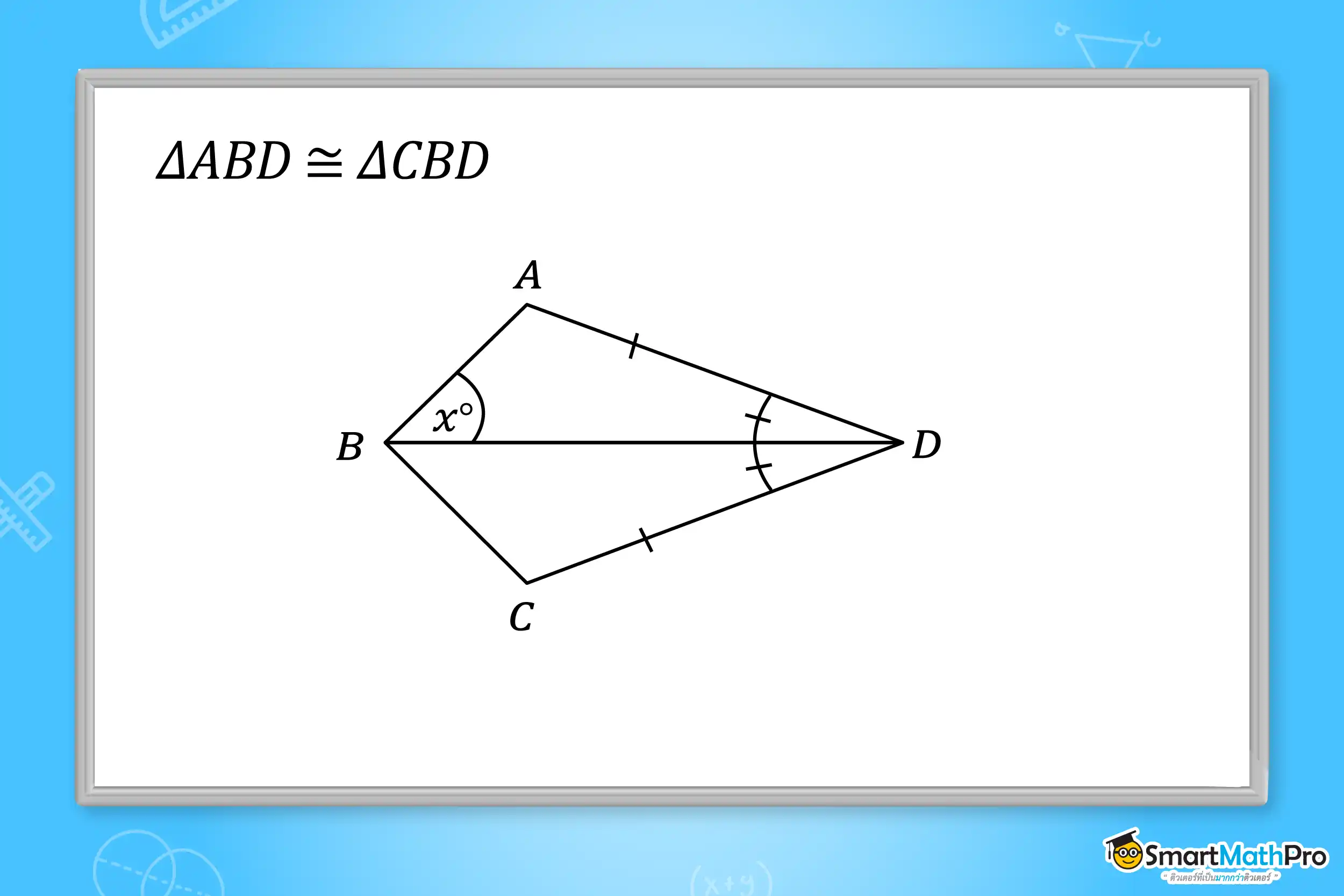
วิธีทำ จากรูป $AD=DC, A\hat{B}D=C\hat{B}D$ และ $BD=BD$ (เป็นด้านร่วม) ดังนั้น $\mathrm{\Delta ABD}\cong\mathrm{\Delta CBD}$ (ด้าน – มุม – ด้าน)

จะได้ว่า $A\hat{B}D=C\hat{B}D$ เนื่องจากเป็นมุมคู่ที่สมนัยกัน

จาก $A\hat{B}C=88°$

ดังนั้น $x\ =\ \frac{88}{2}\ =\ 44$

ความสัมพันธ์แบบ มุม – ด้าน – มุม

ตัวอย่างที่ 4 จากรูป กำหนดให้ $\mathrm{\Delta PQR}\cong\mathrm{\Delta STR}$ ถ้า $PR=7$ เซนติเมตร แล้วจงหา $RS$

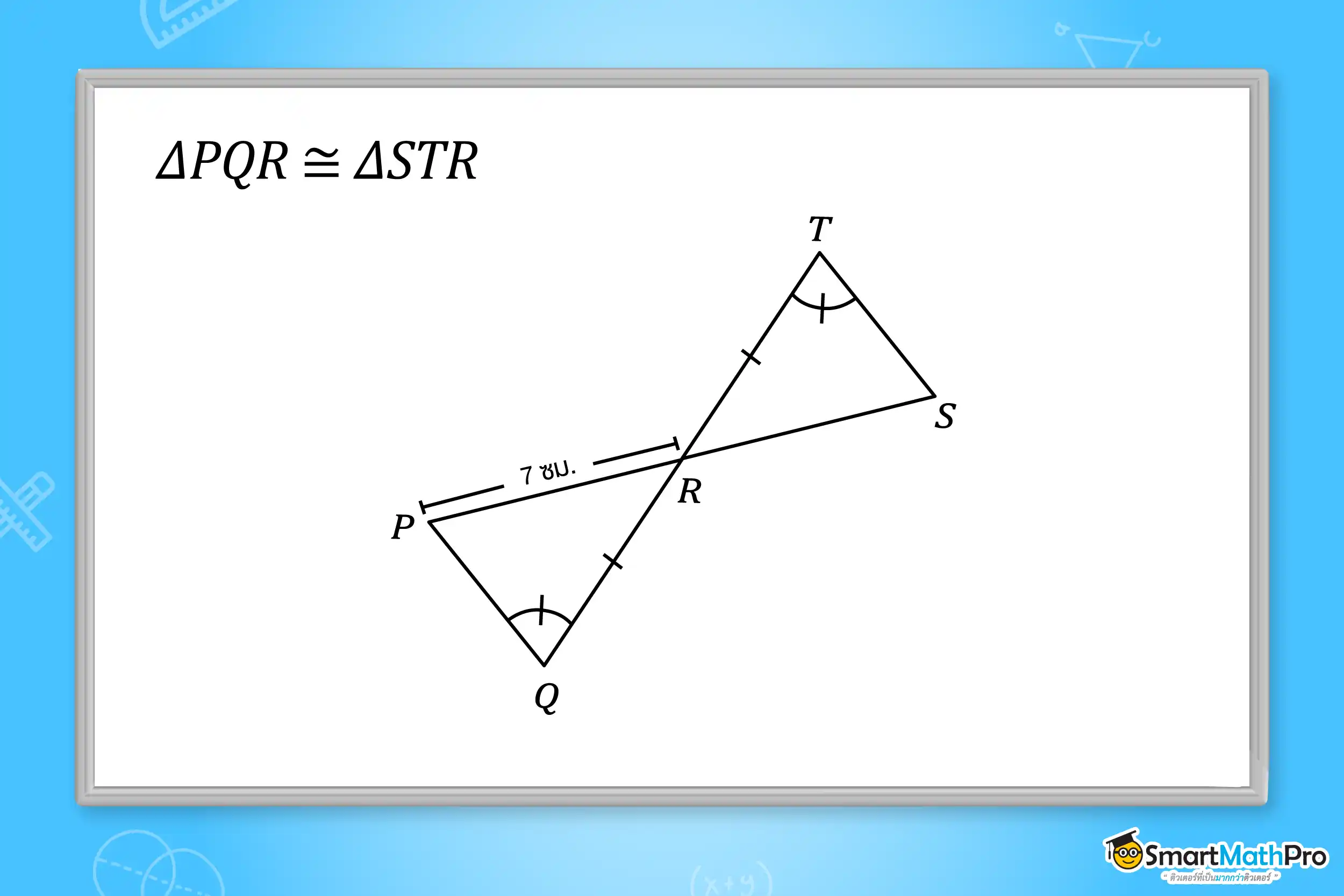
วิธีทำ จากรูป $S\hat{T}R=P\hat{Q}R, TR=QR$ และ $T\hat{R}S=Q\hat{R}P$ (เป็นมุมตรงข้าม)
ดังนั้น $\mathrm{\Delta PQR}\cong\mathrm{\Delta STR}$ (มุม – ด้าน – มุม)
จะได้ว่า $PR=RS$ เนื่องจากเป็นด้านคู่ที่สมนัยกัน
ดังนั้น $RS=7$ เซนติเมตร

ความสัมพันธ์แบบ ด้าน - ด้าน - ด้าน

รูปสามเหลี่ยมสองรูปที่เท่ากันทุกประการ จะมีความสัมพันธ์กันแบบ ด้าน – ด้าน – ด้าน แต่ไม่มีความสัมพันธ์กันแบบ
มุม – มุม – มุม น้า เพราะถึงแม้ขนาดของมุมทุกมุมเท่ากันเป็นคู่ ๆ แต่ความยาวด้านของแต่ละคู่อาจจะไม่เท่ากันก็ได้ ซึ่งจะทำให้รูปสามเหลี่ยมทั้งสองไม่เท่ากันทุกประการ แต่เราจะเรียกรูปสามเหลี่ยมคู่นั้นว่าสามเหลี่ยมคล้าย น้องจะได้เรียนเรื่องนี้ต่อไปในระดับชั้น ม.3 น้า เราลองไปทำความเข้าใจความสัมพันธ์แบบ ด้าน – ด้าน – ด้าน ผ่านตัวอย่างต่อไปนี้กันน

ตัวอย่างที่ 5 จากรูป กำหนดให้ $\mathrm{\Delta ABC}\cong\mathrm{\Delta BAE}$ จงหาขนาดของ $C\hat{A}B$

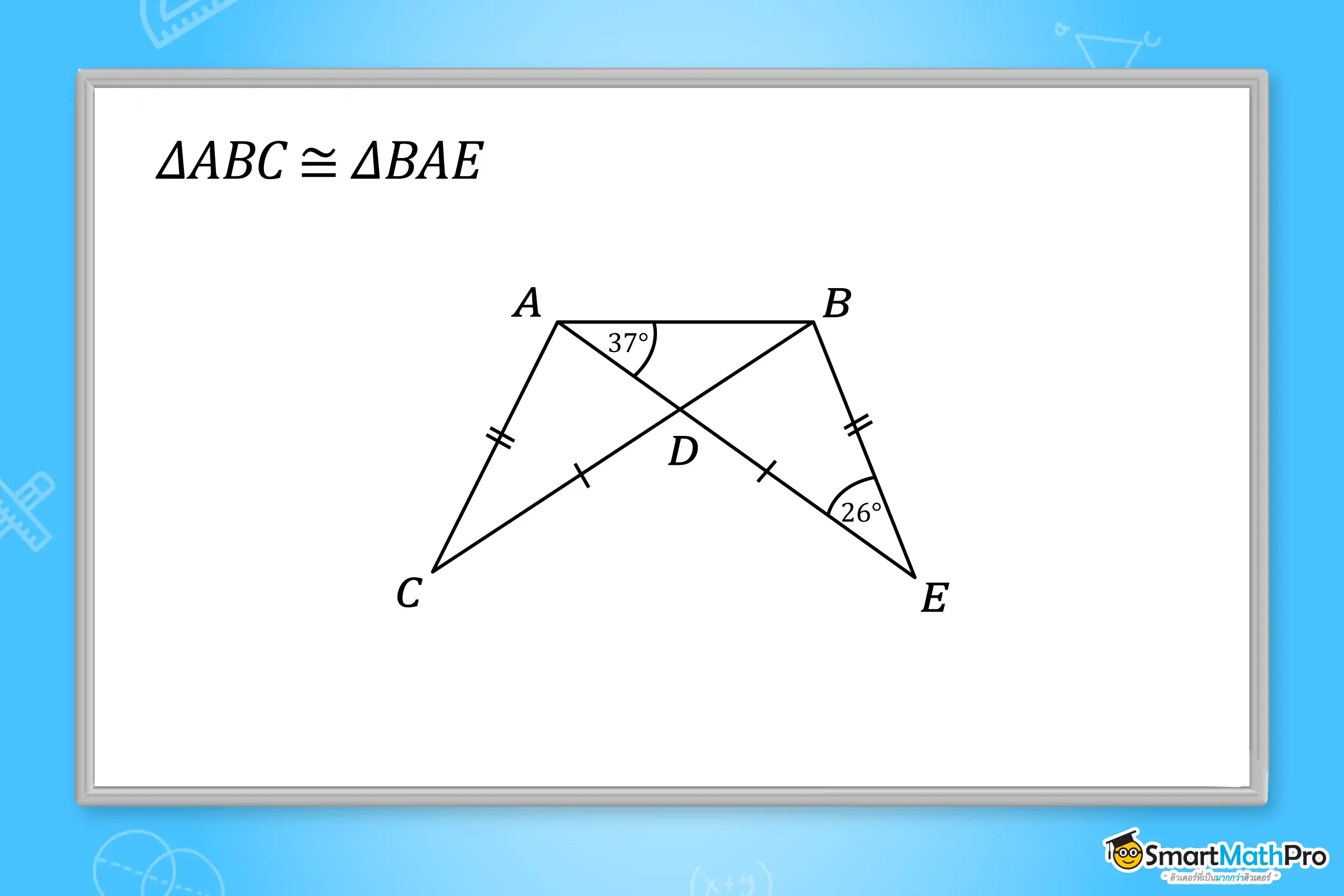
วิธีทำ จากรูป $AC=BE, BC=AE$ และ $AB=AB$ (เป็นด้านร่วม) ดังนั้น $\mathrm{\Delta ABC}\cong\mathrm{\Delta BAE}$ (ด้าน – ด้าน – ด้าน)
จะได้ว่า $C\hat{A}B=E\hat{B}A$ เนื่องจากเป็นมุมคู่ที่สมนัยกัน
พิจารณา $\mathrm{\Delta BAE}$ จากผลรวมของมุมภายในของรูปสามเหลี่ยมเท่ากับ 180 องศา
จะได้ $E\hat{B}A=180-37-26=117$ องศา
ดังนั้น $C\hat{A}B=117$ องศา

ความสัมพันธ์แบบ มุม - มุม - ด้าน

น้อง ๆ จะสังเกตได้ว่าความสัมพันธ์นี้ด้านคู่ที่เท่ากัน ต้องไม่อยู่ระหว่างมุมคู่สองมุม เพราะแบบนั้นจะเป็นความสัมพันธ์แบบ มุม – ด้าน – มุม ไม่ใช่ มุม – มุม – ด้าน นั่นเอง เราลองทำความเข้าใจความสัมพันธ์ผ่านตัวอย่างต่อไปนี้กัน

ตัวอย่างที่ 6 จากรูป กำหนดให้ $\mathrm{\Delta MNO}\cong\mathrm{\Delta QPO}$ ถ้า $MN=4$ เซนติเมตร และ $NO=3$ เซนติเมตร จงหาความยาวของส่วนของเส้นตรง $MQ$

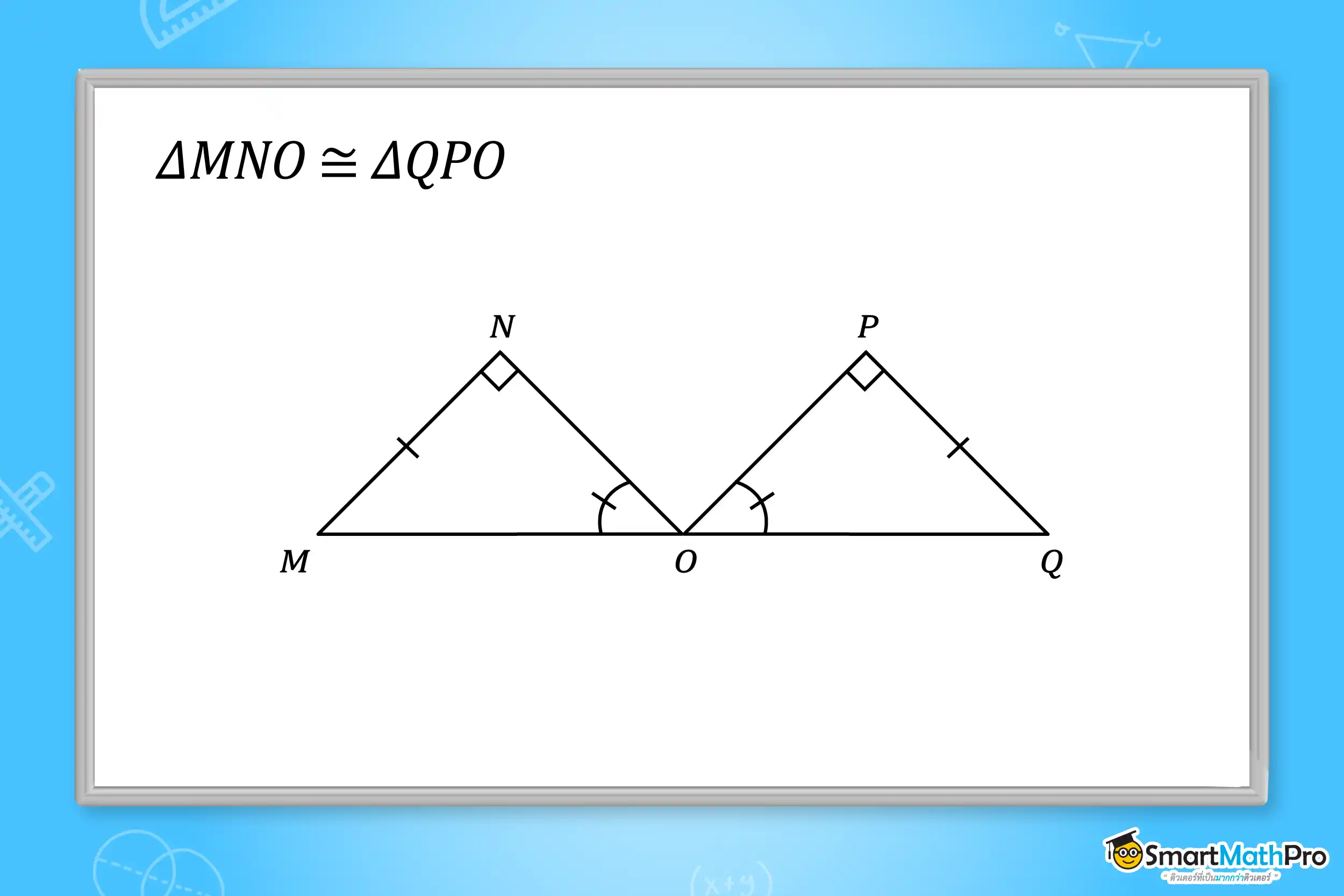
วิธีทำ จาก $\mathrm{\Delta MNO}$ เป็นรูปสามเหลี่ยมมุมฉาก
สามารถใช้ทฤษฎีบทพีทาโกรัสเพื่อหาความยาวของ $MO$ ได้
จะได้ว่า ${MO}^2=4^2+3^2=16+9=25$
$MO=-5,\ 5$ เนื่องจาก $MO$ เป็นความยาวด้าน
ดังนั้น $MO=5$ เซนติเมตร
จาก $\mathrm{\Delta MNO}\cong\mathrm{\Delta QPO}$ (มุม – มุม – ด้าน)
จะได้ว่า $MO=QO$ เนื่องจากเป็นด้านคู่ที่สมนัยกัน
ดังนั้น $QO=5$ เซนติเมตร
ดังนั้น $MQ=5+5=10$ เซนติเมตร

ความสัมพันธ์แบบ ฉาก - ด้าน - ด้าน

น้อง ๆ จะสังเกตได้ว่าความสัมพันธ์นี้ด้านคู่ที่เท่ากัน ต้องไม่เป็นแขนของมุมฉากทั้งสองด้าน เพราะแบบนั้นจะเป็นความสัมพันธ์แบบ ด้าน – มุม(ฉาก) – ด้าน ไม่ใช่ ฉาก-ด้าน-ด้าน นั่นเอง เราลองทำความเข้าใจความสัมพันธ์ผ่านตัวอย่าง
ต่อไปนี้กัน

ตัวอย่างที่ 7 จากรูป กำหนดให้ $\mathrm{\Delta ABC}\cong\mathrm{\Delta DCB}$ จงหาขนาดของมุม $BEC$

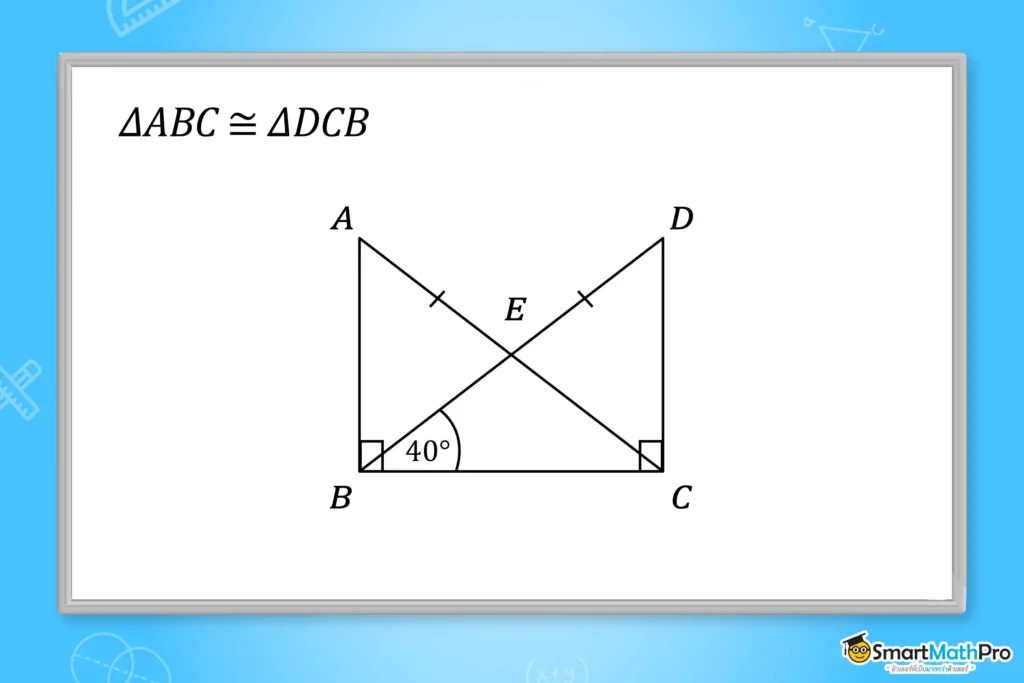
วิธีทำ จากรูป $A\hat{B}C=D\hat{C}B=90°, AC=DB$ และ $BC=BC$ (เป็นด้านร่วม) ดังนั้น $\mathrm{\Delta ABC}\cong\mathrm{\Delta DCB}$ (ฉาก – ด้าน – ด้าน)
จะได้ว่า $A\hat{C}B=D\hat{B}C$ เนื่องจากเป็นมุมคู่ที่สมนัยกัน
ดังนั้น $D\hat{B}C=40°=A\hat{C}B$
พิจารณา $\mathrm{\Delta}BEC$
นั่นคือ $B\hat{E}C=180-40-40=100$ องศา

การนำความเท่ากันทุกประการไปใช้

ในบทนี้ เราจะนำความรู้เรื่องความเท่ากันทุกประการไปประยุกต์ใช้กับรูปสามเหลี่ยมหน้าจั่ว โดยบทนิยามของรูปสามเหลี่ยมหน้าจั่ว คือ

บทนิยาม
รูปสามเหลี่ยมหน้าจั่ว (isosceles triangle) คือ รูปสามเหลี่ยมที่มีด้านสองด้านยาวเท่ากัน

สมบัติของรูปสามเหลี่ยมหน้าจั่วที่จะได้เรียนในบทนี้มีทั้งหมด 5 ข้อ ดังนี้

เส้นแบ่งครึ่งมุมยอดของรูปสามเหลี่ยมหน้าจั่ว จะแบ่งรูปสามเหลี่ยมหน้าจั่วออกเป็นรูปสามเหลี่ยมสองรูปที่เท่ากันทุกประการ
มุมที่ฐานของรูปสามเหลี่ยมหน้าจั่วมีขนาดเท่ากัน
เส้นแบ่งครึ่งมุมยอดของสามเหลี่ยมหน้าจั่ว จะแบ่งครึ่งฐานของรูปสามเหลี่ยมหน้าจั่ว และจะตั้งฉากกับฐานของรูปสามเหลี่ยมหน้าจั่ว
เส้นที่ลากจากมุมยอดของรูปสามเหลี่ยมหน้าจั่วมาแบ่งครึ่งฐาน จะแบ่งครึ่งมุมยอดของสามเหลี่ยมหน้าจั่ว และจะตั้งฉากกับฐานของรูปสามเหลี่ยมหน้าจั่ว
เส้นที่ลากจากมุมยอดของรูปสามเหลี่ยมหน้าจั่วมาตั้งฉากกับฐาน จะแบ่งครึ่งมุมยอดของสามเหลี่ยมหน้าจั่ว และจะแบ่งครึ่งฐานของรูปสามเหลี่ยมหน้าจั่ว

เราสามารถนำสมบัติด้านบนนี้ไปใช้เพื่ออ้างอิงในการแก้โจทย์ต่าง ๆ ได้ เพื่อให้เข้าใจมากขึ้น ลองไปใช้สมบัติของรูปสามเหลี่ยมหน้าจั่วผ่านโจทย์ต่อไปนี้กัน

ตัวอย่างที่ 8 จากรูป กำหนดให้รูปสามเหลี่ยม $ABD$ เป็นรูปสามเหลี่ยมหน้าจั่ว ถ้า $AC=10$ เซนติเมตร แล้วพื้นที่ของรูปสามเหลี่ยม $ACE$ เท่ากับเท่าใด

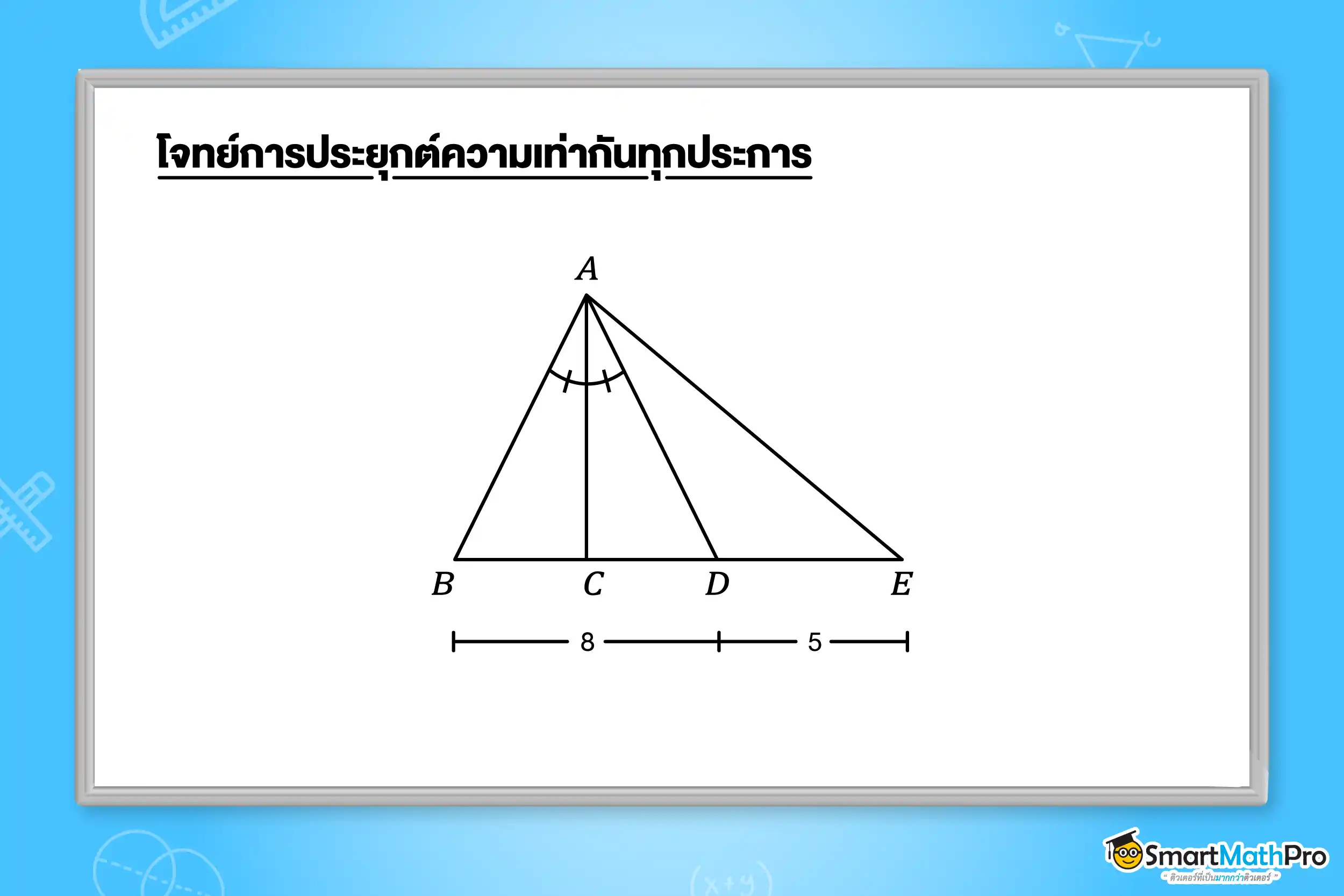
วิธีทำ จากรูป $\overline{AC}$ เป็นเส้นแบ่งครึ่งมุมยอดของรูปสามเหลี่ยมหน้าจั่ว $ABD$ ซึ่งจะแบ่งครึ่งฐานของรูปสามเหลี่ยมหน้าจั่ว และจะตั้งฉากกับฐานของรูปสามเหลี่ยมหน้าจั่ว
จะได้ว่า $AC\bot\ BD$
จาก $BD=8$ เซนติเมตร จะได้ $BC=CD=4$ เซนติเมตร
ดังนั้น $CE = 4+5=9$ เซนติเมตร
จาก $AC\bot\ BD$ และ $B, C, D, E$ เป็นจุดบนเส้นตรงเดียวกัน
จะได้ว่า $AC\bot CE$
ดังนั้น พื้นที่ของรูปสามเหลี่ยม $ACE=\frac{1}{2}\times CE\times AC=\frac{1}{2}\times9\times10=45$ ตารางเซนติเมตร

ติวคณิตศาสตร์ ม.ต้น กับ SmartMathPro

สำหรับน้อง ๆ ม.2 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์

พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.2 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน แนวข้อสอบเข้าม.4 และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก เลย

อ่านกันมาจนถึงตรงนี้ พี่คิดว่าน้อง ๆ น่าจะเข้าใจเรื่องความเท่ากันทุกประการ ม.2 กันมากขึ้นแล้ว โดยพี่แนะนำให้ทำแบบฝึกหัดเรื่องนี้บ่อย ๆ เพราะจะช่วยให้แม่นยำในเนื้อหามากขึ้น ซึ่งนอกจากตัวอย่างโจทย์ให้ดูในบทความนี้แล้ว พี่ยังมีแบบฝึกหัดให้ลองทำเพิ่มเติมด้วยน้าา >> แบบฝึกหัดความเท่ากันทุกประการ ม.2