สำหรับน้อง ๆ ม.ปลายที่กำลังมองหาสรุปเนื้อหาฟิสิกส์ ม.5 เรื่องไฟฟ้าสถิต ไม่ควรพลาดบทความนี้เลยน้าา เพราะว่าพี่เตรียมสรุปทั้งความหมาย สาเหตุการเกิดไฟฟ้าสถิต ประจุไฟฟ้า กฎของคูลอมบ์ และยังมีหัวข้อที่น่าสนใจอื่น ๆ อีกเพียบ
และเพื่อเสริมความเข้าใจให้น้อง ๆ มากขึ้น พี่มีตัวอย่างโจทย์ให้น้อง ๆ ดูในแต่ละหัวข้อพร้อมแจกแบบฝึกหัดและเฉลยให้ท้ายบทความด้วยน้าา
ไฟฟ้าสถิต (Static Electricity) คือ ปรากฏการณ์ที่เกิดขึ้นจากความไม่สมดุลของประจุไฟฟ้าภายในวัตถุ
เมื่อวัตถุมีประจุบวกหรือลบสะสมอยู่มากเกินไป โดยไม่มีการไหลของกระแสไฟฟ้าเหมือนในวงจรไฟฟ้าทั่วไป
ประจุเหล่านี้จะคงอยู่กับที่ (static) จนกว่าจะมีการถ่ายเทหรือเคลื่อนย้ายไปยังวัตถุอื่น ซึ่งเรียกว่า การถ่ายเทประจุ
(Electrostatic Discharge: ESD)
หนึ่งในตัวอย่างใกล้ตัวที่สุดของไฟฟ้าสถิต คือ เวลาที่เราเดินบนพรมแล้วไปแตะลูกบิดประตู
แล้วรู้สึก “ช็อต” เล็ก ๆ — นั่นคือการถ่ายเทประจุไฟฟ้าสถิตจากร่างกายไปยังโลหะที่มีประจุต่างกัน
ปรากฏการณ์ไฟฟ้าสถิตสามารถแบ่งออกได้เป็น 3 ลักษณะหลัก ได้แก่
1. การดึงดูด (Attraction) เมื่อวัตถุมีประจุต่างขั้วกัน เช่น วัตถุที่มีประจุบวกเข้าใกล้วัตถุที่มีประจุลบ จะเกิดแรงดึงดูดกัน เช่น การใช้หวีพลาสติกที่เพิ่งหวีผมดูดเศษกระดาษเล็ก ๆ ได้
2. การผลักกัน (Repulsion) เมื่อวัตถุทั้งสองมีประจุชนิดเดียวกัน เช่น ลบกับลบ หรือ บวกกับบวก จะผลักกันออก
เช่น เมื่อเราใช้ลูกโป่งถูผม แล้วนำลูกโป่งไปใกล้อีกลูกหนึ่งที่ถูกถูมาเช่นกัน จะเห็นว่าลูกโป่งจะผลักกัน
3. การเกิดประกายไฟฟ้า (Electric Spark) เมื่อประจุไฟฟ้าที่สะสมไว้ในวัตถุถูกถ่ายเทออกอย่างรวดเร็ว จะเกิดประกายไฟหรือเสียงแปล็บเล็ก ๆ ซึ่งเกิดจากการเคลื่อนที่อย่างฉับพลันของอิเล็กตรอน เช่น เวลาสัมผัสลูกบิดประตู
หรือถอดเสื้อผ้าที่ทำจากใยสังเคราะห์
ประจุไฟฟ้า (Electric Charge)
ประจุไฟฟ้า (Electric Charge) คือ คุณสมบัติพื้นฐานของอนุภาคมูลฐานที่ทำให้เกิดแรงระหว่างกันเมื่ออยู่ภายใต้สนามไฟฟ้าหรือสนามแม่เหล็ก โดยสนามเหล่านี้มีอิทธิพลต่ออนุภาคที่มีประจุแต่ละชนิดต่างกัน
วัตถุต่าง ๆ ประกอบด้วยอะตอมจำนวนมาก ภายในอะตอมประกอบด้วยอนุภาคมูลฐาน ดังนี้
- โปรตอน (Proton): มีประจุไฟฟ้าเป็นบวก และอยู่ในนิวเคลียส
- นิวตรอน (Neutron): ไม่มีประจุไฟฟ้า (เป็นกลาง) อยู่ในนิวเคลียสเช่นกัน
- อิเล็กตรอน (Electron): มีประจุไฟฟ้าเป็นลบ เคลื่อนที่อยู่รอบนิวเคลียสในวงโคจร
มวลของอิเล็กตรอนมีค่าต่ำกว่าของโปรตอนและนิวตรอนอย่างมาก แต่ประจุของอิเล็กตรอนมีขนาดเท่ากับโปรตอนใน
ทางขนาด (แต่มีขั้วตรงข้าม)
สภาพทางไฟฟ้าของวัตถุบอกได้จาก “ประจุสุทธิของวัตถุ”
- วัตถุที่มีประจุบวก (+) คือ วัตถุที่มีจำนวนโปรตอนมากกว่าอิเล็กตรอน หรือ สูญเสียอิเล็กตรอน
- วัตถุที่มีประจุลบ (−) คือ วัตถุที่มีจำนวนอิเล็กตรอนมากกว่าโปรตอน หรือ ได้รับอิเล็กตรอน
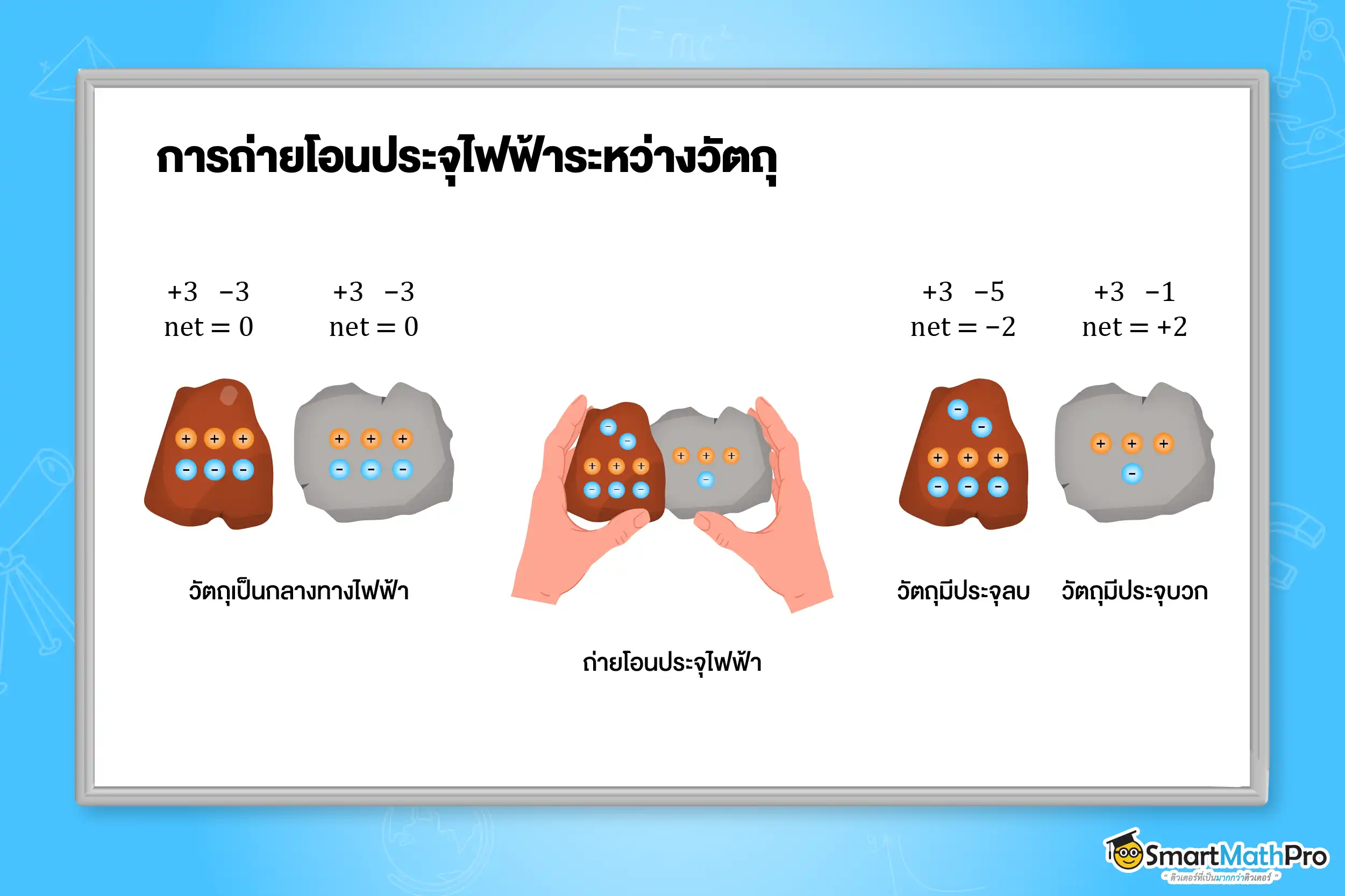
ในสภาวะปกติ วัตถุจะมีโปรตอนและอิเล็กตรอนเท่ากัน ทำให้มีสภาพเป็นกลางทางไฟฟ้า แต่เมื่อมีการถ่ายโอนอิเล็กตรอน เช่น จากการเสียดสี การเหนี่ยวนำ หรือการสัมผัส จะทำให้วัตถุเกิดประจุไฟฟ้า โดยการถ่ายโอนนี้เป็นไปตามกฎอนุรักษ์ประจุไฟฟ้า กล่าวคือ “ปริมาณประจุไฟฟ้ารวมของระบบก่อนและหลังการถ่ายโอนจะมีค่าเท่าเดิม”
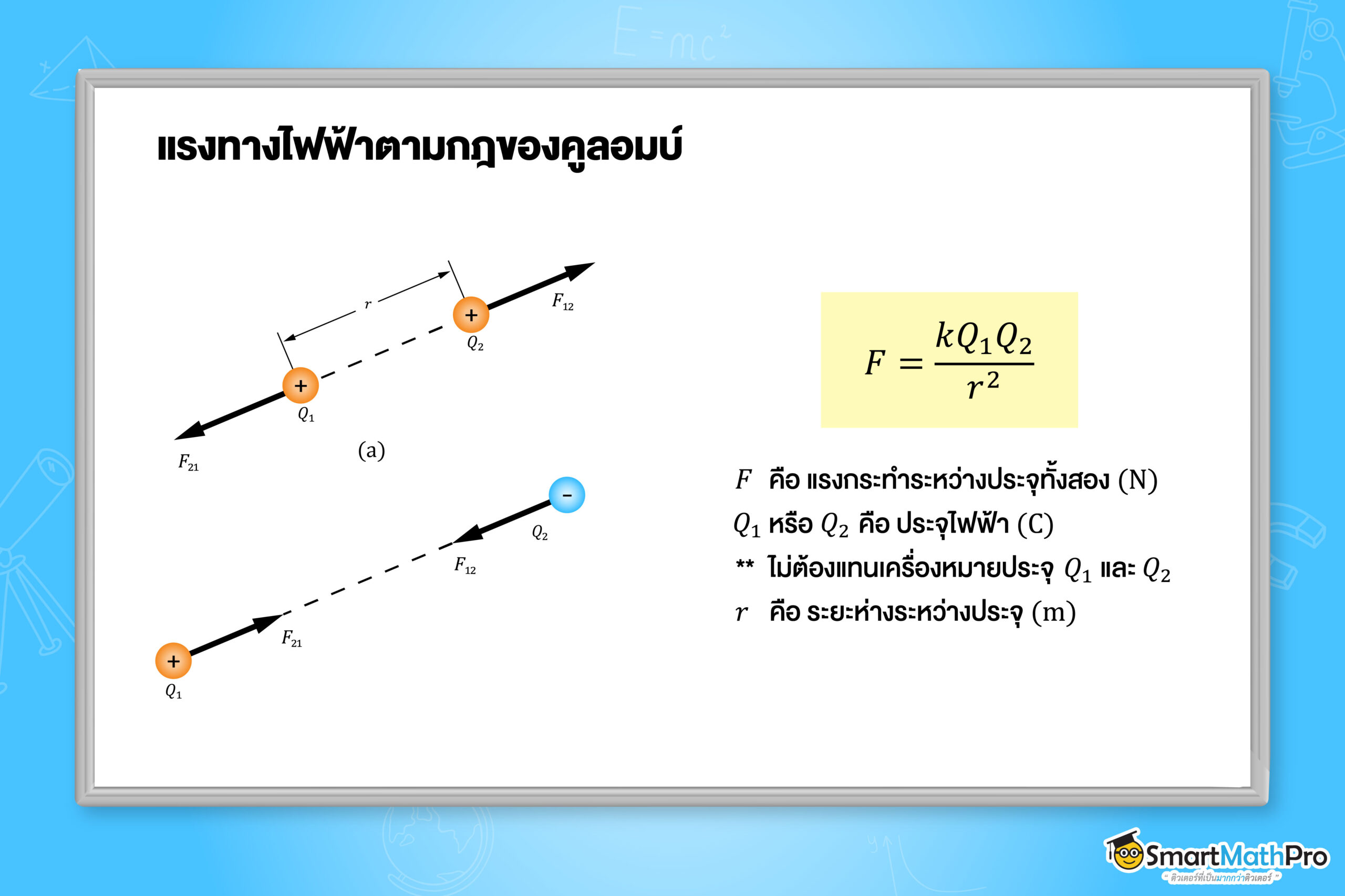
กฎของคูลอมบ์ (Coulomb’s Law)
เป็นกฎที่อธิบายแรงกระทำระหว่างประจุคู่หนึ่ง โดยขนาดของแรงขึ้นกับระยะห่าง และปริมาณประจุไฟฟ้า แรงกระทำระหว่างประจุมีสองแบบ คือ
- แรงดูด คือ แรงกระทำระหว่างประจุต่างกัน (บวกและลบ)
- แรงผลัก คือ แรงกระทำระหว่างประจุชนิดเดียวกัน (บวกทั้งคู่ หรือ ลบทั้งคู่)
ข้อควรรู้เกี่ยวกับกฎของคูลอมบ์
- ค่าคงที่ของคูลอมบ์ในสุญญากาศ k=\frac{1}{4\pi\varepsilon _{0} }\approx 9\times 10^{9}Nm^{2}/C^{2}
- ค่าสภาพยอมในสุญญากาศ \varepsilon _{0}=8.854\times 10^{-12}C^{2}/Nm^{2} สื่อถึงความสามารถในการส่งแรงไฟฟ้าในสุญญากาศ สำหรับสภาพแวดล้อมอื่นแรงไฟฟ้าจะสามารถถูกส่งได้น้อยลง
- แรงไฟฟ้าเป็นไปตามกฎข้อที่ 3 ของนิวตัน กล่าวคือ เป็นแรงคู่กิริยา – ปฏิกิริยา
จุดประจุ -4\mu C วางห่างจากจุดประจุ -2\mu C และ +3\mu C ดังรูป
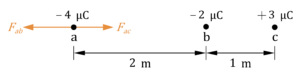
จงหาแรงลัพธ์ที่กระทำกับจุดประจุ -4\mu C
วิธีทำ หาแรงที่ประจุ b กระทำต่อประจุ a
F_{ab}=\frac{kQ_{a}Q_{b}}{r_{ab}^{2}}
F_{ab}=\frac{9\times 10^{9}(4\times 10^{-6})(2\times10^{-6})}{2^{2}}
F_{ab}=18\times 10^{-3}N
หาแรงที่ประจุ c กระทำต่อประจุ a
F_{ac}=\frac{kQ_{a}Q_{c}}{r_{ac}^{2}}
F_{ac}=\frac{9\times 10^{9}(4\times 10^{-6})(3\times10^{-6})}{3^{2}}
F_{ac}=12\times 10^{-3}N
หาแรงลัพธ์กระทำต่อประจุ a
\sum F=F_{ac}-F_{ab}
\sum F=12\times 10^{-3}-18\times 10^{-3}
\sum F=-6\times 10^{-3}
ตอบ แรงลัพธ์ที่กระทำกับจุดประจุ -4\mu C เท่ากับ 6\times 10^{-3} นิวตัน ไปทาง -x
สนามไฟฟ้า (Electric Field)
สนามไฟฟ้า (Electric Field) คือ บริเวณที่มีอำนาจทางไฟฟ้ากระทำต่อวัตถุที่มีประจุไฟฟ้า ซึ่งสนามไฟฟ้า คือ แรงที่กระทำต่อประจุ +1 หน่วย (คูลอมบ์) เป็นปริมาณเวกเตอร์ ซึ่งมีทิศทางเดียวกับแรงที่กระทำต่อประจุบวกที่จุดนั้น ๆ สามารถเขียนเป็นสมการความสัมพันธ์ระหว่างแรงกับสนามไฟฟ้าได้เป็น
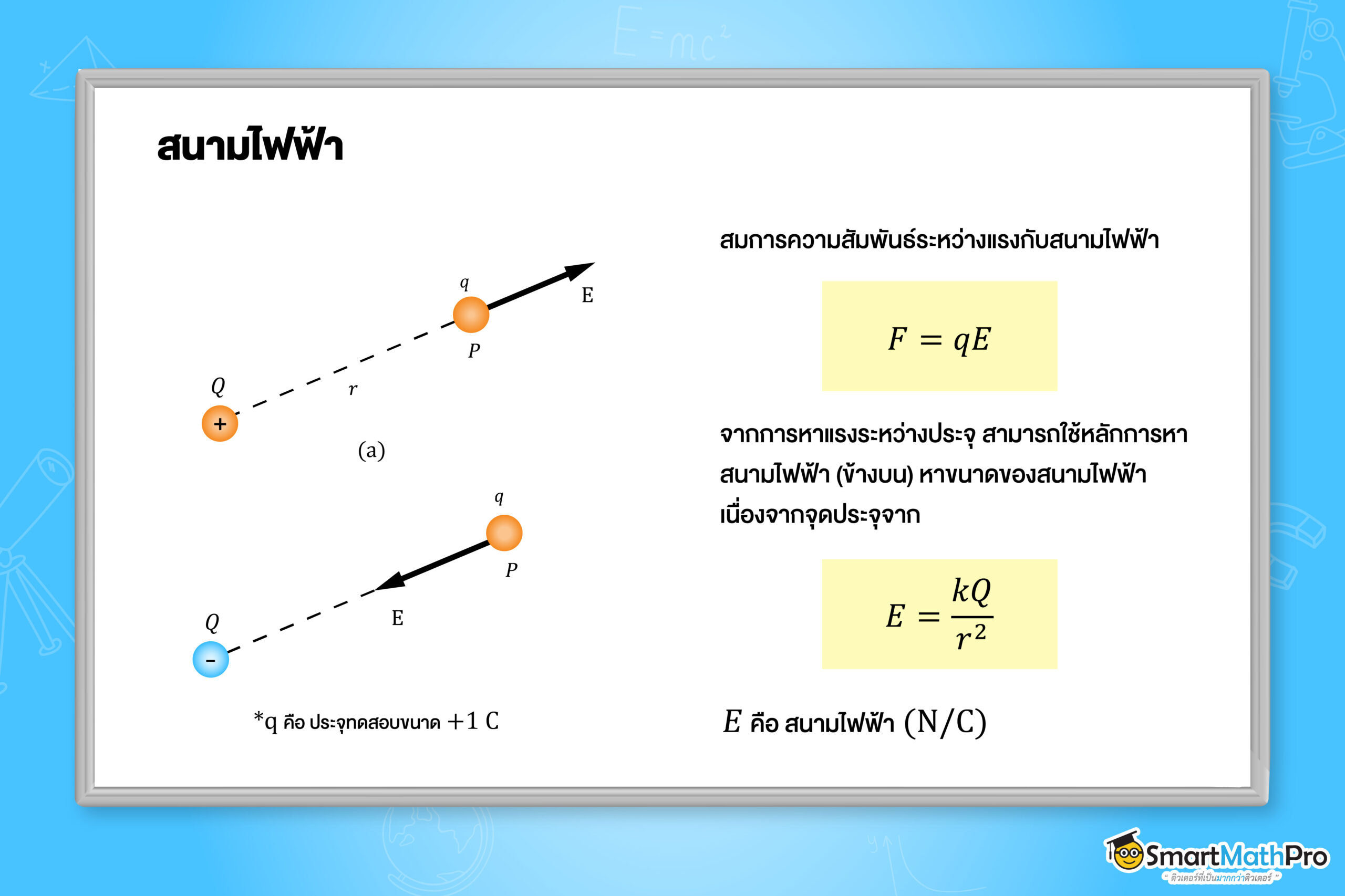
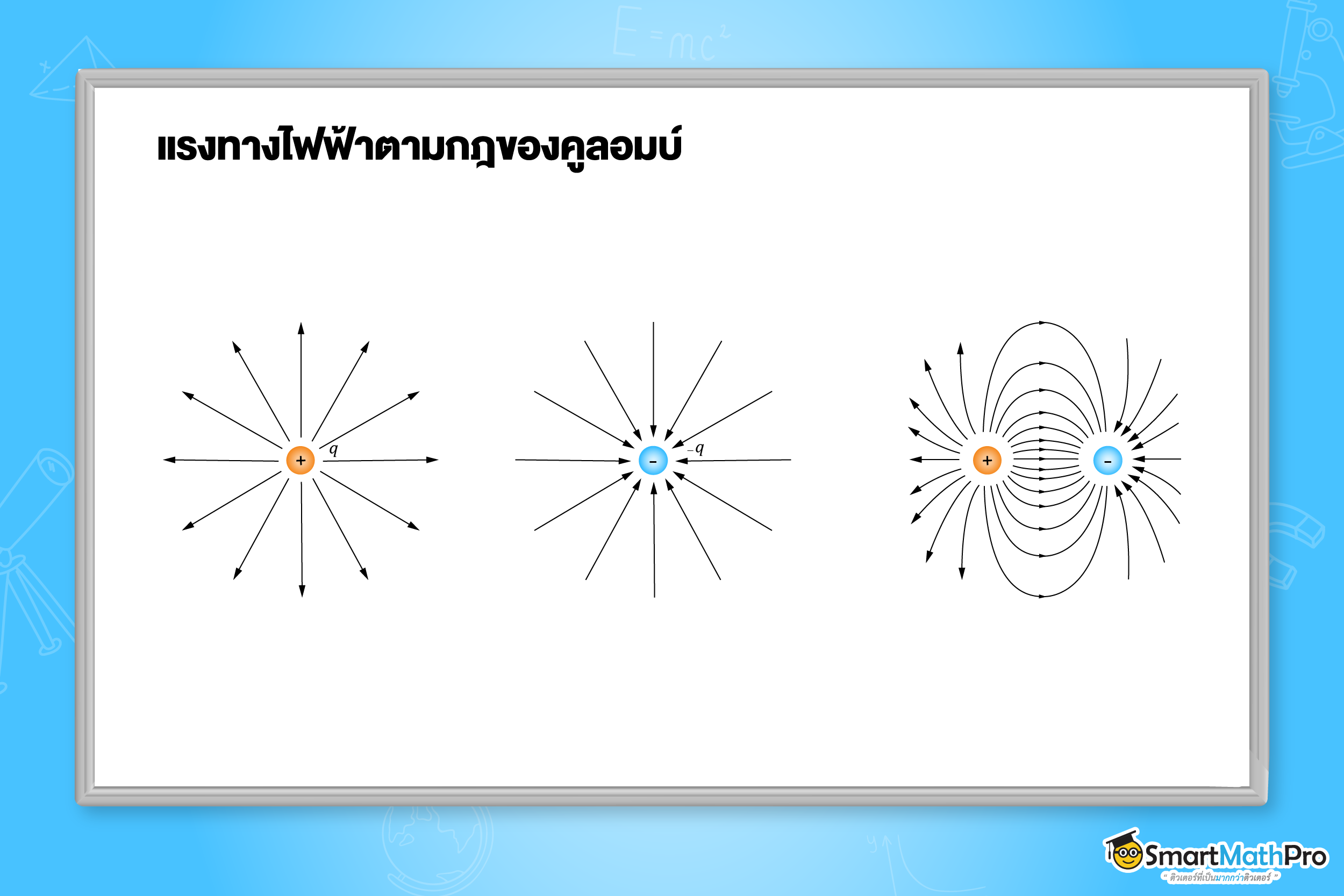
เส้นแรงทางไฟฟ้า
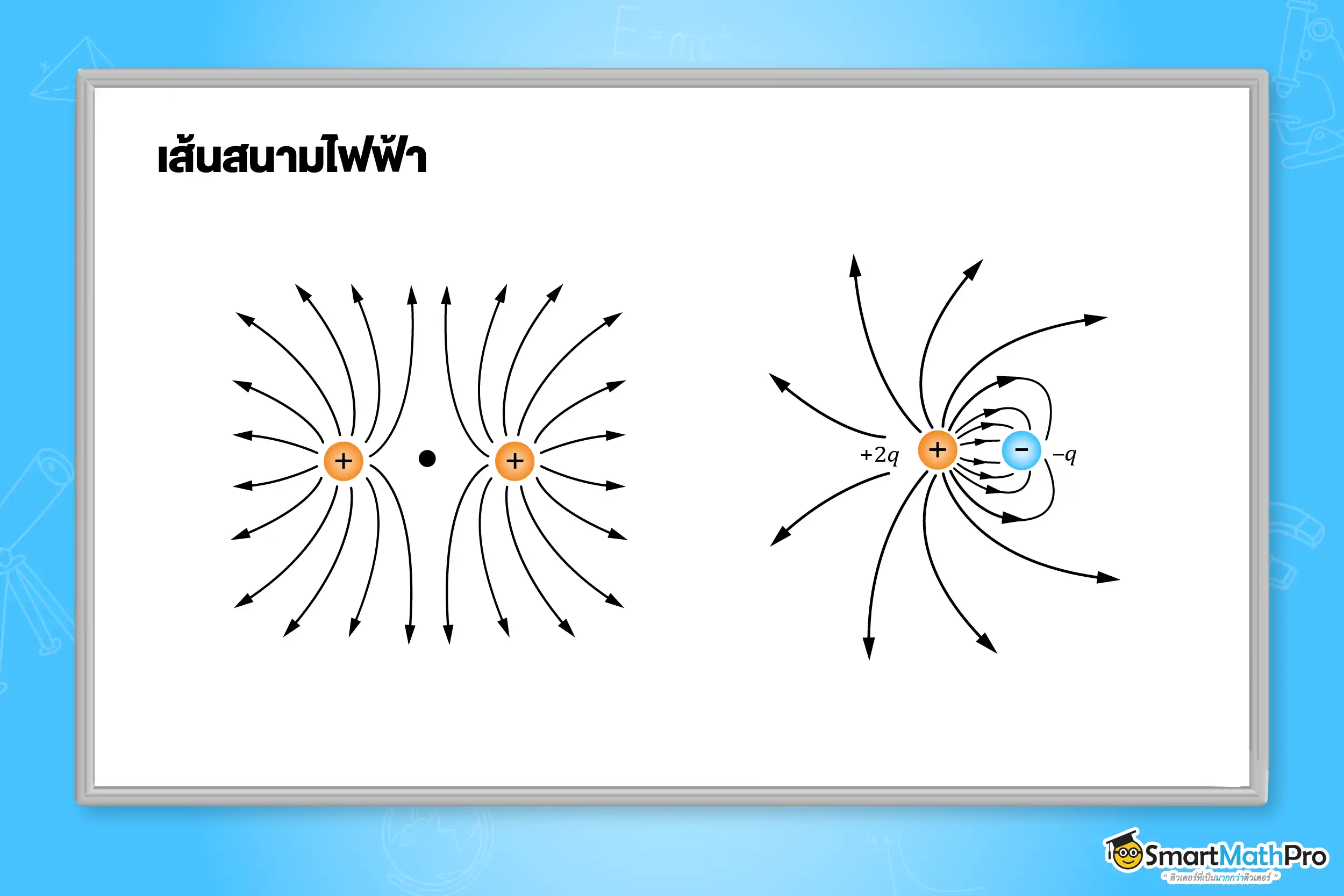
เส้นแรงทางไฟฟ้า คือ เส้นที่แสดงถึงแนวของแรงไฟฟ้า มีทิศพุ่งออกจากประจุบวกและมีทิศทางพุ่งเข้าประจุลบ โดยเส้นแรงไฟฟ้าจะไม่ตัดกันเลย
จุดประจุ 2 ตัว วางห่างดังภาพ จงหาสนามไฟฟ้าที่จุด X
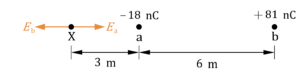
วิธีทำ
หาสนามไฟฟ้าลัพธ์ที่จุด X
E_{X}=E_{a}-E_{b}
E_{X}=\frac{kQ_{a}}{r_{a}^{2}}-\frac{kQ_{b}}{r_{b}^{2}}
E_{X}=\frac{9\times 10^{9}(18\times10^{-9})}{(3\times 10^{-2})^{2}}-\frac{9\times 10^{9}(81\times10^{-9})}{(9\times 10^{-2})^{2}}
E_{X}=9\times 10^{4}N/C
ตอบ สนามไฟฟ้าที่จุด X เท่ากับ 9\times 10^{4}N/C
จุดสะเทินในสนามไฟฟ้า
จุดสะเทินในสนามไฟฟ้า คือ จุดที่สนามไฟฟ้าลัพธ์หรือผลลัพธ์ของสนามไฟฟ้ามีค่าเท่ากับศูนย์
ในกรณีที่มีสนามไฟฟ้าสองสนาม จากประจุไฟฟ้า 2 ประจุวางใกล้กัน จุดสะเทินที่เกิดขึ้นจะอยู่ในแนวเส้นตรงที่ผ่านประจุไฟฟ้าทั้งสองนั้น ดังนี้
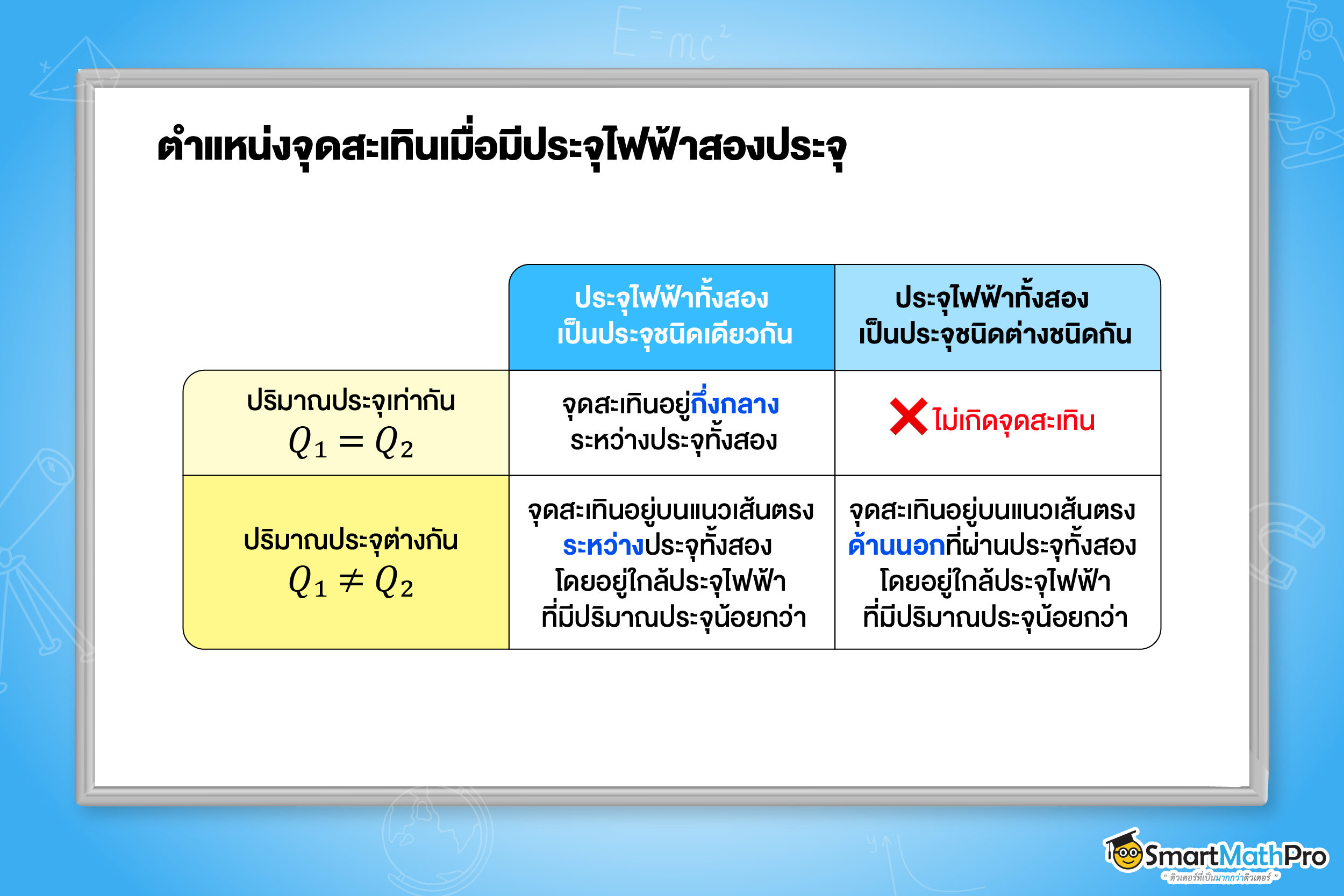
ข้อที่ 1
จุดประจุ + 3 ไมโครคูลอมบ์ และ + 12 ไมโครคูลอมบ์ วางห่างกัน 3 เมตร ตำแหน่งของจุดสะเทินจะอยู่ห่างจากจุดประจุ + 3 ไมโครคูลอมบ์เท่าใด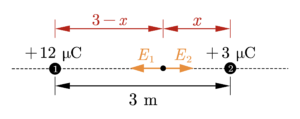
วิธีทำ
จุดสะเทินจะอยู่บนแนวเส้นตรงระหว่างประจุทั้งสอง โดยอยู่ใกล้กับประจุ +3 ไมโครคูลอมบ์ เป็นระยะ x เมตร
E_{1}=E_{2}
\frac{kQ_{1}}{r_{1}^{2}}=\frac{kQ_{2}}{r_{2}^{2}}
\frac{12\times 10^{-6}}{(3-x)^{2}}=\frac{3\times 10^{-6}}{x^{2}}
\frac{(3-x)^{2}}{x^{2}}=\frac{12\times 10^{-6}}{3\times 10^{-6}}
\frac{3-x}{x}=2
3-x=2x
x=1
ตอบ ตำแหน่งของจุดสะเทินจะอยู่ระหว่างประจุทั้งสอง โดยอยู่ห่างจากจุดประจุ +3 ไมโครคูลอมบ์ เป็นระยะ 1 เมตร
ข้อที่ 2
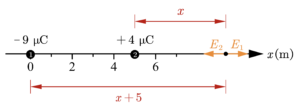
จุดประจุ +4 ไมโครคูลอมบ์ วางไว้บนแกน xกับประจุ -9 ไมโครคูลอมบ์ ดังภาพ จงหาตำแหน่ง x ที่เกิดจุดสะเทิน
วิธีทำ
จุดสะเทินอยู่บนแนวเส้นตรงด้านนอกที่ผ่านประจุทั้งสอง โดยอยู่ใกล้กับประจุ +4 ไมโครคูลอมบ์ เป็นระยะ x เมตร
E_{1}=E_{2}
\frac{kQ_{1}}{r_{1}^{2}}=\frac{kQ_{2}}{r_{2}^{2}}
\frac{9\times 10^{-6}}{(5+x)^{2}}=\frac{4\times 10^{-6}}{x^{2}}
\frac{(5+x)^{2}}{x^{2}}=\frac{9\times 10^{-6}}{4\times 10^{-6}}
\frac{5+x}{x}=\frac{3}{2}
10+2x=3x
x=10
ตอบ ตำแหน่ง x ที่เกิดจุดสะเทินเท่ากับ 10+5=15 เมตร
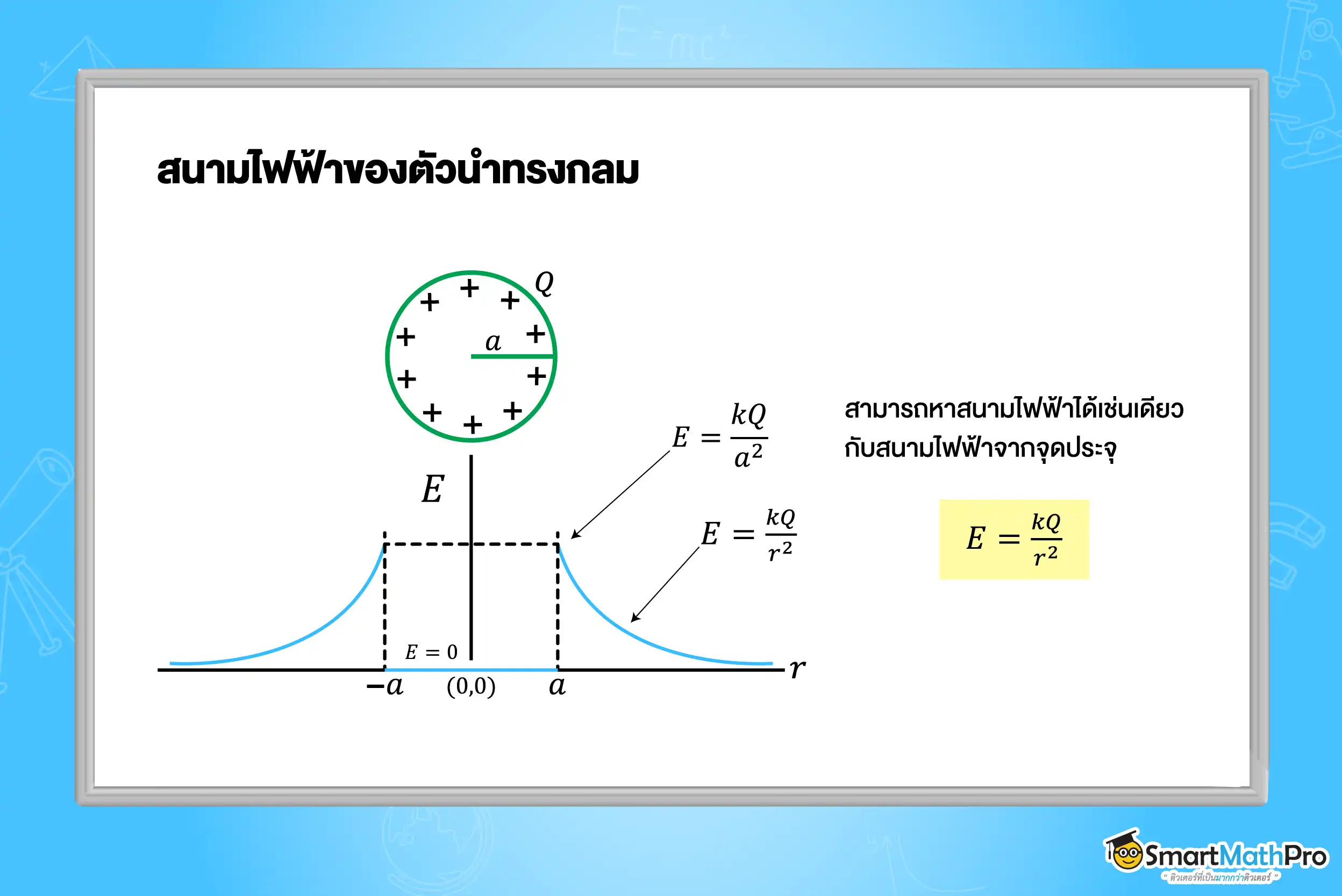
สนามไฟฟ้าของตัวนำทรงกลม
เนื่องจากภายในตัวนำไม่มีประจุ (ประจุกระจายอยู่เฉพาะผิวนอก) เมื่อนำประจุทดสอบ +1 คูลอมบ์ไปวางภายในตัวนำจะไม่เกิดแรงไฟฟ้ากระทำต่อประจุทดสอบ จึงไม่มีสนามไฟฟ้า ณ ตำแหน่งนั้น หรือสนามไฟฟ้ามีค่าเป็นศูนย์
และที่ผิวทรงกลมจะมีความเข้มของสนามไฟฟ้ามากที่สุด
ศักย์ไฟฟ้าและความต่างศักย์ (Electric Potential)
ศักย์ไฟฟ้า (Electric Potential) เนื่องจากจุดประจุ
ศักย์ไฟฟ้า ณ จุดใด ๆ ในสนามไฟฟ้า คือ ปริมาณงานจากแรงภายนอกที่ต้องใช้ในการนำประจุทดสอบบวกขนาดหนึ่งหน่วยจากระยะอนันต์ มายังจุดนั้น ศักย์ไฟฟ้าเป็นปริมาณสเกลาร์ โดยมีสูตรคำนวณดังนี้
V=\frac{kQ}{R}
โดยที่
V คือ ศักย์ไฟฟ้า (Electric Potential) หน่วย โวลต์ (V)
k คือ ค่าคงที่ของคูลอมบ์ (Coulomb’s Constant) ค่าประมาณ 9\times10^{9}Nm^{2}/c^{2}
Q คือ ปริมาณประจุไฟฟ้าที่เป็นต้นกำเนิด (Point Charge) หน่วย คูลอมบ์ (C)
R คือ ระยะห่างจากประจุถึงจุดที่พิจารณา หน่วย เมตร (m)
**คำนวณโดยแทนค่า +/- ของ Q
แนวในการหาศักย์ไฟฟ้าจากจุดประจุ
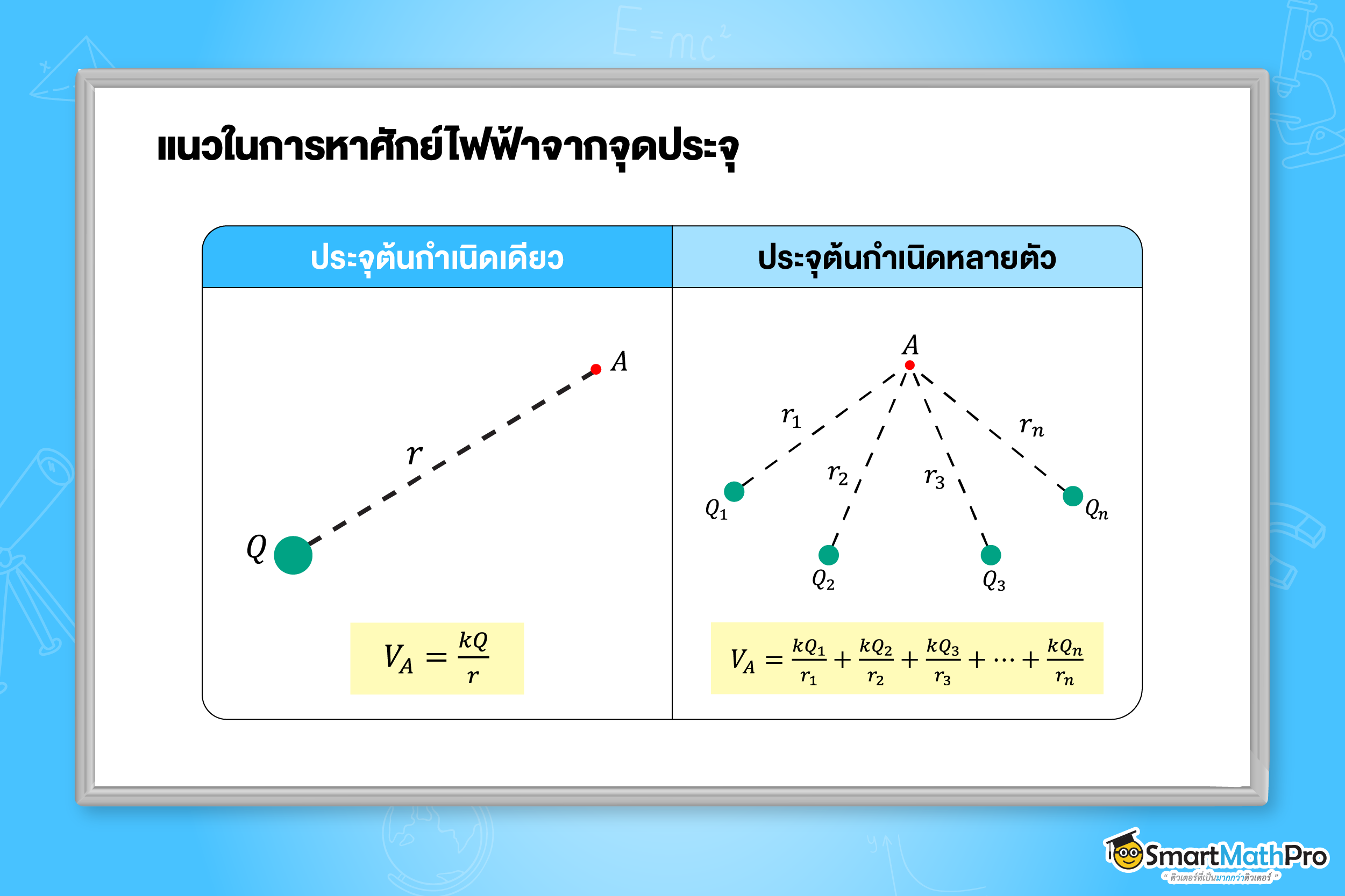
**คำนวณโดยแทนค่า +/- ของ Q
ศักย์ไฟฟ้าในตัวนำทรงกลม
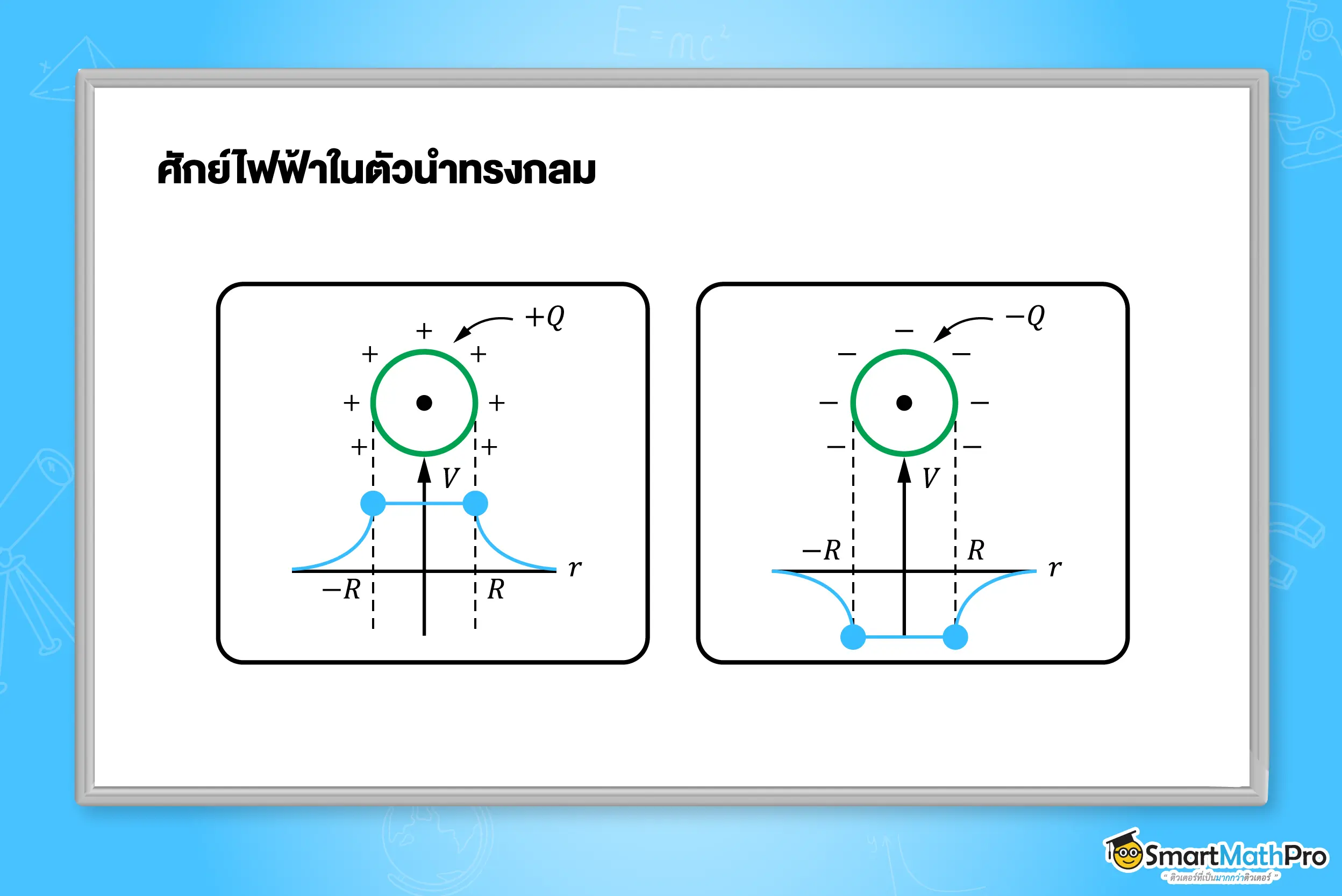
การเปลี่ยนแปลงของศักย์ไฟฟ้า (V) เทียบกับระยะทาง (r) จากจุดศูนย์กลาง
เมื่อ r< R (ภายใน) : V มีค่า คงที่ และเท่ากับ V พื้นผิว (V=\frac{kQ}{R})
เมื่อ r= R (ที่พื้นผิว) : V มีค่า สูงสุด (สำหรับประจุบวก) หรือต่ำสุด (สำหรับประจุลบ) (V=\frac{kQ}{R})
เมื่อ r> R (ภายนอก) : V จะ ลดลง เมื่อระยะ r เพิ่มขึ้น (มีค่าแปรผกผันกับ r) (V=\frac{kQ}{r})
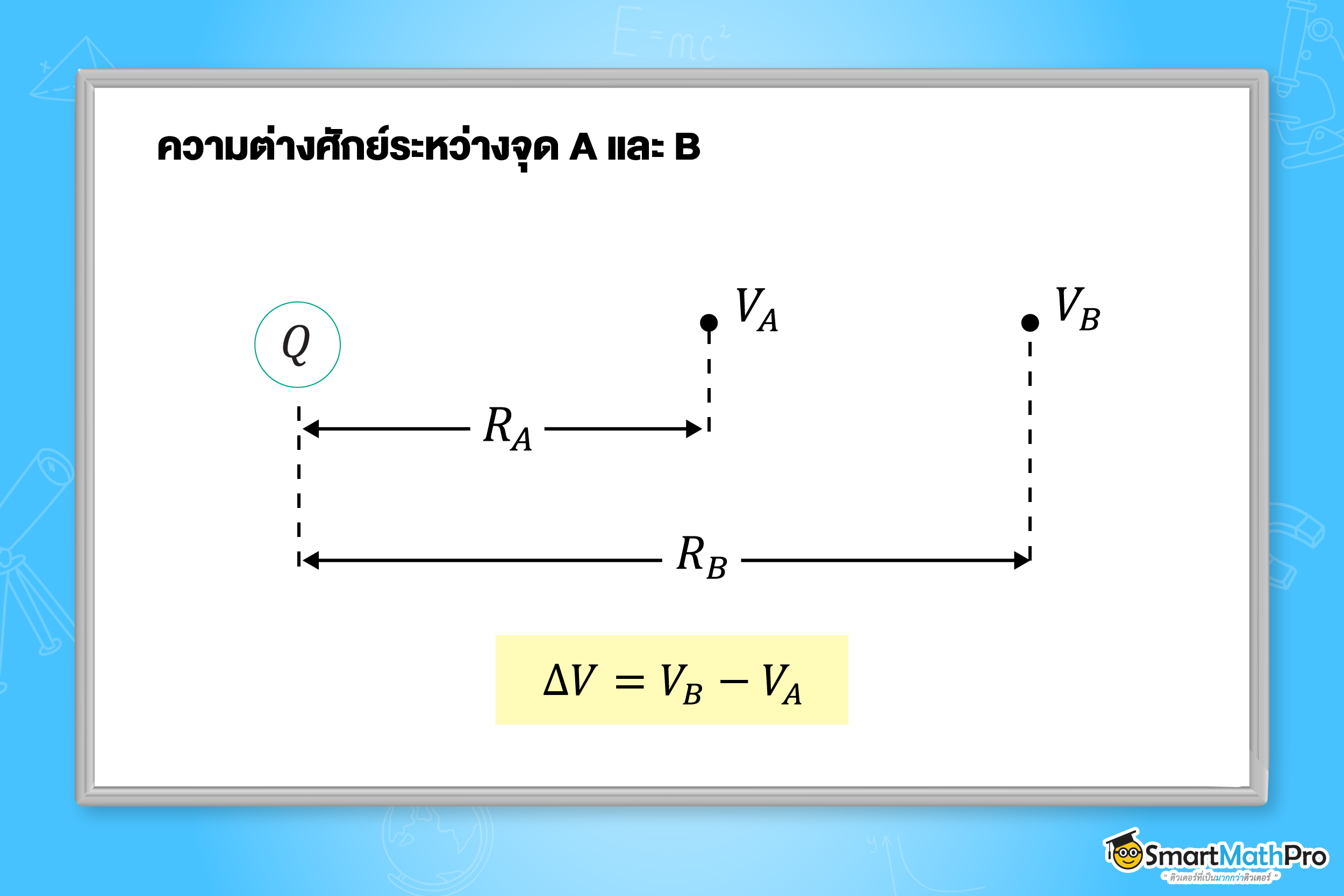
ความต่างศักย์
ความต่างศักย์ หรือที่นิยมเรียกว่า แรงดันไฟฟ้า (Voltage) คือ ผลต่างของศักย์ไฟฟ้าระหว่างสองจุดใด ๆ
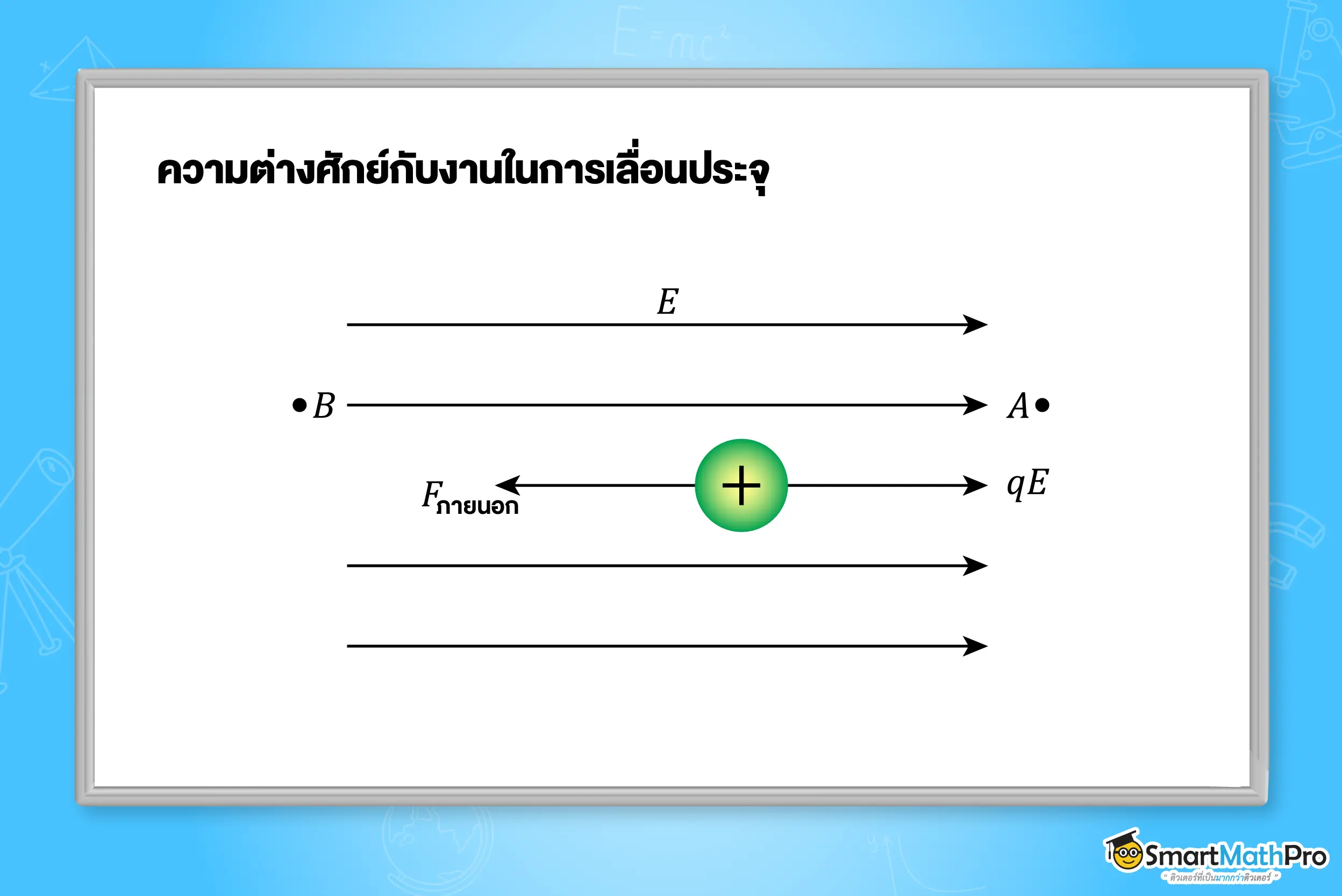
งานในการเลื่อนประจุและพลังงานศักย์ไฟฟ้า
หากมีแรงภายนอกย้ายประจุจากจุด A ไป ยังจุด B จะได้งานในการย้ายประจุ ได้ดังนี้
W_{A\to B}=q(V_{B}-V_{A})
W_{A\to B}=q(\Delta V)
กรณีที่ลากจากระยะไกลมาก ๆ (\infty) มาที่จุดใด ๆ
W_{A\to B}=q(V_{B}-V_{A})
W_{\infty \to point}=q(V_{point}-V_{\infty })
จะได้ว่า
งานที่ทำโดยแรงภายนอกในการเลื่อนประจุจากระยะอนันต์มายังตำแหน่งที่พิจารณาภายในสนามไฟฟ้า
คือ พลังงานศักย์ไฟฟ้าในระบบ จะได้ว่า
U=qV
ดังนั้น พลังงานศักย์ไฟฟ้า มีค่าดังนี้
U=\frac{kqQ}{r}
โดยที่
U คือ พลังงานศักย์ไฟฟ้า (Electric Potential Energy) หน่วย จูล (J)
k คือ ค่าคงที่ของคูลอมบ์ (Coulomb’s Constant) ค่าประมาณ 9\times 10^{9}Nm^{2}/c^{2}
q,Q คือ ปริมาณประจุไฟฟ้า (Charge) หน่วย คูลอมบ์ (C)
r คือ ระยะห่างระหว่างประจุ (Distance) หน่วย เมตร (m)
**คำนวณโดยแทนค่า +/- ของ Q และ q
ความต่างศักย์เนื่องจากสนามไฟฟ้าสม่ำเสมอ
เมื่อต่อความต่างศักย์ (\Delta V)เข้ากับแผ่นโลหะคู่ขนาน จะเกิดสนามไฟฟ้าสม่ำเสมอ โดยความต่างศักย์ไฟฟ้าระหว่างสองตำแหน่งใด ๆ ในสนามไฟฟ้าสม่ำเสมอ จะได้ความสัมพันธ์ตามสมการ ดังนี้
จงคำนวณหาศักย์ไฟฟ้า ณ จุดหนึ่งที่อยู่ห่างจากประจุไฟฟ้า Q=+5\times 10^{-6}คูลอมบ์ เป็นระยะR=0.5 เมตร
วิธีทำ
จากสูตรศักย์ไฟฟ้าจากจุดประจุ V=\frac{kQ}{R}
จะได้ว่า V=\frac{(9\times 10^{9})(5\times 10^{-6})}{0.5}
V=\frac{45\times 10^{3}}{0.5}
V=90\times 10^{3}
V=90,000V
ตอบ ศักย์ไฟฟ้า ณ จุดนั้นมีค่าเท่ากับ 90,000 โวลต์
ความจุไฟฟ้า (Capacitance)
ความจุไฟฟ้า(Capacitance) คือ ความสามารถของตัวนำไฟฟ้าในการสะสมประจุไฟฟ้า เมื่อมีศักย์ไฟฟ้า (Voltage) คร่อมตัวนำนั้น ยิ่งตัวนำมีความจุไฟฟ้ามากเท่าไหร่ ก็จะสามารถสะสมประจุไฟฟ้าได้มากขึ้นภายใต้แรงดันไฟฟ้าเดียวกัน
C=\frac{Q}{\Delta V}
โดยที่
C คือ ความจุไฟฟ้า (Capacitance) มีหน่วยเป็น ฟารัด (F)
Q คือ ปริมาณประจุไฟฟ้า (Charge) ที่สะสม มีหน่วยเป็น คูลอมบ์(C)
\Delta V คือ ความต่างศักย์ (Voltage) ที่คร่อมตัวนำ มีหน่วยเป็น โวลต์ (V)
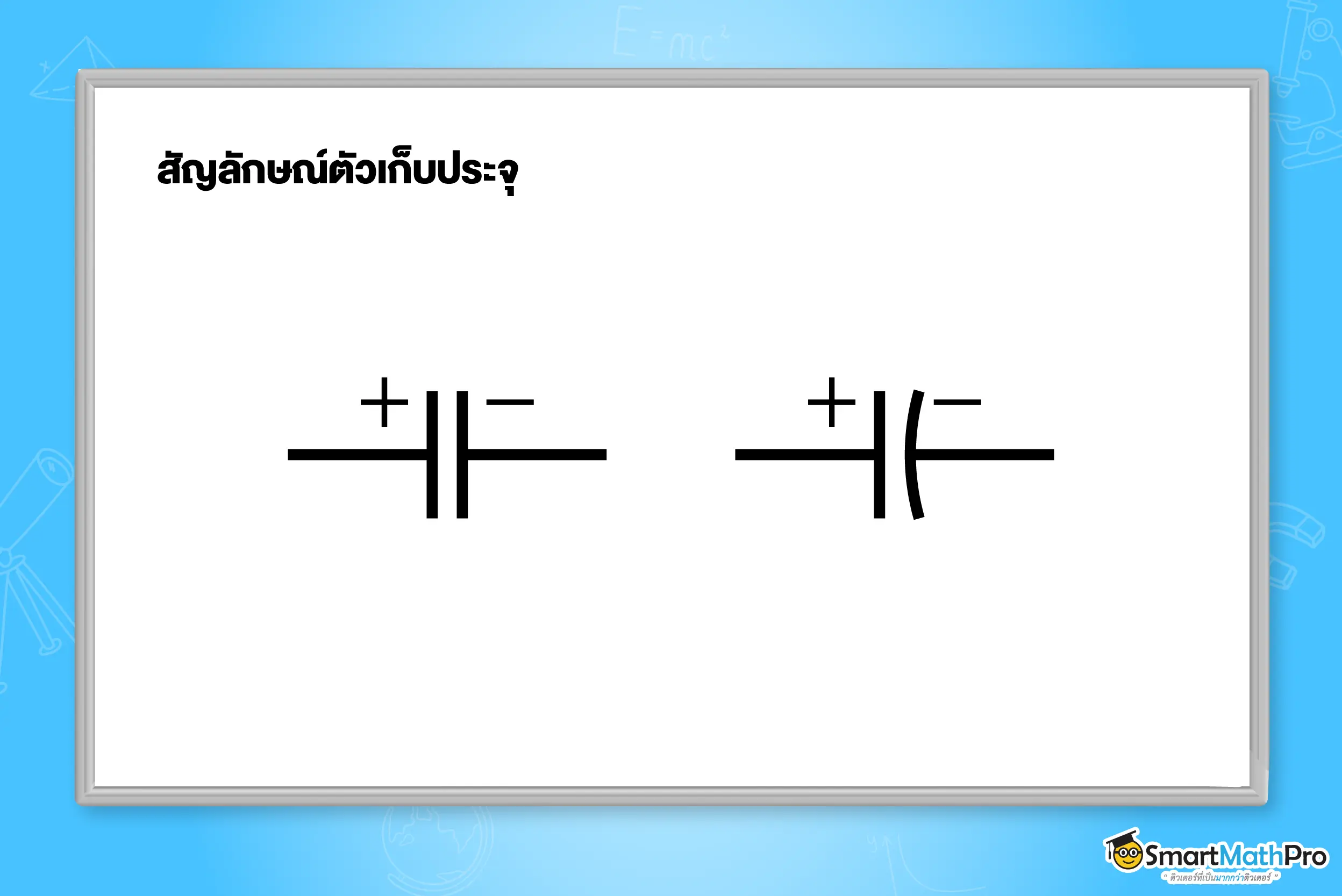
ตัวเก็บประจุ
ตัวเก็บประจุโดยทั่วไปประกอบด้วย ตัวนำไฟฟ้าสองแผ่น (Plates) วางขนานกัน และมี วัสดุฉนวน (Dielectric) คั่นกลาง เมื่อมีแรงดันไฟฟ้า (Voltage) คร่อมตัวนำทั้งสองแผ่น จะเกิดการสะสมประจุไฟฟ้าบนแต่ละแผ่นโดยแผ่นหนึ่งจะมี
ประจุบวก และอีกแผ่นหนึ่งจะมีประจุลบในปริมาณที่เท่ากัน สนามไฟฟ้าจะถูกสร้างขึ้นระหว่างแผ่นตัวนำทั้งสอง โดยมีทิศทางจากแผ่นที่มีประจุบวกไปยังแผ่นที่มีประจุลบ
การต่อตัวเก็บประจุ
การต่อตัวเก็บประจุ เป็นการนำตัวเก็บประจุหลายตัวมาเชื่อมต่อกันในวงจรไฟฟ้า เพื่อให้ได้ค่าความจุรวม (Equivalent Capacitance) ที่ต้องการ ซึ่งอาจมีค่ามากกว่า น้อยกว่า หรือเท่ากับค่าความจุของตัวเก็บประจุแต่ละตัว
การต่อตัวเก็บประจุหลัก ๆ มี 2 แบบ คือ
พลังงานสะสมในตัวเก็บประจุ
พลังงานสะสมในตัวเก็บประจุ คือ พลังงานไฟฟ้าที่ถูกสะสมไว้ในตัวเก็บประจุในรูปของสนามไฟฟ้า เมื่อมีการชาร์จประจุไฟฟ้าเข้าไปในตัวเก็บประจุ
U=\frac{1}{2}C\Delta V^{2}=\frac{1}{2}Q\Delta V=\frac{Q}{2C^{2}}
โดยที่
U คือ พลังงานที่สะสมในตัวเก็บประจุ (Energy stored in capacitor) หน่วย จูล (J)
C คือ ความจุไฟฟ้า (Capacitance) หน่วย ฟารัด (F)
Q คือ ปริมาณประจุไฟฟ้า (Charge) ที่สะสมในตัวเก็บประจุ หน่วย คูลอมบ์ (C)
\Delta V คือ ความต่างศักย์ (Voltage) ที่คร่อมตัวเก็บประจุ หน่วย โวลต์ (V)
ข้อที่ 1
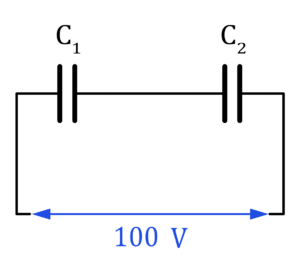
จากรูป C_{1}=5\mu F และ C_{2}=15\mu F
ต่ออนุกรมเข้ากับความต่างศักย์100 V ดังรูป
จงหาความต่างศักย์ระหว่างขั้วC_{1} และ C_{2}
วิธีทำ
หาความจุรวม
\frac{1}{C_{total}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}
\frac{1}{C_{total}}=\frac{1}{5}+\frac{1}{15}=\frac{4}{15}
\frac{1}{C_{total}}=\frac{15}{4}=3.75\mu F
หาประจุรวม
Q_{total}=C_{total}\Delta V_{total}
Q_{total}=(3.75\times 10^{-6})(100)
Q_{total}=375\mu C
หาความต่างศักย์แต่ละตัว (Q แต่ละตัวเท่ากัน)
V_{1}=\frac{Q_{total}}{C_{1}}=\frac{375\times 10^{6}}{5\times 10^{6}}=75V
V_{2}=\frac{Q_{total}}{C_{2}}=\frac{375\times 10^{6}}{15\times 10^{6}}=25V
ตอบ V_{1}=75V,V_{2}=25V
โจทย์เกี่ยวกับไฟฟ้าสถิตพร้อมเฉลย
ตอบ 3. ประจุลบขนาด 1 ไมโครคูลอมบ์
วิธีทำ
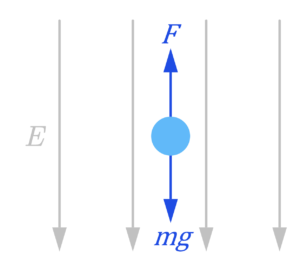
\Sigma F=0
F_{\uparrow }=F_{\downarrow }
qE = mg
q(600)=0.006\times 10^{-3}
q=1\times 10^{-6}C
วัตถุจะสามารถลอยนิ่งในสนามไฟฟ้าได้ เนื่องจากแรงทางไฟฟ้าต้องมีทิศชี้ขึ้นซึ่งตรงข้ามกับสนามไฟฟ้า จึงเป็นประจุลบ
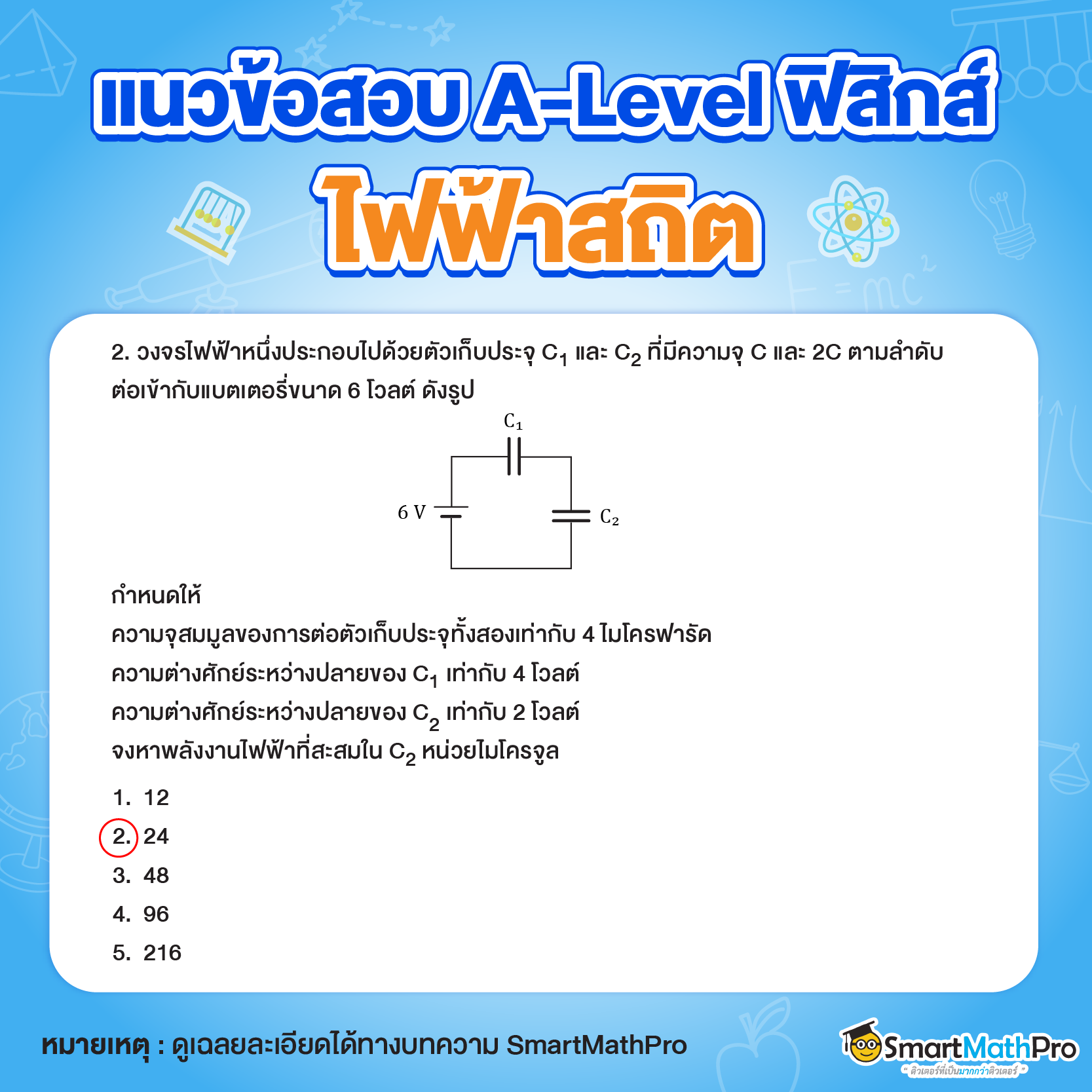
ตอบ ข้อ 2. 24
วิธีทำ
หาค่า C_{1} และ C_{2} จากโจทย์ ตัวเก็บประจุต่ออนุกรม
\frac{1}{C_{total}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}
\frac{1}{4\mu F}=\frac{1}{C}+\frac{1}{2C}
2C=12\mu F
C=6\mu F
ดังนั้น เราจะได้ค่าความจุแต่ละตัว
C_{1}=6\mu F
C_{2}=12\mu F
คำนวณหาค่าพลังงานไฟฟ้าที่สะสมใน C_{2}
U=\frac{1}{2}CV^{2}
U=\frac{1}{2}(12\times 10^{-6})(2)^{2}
U=24\times 10^{-6}J=24\mu J
เก็บเนื้อหาไฟฟ้าสถิตให้แม่นกับ SmartMathPro
สำหรับใครที่เก็บเนื้อหานี้เพื่อเตรียมสอบ A-Level ฟิสิกส์ และยังมีเนื้อหาบางจุดที่ไม่เข้าใจ อยากมีตัวช่วยเพื่อให้เก็บเนื้อหาได้เข้าใจมากขึ้น
พี่ขอแนะนำคอร์สเรียนพิเศษสนาม A-Level ของ SmartMathPro ที่มีทั้ง A-Level คณิต 1, 2 / A-Level ภาษาอังกฤษ / A-Level ฟิสิกส์ / A-Level ภาษาไทย / A-Level สังคม เลยน้าา โดยสำหรับใครที่ไม่มีพื้นฐานก็สามารถเรียนได้ เพราะพี่สอนตั้งแต่ปูพื้นฐาน ไปจนถึงพาทำโจทย์ตั้งแต่ระดับง่ายไปจนถึงความยากใกล้เคียงกับข้อสอบจริงเลย แถมมีเทคนิคในการทำข้อสอบอีกเพียบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้น > <
และสำหรับใครที่ยังไม่เริ่ม เริ่มติวตอนนี้ก็ยังทันน้าา แอบกระซิบว่าถ้าสมัครคอร์สตั้งแต่ตอนนี้พี่มี Unseen Mock Test ชุดพิเศษ 1 ชุด แถมฟรีไปให้ลองทำพร้อมสิทธิพิเศษประจำเดือนอีกมากมายด้วย ถ้าน้อง ๆ คนไหนสนใจคอร์สเตรียมสอบ A-Level สามารถ คลิก เข้ามาดูรายละเอียดได้เลยย
เป็นอย่างไรกันบ้างกับ “สรุปเนื้อหาเรื่อง ไฟฟ้าสถิต ฟิสิกส์ ม.5” และแนวข้อสอบที่พี่นำมาฝากในวันนี้ แนะนำว่าถ้าใครอยากจะแม่นเนื้อหาเรื่องนี้ นอกจากก็อ่านเนื้อหาแล้ว ก็ควรทบทวนอย่างเป็นประจำและฝึกทำแบบฝึกหัดเยอะ ๆ เพื่อให้เข้าใจมากขึ้นด้วยน้าา
บทความ แนะนำ
A-Level ฟิสิกส์ 68 สอบอะไรบ้าง ? มีกี่ข้อ ? พร้อมตัวอย่างข้อสอบ
A-Level 68 คืออะไร? มีกี่ข้อ? มีวิชาอะไรบ้าง? สรุปพร้อมคลิปติว
เสียง ฟิสิกส์ ม.5 สรุปเนื้อหา พร้อมสูตรและตัวอย่างโจทย์
สรุป แสงเชิงคลื่น ฟิสิกส์ ม.5 พร้อมโจทย์และเฉลย
บทความ แนะนำ
A-Level ฟิสิกส์ 68 สอบอะไรบ้าง ? มีกี่ข้อ ? พร้อมตัวอย่างข้อสอบ
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
