สรุป การเคลื่อนที่แนวตรง ฟิสิกส์ ม.4 พร้อมโจทย์และเฉลย

เนื้อหาเรื่อง การเคลื่อนที่แนวตรง ฟิสิกส์ เป็นบทใหญ่อีกบทหนึ่งที่น้อง ๆ หลายคนยังไม่ค่อยเข้าใจในเนื้อหา
แต่ไม่ต้องกังวลไปน้า

เพราะพี่เตรียมสรุปเรื่องการเคลื่อนที่แนวตรงมาให้ครบ ไม่ว่าจะเป็นเรื่องนิยาม ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แนวตรง สูตรเกี่ยวกับการเคลื่อนที่แนวตรง และเนื้อหาที่สำคัญอื่น ๆ พร้อมตัวอย่างข้อสอบท้ายบทความและแบบฝึกหัดเพิ่มเติมให้ทุกคนอีกด้วยย

สนใจหัวข้อไหน ... กดอ่านเลย

การเคลื่อนที่แนวตรงคืออะไร ?

การเคลื่อนที่แนวตรง (linear motion) หรือการเคลื่อนที่ในหนึ่งมิติ คือ การเปลี่ยนตำแหน่งของวัตถุไปตามแนวเส้นตรง เช่น รถไฟวิ่งบนรางตรง การตกของก้อนหิน หรือการกลิ้งของลูกบอลตามพื้นเอียง

ในการอธิบายการเคลื่อนที่ของวัตถุใด ๆ เราจำเป็นต้องระบุ ตำแหน่ง (position) โดยการบอกจุดที่วัตถุอยู่ ณ เวลาใดเวลาหนึ่งเมื่อเทียบกับจุดอ้างอิงที่เรากำหนด เช่น รถคันนี้อยู่ห่างจากเสาไฟฟ้าไปทางทิศตะวันออก $50$ เมตร จากตัวอย่างข้างต้นมี เสาไฟฟ้า เป็นจุดอ้างอิง

ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แนวตรง

ปริมาณในทางฟิสิกส์จะแบ่งออกเป็น 2 ประเภท คือ

ปริมาณสเกลาร์ (Scalar) เป็นปริมาณที่บอกแค่ ขนาด โดยไม่ต้องระบุทิศทาง เช่น $10$ วินาที
ปริมาณเวกเตอร์ (Vector) เป็นปริมาณที่บอกทั้ง ขนาดและทิศทาง เช่น $5$ เมตรไปทางทิศเหนือ

สำหรับการเคลื่อนที่แนวตรง จำเป็นต้องรู้จักกับปริมาณที่เกี่ยวข้องกับการเคลื่อนที่ เพื่อให้สามารถอธิบายการเคลื่อนที่แนวตรงของวัตถุได้ ดังนี้

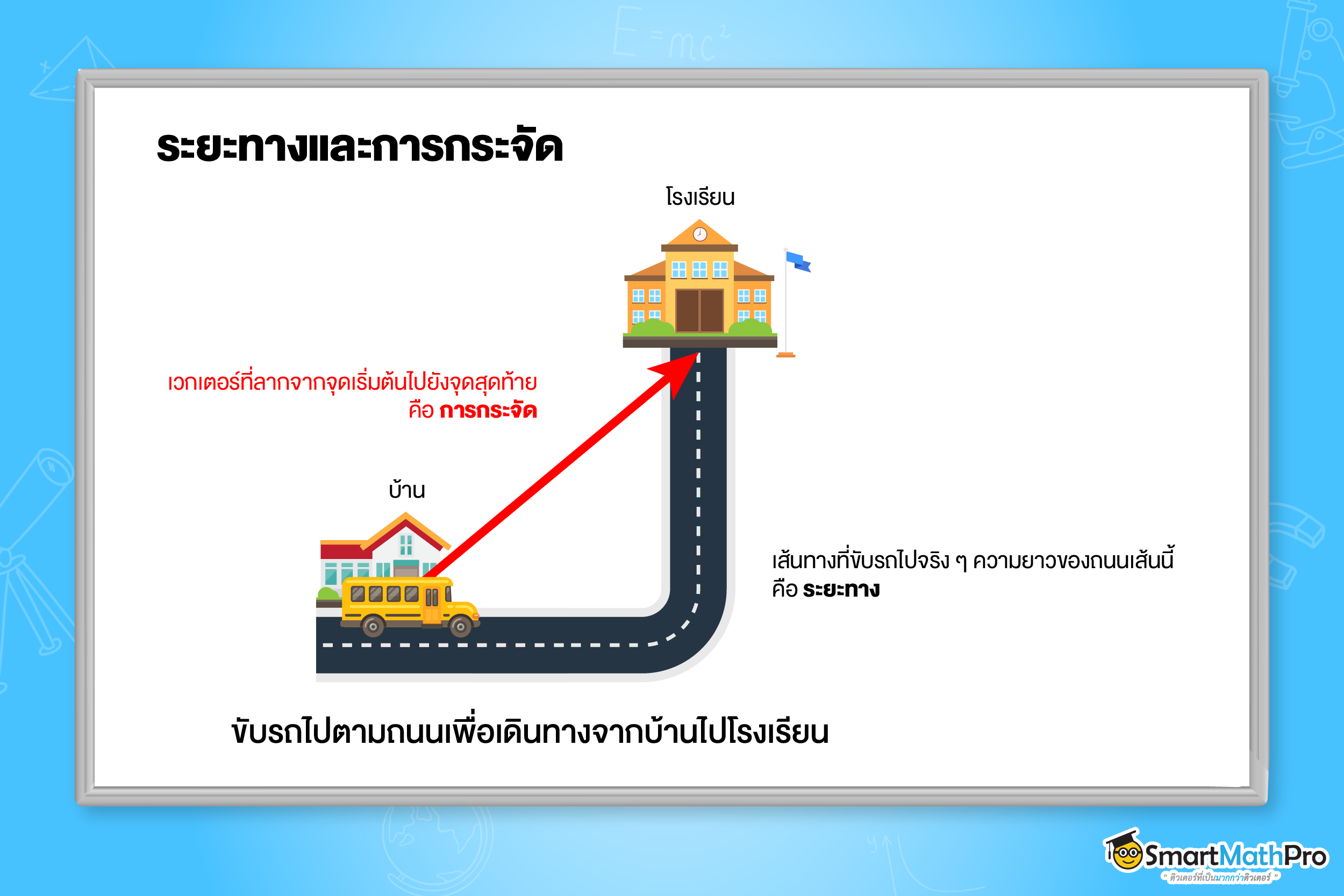
ระยะทางและการกระจัด

ระยะทาง (Distance) คือ ความยาวทั้งหมดของเส้นทางการเคลื่อนที่ของวัตถุเป็นปริมาณสเกลาร์
การกระจัด (Displacement) คือ เวกเตอร์ที่ลากจากจุดเริ่มต้นไปยังจุดสุดท้ายของการเคลื่อนที่เป็นเส้นตรง

ตัวอย่างโจทย์ : การกระจัดและระยะทาง

1. โยนก้อนหินขึ้นในแนวดิ่งจากดาดฟ้าตึกสูง $20$ เมตร ก้อนหินขึ้นไปได้สูงสุดจากดาดฟ้าเป็นระยะ $10$ เมตร แล้วตกถึงพื้นดินระยะทางและการกระจัดในการโยนก้อนหินมีค่าเท่าใด

วิธีทำ
เมื่อเริ่มโยนก้อนหินขึ้นในแนวดิ่ง ก้อนหินจะเคลื่อนที่ดังนี้

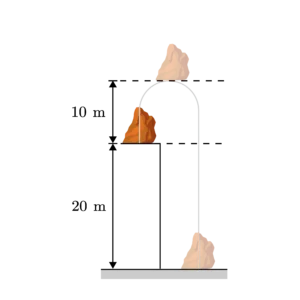
ช่วงที่ 1 ก้อนหินเคลื่อนที่ขึ้นไปจากดาดฟ้าได้สูงสุด $10$ เมตร
ช่วงที่ 2 ก้อนหินตกลงมาจากจุดสูงสุดจนถึงดาดฟ้าเป็นระยะ $10$ เมตร
ช่วงที่ 3 ก้อนหินตกลงมาจากดาดฟ้าถึงพื้นดินเป็นระยะ $20$ เมตร
นำระยะทางที่ก้อนหินเคลื่อนที่แต่ละช่วงมารวมกัน
ระยะทาง $= 10 + 10 + 20 = 40\text{ m}$

เนื่องจากก้อนหินเคลื่อนที่จากดาดฟ้าซึ่งเป็นจุดเริ่มต้น และจุดสุดท้ายไปอยู่ที่พื้นดิน ดังนั้น
การกระจัด จึงเท่ากับความสูงของตึก
การกระจัด $20\text{ m}$ (ในทิศทางลง)

ตอบ ระยะทางและการกระจัดในการโยนก้อนเท่ากับ $40$ และ $20$ เมตร (ในทิศทางลง) ตามลำดับ

อัตราเร็วและความเร็ว

อัตราเร็ว (Speed) คือ ระยะทางทั้งหมดที่เคลื่อนที่ได้ในหนึ่งหน่วยเวลา เป็นปริมาณสเกลาร์
ความเร็ว (Velocity) คือ การกระจัดในหนึ่งหน่วยเวลา เป็นปริมาณเวกเตอร์

ตัวอย่างโจทย์ : อัตราเร็ว และความเร็ว

พี่ฟาร์มวิ่งออกกำลังกายโดยเริ่มวิ่งจากบ้านไปทางทิศตะวันออก $30$ เมตรหลังจากนั้นวิ่งไปทางทิศเหนืออีก $40$ เมตรจนสิ้นสุดการวิ่งที่สวนหน้าหมู่บ้าน อยากทราบว่าพี่ฟาร์มวิ่งด้วยอัตราเร็ว และความเร็วเท่าไร หากพี่ฟาร์มใช้เวลาในการวิ่งทั้งหมด $5$ นาที

วิธีทำ
วาดแผนภาพการวิ่งของพี่ฟาร์มได้ดังรูป

นำระยะทางที่พี่ฟาร์มวิ่งแต่ละช่วงมารวมกัน
ระยะทาง $30+40=70\text{ m}$

หาอัตราเร็วของพี่ฟาร์ม

$v=\frac{s}{\bigtriangleup t} \\ v=\frac{70}{5\times 60} \\ v=\frac{70}{300} \\ v=0.23 \text{ m/s}$

การกระจัดที่พี่ฟาร์มวิ่งหาได้จากเวกเตอร์ที่ชี้
จากจุดเริ่มต้น (บ้าน) ไปหาจุดสุดท้าย (สุดท้าย) ดังรูป

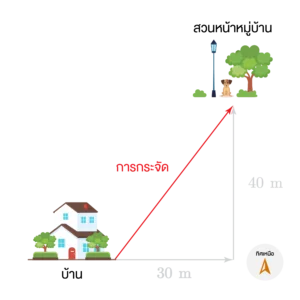
โดยขนาดของการกระจัดจากทฤษฎีบทพีทาโกรัส
ขนาดการกระจัด $=\sqrt{30^{2}+40^{2}}$
ขนาดการกระจัด $=\sqrt{900+1600}$
ขนาดการกระจัด $=50\text{ m}$

หาความเร็วของพี่ฟาร์ม
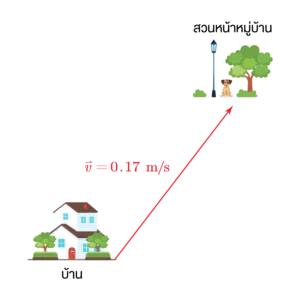
$\overset{\rightharpoonup}{v}=\frac{\overset{\rightharpoonup}{s}}{\bigtriangleup t} \\ \overset{\rightharpoonup}{v}=\frac{50}{5\times 60} \\ \overset{\rightharpoonup}{v}=\frac{50}{300} \\ \overset{\rightharpoonup}{v}=0.17 \text{ m/s}$
ตอบ พี่ฟาร์มวิ่งด้วยอัตราเร็วเท่ากับ $0.23$ เมตรต่อวินาที
และความเร็วเท่ากับ $0.17$ เมตรต่อวินาที ทิศทางดังรูป

ความเร่ง (Acceleration)

คือ ความเร็วที่เปลี่ยนแปลงไปของวัตถุเมื่อเวลาผ่านไป ไม่ว่าจะเป็นการเพิ่มขึ้นหรือลดลงของความเร็ว หรือการเปลี่ยนทิศทางของการเคลื่อนที่ เป็นปริมาณเวกเตอร์

ตัวอย่างโจทย์ : ความเร่ง

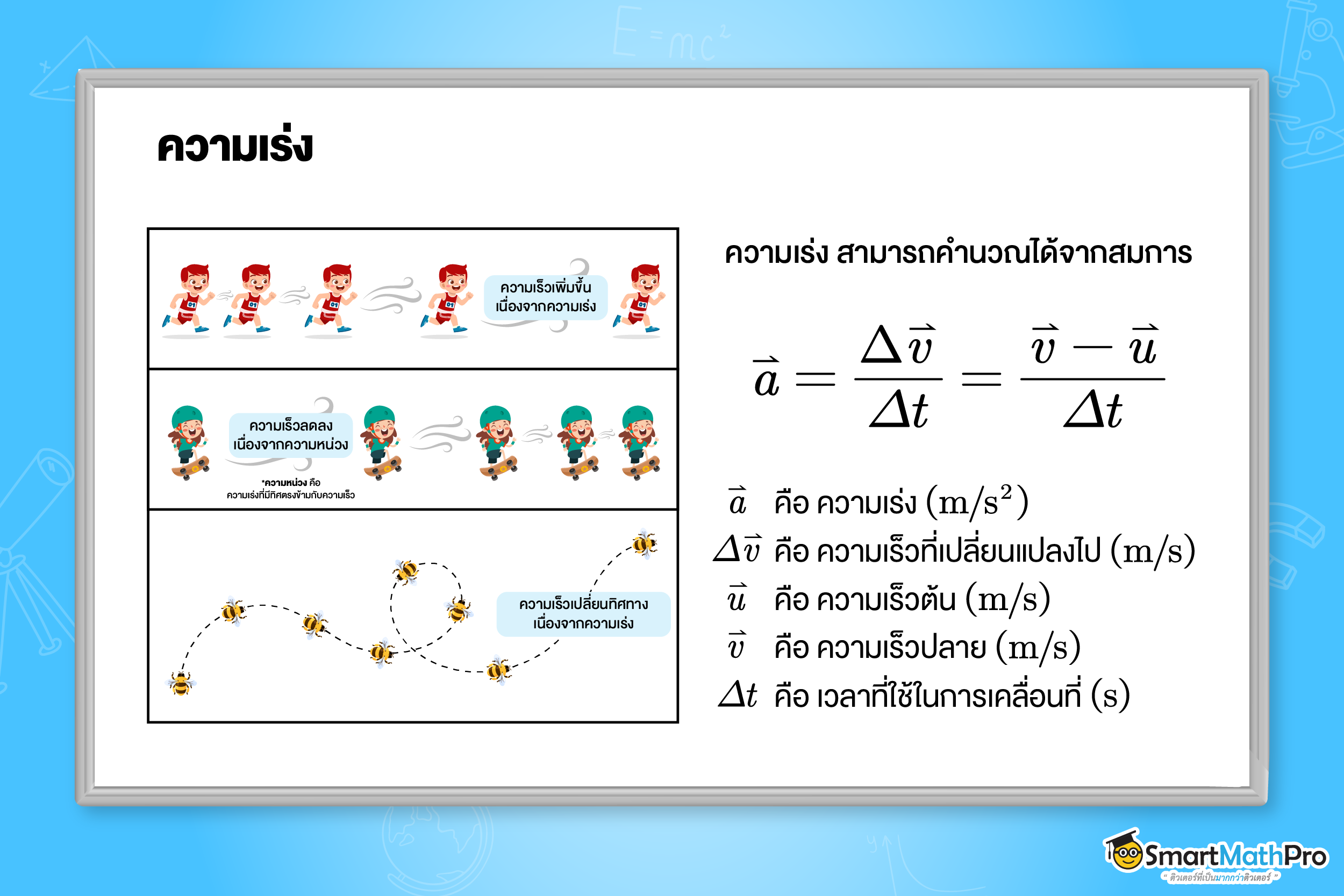
รถเริ่มเคลื่อนที่แนวตรง และมีความเร็วเป็น $20$ เมตรต่อวินาที ในเวลา $5$ วินาที จงหาขนาดความเร่งของรถ

วิธีทำ
รถเริ่มเคลื่อนที่ หมายความว่า ความเร็วต้นในการเคลื่อนที่เท่ากับ $0$ เมตรต่อวินาที
หาความเร่งของรถ
$\overset{\rightharpoonup}{a}=\frac{\overset{\rightharpoonup}{v}-\overset{\rightharpoonup}{u}}{\bigtriangleup t} \\ \overset{\rightharpoonup}{a}=\frac{20-0}{5} \\ \overset{\rightharpoonup}{a}=4 \text{ m/s}^{2}$

ตอบ รถเคลื่อนที่ด้วยความเร่ง $4$ เมตรต่อวินาทียกกำลังสอง

สูตรเกี่ยวกับการเคลื่อนที่แนวตรง

สมการการเคลื่อนที่ของวัตถุในแนวตรงกรณีความเร่งมีค่าคงตัวได้ดังนี้

ตัวอย่างโจทย์ : การเคลื่อนที่แนวตรง

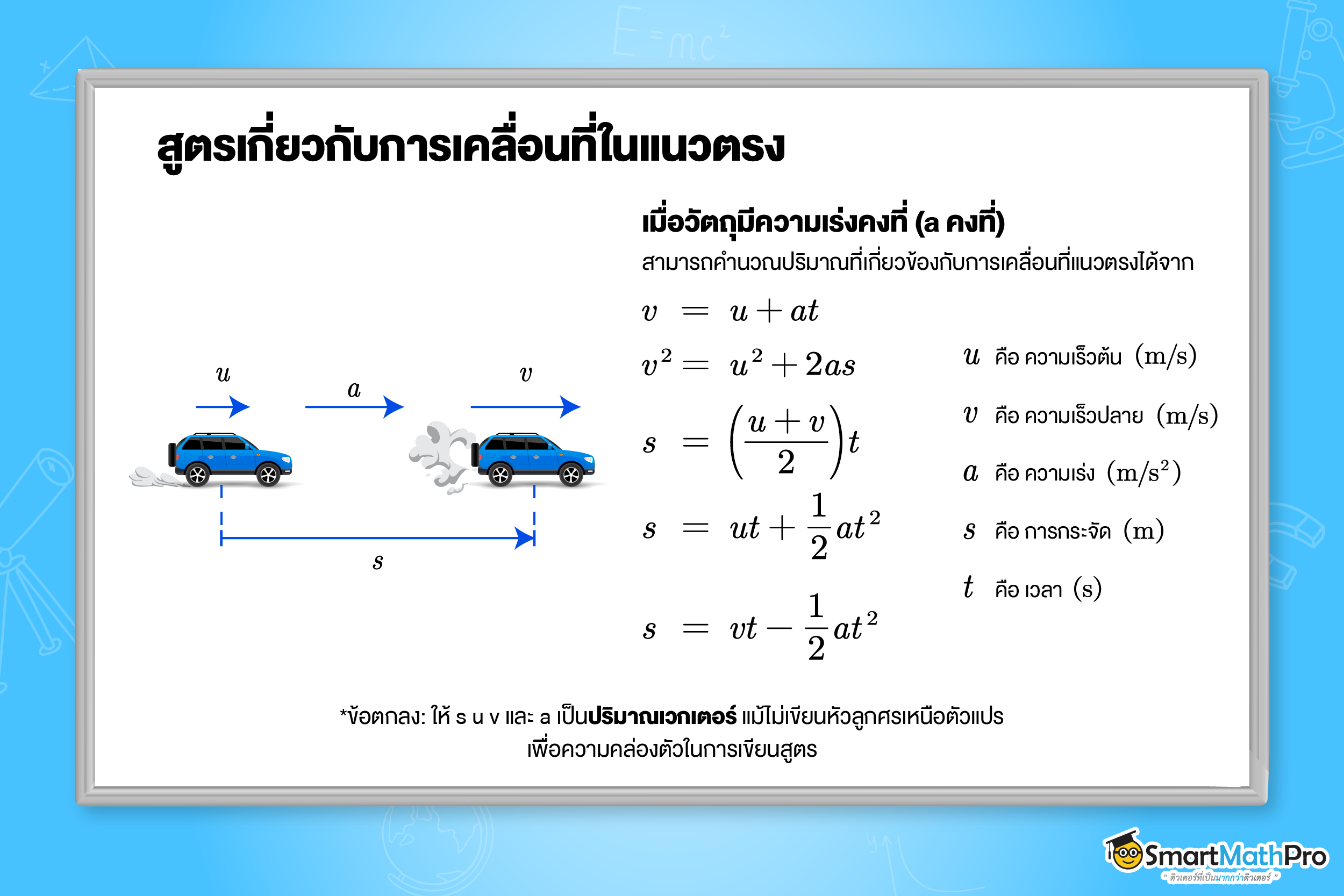
1. วัตถุหนึ่งเคลื่อนที่ในแนวเส้นตรงด้วยความเร่งคงตัว $4$ เมตรต่อวินาทียกกำลังสอง โดยมีความเร็วต้น $2$ เมตรต่อวินาที ในทิศทางเดียวกับความเร่ง จงหาความเร็วของวัตถุ เมื่อเวลาผ่านไป $10$ วินาที

วิธีทำ
หาความเร็วของวัตถุ
$v=u+at \\ v=2+4(10) \\ v=42 \text{ m/s}$

ตอบ วัตถุเคลื่อนที่ด้วยความเร็ว $42$ เมตรต่อวินาที

2. วัตถุหนึ่งเคลื่อนที่ในแนวตรงด้วยความเร่งคงตัว โดยมีความเร็วต้น 4.0 เมตรต่อวินาที เมื่อเคลื่อนที่ไปได้ 5 วินาที วัตถุมีความเร็วเป็น 2.0 เมตรต่อวินาที ในทิศตรงกันข้ามกับความเร็วต้น วัตถุนี้มีการกระจัดเท่าใด

วิธีทำ
กำหนดให้ ทิศทางเดียวกับความเร็วต้นเป็นบวก และทิศตรงกันข้ามกับความเร็วต้นเป็นลบ
หาการกระจัดของวัตถุ

$s=\left(\frac{u+v}{2}\right)t \\ s=\left(\frac{4+(-2)}{2}\right)5 \\ s=\left(\frac{2}{2}\right)5 \\ s=5 \text{ m}$

ตอบ วัตถุมีการกระจัดเป็น $5$ เมตร ทิศทางเดียวกับความเร็วต้น $+$

3. ขับรถด้วยความเร็ว $20$ เมตรต่อวินาที ห้ามล้อให้รถหยุด (เหยียบเบรก) ด้วยความหน่วง $2$ เมตรต่อวินาทียกกำลังสอง จงหาระยะทางที่ใช้เพื่อหยุดรถนับตั้งแต่ที่เริ่มห้ามล้อ

วิธีทำ
ความหน่วง คือ ความเร่งที่มีทิศทางตรงกันข้ามกับการเคลื่อนที่
กำหนดให้ ทิศทางเดียวกับการเคลื่อนที่เป็นบวก และทิศตรงกันข้ามกับการเคลื่อนที่เป็นลบ
กำหนดให้

$v^{2}=u^{2}+2as \\ 0=20^{2}+2(-2)s \\ 0=400-4s \\ 4s=400 \\ s=100\text{ m}$

ตอบ ระยะทางที่ใช้เพื่อหยุดรถนับตั้งแต่ที่เริ่มห้ามล้อเท่ากับ $100$ เมตร

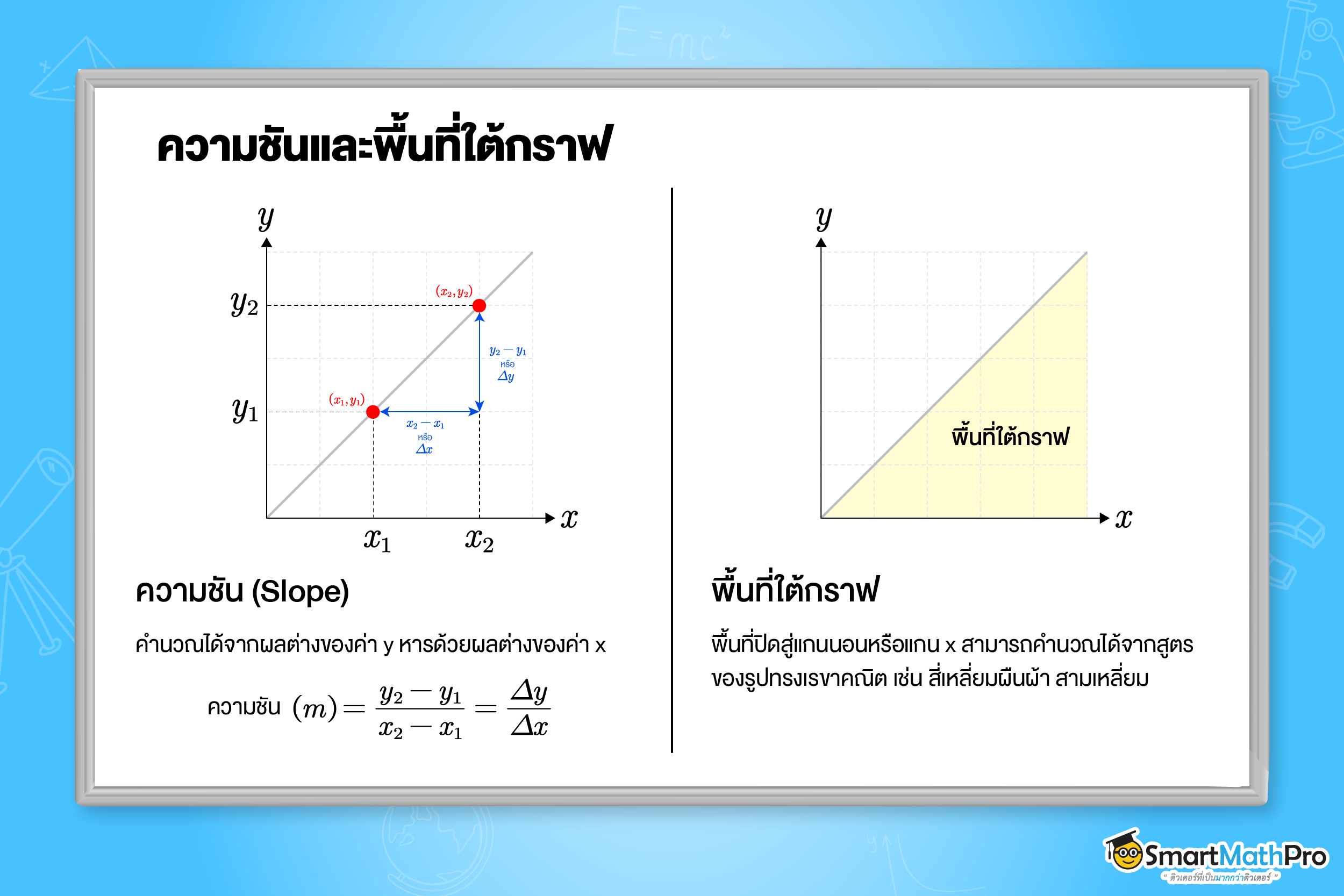
กราฟของการเคลื่อนที่แนวตรง

การวิเคราะห์ ความชัน และพื้นที่ใต้กราฟ เป็นสองวิธีหลักในการทำความเข้าใจการเคลื่อนที่ของวัตถุจากกราฟ ซึ่งสามารถหาความชันและพื้นที่ใต้กราฟได้ดังนี้

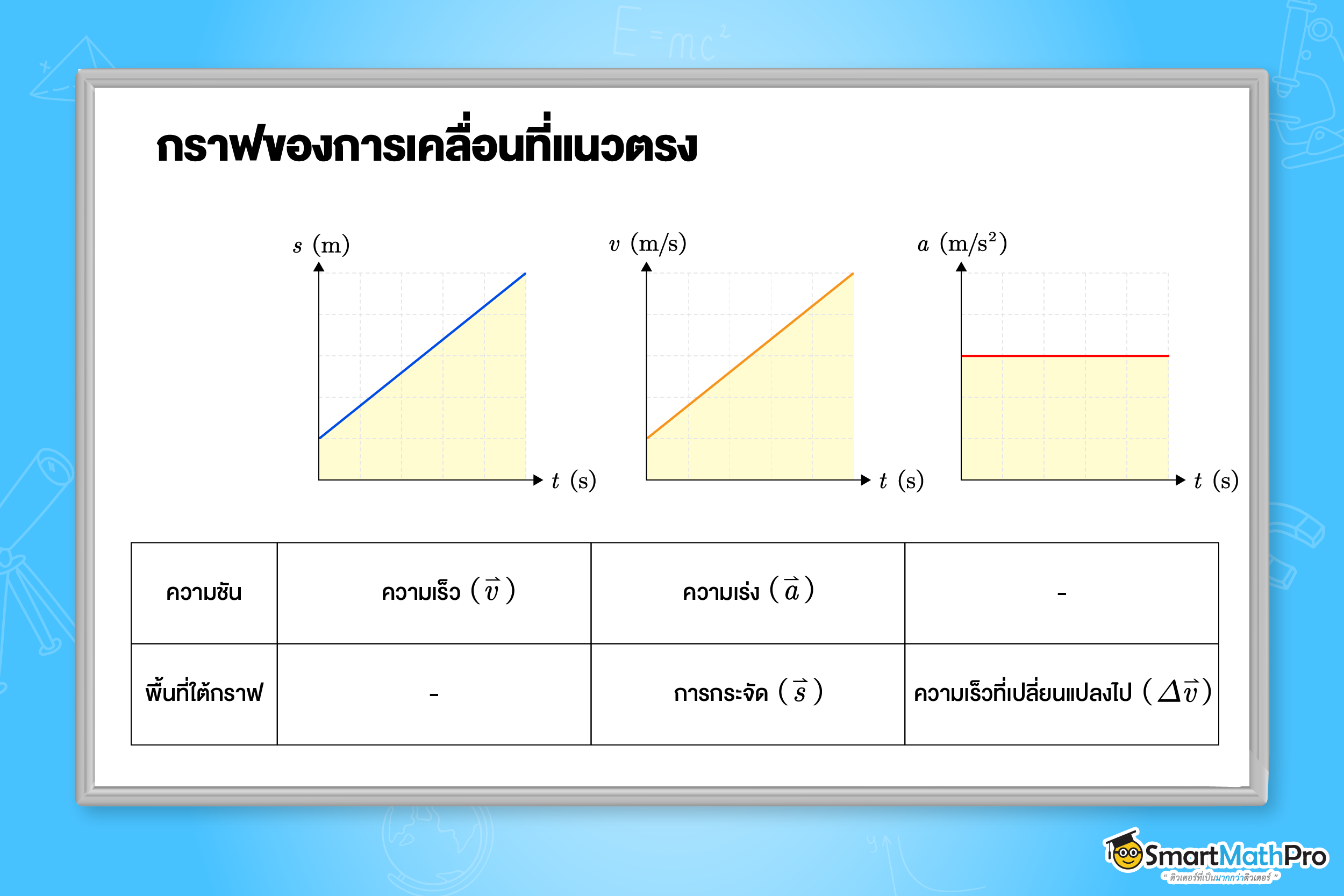
การเคลื่อนที่ในแนวตรงสามารถอธิบายได้ด้วยกราฟ 3 ประเภท ได้แก่ กราฟตำแหน่ง-เวลา, ความเร็ว-เวลา และความเร่ง-เวลา โดยแต่ละกราฟมีความสัมพันธ์กับปริมาณต่าง ๆ ดังนี้

ความรู้เพิ่มเติม สำหรับกราฟความเร็วกับเวลา
ถ้าต้องการหา ระยะทาง จะต้องนำพื้นที่ใต้กราฟทั้งหมดมารวมกัน โดยไม่คำนึงถึงเครื่องหมายบวกหรือลบ นั่นคือให้พื้นที่ที่อยู่ใต้แกนเวลามีค่าเป็นบวกด้วย $+$
ถ้าต้องการหา การกระจัด จะต้องนำพื้นที่ใต้กราฟทั้งหมดมารวมกัน โดยคำนึงถึงเครื่องหมายบวกและลบ นั่นคือพื้นที่ใต้กราฟที่อยู่เหนือแกนนอน มีค่าเป็นบวก $+$ พื้นที่ใต้กราฟที่อยู่ใต้แกนนอน มีค่าเป็นลบ $-$

ตัวอย่างโจทย์ : กราฟของการเคลื่อนที่แนวตรง

1. กราฟระหว่างตำแหน่งกับเวลาของวัตถุหนึ่ง ดังรูป จงหาความเร็วของวัตถุ

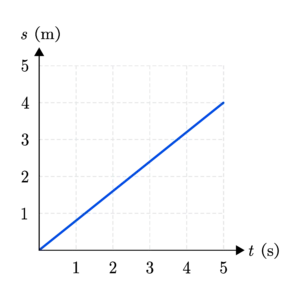
วิธีทำ
หาความเร็วของวัตถุ ได้จากความชันของกราฟ
$m=\frac{\Delta y}{\Delta x} \\ m=\frac{4-0}{5-0} \\ m=0.8\text{ m/s}$
ตอบ ความเร็วของวัตถุเท่ากับ $0.8$ เมตรต่อวินาที

2. กราฟระหว่างความเร็วกับเวลาของวัตถุหนึ่ง ดังรูป จงหาระยะทางในการเคลื่อนที่ทั้งหมด

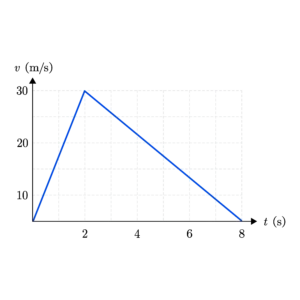
วิธีทำ

หาระยะทางในการเคลื่อนที่ ได้จากพื้นที่ใต้กราฟ
พื้นที่ใต้กราฟ $=\frac{1}{2}\times 8\times 30$
พื้นที่ใต้กราฟ $=120\text{ m}$

ตอบ ระยะทางในการเคลื่อนที่ทั้งหมดเท่ากับ $120$ เมตร

การเคลื่อนที่อย่างอิสระภายใต้แรงโน้มถ่วงของโลก

การตกแบบอิสระ คือ การที่วัตถุตกลงสู่พื้นด้วยความเร่งเนื่องจากแรงโน้มถ่วงของโลกเพียงแรงเดียว ซึ่งความเร่งของวัตถุที่ตกจะไม่ขึ้นอยู่กับชนิด มวล หรือรูปร่างของวัตถุ
ความเร่งโน้มถ่วงของโลกมีค่าประมาณ $9.8$ เมตรต่อวินาทียกกำลังสอง และมีทิศพุ่งลงสู่พื้นโลก

การเคลื่อนที่ในแนวดิ่ง
การโยนวัตถุขึ้นในแนวดิ่ง วัตถุจะเคลื่อนที่ช้าลงเรื่อย ๆ เนื่องจากความเร่งมีทิศทางตรงข้ามกับความเร็ว จนถึงจุดสูงสุดวัตถุจะหยุดนิ่งชั่วขณะหนึ่ง

ก่อนจะเปลี่ยนทิศทางเคลื่อนที่ลง แล้ววัตถุจะมีความเร็วเพิ่มขึ้นเรื่อย ๆ เนื่องจากความเร่งโน้มถ่วงมีทิศทางเดียวกับความเร็ว

ที่จุดสูงสุดความเร็วมีค่าเท่ากับ $0$
เวลาที่ใช้เคลื่อนที่ขึ้น เท่ากับเวลาที่ใช้เคลื่อนที่ลง
ที่ระดับเดียวกัน ความเร็วมีขนาดเท่ากันแต่ทิศทางตรงกันข้าม

การเคลื่อนที่ในแนวดิ่งสามารถใช้สมการเดียวกันกับการเคลื่อนที่ในแนวตรง แต่จะมีความเร่งในแนวดิ่งคงที่เท่ากับความเร่งโน้มถ่วงของโลก

ตัวอย่างโจทย์ : การตกแบบอิสระในแนวดิ่ง

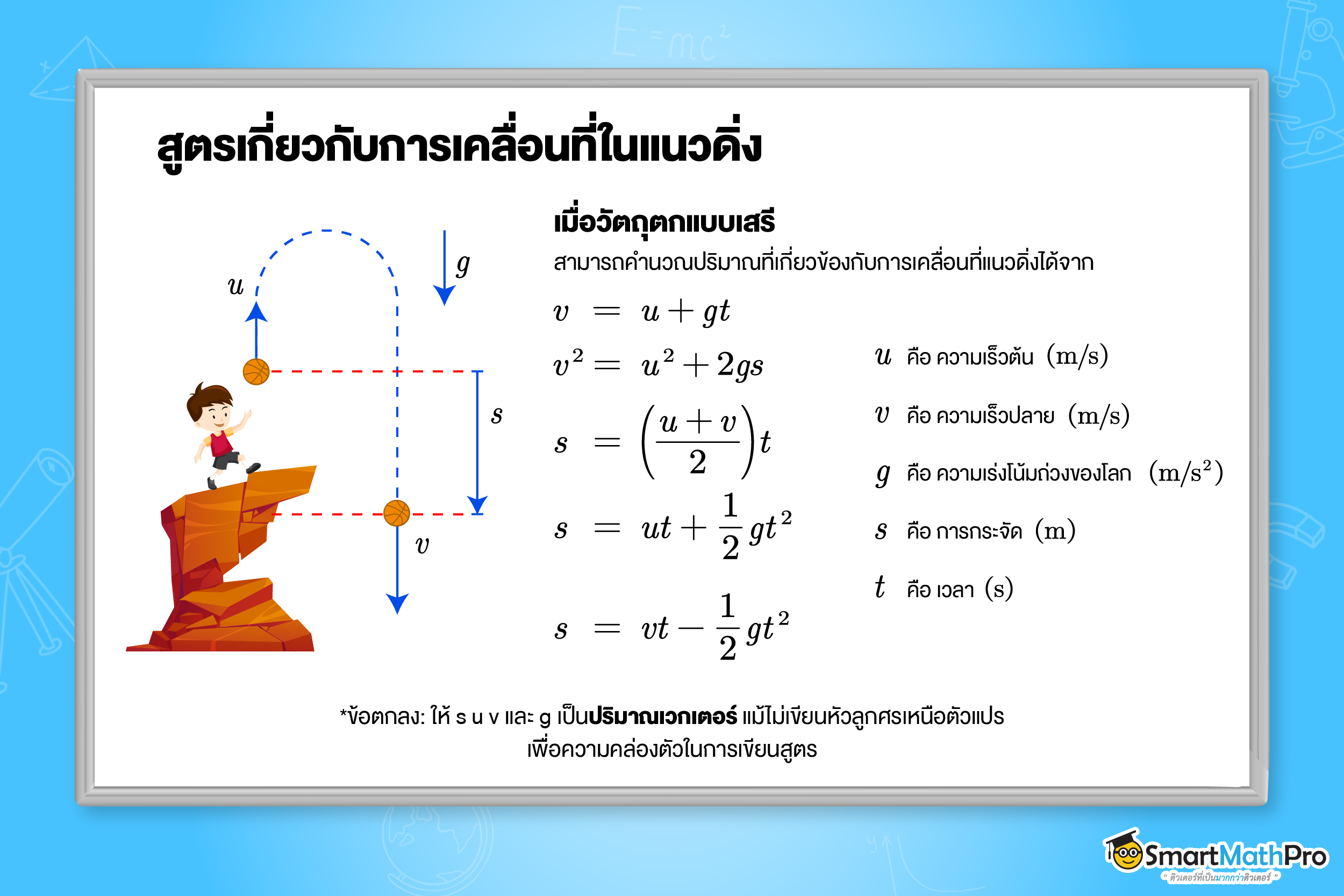
โยนก้อนหินขึ้นไปตามแนวดิ่งด้วยความเร็วต้น $9.8$ เมตรต่อวินาที จงหา
ก. ก้อนหินใช้เวลาเท่าใดจึงจะเคลื่อนที่ถึงจุดสูงสุด
ข. ก้อนหินขึ้นไปได้สูงสุดเท่าใด
ค. เป็นเวลานานเท่าใด ก้อนหินจึงจะตกลงมาถึงตำแหน่งเริ่มต้น

วิธีทำ
ที่จุดสูงสุดความเร็วของก้อนหินมีค่าเท่ากับ $0$
กำหนดให้ ทิศทางเดียวกับความเร็วต้นเป็นบวก และทิศตรงกันข้ามกับความเร็วต้นเป็นลบ
ก. ก้อนหินใช้เวลาเท่าใดจึงจะเคลื่อนที่ถึงจุดสูงสุด
$v=u+gt \\ 0=9.8+(-9.8)t \\ t=\frac{9.8}{9.8} \\ t=1 \text{ s}$
ตอบ ก้อนหินเคลื่อนที่ถึงจุดสูงสุดใช้เวลา $1$ วินาที

ข. ก้อนหินขึ้นไปได้สูงสุดเท่าใด
ณ ตำแหน่งสูงสุด วัตถุจะมีความเร็วเป็นศูนย์
$v^{2}=u^{2}+2gs \\ 0=(9.8)^{2}+2(-9.8)s \\ s=\frac{96.04}{19.6} \\ s=4.9\text{ m}$
ตอบ ก้อนหินขึ้นไปได้สูงสุด $4.9$ เมตร

ค. เป็นเวลานานเท่าใด ก้อนหินจึงจะตกลงมาถึงตำแหน่งเริ่มต้น
ณ ตำแหน่งเริ่มต้น การกระจัดของวัตถุเท่ากับ $0$ เมตร
$s=ut+\frac{1}{2}gt^{2} \\ 0=9.8t+\frac{1}{2}(-9.8)t^{2} \\ 4.9t^{2}=9.8t \\ t^{2}=2t \\ t^{2}-2t=0 \\ t(t-2)=0 \\ t=0\text{ s},2\text{ s}$
ตอบ ก้อนหินจึงจะตกลงมาถึงตำแหน่งเริ่มต้นเมื่อเวลาผ่านไป $2$ วินาที

ความรู้เพิ่มเติม เวลา $t$ มีสองคำตอบได้แก่ $0$ วินาทีและ $2$ วินาที
เนื่องจาก $0$ วินาที แสดงเวลาตอนเริ่มต้น
และ $2$ วินาที แสดงเวลาการเคลื่อนที่ทั้งหมดจนตกกลับลงมาถึงตำแหน่งเริ่มต้น

เก็บเนื้อหา A-Level ฟิสิกส์ให้แม่นกับ SmartMathPro

สำหรับสนามสอบ A-Level ก็จะเป็นอีกสนามที่มีความสำคัญมากเพราะสามารถใช้ยื่นคะแนนได้หลายคณะและเป็นวิชาที่ต้องอาศัยการเตรียมตัวค่อนข้างนาน สำหรับใครที่กลัวเตรียมตัวไม่ทันอยากจะประหยัดเวลาในการเตรียมสอบ

พี่ขอแนะนำคอร์สเรียนพิเศษสนาม A-Level ของ SmartMathPro ที่มีทั้ง A-Level คณิต 1,2 /
A-Level ภาษาอังกฤษ / A-Level ฟิสิกส์ / A-Level ภาษาไทย / A-Level สังคม เลยน้าา

โดยสำหรับใครที่ไม่มีพื้นฐานก็สามารถเรียนได้ เพราะพี่สอนตั้งแต่ปูพื้นฐาน ไปจนถึงพาทำโจทย์ตั้งแต่ระดับง่ายไปจนถึงความยากใกล้เคียงกับข้อสอบจริงเลย แถมมีเทคนิคในการทำข้อสอบอีกเพียบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้น > <

และสำหรับใครที่ยังไม่เริ่ม เริ่มติวตอนนี้ก็ยังทันน้าา แอบกระซิบว่าถ้าสมัครคอร์สตั้งแต่ตอนนี้พี่มี Unseen Mock Test ชุดพิเศษ 1 ชุด แถมฟรีไปให้ลองทำพร้อมสิทธิพิเศษประจำเดือนอีกมากมายด้วย ถ้าน้อง ๆ คนไหนสนใจคอร์สเตรียมสอบ A-Level สามารถ คลิก เข้ามาดูรายละเอียดได้เลยย

ข้อสอบการเคลื่อนที่แนวตรงพร้อมเฉลย

อธิบายเฉลยข้อสอบเกี่ยวกับการเคลื่อนที่แนวตรง

วิธีทำ
หาความเร่งของวัตถุ
$s=vt-\frac{1}{2}gt^{2} \\ 75=2(10)-\frac{1}{2}a(10)^{2} \\ 75=20-50a \\ 55=-50a \\ a=\frac{55}{-50} \\ a=-1.1\text{ m/s}^{2}$
ตอบ ขนาดความเร่งของวัตถุเท่ากับ $1.1$ เมตรต่อวินาทียกกำลังสอง (ตัวเลือกที่ 3)

อธิบายเฉลยข้อสอบเกี่ยวกับการเคลื่อนที่แนวตรง

วิธีทำ
ณ ตำแหน่งสูงสุด วัตถุจะมีความเร็วเป็นศูนย์
กำหนดให้ ทิศทางเดียวกับความเร็วต้นเป็นบวก และทิศตรงกันข้ามกับความเร็วต้นเป็นลบ
หาความสูงที่วัตถุขึ้นไปได้
$v^{2}=u^{2}+2gs \\ 0=7^{2}+2(-9.8)s \\ 19.6s=49 \\ s=\frac{49}{19.6} \\ s=2.5\text{ m}$
ตอบ วัตถุขึ้นไปได้สูง $2.5$ เมตร (ตัวเลือกที่ 3)

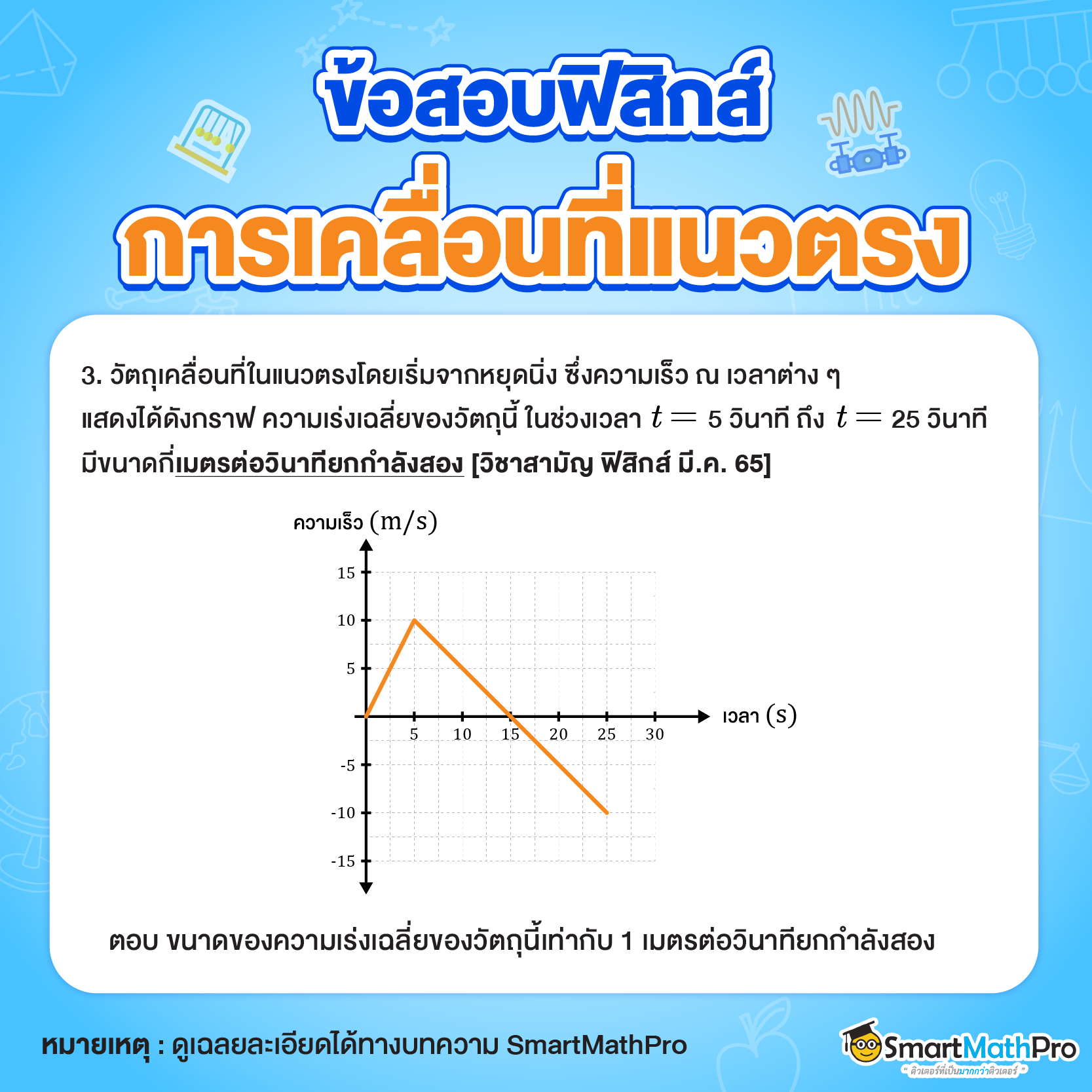
อธิบายเฉลยข้อสอบเกี่ยวกับการเคลื่อนที่แนวตรง

วิธีทำ
หาความเร่งเฉลี่ย ในช่วงเวลา t = 5 วินาที ถึง t = 25 วินาที
ได้จากความชันของกราฟ

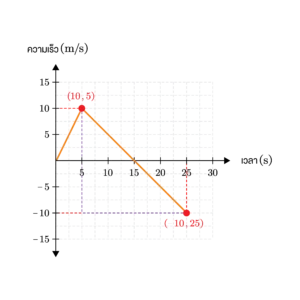
$m=\frac{\Delta y}{\Delta x} \\ m=\frac{(-10)-10}{25-5} \\ m=\frac{-20}{20} \\ m=-1 \text{ m/s}^{2} \\ a=-1 \text{m/s}^{2}$
ตอบ ขนาดของความเร่งเฉลี่ยของวัตถุนี้เท่ากับ $1$ เมตรต่อวินาทียกกำลังสอง

เป็นอย่างไรกันบ้างกับ “สรุปเนื้อหาเรื่อง การเคลื่อนที่แนวตรง ฟิสิกส์ ม.4” และแนวข้อสอบที่พี่นำมาฝากในวันนี้ แนะนำว่าถ้าใครอยากจะแม่นเนื้อหาเรื่องนี้ นอกจากก็อ่านเนื้อหาแล้ว ก็ควรฝึกทำแบบฝึกหัดหรือข้อสอบเก่าเรื่องนี้บ่อย ๆ ด้วยย