สรุป ฟิสิกส์นิวเคลียร์ ม.6 พร้อมโจทย์และเฉลย

สำหรับน้อง ๆ ม.ปลายที่กำลังมองหาสรุปเนื้อหาฟิสิกส์นิวเคลียร์ ม.6 ไม่ควรพลาดบทความนี้เลยน้าา เพราะว่าพี่เตรียมสรุปทั้งความหมาย เสถียรภาพของนิวเคลียส, กัมมันตภาพรังสี, Half life, ปฏิกิริยานิวเคลียร์และพลังงานนิวเคลียร์ พร้อมมีตัวอย่างโจทย์ให้แต่ละหัวข้อด้วย และท้ายบทความมีแบบฝึกหัดและเฉลยแจกให้ไปฝึกเพิ่มเติมกันด้วยน้า

สนใจหัวข้อไหน ... กดอ่านเลย

ฟิสิกส์นิวเคลียร์คืออะไร ?

ฟิสิกส์นิวเคลียร์ (Nuclear Physics) คือ สาขาหนึ่งของวิชาฟิสิกส์ที่ศึกษานิวเคลียสของอะตอม โครงสร้าง องค์ประกอบ และปฏิกิริยาที่เกิดขึ้นภายใน เช่น การสลายกัมมันตรังสี การรวมตัว และการแตกตัวของนิวเคลียส เป้าหมายหลักคือทำความเข้าใจแรงนิวเคลียร์และปฏิสัมพันธ์ระหว่างโปรตอน–นิวตรอน

ตลอดจนปัจจัยที่กำหนดความเสถียรของนิวเคลียส ความรู้เหล่านี้เป็นพื้นฐานของการประยุกต์ในหลายสาขา เช่น พลังงาน การแพทย์ วิศวกรรมวัสดุ อุตสาหกรรม ชีววิทยา ธรณีวิทยา และโบราณคดี

เสถียรภาพของนิวเคลียส

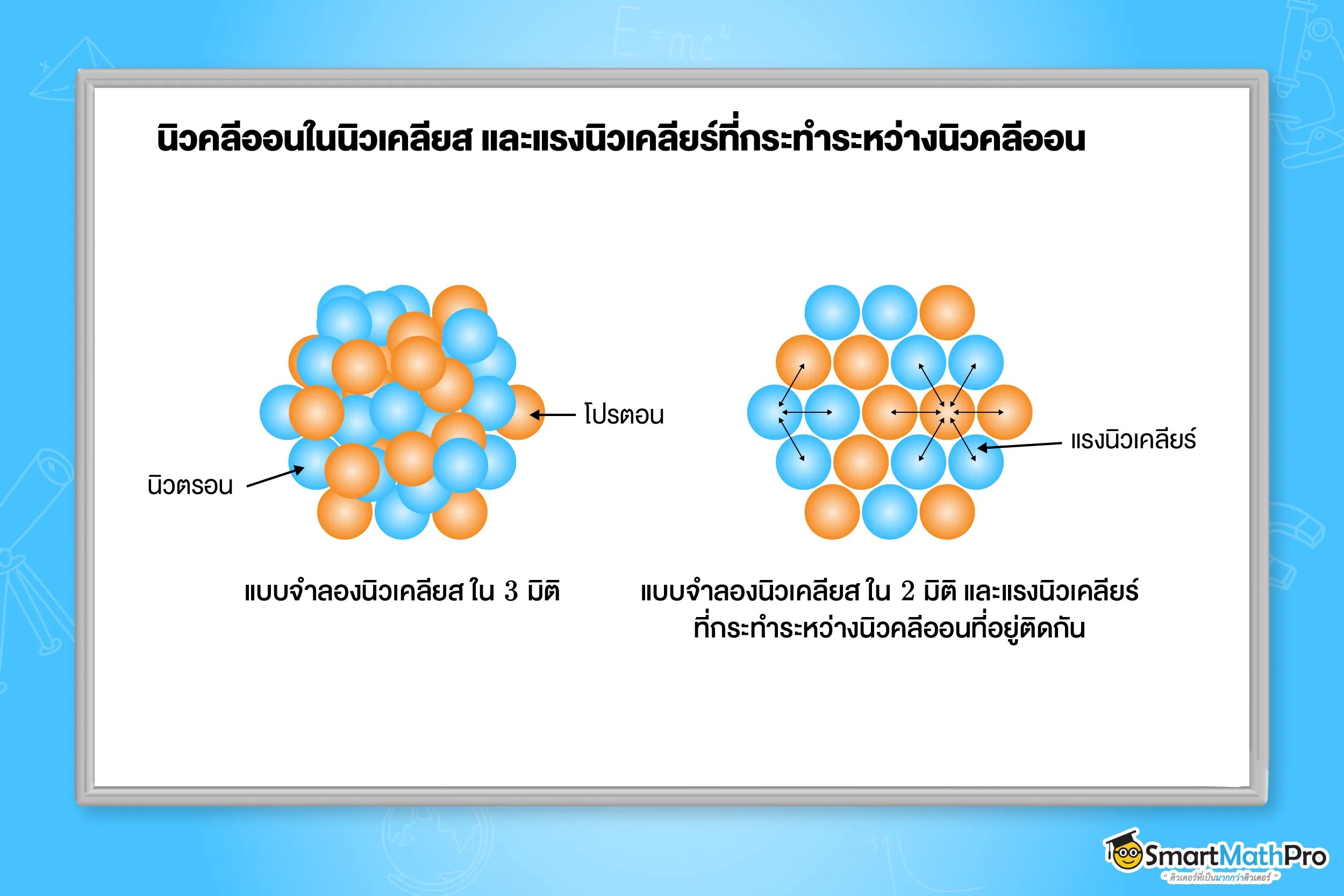
ภายในนิวเคลียส มีโปรตอนที่มีประจุไฟฟ้าบวกและนิวตรอนที่เป็นกลางทางไฟฟ้าอยู่รวมกัน เรียกอนุภาคทั้งสองว่า
นิวคลีออน (nucleon) การที่โปรตอนจำนวนหลายอนุภาคสามารถรวมกันอยู่ได้ภายใน นิวเคลียส

ทั้งที่มีแรงผลักทางไฟฟ้าระหว่างโปรตอน แสดงว่า ต้องมีแรงอีกชนิดหนึ่งที่มีขนาดมากกว่าแรงไฟฟ้า จึงสามารถยึดเหนี่ยวให้โปรตอนในนิวเคลียสรวมกันอยู่ได้

แรงนิวเคลียร์

แรงนิวเคลียร์ คือ แรงดึงดูดระหว่างโปรตอนกับโปรตอน นิวตรอนกับนิวตรอน และโปรตอนกับนิวตรอน ทำให้นิวคลีออนยึดเหนี่ยวรวมกันเป็นนิวเคลียสของอะตอม แรงนิวเคลียร์เป็นแรงระยะสั้นมาก มีบทบาทสำคัญต่อความเสถียรของนิวเคลียส

โดยแรงนี้ไม่ขึ้นกับประจุและมวลของนิวคลีออน จึงมีค่าเท่ากันสำหรับนิวคลีออนทุกคู่ นอกจากนี้ แรงนิวเคลียร์จะกระทำ
เฉพาะนิวคลีออนที่อยู่ติดกันเท่านั้น ไม่ส่งผลต่อนิวคลีออนที่อยู่ถัดออกไป และไม่ส่งผลต่ออิเล็กตรอน

พลังงานยึดเหนี่ยว

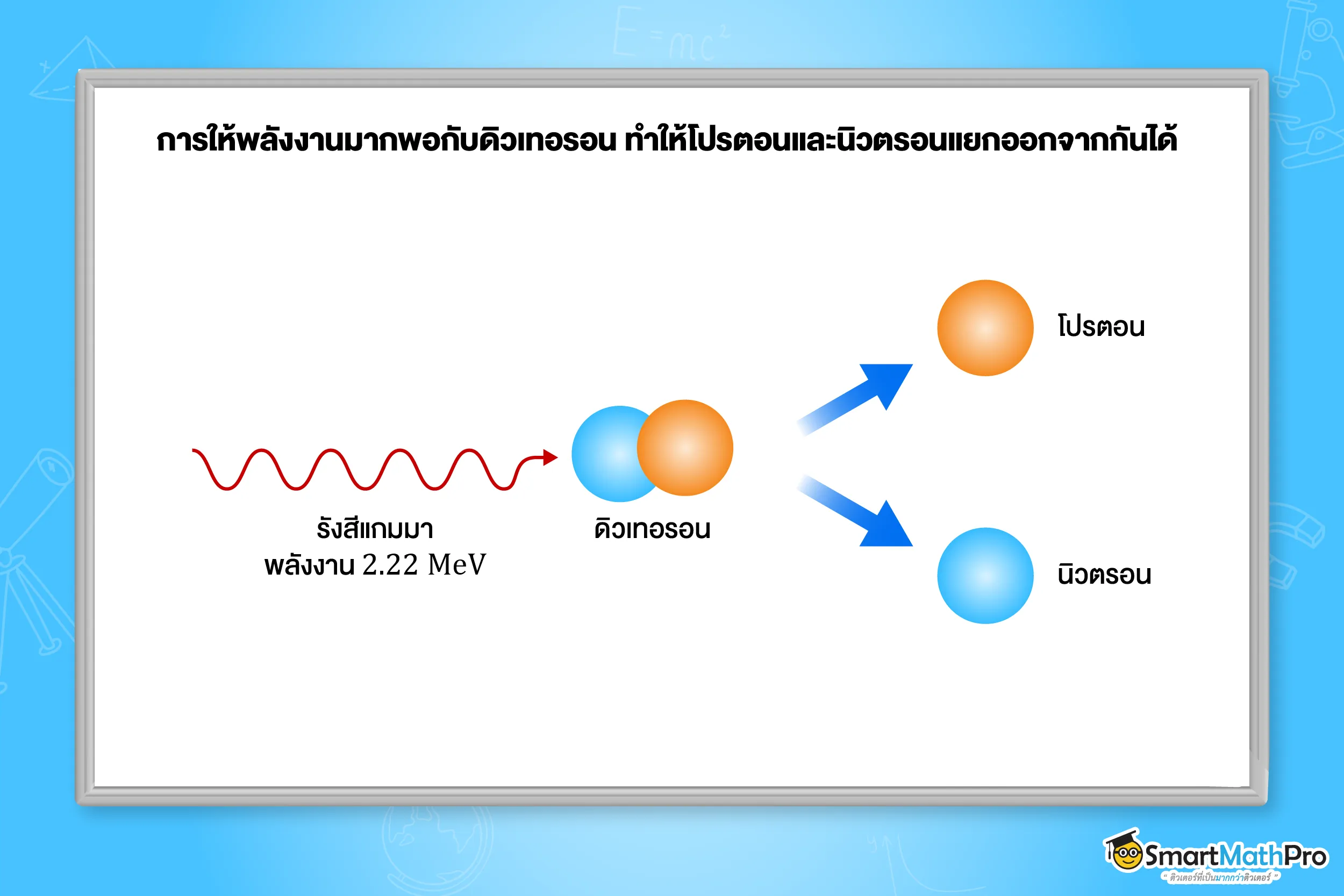
พลังงานยึดเหนี่ยว (Binding Energy) คือ พลังงานที่พอดีทำให้นิวคลีออนทั้งหมดในนิวเคลียสแยกออกจากกัน
เช่น พลังงาน $2.22\text{ MeV}$ เป็นพลังงานที่พอดีในการทำให้โปรตอนและนิวตรอนในดิวเทอรอนแยกออกจากกัน ดังภาพ

ในธรรมชาติ นิวเคลียสของธาตุและไอโซโทปทุกชนิดมีมวล น้อยกว่า มวลรวมของโปรตอนและนิวตรอนที่ประกอบกันเป็นนิวเคลียส เนื่องจากเมื่อนิวคลีออนรวมตัวกัน จะมีมวลบางส่วนเปลี่ยนเป็นพลังงานเพื่อใช้ยึดเหนี่ยวนิวคลีออนให้อยู่ร่วมกันส่งผลให้นิวเคลียสมีเสถียรภาพ

ความแตกต่างระหว่างมวลของนิวเคลียสกับมวลรวมของนิวคลีออนเรียกว่า ส่วนพร่องมวล $\Delta m$ มีค่าเทียบเท่ากับ พลังงานยึดเหนี่ยวของนิวเคลียส ตามความสัมพันธ์

$E=(\Delta m)c^{2}$

โดยมวล $1\ u$ มีค่าเทียบเท่าพลังงานประมาณ $931.5\text{ MeV}$

$E=(\Delta m)(931.5 \text{ MeV/u})$

เนื่องจากมวลของนิวเคลียสไม่ค่อยระบุในตารางข้อมูลทั่วไป การคำนวณส่วนพร่องมวลจึงนิยมใช้ผลต่างระหว่าง มวลรวมขององค์ประกอบอะตอม กับ มวลอะตอมของธาตุ ซึ่งมวลของอิเล็กตรอนจะหักล้างกันพอดี ทำให้สามารถนำส่วนพร่องมวลไปคำนวณพลังงานยึดเหนี่ยวของนิวเคลียสได้โดยตรง

ดังนั้น สามารถหาส่วนพร่องมวลของนิวเคลียส $^{A}_{Z}\mathrm{X}$ ได้จาก

$\Delta m = m_{total}-m_{atom}$

$\Delta m =\left[Zm_{p}+(A-Z)m_{n}+Zm_{e}\right]-m_{atom}$

โดย $m_{p}$ คือ มวลของโปรตอน
$m_{n}$ คือ มวลของนิวตรอน
$m_{e}$ คือ มวลของอิเล็กตรอน
$m_{total}$ คือ มวลรวมขององค์ประกอบอะตอม
$m_{atom}$ คือ มวลอะตอม

นิวเคลียสที่มีจำนวนนิวคลีออนมาก มักมีพลังงานยึดเหนี่ยวรวมมากกว่านิวเคลียสที่มีนิวคลีออนน้อย อย่างไรก็ตาม การมีพลังงานยึดเหนี่ยวรวมมาก ไม่ได้หมายความว่านิวเคลียสจะมีเสถียรภาพมากกว่าเสมอไป เนื่องจากในธรรมชาติ นิวเคลียสที่มีเลขอะตอมมากกว่า 83 ล้วนไม่เสถียร

ดังนั้น การพิจารณาความเสถียรของนิวเคลียสจึงต้องใช้ พลังงานยึดเหนี่ยวต่อนิวคลีออน ซึ่งเป็นพลังงานเฉลี่ยที่ต้องใช้ในการแยกนิวคลีออนแต่ละตัวออกจากนิวเคลียส คำนวณได้จากสมการ

$\frac{E}{A}=\frac{(\Delta m)c^{2}}{A}$

หรือ เมื่อพิจารณา $\Delta m$ ในหน่วย $u$ จะได้

$\frac{E}{A}=\frac{(\Delta m)(\text{931.5 MeV})}{A}$

พลังงานยึดเหนี่ยวต่อนิวคลีออนมีหน่วยเป็น จูลต่อนิวคลีออน $(\text{J/nucleon})$ หรือ เมกะอิเล็กตรอนโวลต์ต่อนิวคลีออน $(\text{MeV/nucleon})$ โดยค่ายิ่งมาก แสดงว่านิวเคลียสยิ่งมีเสถียรภาพ

เมื่อเขียนกราฟระหว่างพลังงานยึดเหนี่ยวต่อนิวคลีออน $(\frac{E}{A})$ กับเลขมวล $(A)$ จะได้กราฟแสดงแนวโน้มความเสถียรของนิวเคลียสตามเลขมวล ดังภาพ

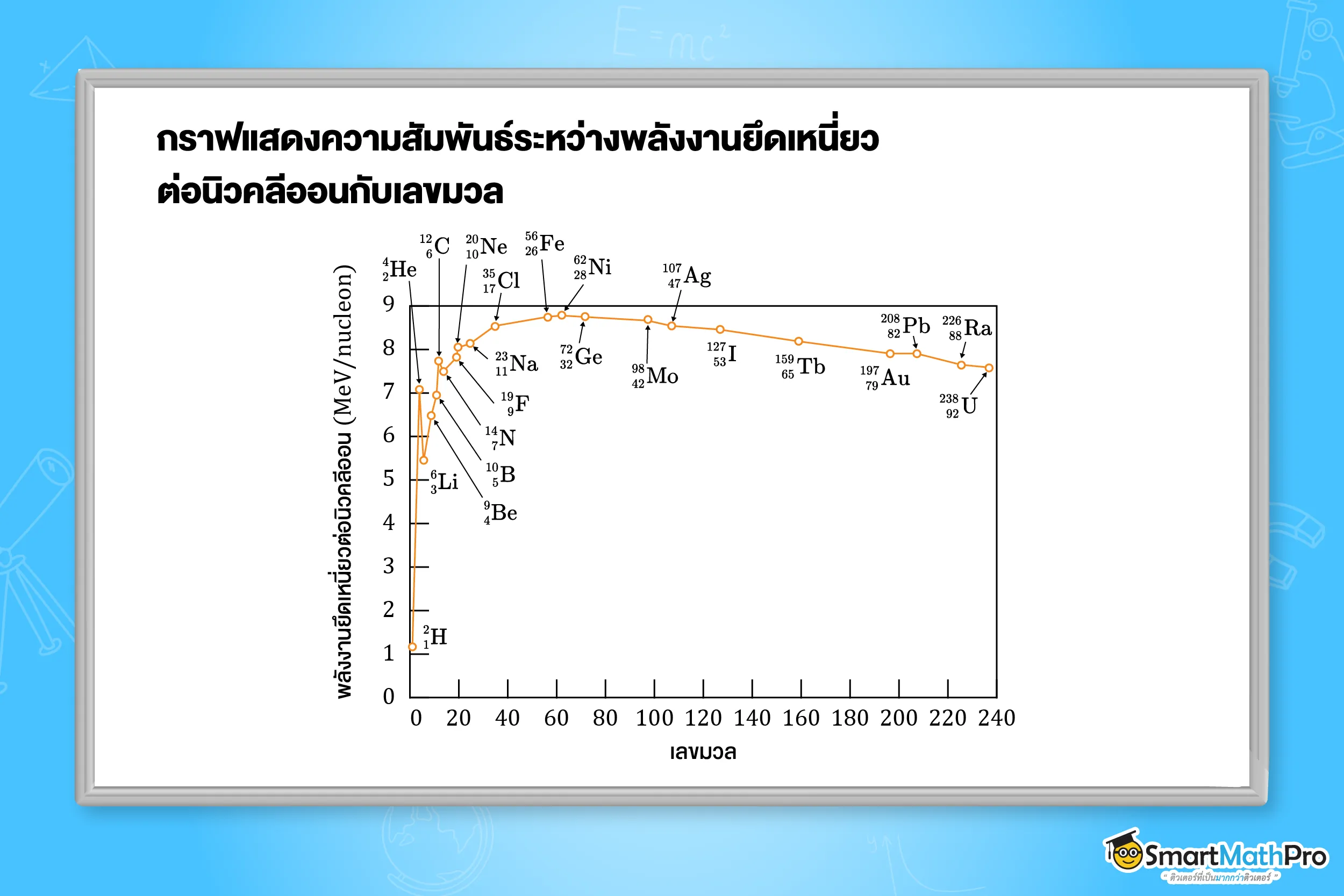
จากกราฟพบว่า นิวเคลียสที่มีเลขมวลประมาณ $55-70$ มีพลังงานยึดเหนี่ยวต่อนิวคลีออนสูงกว่านิวเคลียสช่วงอื่น โดยเฉพาะ นิกเกิล (Ni) ซึ่งมีค่ามากที่สุด แสดงว่านิวเคลียสในช่วงนี้มีความเสถียรสูง และต้องใช้พลังงานมากในการแยกนิวคลีออนออกจากกัน

ตัวอย่างโจทย์เกี่ยวกับเสถียรภาพของนิวเคลียส

จงคำนวณหาพลังงานยึดเหนี่ยวเฉลี่ยต่อหนึ่งนิวคลีออนของนิวเคลียสคาร์บอน $-12$ $(^{12}_{6}\mathrm{C})$ ในหน่วยเมกะอิเล็กตรอนโวลต์
กำหนดให้ มวล $1\text{ u} = 1.66×10^{-27} \text{ kg}$ เทียบเท่ากับพลังงาน $931.5 \text{ MeV}$

มวลของโปรตอน $(m_{p})=1.007276 \text{ u}$
มวลของนิวตรอน $(m_{n})=1.008665\text{ u}$
มวลของอิเล็กตรอน $(m_{e})=0.000549 \text{ u}$
มวลอะตอมของ คาร์บอน $(^{12}_{6}\mathrm{C})=12.000000 \text{ u}$

วิธีทำ
อะตอมของคาร์บอน $(^{12}_{6}\mathrm{C})$ ประกอบด้วยโปรตอน $6$ โปรตอน นิวตรอน $6$ นิวตรอน และ อิเล็กตรอน $6$ อิเล็กตรอน

หามวลรวมขององค์ประกอบของอะตอม $(^{12}_{6}\mathrm{C})$

$m_{total}=6m_{p}+6m_{n}+6m_{e}$

$=61.007276 \text{ u}+61.008665 \text{ u}+60.000549 \text{ u}$

$=12.098940 \text{ u}$

หาส่วนพร่องมวลอะตอมของคาร์บอน
จาก $\Delta m = m_{total}-m_{atom}$
แทนค่า $\Delta m=12.098940 \text{ u}-12.000000 \text{ u}$
$=0.098940 \text{ u}$

หาพลังงานยึดเหนี่ยวที่เทียบเท่ากับส่วนพร่องมวล
จาก $E=(∆m)c^{2}$
แทนค่า $E=0.098940(931.5)$
$=92.16\text{ MeV}$

จาก $\frac{E}{A}=\frac{(\Delta m)c^{2}}{A}$
แทนค่า $\frac{E}{A}=\frac{92.162610}{12}$
$=7.68 \text{ MeV/nucleon}$

ตอบ พลังงานยึดเหนี่ยวเฉลี่ยต่อหนึ่งนิวคลีออนของนิวเคลียสคาร์บอน $-12$ เท่ากับ $7.68$ เมกะอิเล็กตรอนโวลต์

กัมมันตภาพรังสี

การค้นพบกัมมันตภาพรังสี

ปี ค.ศ. 1896 อองตวน อองรี แบ็กเกอแรลค้นพบโดยบังเอิญว่าสารประกอบของยูเรเนียมสามารถปล่อยรังสีออกมาได้เองโดยไม่ต้องใช้พลังงานจากภายนอก

รังสีดังกล่าวสามารถทะลุผ่านวัตถุทึบแสง ทำให้ฟิล์มถ่ายภาพเกิดรอยดำ และมีสมบัติคล้ายรังสีเอกซ์ เช่น ทำให้อากาศแตกตัวเป็นไอออน แต่แตกต่างตรงที่เกิดขึ้นได้เองตามธรรมชาติ

ต่อมา ปีแอร์ กูรี และมารี กูรี ได้ค้นพบธาตุที่แผ่รังสีได้เองเพิ่มเติม คือ เรเดียมและพอโลเนียม ปรากฏการณ์ที่ธาตุสามารถแผ่รังสีออกมาได้เองเรียกว่า กัมมันตภาพรังสี (radioactivity) ไอโซโทปที่แผ่รังสีได้เรียกว่า ไอโซโทปกัมมันตรังสี และธาตุที่ทุกไอโซโทปเป็นกัมมันตรังสีเรียกว่า ธาตุกัมมันตรังสี ซึ่งส่วนใหญ่มักเป็นธาตุที่มีเลขอะตอมมากกว่า $82$ การค้นพบนี้ถือเป็นรากฐานสำคัญของการศึกษาฟิสิกส์นิวเคลียร์

รังสีจากธาตุและไอโซปกัมมันตรังสี

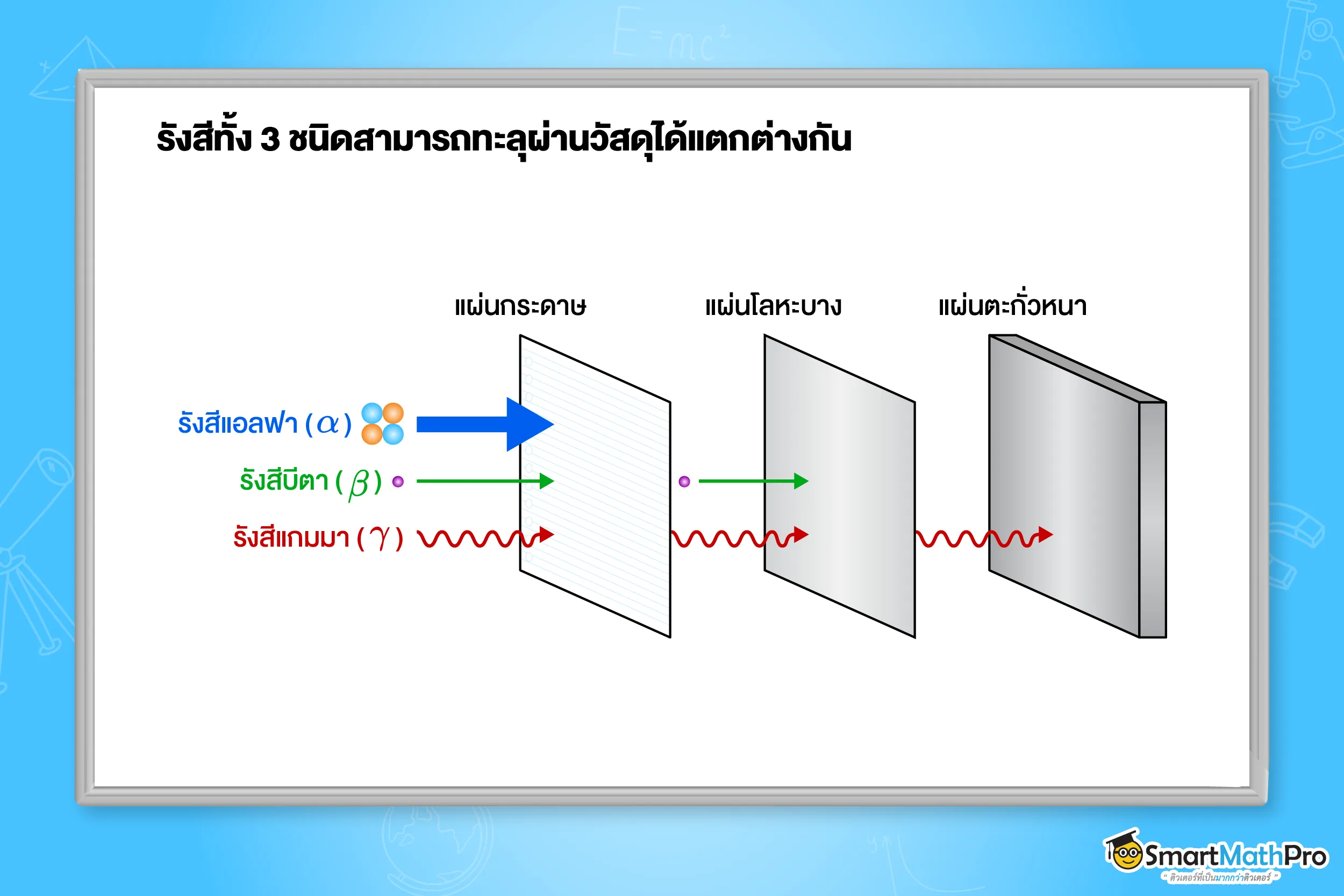
ธาตุและไอโซโทปกัมมันตรังสีส่วนใหญ่มีการแผ่รังสีออกมาอยู่ $3$ ) ชนิด ดังนี้

รังสีแอลฟา (alpha rays, ) เป็นนิวเคลียสของฮีเลียมที่เคลื่อนที่ด้วยความเร็วสูง อาจเรียกอีกชื่อว่า อนุภาคแอลฟามีประจุไฟฟ้า $+2e$ และ ประกอบด้วยโปรตอนและนิวตรอนอย่างละ $2$ อนุภาค
รังสีบีตา (beta rays, ) เป็นอิเล็กตรอนที่เคลื่อนที่ด้วยความเร็วสูง อาจเรียกอีกชื่อว่าอนุภาคบีตา (beta particle) มีประจุไฟฟ้า $-1e$
รังสีแกมมา (gamma rays, ) เป็นคลื่นแม่เหล็กไฟฟ้าหรือโฟตอนที่เป็นกลางทางไฟฟ้าและมีความถี่สูงมาก

เมื่อให้รังสีผ่านเข้าไปในบริเวณที่มีสนามแม่เหล็กจะมีแนวการเคลื่อนที่ ดังภาพ

สลายและสมการการสลาย

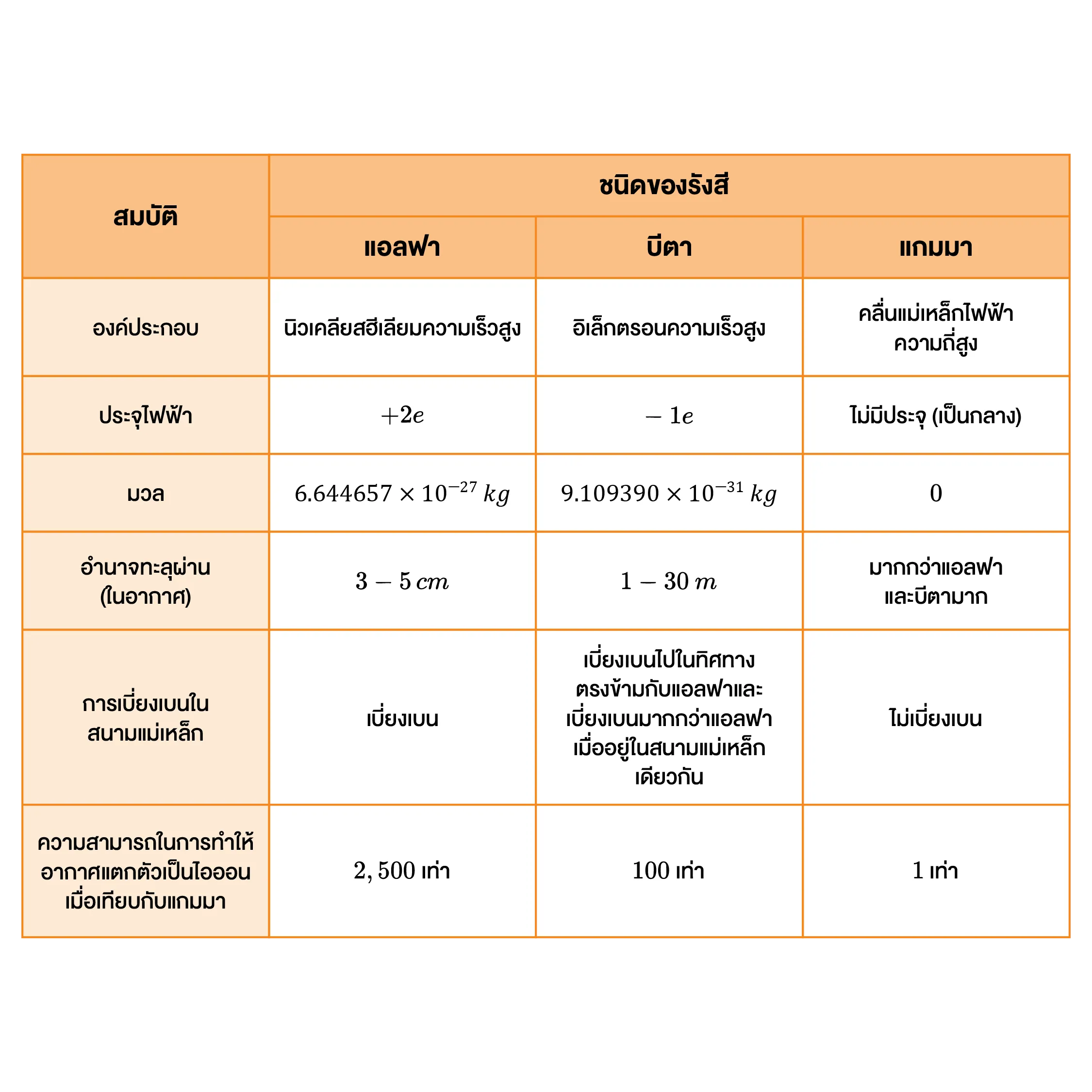
การสลายกัมมันตรังสี (radioactive decay) คือกระบวนการที่นิวเคลียสซึ่งไม่เสถียรเปลี่ยนไปเป็นนิวเคลียสชนิดใหม่หรือเข้าสู่ระดับพลังงานที่ต่ำกว่าเดิม โดยสามารถแผ่รังสีออกมาได้เองตามธรรมชาติ นิวเคลียสที่เกิดการสลายเรียกว่า นิวเคลียสกัมมันตรังสี (radioactive nucleus) การสลายของนิวเคลียสสามารถอธิบายได้ด้วย สมการแสดงสัญลักษณ์นิวเคลียร์ ซึ่งแสดงชนิดของธาตุและอนุภาคก่อนและหลังการสลาย โดยยึดหลักสำคัญคือ ผลรวมของเลขอะตอมและผลรวมของเลขมวลก่อนและหลังการสลายต้องมีค่าเท่ากัน

การสลายกัมมันตรังสีแบ่งออกเป็น 3 ชนิด ได้แก่

การสลายให้แอลฟา (alpha decay)
เมื่อนิวเคลียสของธาตุกัมมันตรังสีตั้งต้นสลายตัวโดยการให้รังสีแอลฟา จะส่งผลให้นิวเคลียสของธาตุใหม่มีเลขมวลลดลง $4$ และเลขอะตอมลดลง $2$

สามารถเขียนสมการการสลายตัวได้ ดังนี้

$^{A}_{Z}\mathrm{X}\rightarrow{}^{A-4}_{Z-2}\mathrm{Y}+{}^{4}_{2}\mathrm{He}$

ตัวอย่างเช่น : การสลายตัวให้แอลฟาของยูเรเนียม $-238$

$^{238}_{92}\mathrm{U}\rightarrow{}^{234}_{90}\mathrm{Th}+{}^{4}_{2}\mathrm{He}$

การสลายให้บีตา (beta decay)
การสลายตัวให้รังสีบีตามี 2 รูปแบบหลัก คือ บีตาลบ และ บีตาบวก ซึ่งแต่ละแบบมีการเปลี่ยนแปลงภายในนิวเคลียสที่แตกต่างกัน ดังนี้

การสลายให้บีตาลบ (beta-minus decay, $β^{-}$ )

เกิดขึ้นเมื่อนิวเคลียสมีจำนวนนิวตรอนมากเกินไป นิวตรอนจะเปลี่ยนเป็นโปรตอน พร้อมกับปล่อยอิเล็กตรอน $(β^{-})$ ออกมา ส่งผลให้นิวเคลียสของธาตุใหม่มีเลขมวลคงที่ แต่เลขอะตอมเพิ่มขึ้น $1$

สามารถเขียนสมการการสลายตัวได้ ดังนี้

$^{A}_{Z}\mathrm{X}\rightarrow{}^{A}_{Z+1}\mathrm{Y}+{}^{0}_{-1}\mathrm{e}$

ตัวอย่างเช่น : การสลายตัวให้บีตาลบของคาร์บอน $-14$

$^{14}_{6}\mathrm{C}\rightarrow{}^{14}_{7}\mathrm{N}+{}^{0}_{-1}\mathrm{e}$

การสลายให้บีตาบวก (beta-plus decay, $β^{+}$ )
เกิดขึ้นเมื่อนิวเคลียสมีจำนวนโปรตอนมากเกินไป โปรตอนจะเปลี่ยนเป็นนิวตรอน พร้อมกับปล่อยโพซิตรอน $(β^{+})$ ออกมา ส่งผลให้นิวเคลียสของธาตุใหม่มีเลขมวลคงที่ แต่เลขอะตอมลดลง $1$

สามารถเขียนสมการการสลายตัวได้ ดังนี้

$^{A}_{Z}\mathrm{X}\rightarrow{}^{A}_{Z-1}\mathrm{Y}+{}^{0}_{+1}\mathrm{e}$

ตัวอย่างเช่น : การสลายตัวให้บีตาบวกของไนโตรเจน $-12$

$^{12}_{7}\mathrm{N}\rightarrow{}^{12}_{6}\mathrm{C}+{}^{0}_{+1}\mathrm{e}$

การสลายให้แกมมา (gamma decay)
การปล่อยรังสีแกมมาไม่ทำให้โครงสร้างนิวเคลียสเปลี่ยนแปลง นิวเคลียสยังคงเป็นธาตุเดิมมีเลขมวล $(A)$ และเลขอะตอม $(Z)$ คงที่ แต่เปลี่ยนจากสภาวะกระตุ้น (Excited State) ที่ไม่เสถียร ไปสู่สภาวะพื้นฐาน (Ground State) ที่มีความเสถียรมากขึ้น

สามารถเขียนสมการการสลายตัวได้ ดังสมการ

$^{A}_{Z}\mathrm{X}^{*}\rightarrow{}^{A}_{Z}\mathrm{X}+\gamma$

ตัวอย่างเช่น : การสลายตัวให้แกมมาของเทคนีเชียม $-99$

$^{99}_{43}\mathrm{Tc}^{*}\rightarrow{}^{99}_{43}\mathrm{Tc}+\gamma$

กัมมันตภาพ

กัมมันตภาพ (Activity) คือ อัตราการแผ่รังสีหรืออัตราการสลายตัวของนิวเคลียสในช่วงเวลาหนึ่ง

มีหน่วยเอสไอ (SI) : เบ็กเคอเรล $\text{Bq}$ ซึ่ง $1$ เบ็กเคอเรล หมายถึง การที่นิวเคลียสสลายตัวไป $1$ นิวเคลียสภายในเวลา $1$ วินาที

หน่วยเดิม : คูรี $\text{Ci}$ โดย $1\text{ Ci}=3.7×10^{10} \text{ Bq}$ โดยมีค่าประมาณเท่ากับอัตราการสลายตัวของเรเดียมมวล $1$ กรัม ในทางปฏิบัติ กัมมันตภาพ $1$ คูรีเป็นค่าที่สูงมาก จึงนิยมใช้หน่วยที่เล็กกว่า เช่น มิลลิคูรี $(\text{mCi})$ หรือไมโครคูรี $(\text{Ci})$

การสลายของนิวเคลียสเป็นปรากฏการณ์ที่เกิดขึ้นแบบ สุ่ม (Random) ซึ่งเราไม่สามารถทำนายได้อย่างแม่นยำว่านิวเคลียสใดจะสลายตัวเมื่อใด ความน่าจะเป็นที่นิวเคลียสจะสลายตัวในหนึ่งหน่วยเวลานี้เรียกว่า ค่าคงตัวการสลาย (Decay constant)

ซึ่งเป็นค่าเฉพาะของนิวเคลียสแต่ละชนิด หากนำค่าคงตัวนี้มาคูณกับจำนวนนิวเคลียสที่มีอยู่ขณะนั้น จะได้ความสัมพันธ์เชิงปริมาณ ดังสมการ

$A=λN$

โดย
$A$ คือ กัมมันตภาพ
คือ ค่าคงตัวการสลาย
$N$ คือ จำนวนนิวเคลียสที่มีอยู่ขณะนั้น

ตัวอย่างโจทย์เกี่ยวกับกัมมันตภาพรังสี

นิวเคลียสของเรเดียม $-226\ (^{226}_{88}\mathrm{Ra})$ มีการสลายโดยการปล่อยอนุภาคแอลฟา $1$ ตัวและรังสีแกมมาออกมา จะทำให้ $^{226}_{88}\mathrm{Ra}$ กลายเป็นธาตุใด

$^{218}_{84}\mathrm{Ra}$
$^{222}_{86}\mathrm{Rn}$
$^{230}_{90}\mathrm{Th}$
$^{234}_{92}\mathrm{U}$

วิธีทำ

หาค่าของ $A$ และ $Z$

เขียนสมการการสลายให้แอลฟา $1$ ตัว $^{226}_{88}\mathrm{Ra}\rightarrow{}^{A}_{Z}\mathrm{X}+{}^{2}_{4}\mathrm{He}$ เลขมวลก่อนการสลายมีค่า $226$ ต้องเท่ากับผลรวมของเลขมวลหลังการสลาย
จะได้ $226=A+4$
$A=222$
เลขอะตอมก่อนการสลายมีค่า 88 ต้องเท่ากับผลรวมของเลขอะตอมหลังการสลาย
จะได้ $88=Z+2$
$Z=86$
เขียนสมการการสลายให้แกมมา $^{222}_{86}\mathrm{X}\rightarrow{}^{A}_{Z}\mathrm{X}+\gamma$
การปล่อยรังสีแกมมาไม่ทำให้เลขมวลและเลขอะตอมเปลี่ยนแปลง
จะได้ นิวเคลียสหลังการสลายมีเลขมวล $222$ และเลขอะตอม $86$
ธาตุซึ่งมีเลขอะตอมเท่ากับ $86$ คือ เรดอน

ดังนั้น เมื่อมีการสลายโดยการปล่อยอนุภาคแอลฟา $1$ ตัวและรังสีแกมมาออกมา จะทำให้ $^{226}_{88}\mathrm{Ra}$ กลายเป็นธาตุ $^{222}_{86}\mathrm{Rn}$

ตอบ 2. $^{222}_{86}\mathrm{Rn}$

half-life

ครึ่งชีวิต (half-life) คือ ช่วงเวลาที่จำนวนนิวเคลียสของสารกัมมันตรังสีสลายตัวจนเหลือเพียง ครึ่งหนึ่งของปริมาณเดิม โดยช่วงเวลาครึ่งชีวิตนี้เป็นสมบัติเฉพาะตัวของสารกัมมันตรังสีแต่ละชนิด

เช่น ไอโอดีน $-131$ มีครึ่งชีวิตประมาณ $8$ วัน หมายความว่าเมื่อเวลาผ่านไปครบ $8$ วัน ปริมาณไอโอดีน $-131$ จะเหลือเพียงครึ่งหนึ่งของเดิม และเมื่อผ่านไปอีกทุก ๆ $8$ วัน ปริมาณที่เหลืออยู่จะลดลงเหลือครึ่งหนึ่งของค่าก่อนหน้าอย่างต่อเนื่อง

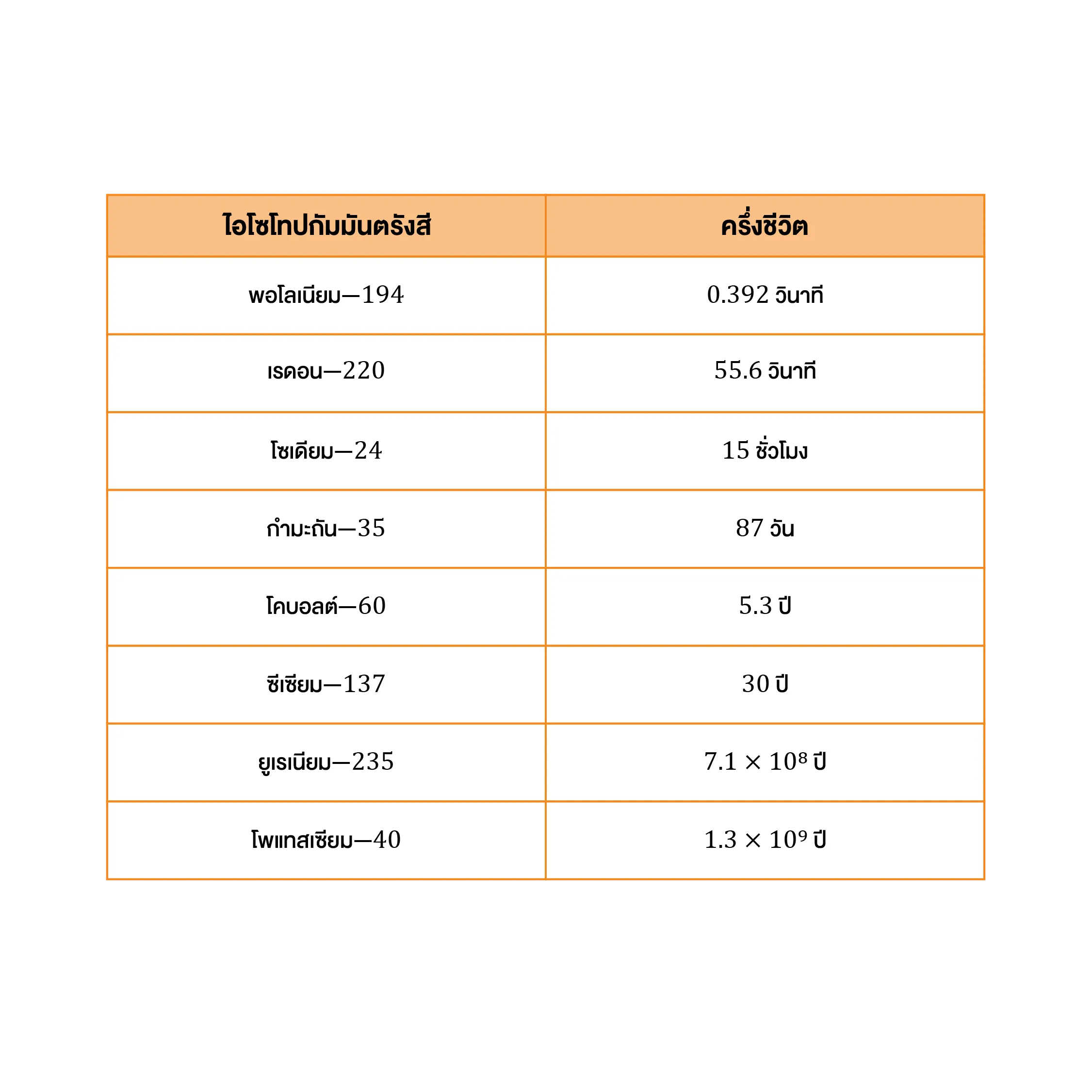
การสลายตัวของนิวเคลียสเป็น กระบวนการแบบสุ่ม ซึ่งนิวเคลียสแต่ละตัวมีโอกาสสลายตัวได้ตลอดเวลา โดยมีลักษณะสำคัญดังนี้

ช่วงเริ่มต้น : เมื่อมีจำนวนนิวเคลียสอยู่มาก อัตราการสลายตัวจะสูงตามไปด้วย
ช่วงเวลาถัดมา : เมื่อจำนวนนิวเคลียสลดลง อัตราการสลายตัวก็จะลดลงในสัดส่วนเดียวกัน
การเปลี่ยนแปลงนี้ส่งผลให้ปริมาณสารลดลงในลักษณะ ฟังก์ชันเอกซ์โพเนนเชียล (Exponential Decay) ดังกราฟ

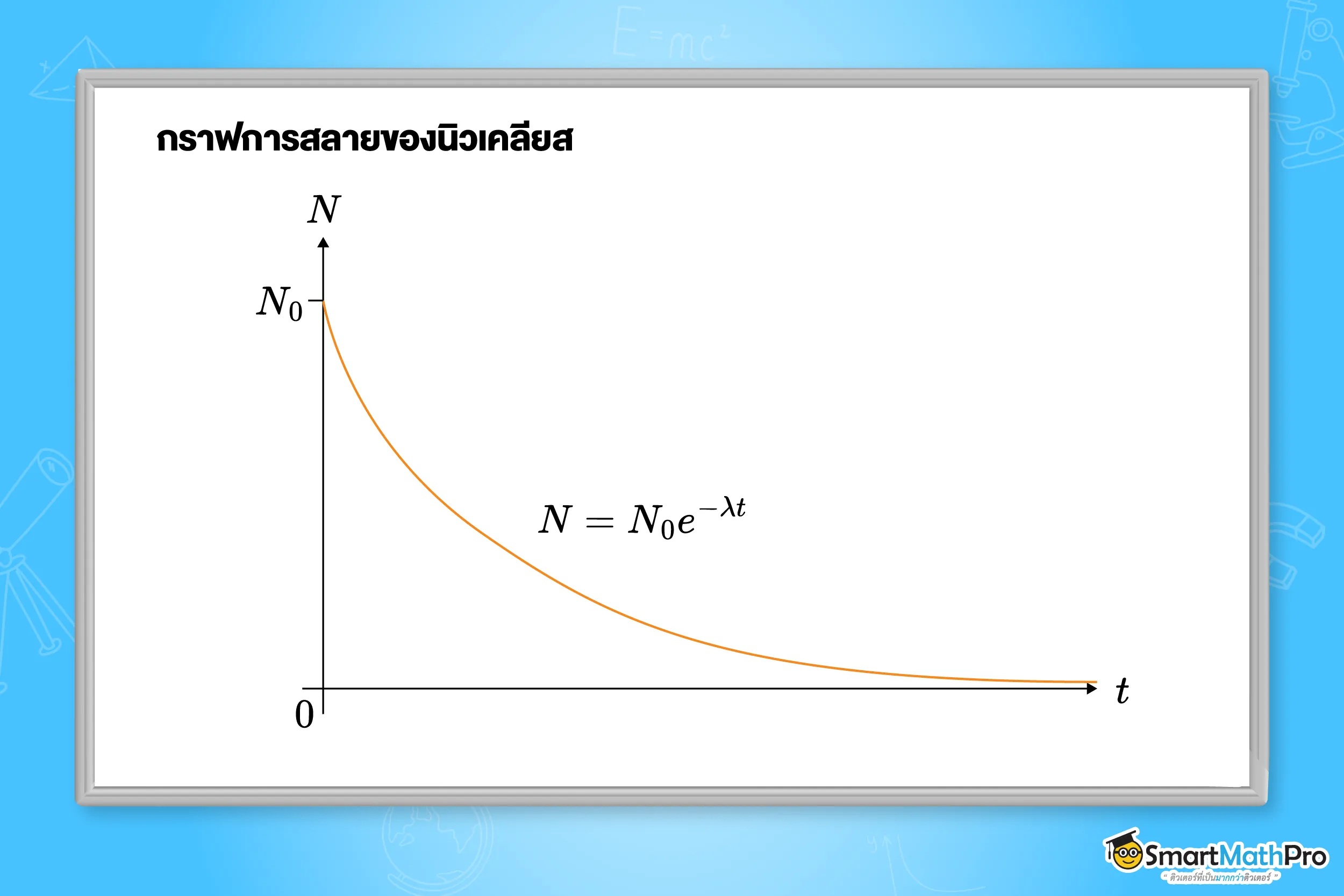
จากกราฟ สามารถเขียนสมการการสลายตัวได้ ดังนี้

$N=N_0e^{-\lambda t}$

โดย $N$ คือ จำนวนนิวเคลียสที่เหลือหลังการสลายเมื่อเวลาผ่านไป $t$
$N_0$ คือ จำนวนนิวเคลียสเริ่มต้น $(t=0)$
$\lambda$ คือ ค่าคงตัวการสลายต่อวินาที

สามารถจัดรูปใหม่ ให้อยู่ในรูปปริมาณอื่นที่เกี่ยวข้องได้ ดังนี้

$A=A_0e^{-\lambda t}$

โดย $A$ คือ กัมมันตภาพที่เหลือหลังการสลายเมื่อเวลาผ่านไป $t$
$A_0$ คือ กัมมันตภาพที่เริ่มต้น $(t=0)$
$\lambda$ คือ ค่าคงตัวการสลายต่อวินาที

$m=m_0e^{-\lambda t}$

โดย $m$ คือ มวลที่เหลือหลังการสลายเมื่อเวลาผ่านไป $t$
$m_0$ คือ มวลเริ่มต้น $(t=0)$
$\lambda$ คือ ค่าคงตัวการสลายต่อวินาที

ในสมการเอกซ์โพเนนเชียลเหล่านี้ ค่าคงตัวการสลาย $(\lambda)$ มีความสัมพันธ์โดยตรงกับครึ่งชีวิต สามารถเขียนความสัมพันธ์ได้ ดังสมการ

$T_{1/2}=\frac{\ln{2}}{\lambda}\approx\frac{0.693}{\lambda}$

นิวเคลียสที่มีค่าคงตัวการสลายมากจะใช้เวลาครึ่งชีวิตสั้น ส่วนนิวเคลียสที่มีค่าคงตัวการสลายน้อยจะใช้เวลาครึ่งชีวิตยาวนาน
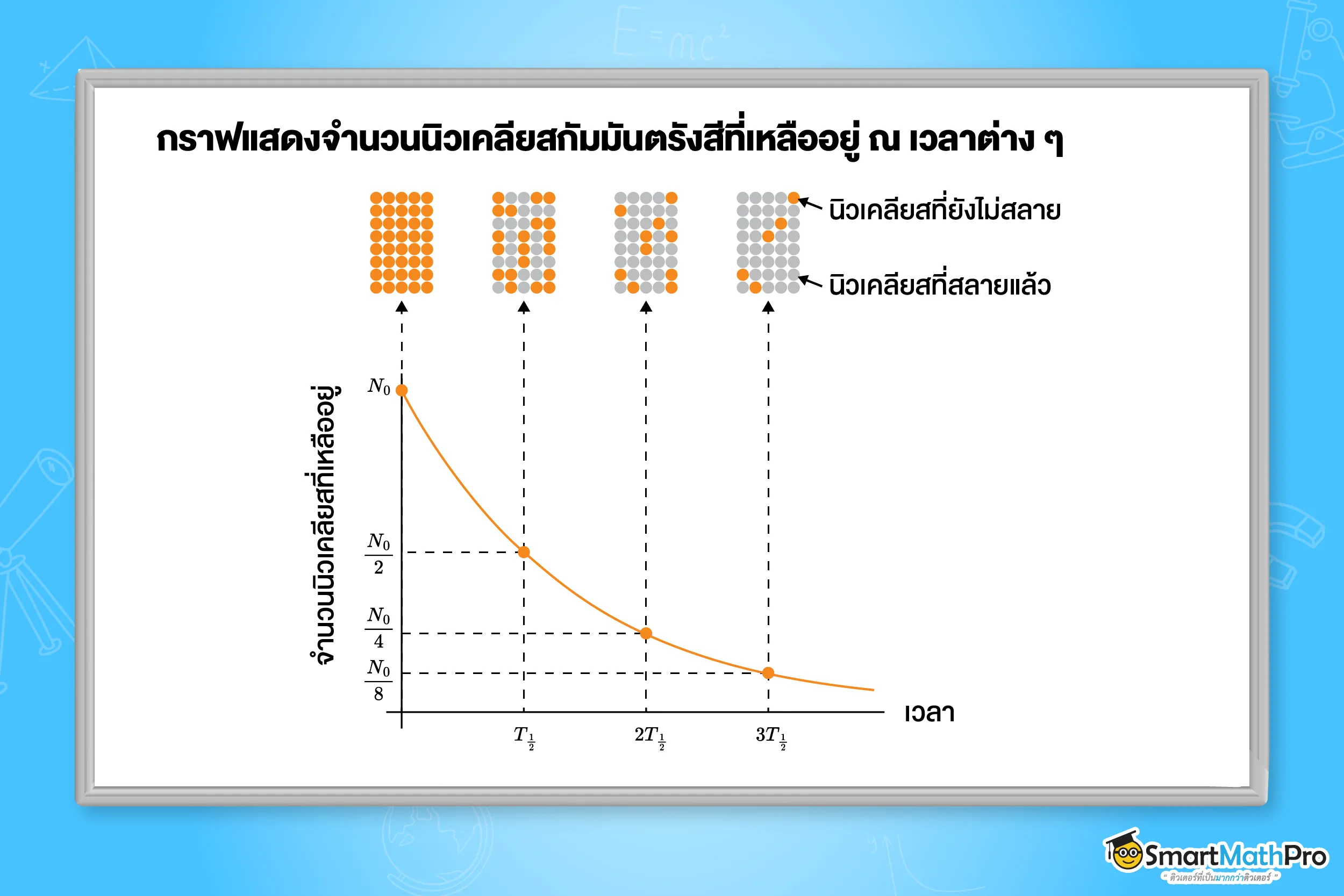
เมื่อเวลาผ่านไปเป็นจำนวนเท่า $2^n$ ของครึ่งชีวิต (โดยที่ $t=nT_{1/2}$ ) ปริมาณที่เหลืออยู่จะลดลงตามสัดส่วน $2^n$

จำนวนนิวเคลียสที่เหลืออยู่ $(N)$
$N=\frac{N_0}{2^n}=\frac{N_0}{2^{t/T}}$
กัมมันตภาพที่เหลืออยู่ $(A)$
$A=\frac{A_0}{2^n}=\frac{A_0}{2^{t/T}}$
มวลที่เหลืออยู่ $(m)$
$m=\frac{m_0}{2^n}=\frac{m_0}{2^{t/T}}$

โดย $T$ คือ ครึ่งชีวิต ${(T}_{1/2})$

ตัวอย่างโจทย์เกี่ยวกับ half-life

โบราณคดีพบซากเรือไม้โบราณที่มีปริมาณคาร์บอน $-14$ เหลืออยู่เพียง $12.5\%$ ของปริมาณที่มีอยู่ในไม้ปัจจุบัน
ถ้าคาร์บอน $-14$ มีครึ่งชีวิต $5,730$ ปี เรือลำนี้มีอายุประมาณกี่ปี

วิธีทำ
พิจารณาสัดส่วนที่ลดลง

เริ่มต้น $100\%$
ผ่านไป $1$ รอบ เหลือ $50\%$
ผ่านไป $2$ รอบ เหลือ $25\%$
ผ่านไป $3$ รอบ เหลือ $12.5\%$

ดังนั้น $n=3$ รอบ $({3T}_{1/2})$

หาอายุเรือ

จากสมการ $t=nT_{1/2}$
แทนค่า $t=3\times5,730$
$t=17,190$
ตอบ เรือลำนี้มีอายุประมาณ $17,190$ ปี

ปฏิกิริยานิวเคลียร์และพลังงานนิวเคลียร์

ปฏิกิริยานิวเคลียร์ (nuclear reaction) คือ กระบวนการที่นิวเคลียสมีการเปลี่ยนแปลงองค์ประกอบภายในเมื่อได้รับการกระตุ้นปฏิกิริยานี้อาจเกิดขึ้นในรูปแบบการสลายตัวของนิวเคลียสกัมมันตรังสี หรือการยิงอนุภาคพลังงานสูงเข้าชนนิวเคลียสเพื่อกระตุ้นให้เกิดการเปลี่ยนแปลงภายใน

สมการปฏิกิริยานิวเคลียร์

ในการเขียนสัญลักษณ์ของปฏิกิริยานิวเคลียร์ เมื่อพิจารณานิวเคลียสของธาตุตั้งต้น $X$ ถูกยิงด้วยอนุภาค $a$ แล้วเกิดนิวเคลียสของธาตุใหม่ $Y$ พร้อมกับปล่อยอนุภาค $b$ ออกมา สามารถเขียนแทนด้วยสมการได้ดังนี้

สมการแบบเต็ม

$^{A}_{Z}\mathrm{X}+a\rightarrow^{A^{\prime}}_{Z^{\prime}}\mathrm{Y}+b$

สมการรูปแบบย่อ

$X\left(a,b\right)Y$

โดย $X$ คือ นิวเคลียสเป้าหมาย
$a$ คือ อนุภาคที่ใช้ยิง
$Y$ คือ นิวเคลียสใหม่ที่เกิดขึ้น
$b$ คือ อนุภาคที่ถูกปล่อยออกมา

ในปฏิกิริยาเคมีทั่วไป จำนวนโปรตอนและนิวตรอนภายในนิวเคลียสจะไม่มีการเปลี่ยนแปลง แต่สำหรับปฏิกิริยานิวเคลียร์ ผลรวมมวลของอนุภาคหลังเกิดปฏิกิริยาจะมีค่าน้อยกว่าผลรวมมวลของอนุภาคก่อนเกิดปฏิกิริยาเสมอ มวลส่วนที่หายไปจะถูกเปลี่ยนรูปไปเป็นพลังงานมหาศาลที่เรียกว่า พลังงานนิวเคลียร์ (Nuclear Energy) ตามทฤษฎีความสัมพันธ์ระหว่างมวลและพลังงานที่อัลเบิร์ต ไอน์สไตน์เสนอไว้ ดังสมการ

$E=(\Delta m)c^{2}$

โดย $E$ คือ พลังงานนิวเคลียร์ที่ปล่อยออกมาจากปฏิกิริยา
$\Delta m$ คือ ผลต่างระหว่างมวลก่อนกับหลังการเกิดปฏิกิริยา
$c$ คือ อัตราเร็วของแสงในสุญญากาศ

ปฏิกิริยานิวเคลียร์ฟิชชัน

ฟิชชัน (fission) คือ ปฏิกิริยานิวเคลียร์ที่นิวเคลียสของธาตุที่มีมวลมากแตกออกเป็นนิวเคลียสที่มีมวลน้อยกว่า

เกิดจากการยิงนิวตรอนเข้าไปในนิวเคลียสของธาตุที่มีมวลมาก เช่น ยูเรเนียม $-235$ ทำให้นิวเคลียสอยู่ในสภาวะไม่เสถียรและแตกตัวออกเป็นนิวเคลียสที่มีมวลน้อยกว่าหลายส่วน พร้อมกับปล่อยนิวตรอนอิสระเพิ่มเติมและพลังงานจำนวนมากออกมา ดังภาพ

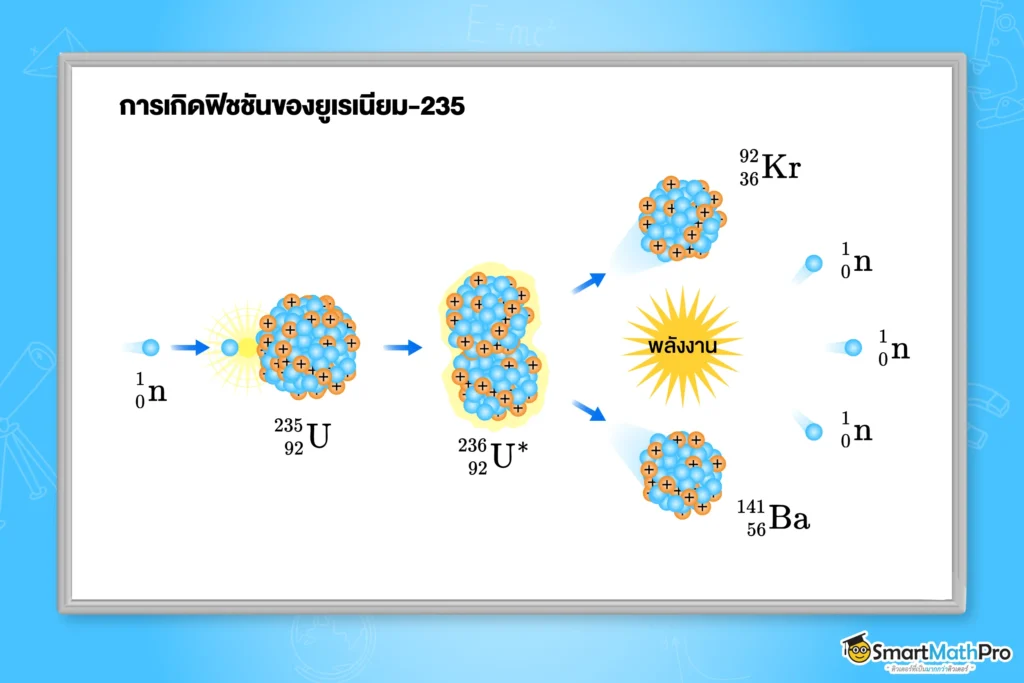
นิวตรอนอิสระที่เกิดขึ้นจากกระบวนการฟิชชันสามารถไปกระตุ้นให้นิวเคลียสอื่นเกิดฟิชชันต่อไปได้ ส่งผลให้เกิด ปฏิกิริยาลูกโซ่ (chain reaction) และมีการปลดปล่อยพลังงานนิวเคลียร์ออกมาในปริมาณมหาศาล ดังภาพ ซึ่งเป็นหลักการสำคัญของการทำงานของเตาปฏิกรณ์นิวเคลียร์

ปฏิกิริยานิวเคลียร์ฟิวชัน

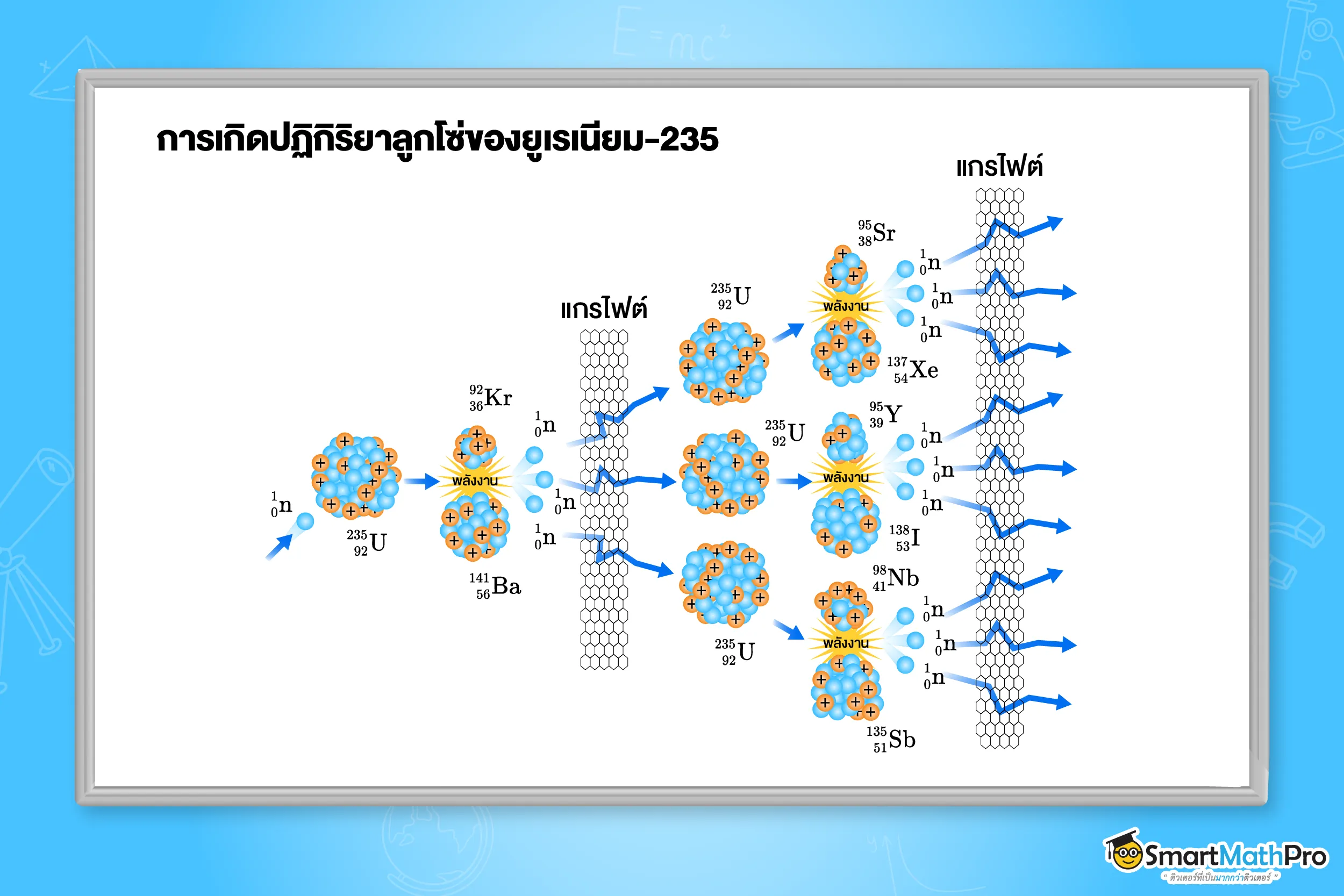
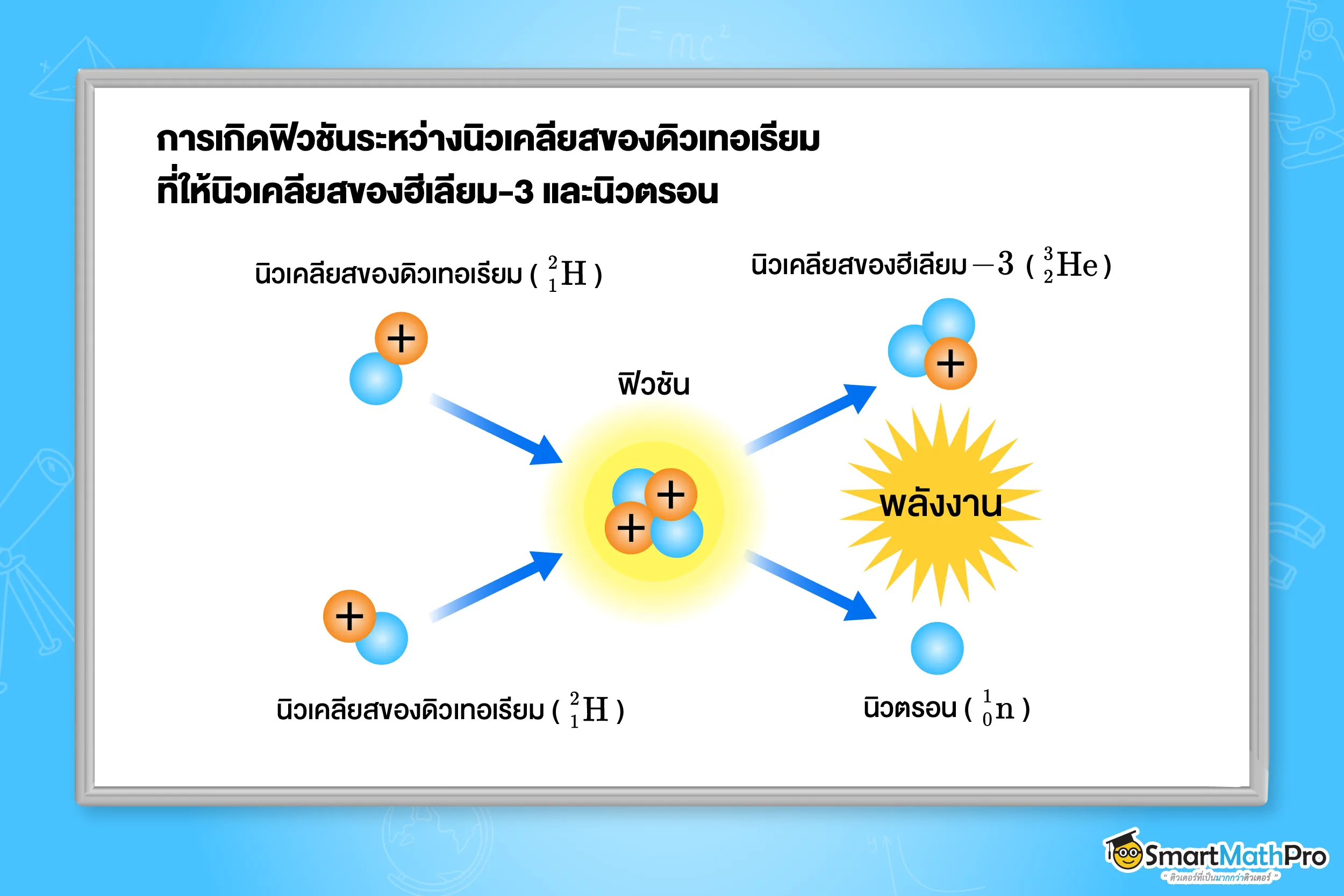
ฟิวชัน (fusion) คือ ปฏิกิริยานิวเคลียร์ที่เกิดจากการหลอมรวมของนิวเคลียสของธาตุเบาหลายชนิดเข้าด้วยกัน จนกลายเป็นนิวเคลียสของธาตุที่มีมวลมากขึ้น เช่น นิวเคลียสของไฮโดรเจนหลอมรวมกันเป็นนิวเคลียสของฮีเลียม พร้อมกับปลดปล่อยพลังงานจำนวนมากออกมา ปฏิกิริยานี้เป็นกระบวนการที่เกิดขึ้นภายในดวงอาทิตย์และดาวฤกษ์ต่าง ๆ และกำลังอยู่ระหว่างการพัฒนาเพื่อนำมาใช้เป็นแหล่งพลังงานสะอาดในอนาคตบนโลก ซึ่งต้องอาศัยสภาวะอุณหภูมิและความดันที่สูงมาก

ตัวอย่าง ปฏิกิริยาฟิวชันที่เกิดขึ้นบนดวงอาทิตย์
$^{1}_{1}\mathrm{H}+{}^{1}_{1}\mathrm{H}\rightarrow{}^{2}_{1}\mathrm{H}+{^{0}_{+1}\mathrm{e}}+0.4\text{ MeV}$

$^{2}_{1}\mathrm{H}+{}^{1}_{1}\mathrm{H}\rightarrow{}^{3}_{2}\mathrm{He}+5.5\text{ MeV}$

$^{3}_{2}\mathrm{H}+{}^{3}_{2}\mathrm{H}\rightarrow{}^{4}_{2}\mathrm{He}+{2^{1}_{1}\mathrm{H}}+12.9\text{ MeV}$

ตัวอย่างโจทย์เกี่ยวกับปฏิกิริยานิวเคลียร์และพลังงานนิวเคลียร์

เมืองแห่งหนึ่งต้องการใช้พลังงานไฟฟ้าทั้งหมด $9\times 10^{12}$ จูลต่อวัน หากโรงไฟฟ้านิวเคลียร์ในเมืองนี้สามารถเปลี่ยนมวลเป็นพลังงานได้อย่างสมบูรณ์ จงหา
ก. ในแต่ละวัน จะต้องมีมวลของเชื้อเพลิงนิวเคลียร์หายไปกี่กรัม เพื่อให้ได้พลังงานตามที่ต้องการ
ข. หากไม่มีโรงไฟฟ้านิวเคลียร์ เมืองนี้จะต้องใช้ถ่านหินวันละกี่ตัน

กำหนดให้ การเผาไหม้ถ่านหิน 1 $1$ กิโลกรัม ให้พลังงาน 3107 $3\times 10^{7}$ จูล

วิธีทำ

หามวลเชื้อเพลิงนิวเคลียร์ที่หายไปต่อวัน
จากสมการ $E=\left( \Delta m \right)c^{2}$
แทนค่า
$9\times10^{12}=\left( \Delta m \right)\left(3\times10^{8} \right)^{2} \\ 9\times10^{12}=\left( \Delta m \right)\left(9\times10^{16} \right) \\ \Delta m=\frac{9\times10^{12}}{9\times10^{16}} \\ \Delta m= 1\times10^{-4}\text{ kg} \\ \Delta m = 0.1\text{ g}$
ดังนั้น มวลของเชื้อเพลิงนิวเคลียร์หายไปเท่ากับ $0.1$ กรัมต่อวัน
หาปริมาณถ่านหินที่ต้องใช้ต่อวัน
พิจารณา พลังงานจากการเผาไหม้ถ่านหินเท่ากับ $3\times 10^{7}$ จูล ต่อมวลถ่านหิน $1$ กิโลกรัม
เทียบกับ พลังงานไฟฟ้าที่ต้องการ $9\times 10^{12}$ จูล ต่อมวลถ่านหิน $x$ กิโลกรัม
จะได้ $x=\frac{9\times10^{12} }{3\times 10^{7}} \\ =3\times10^{5}\text{ kg} \\ =300\text{ ton}$
ดังนั้น เมืองนี้จะต้องใช้ถ่านหินวันละ $300$ ตัน

สูตรฟิสิกส์นิวเคลียร์

ติว A-Level ฟิสิกส์กับ SmartMathPro

พี่ขอแนะนำตัวช่วยอย่าง คอร์สเตรียมสอบมหาลัยฯ ของ SmartMathPro เลยย มีให้เลือกมากมายทั้งสนาม TGAT / TPAT หรือ A-Level และสอนโดยติวเตอร์ที่มีความเชี่ยวชาญในแต่ละวิชาด้วย

โดยในแต่ละคอร์สจะสอนปูพื้นฐานแบบละเอียด อิงตาม Test Blueprint ปีล่าสุด (ใครที่พื้นฐานไม่แน่นก็สามารถเรียนได้) พร้อมพาตะลุยโจทย์แบบไต่ระดับ ตั้งแต่โจทย์ซ้อมมือไปจนถึงข้อสอบเก่าหรือโจทย์ที่ใกล้เคียงกับข้อสอบจริง แถมยังแจกเทคนิคในการทำข้อสอบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้นและช่วยเพิ่มโอกาสในการอัปคะแนนให้อีกด้วย สำหรับน้อง ๆ คนไหนที่สมัครตอนนี้ รับฟรี Unseen Mock Test ชุดพิเศษ และสิทธิพิเศษต่าง ๆ ประจำเดือน ถ้าใครสนใจ คลิก เข้ามาดูรายละเอียดแต่ละคอร์สได้เลยยย

ข้อสอบฟิสิกส์นิวเคลียร์พร้อมเฉลย

เฉลยโจทย์ฟิสิกส์นิวเคลียร์ ข้อที่ 1

ตอบ 4. ฟิวชัน และ $2m_{0}-m_{He}-\frac{E}{932}$

วิธีคิด

หาชนิดของปฏิกิริยานิวเคลียร์
จากสมการปฏิกิริยานิวเคลียร์ พบว่า
สารตั้งต้น คือ นิวเคลียสของออกซิเจน 2 นิวเคลียส ซึ่งเป็นนิวเคลียสเบา
ผลิตภัณฑ์ที่ได้ คือ ซิลิคอน ซึ่งเป็นนิวเคลียสที่มีมวลมากกว่าออกซิเจน และ ฮีเลียม
ลักษณะของปฏิกิริยานี้เป็นการที่ นิวเคลียสเบาหลายตัวรวมกันเกิดเป็นนิวเคลียสที่หนักขึ้น
ดังนั้น ปฏิกิริยานิวเคลียร์ดังกล่าวจึงเป็น “ปฏิกิริยาฟิวชัน”
หามวลของซิลิคอน
จาก $E=(\Delta{m})c^{2}$
จะได้ $E=(\Delta{m})\times 932 \\ E=(m_{\text{ก่อน}}-m_{\text{หลัง}})\times 932 \\ E=(2m_{0}-m_{si}-m_{He})\times 932 \\ \frac{E}{932}=2m_{0}-m_{si}-m_{He} \\ m_{si}=2m_{0}-m_{He}-\frac{E}{932}$
$m_{si}=2m_{0}-m_{He}-\frac{E}{932}$
ดังนั้น มวลหน่วย $u$ ของซิลิคอน เท่ากับ $2m_{0}-m_{He}-\frac{E}{932}$

เฉลยโจทย์ฟิสิกส์นิวเคลียร์ ข้อที่ 2

ตอบ 4. $\frac{6.02\times10^{21}}{2^{5}}\frac{\ln{(2)}}{T}$

วิธีทำ
หาจำนวนนิวเคลียสที่เหลือ
จาก $N=\frac{N_0}{2^{t/T}}$
แทนค่า $N=\frac{0.01A}{2^{5T/T}}$
$N=\frac{(0.01)(6.02\times{10}^{23})}{2^5}$
$N=\frac{6.02\times{10}^{21}}{2^5}$ นิวเคลียส

หากัมมันตภาพ
จาก $A=\lambda N$
แทนค่า $A=\frac{\ln{(2)}}{T}\frac{6.02\times10^{21}}{2^{5}}$

ดังนั้น กัมมันตภาพ (อัตราการแผ่รังสี) จะมีค่า $\frac{6.02\times10^{21}}{2^{5}}\frac{\ln{(2)}}{T}$ นิวเคลียสต่อวินาที