ฟิสิกส์อะตอม ม.6 สรุปพร้อมโจทย์และเฉลยจัดเต็ม

ฟิสิกส์อะตอม เป็นบทที่น้อง ๆ ม.6 อาจคุ้นเคยชื่อนี้กันเป็นอย่างดี และอาจเป็นบทสุดหินของหลาย ๆ คน เนื่องจากมีทฤษฎีให้ต้องเข้าใจและจำเยอะมาก แถมยังเป็นเรื่องที่ออกสอบใน A-Level ฟิสิกส์อีกด้วย สำหรับคนที่งงเรื่องนี้อยู่ ไม่ต้องห่วงน้า วันนี้พี่สรุปเนื้อหาฟิสิกส์อะตอมมาให้ทุกคนอ่านพร้อมโจทย์และเฉลยมาให้ครบแล้ว ไปอ่านกันเลยยย

สนใจหัวข้อไหน ... กดอ่านเลย

ฟิสิกส์อะตอม คืออะไร ?

ตั้งแต่สมัยกรีกโบราณ มนุษย์มีความเชื่อว่าสสารทั้งมวลประกอบด้วยหน่วยที่เล็กที่สุดที่แบ่งแยกไม่ได้ หรือที่เรียกว่า อะตอม อย่างไรก็ตาม กว่าที่แนวคิดนี้จะก้าวข้ามปรัชญาไปสู่การเป็นวิทยาศาสตร์เชิงทดลองได้อย่างชัดเจน ก็ต้องใช้เวลานับศตวรรษ ในช่วงต้นศตวรรษที่ 20 การศึกษาพฤติกรรมของแสงและสสารในระดับที่เล็กที่สุดได้นำไปสู่การถือกำเนิดของฟิสิกส์อะตอม

ฟิสิกส์อะตอม คือ สาขาพื้นฐานที่มุ่งเน้นการทำความเข้าใจโครงสร้างภายในของอะตอมและองค์ประกอบต่าง ๆ ที่ประกอบขึ้นเป็นอะตอม การจัดเรียงตัวของอิเล็กตรอนรอบนิวเคลียส อันตรกิริยาระหว่างอะตอมกับสิ่งอื่น ๆ จนเกิดเป็นทฤษฎีเกี่ยวกับอะตอมต่าง ๆ มากมายในเวลาต่อมา

สมมติฐานของพลังค์และทฤษฎีอะตอมของโบร์

การแผ่คลื่นแม่เหล็กไฟฟ้าของวัตถุดำ

จากการทดลองพบว่า วัตถุทุกชนิด ไม่ว่าจะเป็นของแข็ง ของเหลว หรือแก๊ส หากมีอุณหภูมิสูงกว่าศูนย์องศาสัมบูรณ์ $(0\text{ K})$ จะแผ่คลื่นแม่เหล็กไฟฟ้าออกมาเสมอ โดยคลื่นแม่เหล็กไฟฟ้าที่แผ่ออกมานั้นมีความถี่ต่อเนื่อง เรียกว่า สเปกตรัมต่อเนื่อง และมีความยาวคลื่นสูงสุด $(\lambda_{max})$ ขึ้นกับอุณหภูมิของวัตถุนั้น ๆ ดังรูป

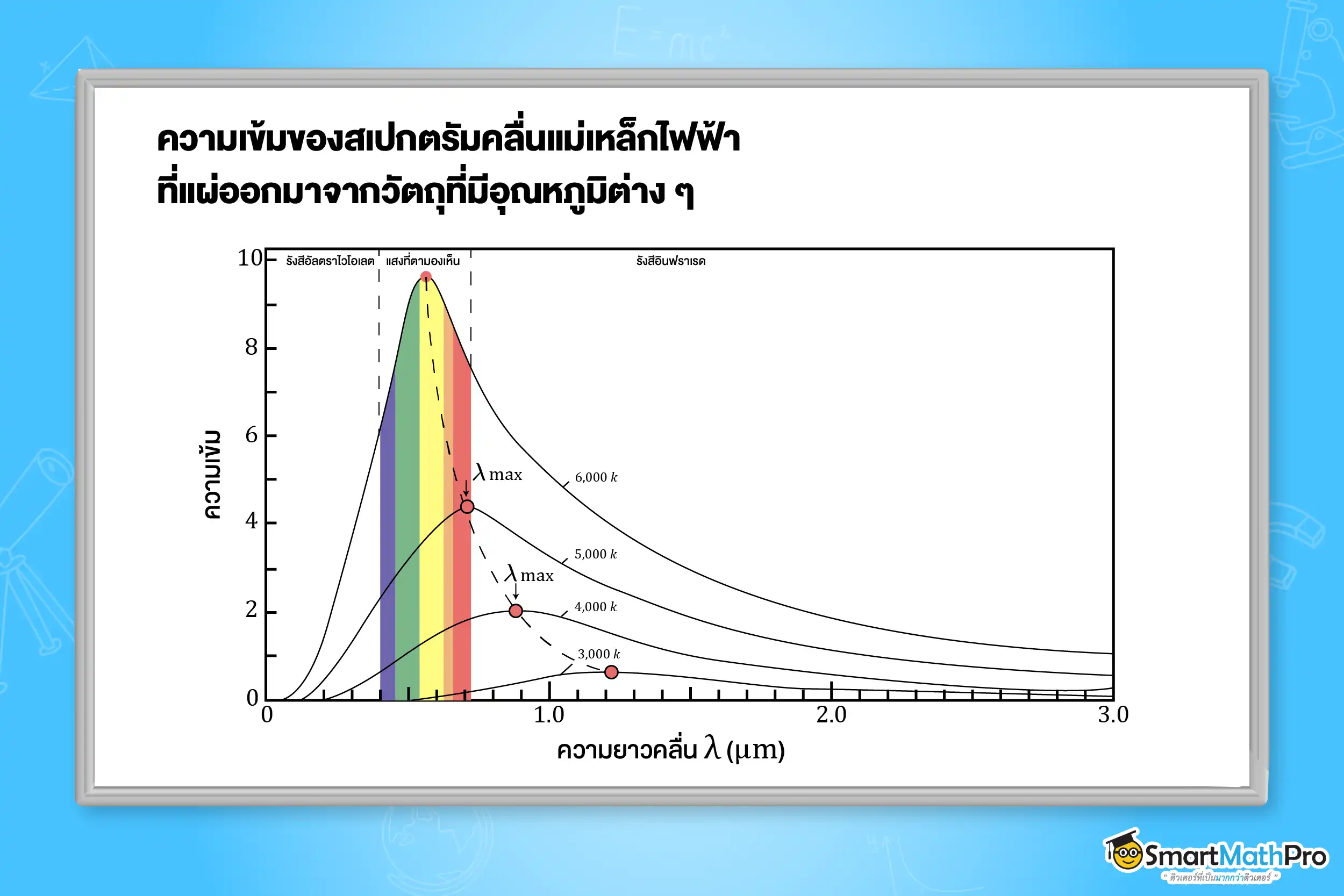
นักวิทยาศาสตร์ได้พยายามหาคำตอบเกี่ยวกับการแผ่ออกมาของคลื่นแม่เหล็กไฟฟ้าที่กระจายออกมาในแต่ละช่วงความยาวคลื่น โดยใช้แนวคิดจากทฤษฎีฟิสิกส์แบบฉบับ (classical physics) พบว่า สมการที่ได้จะตรงกับผลการทดลองในช่วงความยาวคลื่นมากเท่านั้น ส่วนในช่วงความคลื่นสั้น สมการที่ได้กลับไม่ตรงกับผลการทดลองจริง ดังรูป

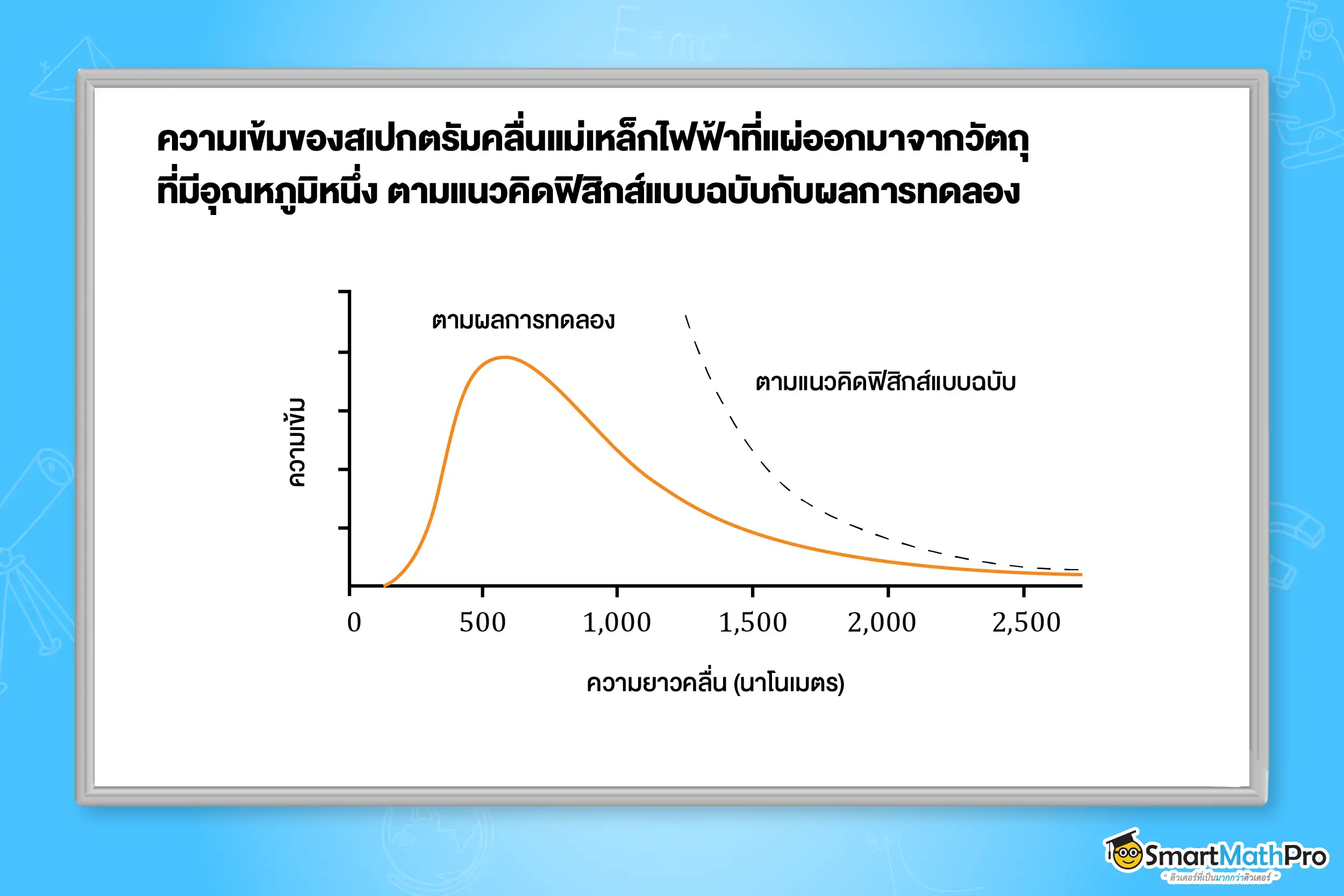
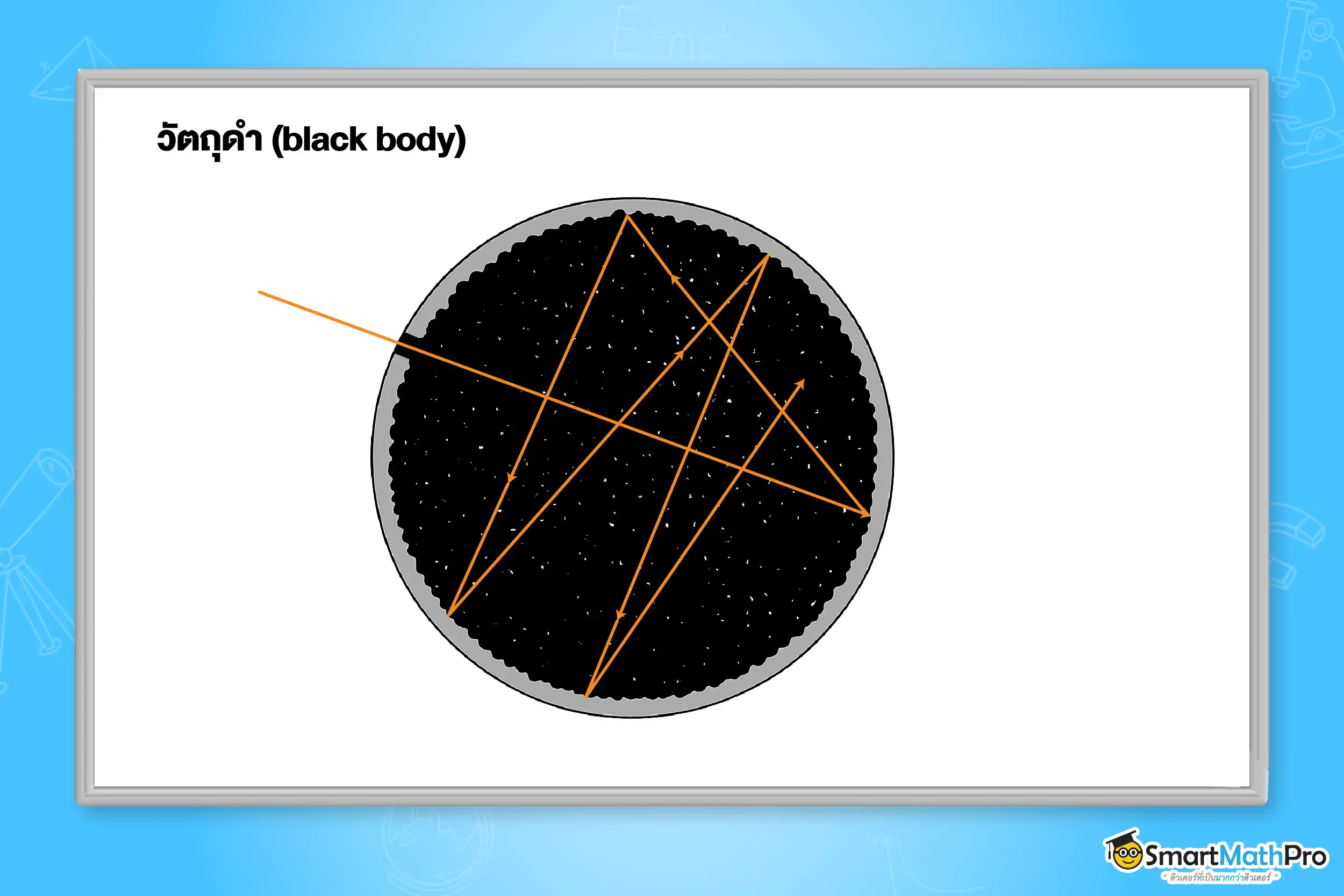
ในปี พ.ศ. 2443 มักซ์ พลังค์ (Max Planck) ได้เสนอแนวคิดปฏิวัติวงการฟิสิกส์เพื่ออธิบายการแผ่รังสีของวัตถุดำ ซึ่ง
ไม่ได้หมายถึงวัตถุสีดำ แต่หมายถึงวัตถุในอุดมคติที่สามารถดูดกลืนรังสีได้หมด และ แผ่รังสีออกมาได้ดีที่สุดในทุกช่วงความถี่ที่อุณหภูมิหนึ่ง ๆ

โดยมีใจความสำคัญ 2 ข้อ

การแผ่และการดูดกลืนพลังงานของวัตถุจะเกิดขึ้นเป็นก้อนหรือชุด ๆ ที่ไม่ต่อเนื่อง (Discrete) เรียกว่า ควอนตัมของพลังงาน (Quantum of Energy)
พลังงานของควอนตัมแต่ละชุดจะมีค่าเป็นจำนวนเต็มเท่าของ $hf$ หรือ $\varepsilon$ เขียนเป็นสมการได้ว่า
$E=n\varepsilon=nhf$

โดย

$E$ คือ พลังงานของคลื่นแม่เหล็กไฟฟ้าที่ดูดกลืน หรือ แผ่ออกมา

$n$ คือ เลขควอนตัม เป็นจำนวนเต็มบวก (เช่น $n=1,\ 2,\ 3,\ \ldots$ ซึ่งแสดงถึงจำนวนโฟตอน)

$h$ คือ ค่าคงตัวของพลังค์ (Planck’s constant) มีค่าประมาณ $6.626\times{10}^{-34}\text{ J}\cdot \text{s}$

ตัวอย่างโจทย์ : การแผ่คลื่นแม่เหล็กไฟฟ้าของวัตถุดำ

จงหาควอนตัมของพลังงานของคลื่นแม่เหล็กไฟฟ้าที่มีความถี่ $8.00\times{10}^{11}\text{ Hz}$

วิธีทำ จาก $\varepsilon=hf$
แทนค่า $h=6.626\times{10}^{-34}\text{ J}\cdot \text{s}$ และ $f=\ 8.00\times{10}^{11}\text{ Hz}$
$\varepsilon=\left(6.626\times{10}^{-34}\right)\left(8.00\times{10}^{11}\ \right)$
$\varepsilon=5.30\times{10}^{-22}\text{ J}$
ตอบ ควอนตัมของพลังงานเท่ากับ $5.30\times{10}^{-22}\text{ J}$

ทฤษฎีอะตอมของโบร์

แบบจำลองอะตอม

แนวคิดเกี่ยวกับโครงสร้างอะตอมได้พัฒนามาอย่างต่อเนื่อง ตามหลักฐานการทดลองที่ค้นพบใหม่ ๆ ในแต่ละยุคสมัย โดยสามารถสรุปการเปลี่ยนแปลงที่สำคัญของแบบจำลองได้ดังนี้

แบบจำลองอะตอมในยุคแรกถูกเสนอโดย จอห์น ดอลตัน โดยระบุว่าอะตอมเป็นเพียง ทรงกลมตัน ที่เล็กที่สุด ไม่ได้สามารถแบ่งแยกและทำลายได้ ซึ่งอะตอมของธาตุชนิดเดียวกันจะมีสมบัติเหมือนกัน แต่จะมีสมบัติต่างจากอะตอมของธาตุอื่น อย่างไรก็ตาม แบบจำลองนี้ไม่สามารถอธิบายการมีอยู่ของอนุภาคที่มีประจุไฟฟ้าภายในอะตอมได้

หลังจากการค้นพบอิเล็กตรอน ทอมสัน ได้เสนอแบบจำลองที่อะตอมเป็นทรงกลมที่เป็นเนื้อเดียวกันของ ประจุบวก ซึ่งมี อิเล็กตรอน กระจายอยู่ในเนื้อทรงกลม เพื่อทำให้อะตอมอยู่ในสภาวะเป็นกลางทางไฟฟ้า

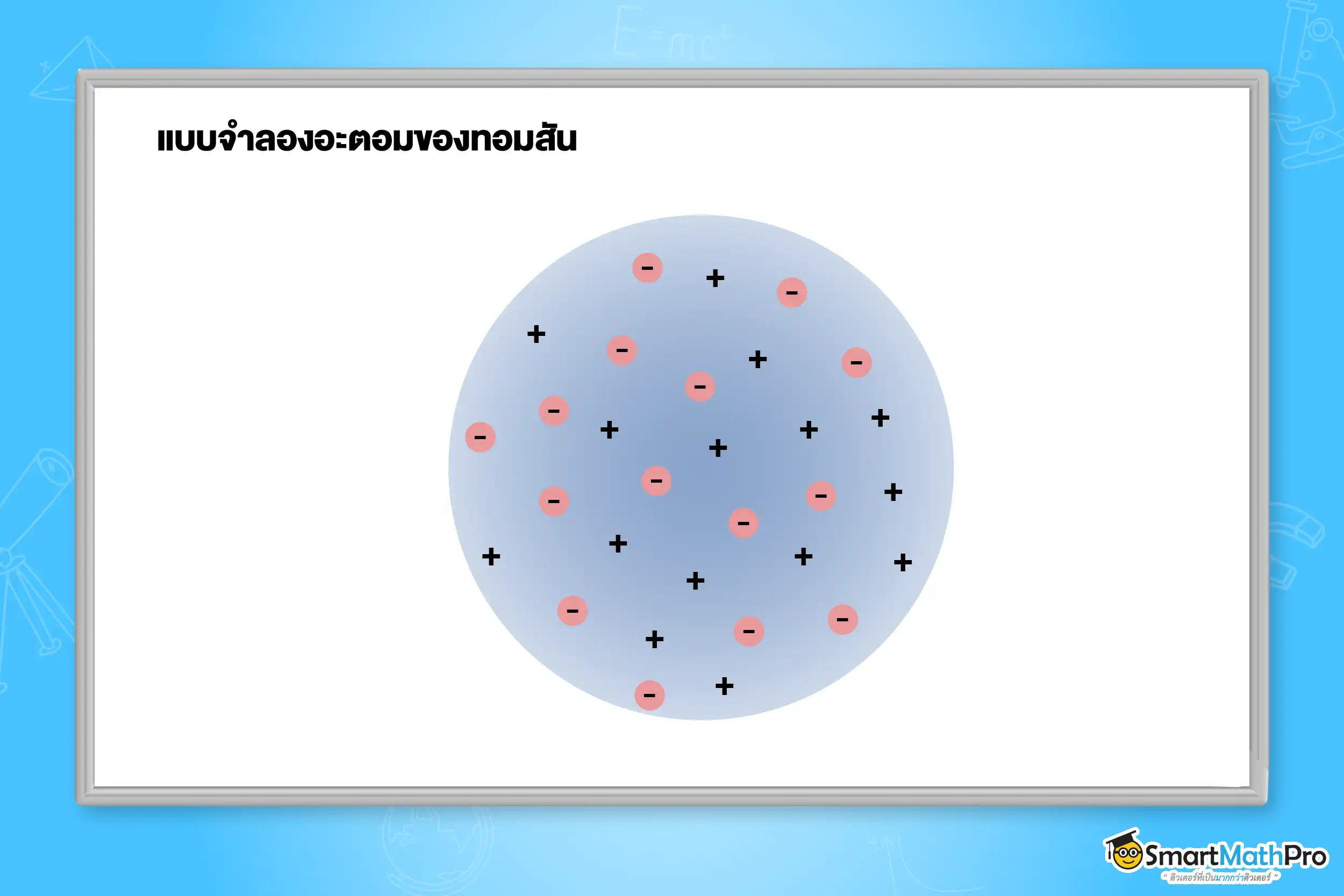
จากการทดลองยิงอนุภาคแอลฟาผ่านแผ่นทองคำบาง เออร์เนสต์ รัทเทอร์ฟอร์ด ได้ค้นพบว่าอะตอมมีพื้นที่ว่างขนาดใหญ่ และประจุบวกส่วนใหญ่อัดแน่นอยู่ในบริเวณเล็ก ๆ ตรงกลางที่เรียกว่า นิวเคลียส จึงนำไปสู่แบบจำลองอะตอมของรัทเทอร์ฟอร์ด ซึ่งมองว่าอะตอมมีนิวเคลียสอยู่ตรงกลางและมีอิเล็กตรอนโคจรอยู่รอบ ๆ อย่างไรก็ตาม แบบจำลองนี้มีข้อบกพร่องตามหลักฟิสิกส์แบบฉบับที่ว่าอิเล็กตรอนควรจะสูญเสียพลังงานและตกลงไปในนิวเคลียส

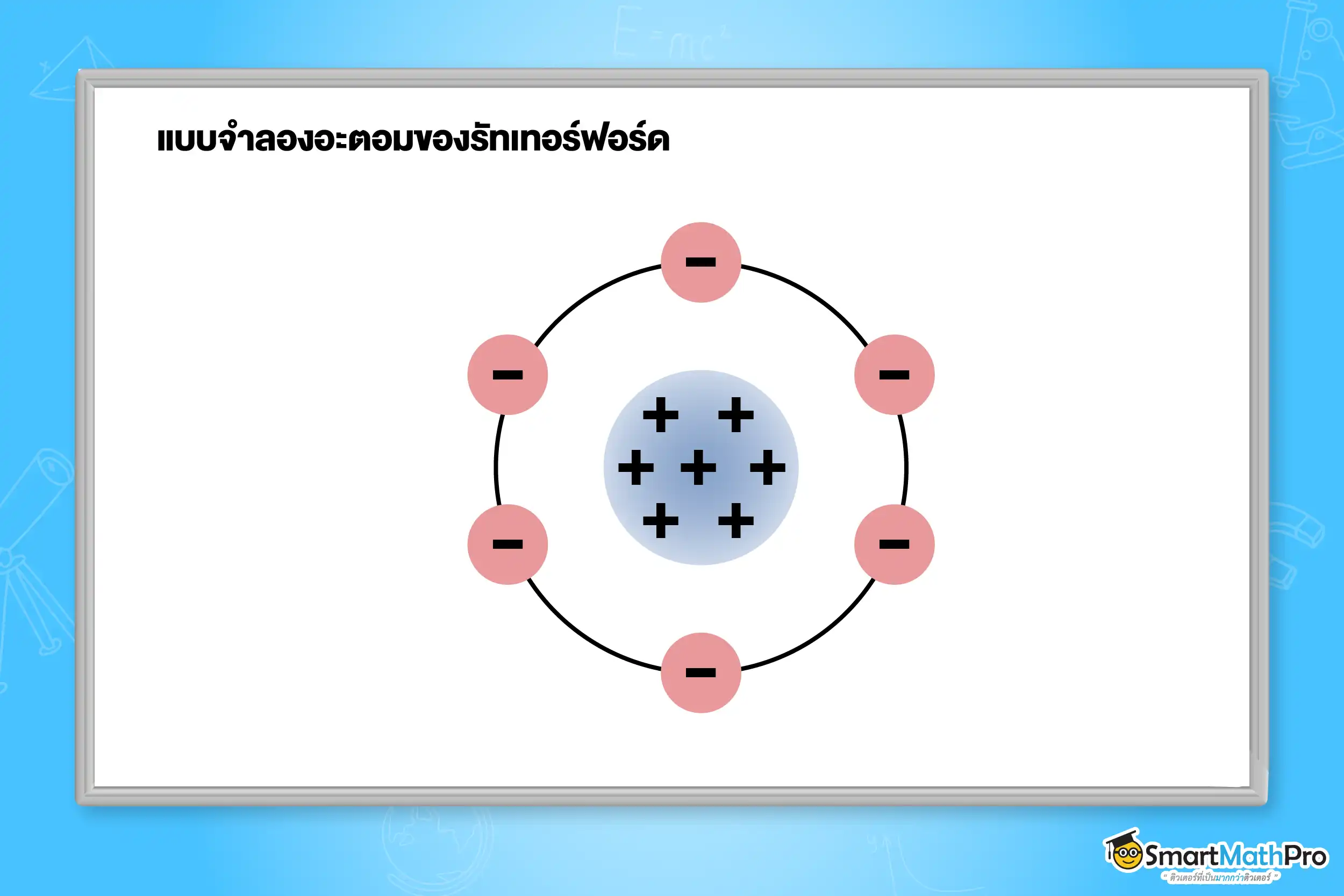
นอกจากปัญหาเรื่องความไม่เสถียรของอิเล็กตรอน ยังมีอีกหนึ่งปัญหา คือ ไม่สามารถอธิบายการแผ่คลื่นแม่เหล็กไฟฟ้าของแก๊สร้อนและเย็นที่แผ่ออกมาเฉพาะบางค่าวามถี่ และยังพบว่าแก๊สแต่ละชนิดจะมีชุดสเปกตรัมที่แตกต่างกัน

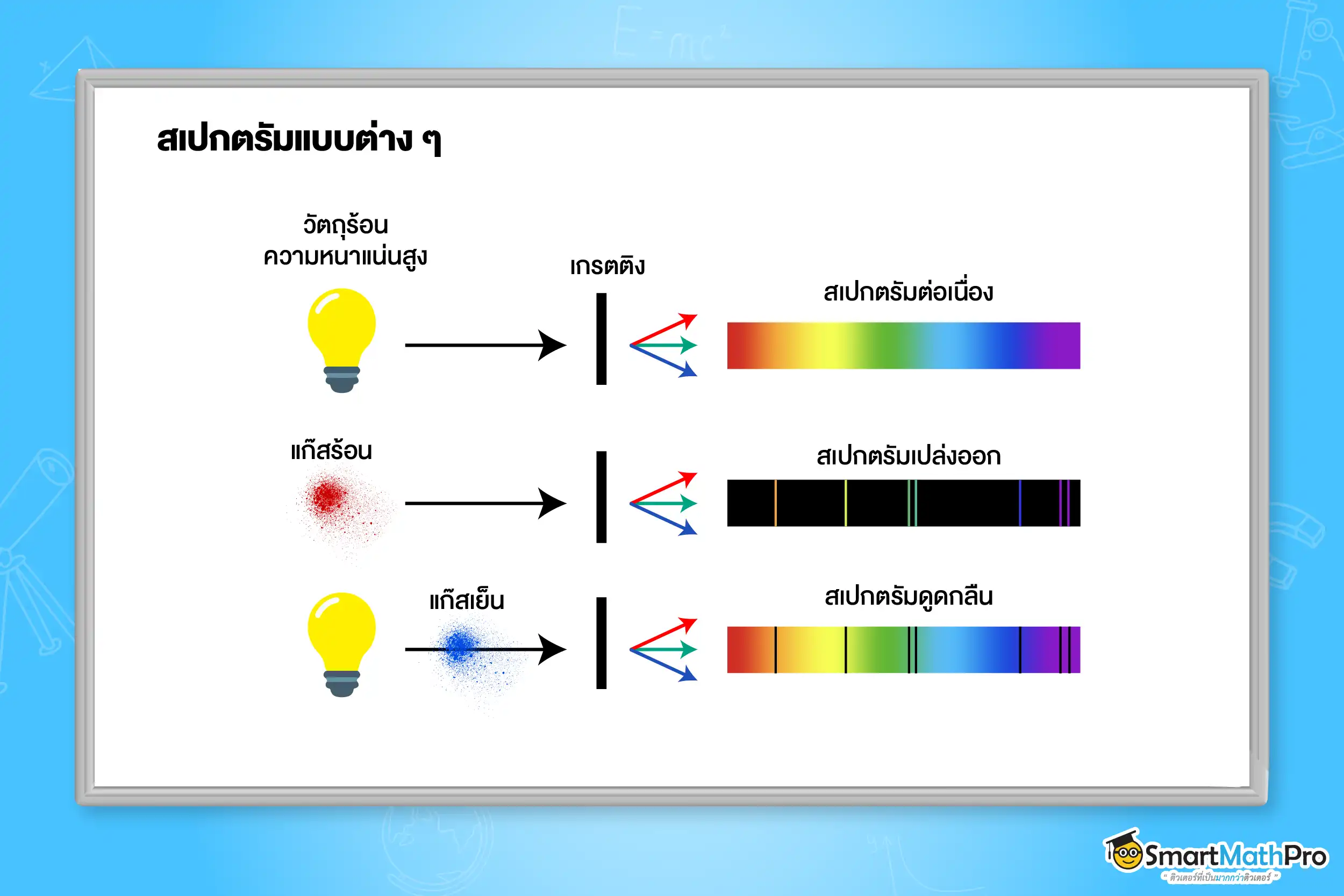
นีลส์ โบร์ ได้เสนอแบบจำลองอะตอมไฮโดรเจนโดยอาศัยแนวคิดของรัทเทอร์ฟอร์ด และแนวคิดของพลังค์ โดยสมมติฐานใหม่ 2 ข้อ

อิเล็กตรอนเคลื่อนที่เป็นวงกลมรอบนิวเคลียสโดยไม่ปล่อยพลังงานในรูปคลื่นแม่เหล็กไฟฟ้าออกมา ในวงโคจรที่เสถียรนี้ อิเล็กตรอนจะมีโมเมนตัมเชิงมุมคงตัว โดยเป็นจำนวนเท่าของ $\bar{h}$

$L=mvr=n\bar{h}$

โดย

$L$ คือ ขนาดโมเมนตัมเชิงมุม

$n$ คือ เลขควอนตัม เป็นจำนวนเต็มบวก

$\bar{h}$ คือ ค่าคงตัว มีค่าเท่ากับ $\frac{h}{2\pi}$

$m$ คือ มวลของอิเล็กตรอน

$r$ คือ รัศมีวงโคจรของอิเล็กตรอน

2. อิเล็กตรอนจะรับหรือปล่อยพลังงานทุกครั้งที่มีการเปลี่ยนวงโคจร โดยพลังงานที่อิเล็กตรอนรับหรือปล่อยจะอยู่ ในรูปคลื่นแม่เหล็กไฟฟ้า ตามสมการ

$\left|E_i-E_f\right|=hf$

โดย

$E_i$ คือ พลังงานของอิเล็กตรอนที่อยู่วงโคจรชั้นนอก

$E_f$ คือ พลังงานของอิเล็กตรอนที่อยู่วงโคจรชั้นใน

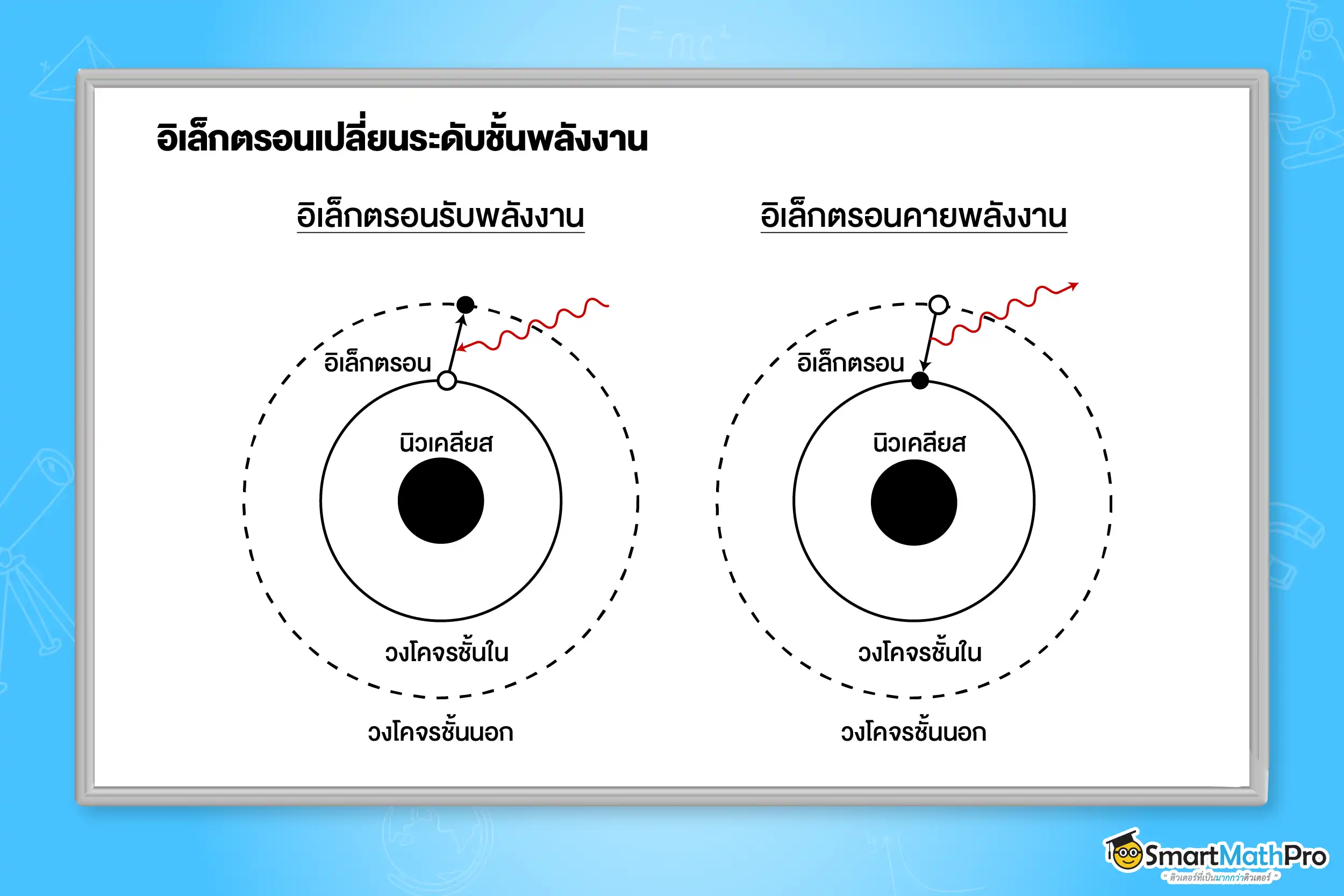
รัศมีวงโคจรของอิเล็กตรอน

$r_n=a_0n^2$

โดย $a_0=0.529\times{10}^{-10}\text{ m}$ เรียกว่า รัศมีโบร์ (Bohr radius)

ระดับพลังงานของอะตอมไฮเดรเจน (hydrogen energy level)

ระดับพลังงานของอิเล็กตรอนในอะตอมไฮโดรเจน สามารถคำนวณได้จากสูตรต่อไปนี้

$E_n=\frac{-13.60}{n^2}\text{ eV}$

โดยที่ $n$ คือ ระดับชั้นพลังงาน

เมื่ออิเล็กตรอนอยู่ในวงโคจรชั้นในสุด $(n=1)$ อะตอมจะมีพลังงานต่ำสุด เรียกว่า สถานะพื้น ซึ่งอะตอมจะมีเสถียรภาพมากที่สุด

เมื่ออิเล็กตรอนได้รับพลังงาน จะทำให้อิเล็กตรอนไปอยู่ในระดับพลังงานที่สูงกว่า เรียกว่า สถานะกระตุ้น อะตอมที่อยู่ในสถานะกระตุ้นพร้อมจะกลับสู่สถานะที่ต่ำกว่าตลอดเวลา และจะปลดปล่อยพลังงานออกมาในรูปคลื่นแม่เหล็กไฟฟ้าเป็นสเปกตรัมสีต่าง ๆ ดังตัวอย่างสเปกตรัมของไฮโดรเจน

ตัวอย่างโจทย์ : ทฤษฎีอะตอมของโบร์

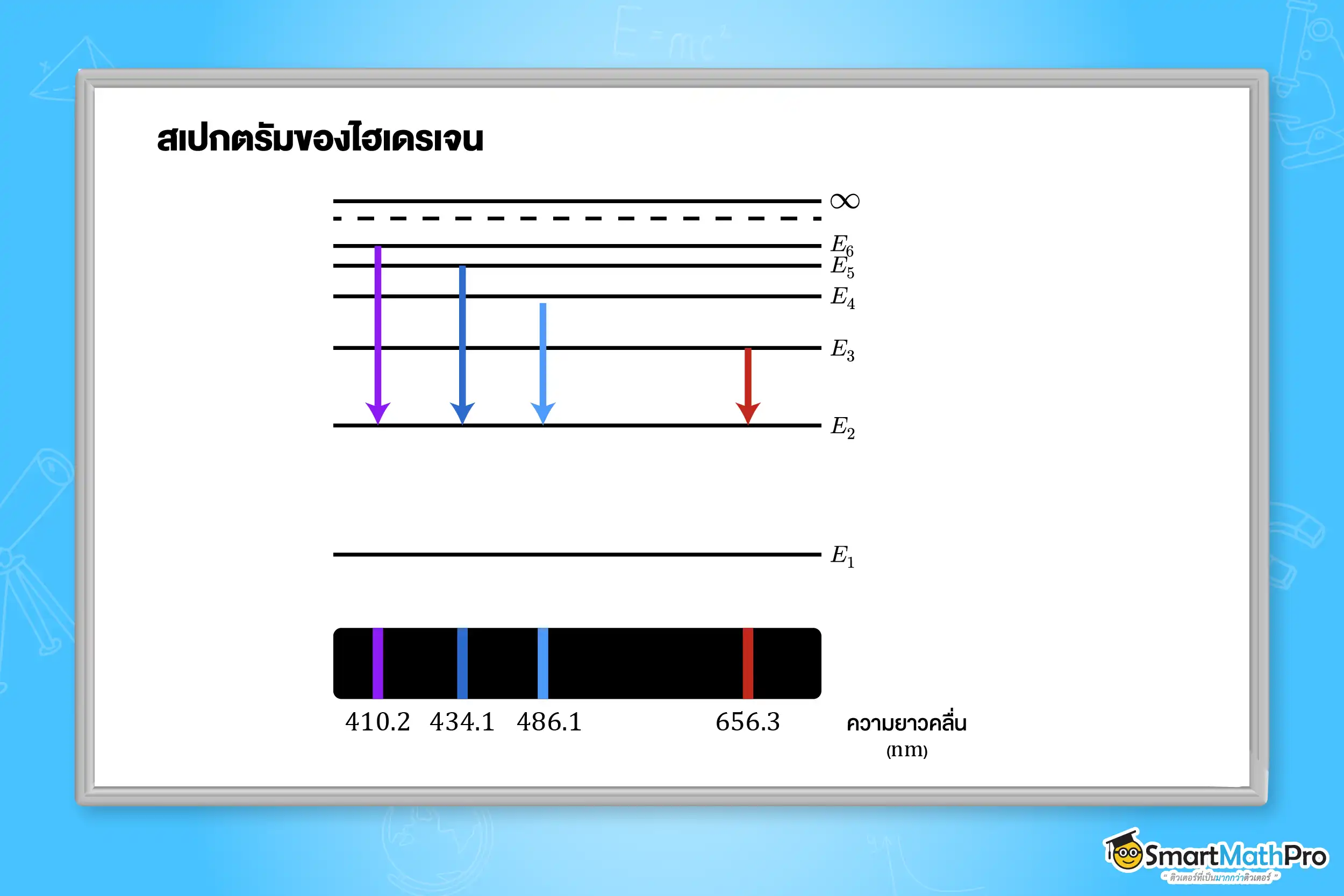
อิเล็กตรอนตัวหนึ่งโคจรรอบนิวเคลียสของอะตอมไฮโดรเจน โดยมี $n=2$ จงหา

ก.รัศมีวงโคจร

ข.ถ้าอิเล็กตรอนกลับสู่สถานะพื้น จะปล่อยคลื่นแม่เหล็กไฟฟ้าที่มีความยาวคลื่นเท่าใด

วิธีทำ

ก. รัศมีวงโคจร

จาก $r_n=a_0n^2$

แทนค่า $r_2={\left(0.529\times{10}^{-10}\right)2}^2$

$r_2=4\left(0.529\times{10}^{-10}\right)$

$r_2=2.116\times{10}^{-10}\text{ m}$

ตอบ รัศมีวงโคจรเท่ากับ $2.116\times{10}^{-10}\text{ m}$

จาก $E_i-E_f=hf$

แทนค่า $E_2-E_1=hf$

$-3.40-(-13.60)=h\frac{C}{\lambda}$

$10.2=\left(6.626\times{10}^{-34}\right)\frac{3\times{10}^8}{\lambda}$

$\lambda=\left(6.626\times{10}^{-34}\right)\frac{3\times{10}^8}{10.2}$

$\lambda=1.95\times{10}^{-26}\text{ m}$

ตอบ ความยาวคลื่นแม่เหล็กไฟฟ้าเท่ากับ $1.95\times{10}^{-26}\text{ m}$

ปรากฏการณ์โฟโตอิเล็กทริก

ปรากฏการณ์โฟโตอิเล็กทริก (photoelectric effect) เป็นปรากฏการณ์ที่อิเล็กตรอนหลุดจากผิวโลหะเมื่อมีแสงที่มีความถี่เหมาะสมมาตกกระทบโดยเรียกอิเล็กตรอนที่หลุดออกมานี้ว่า โฟโตอิเล็กตรอน (photoelectron) และเกิดกระแสโฟโตอิเล็กตรอน (photoelectric current) ถูกค้นพบโดย ไฮน์ริช รูดอล์ฟ แฮทซ์ (Heinrich Rudolf Hertz)

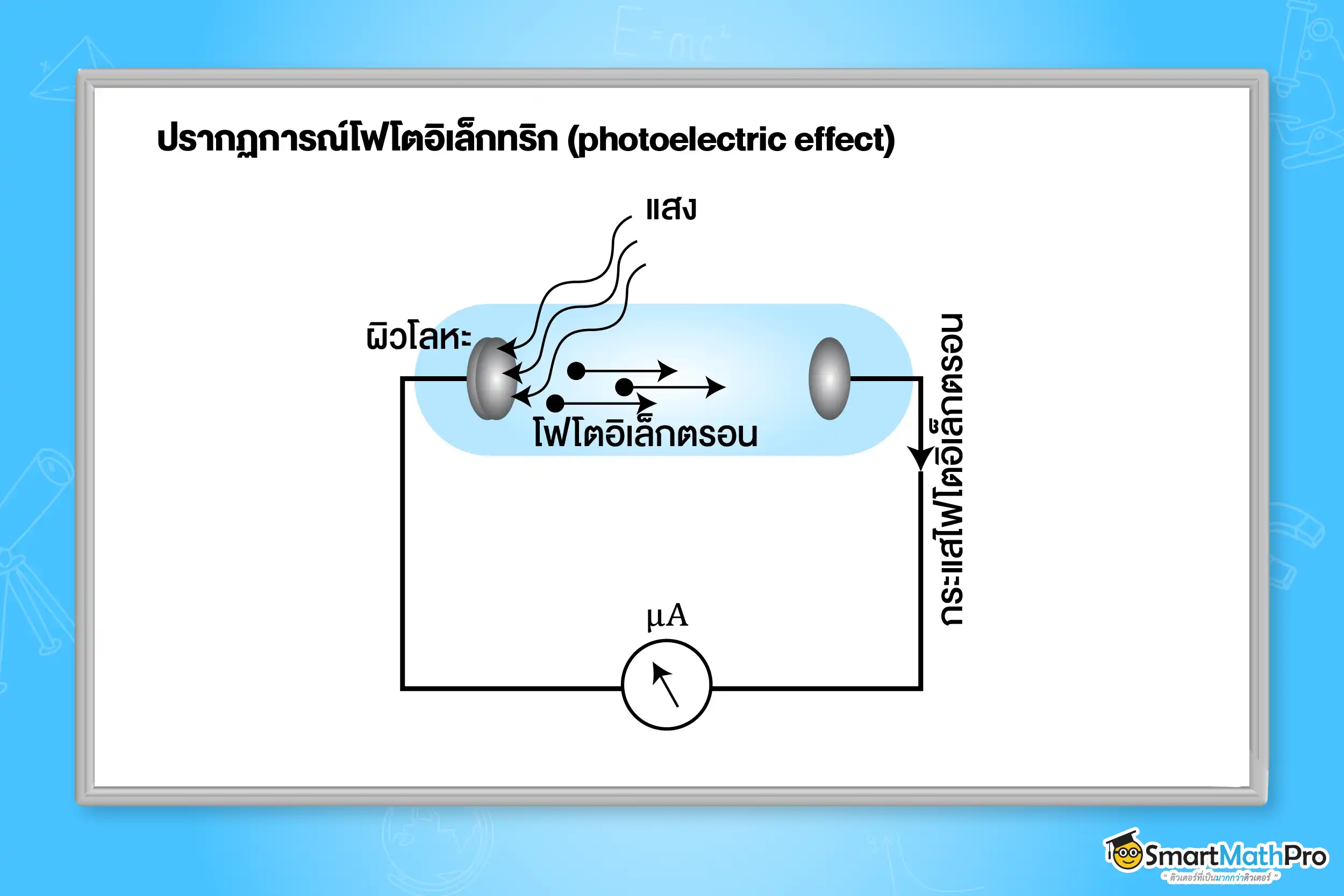
ผลการศึกษาปรากฏการณ์โฟโตอิเล็กทริก สรุปได้ดังนี้

โฟโตอิเล็กตรอนเกิดขึ้นเมื่อแสงที่ตกกระทบกับโลหะมีความถี่สูงถึงค่า ๆ หนึ่ง
จำนวนโฟโตอิเล็กตรอนที่ปลดปล่อยออกมา ขึ้นอยู่กับความเข้มของแสง

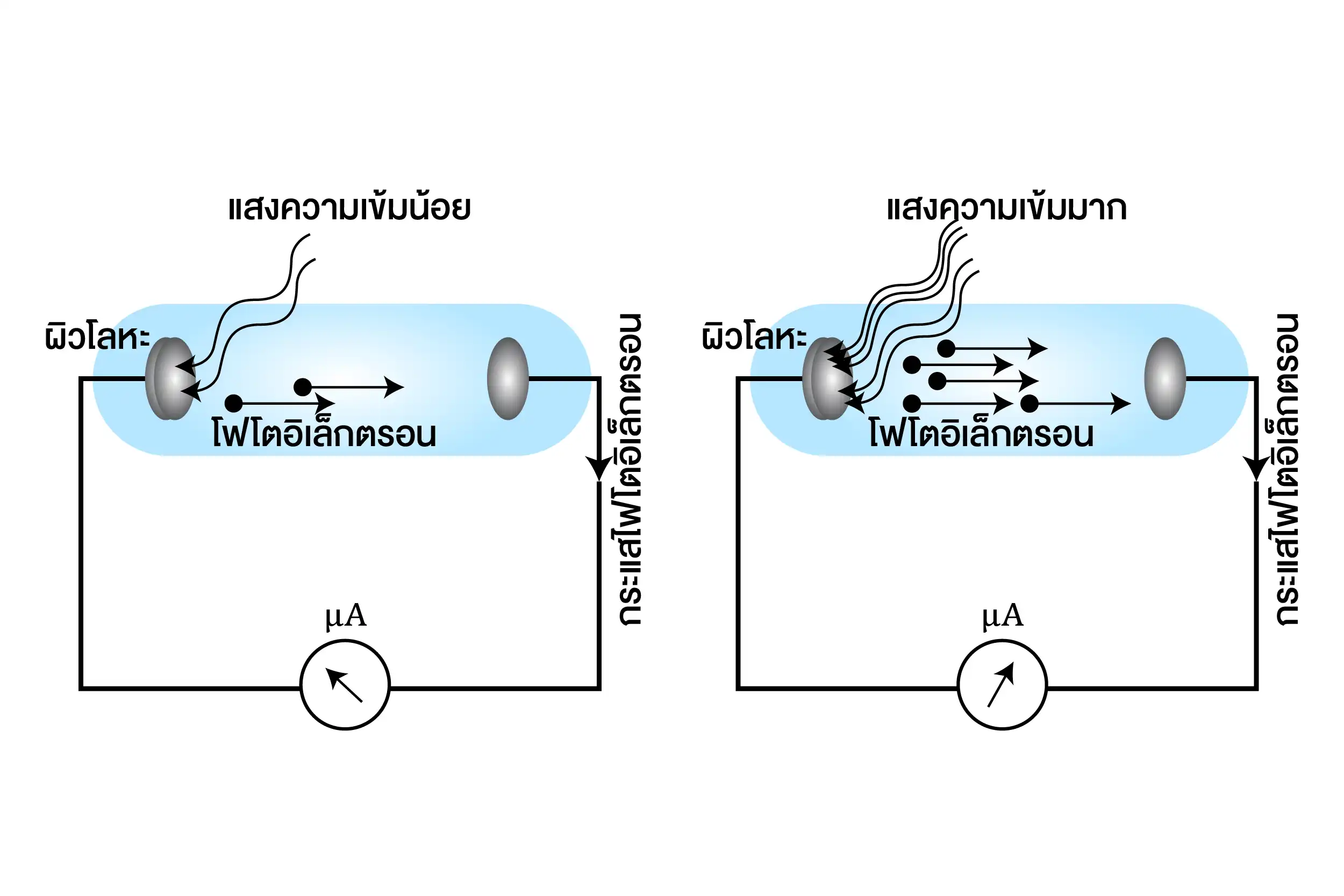
3. พลังงานจลน์สูงสุดของโฟโตอิเล็กตรอนไม่ขึ้นกับความเข้มของแสง แต่ขึ้นกับความถี่ของแสง

ฟังก์ชันงานและพลังงานจลน์สูงสุดของโฟโตอิเล็กตรอน

แอลเบิร์ต ไอน์สไตน์ (Albert Einstein) ได้นำสมมติฐานควอนตัมของพลังค์มาใช้อธิบายผลการทดลองของเฮิรตซ์ โดยเสนอว่าแสงมีสมบัติเป็นอนุภาคที่เรียกว่า โฟตอน (photon) โดยแต่ละโฟตอนมีพลังงานเท่ากับ $hf$ ลำแสงความถี่ $f$ จึงประกอบด้วยโฟตอนจำนวนมาก

เมื่อแสงความถี่ $f$ ตกกระทบบนผิวโลหะ ถ้าความถี่ $f$ ของแสงที่ใช้มีค่ามากกว่าหรือเท่ากับความถี่ค่าหนึ่งที่เรียกว่า ความถี่ขีดเริ่ม (threshold frequency) $f_0$ ก็จะมีโฟโตอิเล็กตรอนหลุดออกมา

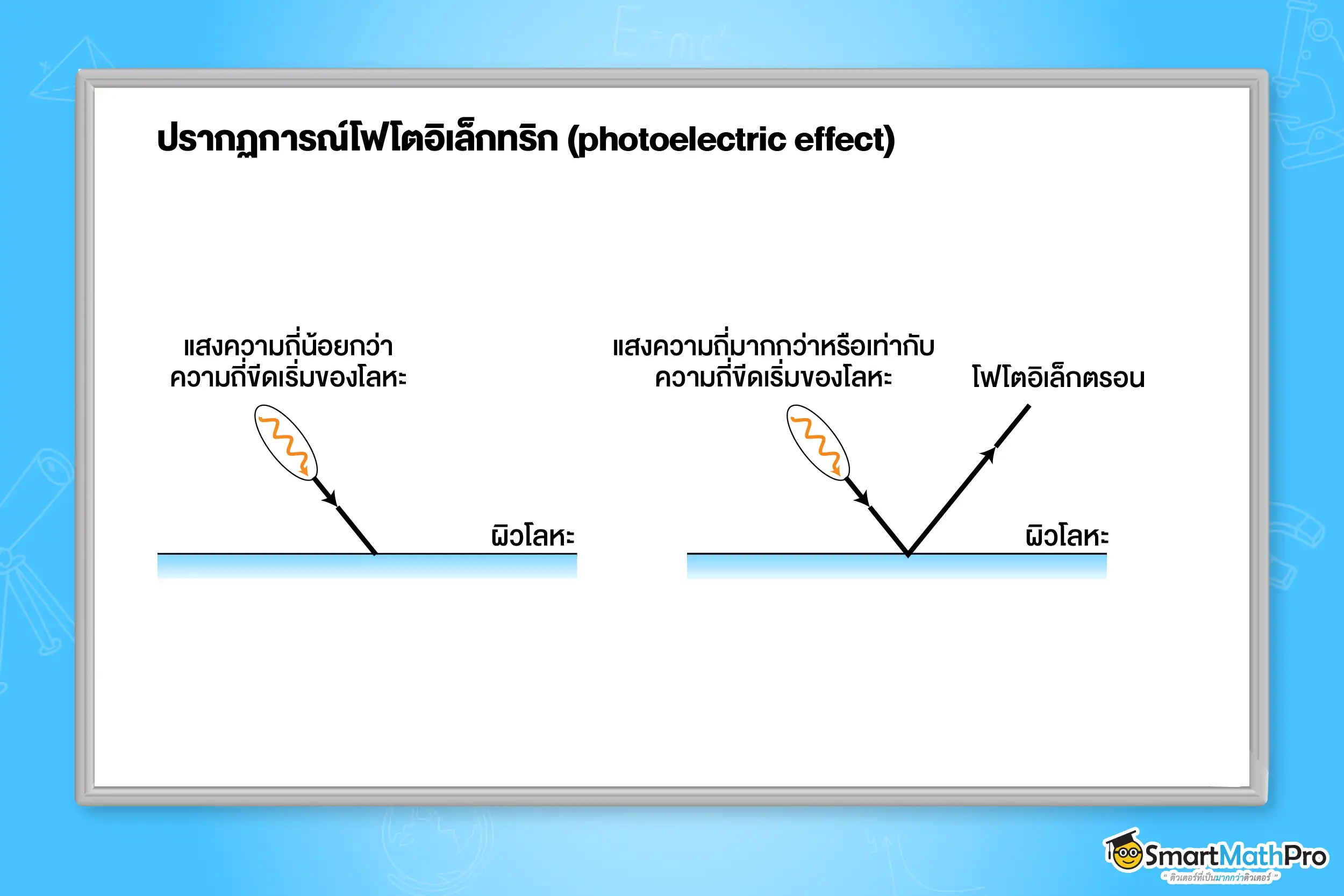
ไอน์สไตน์อธิบายปรากฏการณ์โฟโตอิเล็กทริกนี้ได้โดยอาศัยสมมติฐานควอนตัมของพลังงานของแสงของพลังค์ข้างต้น และกฎการอนุรักษ์พลังงาน ว่าโฟโตอิเล็กตรอนที่หลุดออกมา เกิดจากโฟตอน 1 โฟตอน ชนและถ่ายโอนพลังงานทั้งหมดให้กับอิเล็กตรอน 1 อิเล็กตรอน ตามสมการ

$hf=W+E_{k_{max}}$

โดย

$hf$ คือ พลังงานของโฟตอนที่มีความถี่ $f$ ที่ฉายลงบนผิวโลหะ

$W$ คือ พลังงานที่น้อยที่สุดของโฟตอนที่ทำให้มีโฟโตอิเล็กตรอนได้ มีค่าเท่ากับพลังงานยึดเหนี่ยวอิเล็กตรอนในโลหะ

$E_{k_{max}}$ คือ พลังงานจลน์สูงสุดของโฟโตอิเล็กตรอน

เราสามารถเขียนกราฟความสัมพันธ์ระหว่างพลังงานจลน์สูงสุดของโฟโตอิเล็กตรอนกับความถี่ของโฟตอนที่ตกกระทบผิวโลหะ ซึ่งอยู่ในรูปของสมการเส้นตรง โดยมีความชันของเส้นตรง คือ ค่าคงตัวของพลังค์ คือ $(h)$ และ มีจุดตัดแกนตั้ง คือ $-W$ ดังรูป

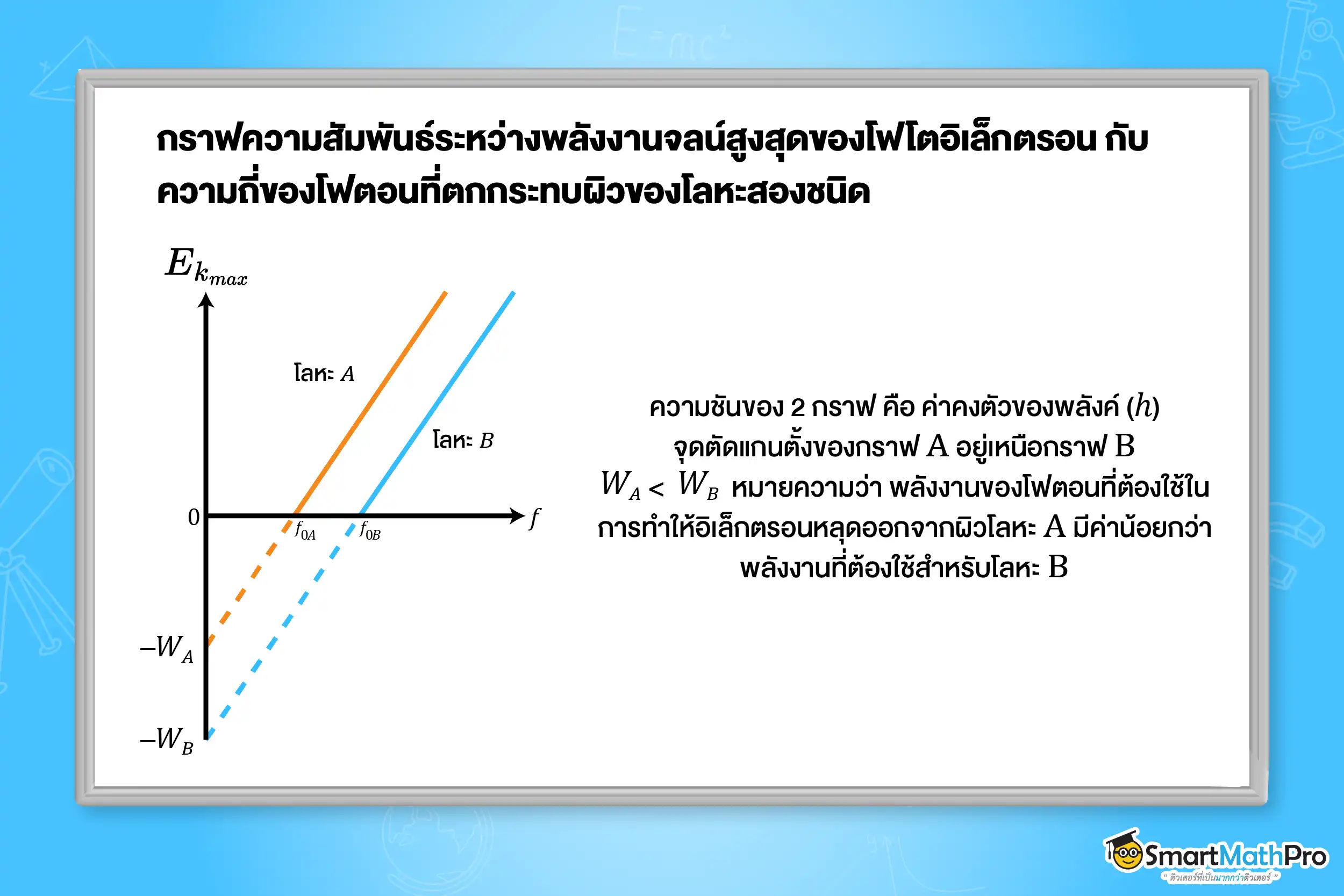
ฟังก์ชันงาน

อิเล็กตรอนถูกยึดเหนี่ยวด้วยพลังงานภายในอะตอมของสสาร การจะดึงอิเล็กตรอนออกจากผิวโลหะต้องใช้พลังงานอย่างน้อยค่าหนึ่ง ซึ่งเรียกว่า “ฟังก์ชันงาน (work function)”

หากพลังงานของโฟตอนที่ตกกระทบมีค่า น้อยกว่า ฟังก์ชันงาน $(hf\lt W)$ หรือ $(f\lt f_0)$ อิเล็กตรอนจะ ไม่หลุดออกมา
หากพลังงานของโฟตอนที่ตกกระทบมีค่า มากกว่าหรือเท่ากับ ฟังก์ชันงาน $(hf\geq\ W)$ หรือ $(f\geq\ f_0)$ อิเล็กตรอนจะ หลุดออกมาจากผิวโลหะได้

เมื่อความถี่ของแสงมีค่าเท่ากับความถี่ขีดเริ่ม $(f=f_0)$ จะเริ่มเกิดโฟโตอิเล็กตรอนพอดี และโฟโตอิเล็กตรอนจะมีพลังงานจลน์สูงสุดเป็นศูนย์ เราสามารถคำนวณฟังก์ชันงาน $(W)$ ของโลหะได้จากสมการ

$W=hf_0$

ซึ่งหมายถึง พลังงานยึดเหนี่ยวของอิเล็กตรอนในโลหะหนึ่ง ๆ นั่นเอง

ตัวอย่าง ฟังก์ชันงานของโลหะบางชนิดแสดงดังตาราง

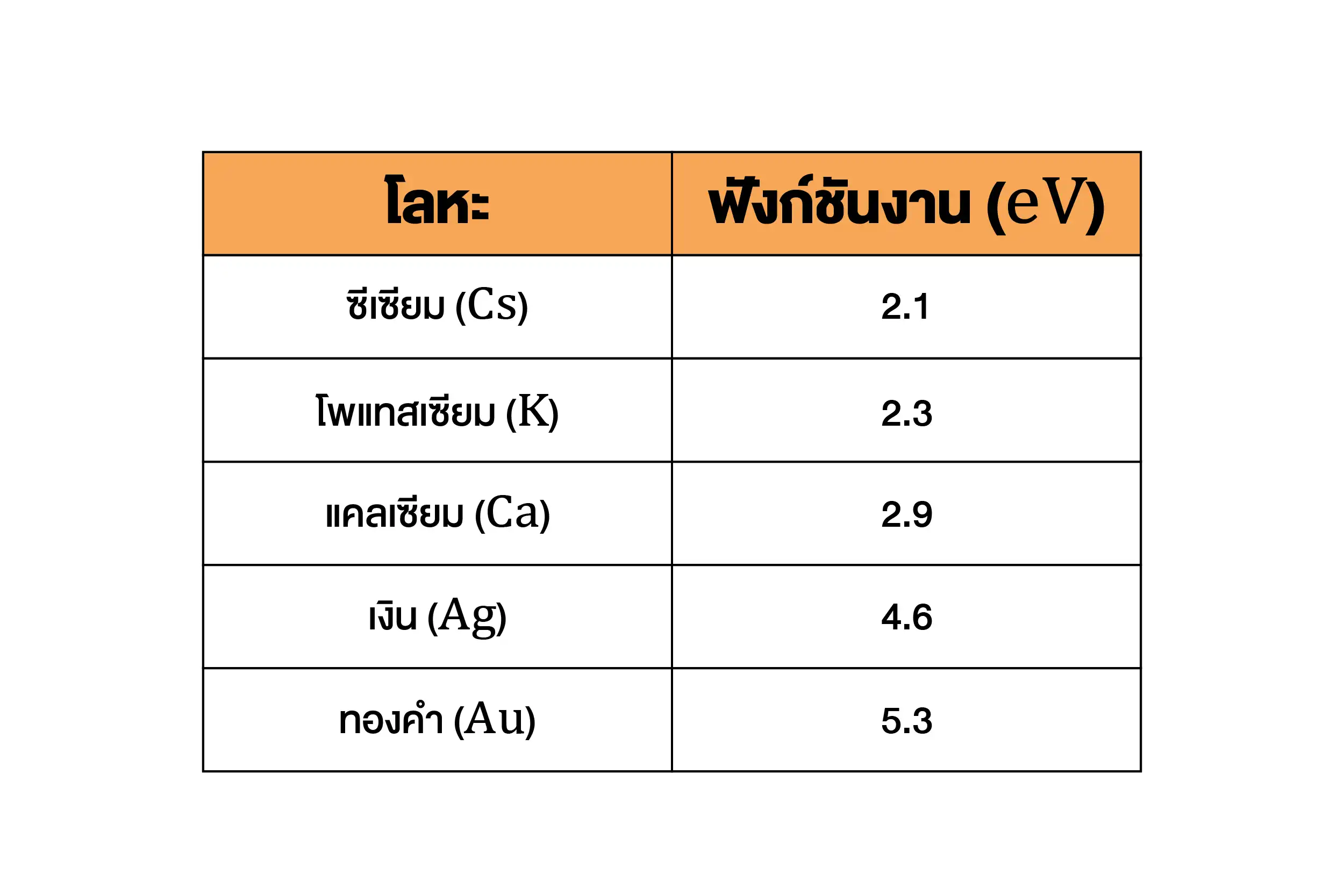
พลังงานจลน์สูงสุดของโฟโตอิเล็กตรอน

เราสามารถหาค่าพลังงานจลน์สูงสุดของโฟโตอิเล็กตรอนจากการทดลองได้โดยการต่อวงจรเพื่อวัด “ศักย์ไฟฟ้าหยุดยั้ง” ซึ่งเป็นศักย์ไฟฟ้าที่มากพอจะหยุดยั้งโฟโตอิเล็กตรอนที่มีพลังงานจลน์สูงสุดไม่ให้ไปถึงแอโนดได้ ดังรูป

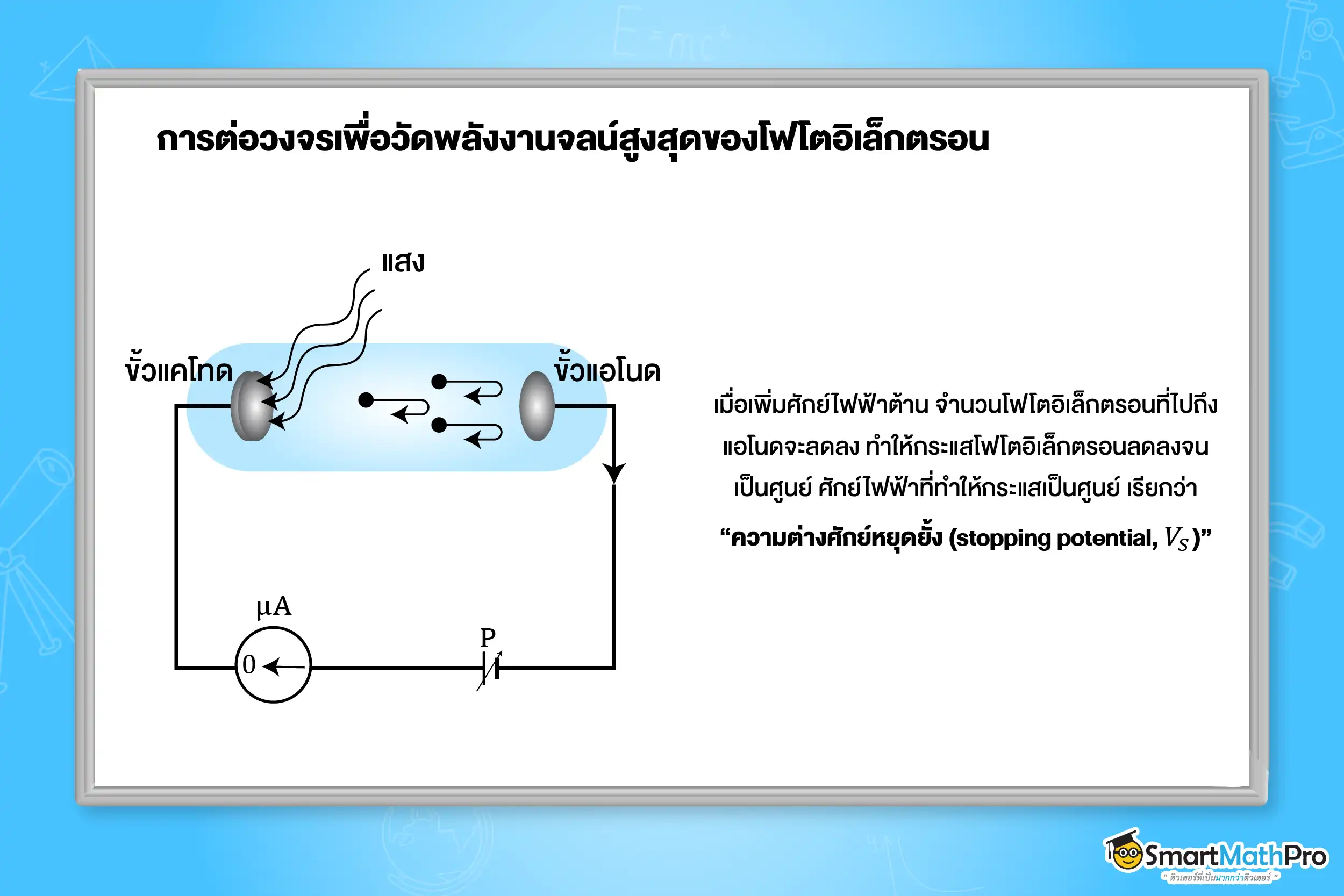
หากโฟโตอิเล็กตรอนมีพลังงานจลน์สูงสุดมากขึ้น จะต้องเพิ่มความต่างศักย์หยุดยั้งให้มากขึ้นด้วย ดังนั้น ความต่างศักย์หยุดยั้งจึงเป็นค่าที่บ่งบอกพลังงานจลน์สูงสุดของโฟโตอิเล็กตรอนได้โดยตรง

เมื่อทำการทดลองโดยใช้แสงที่มีความเข้มเพิ่มขึ้น พบว่า กระแสในวงจรจะเพิ่มขึ้นเนื่องจากมีโฟโตอิเล็กตรอนถูกปล่อยออกมามากขึ้น แต่ค่าศักย์หยุดยั้งจะยังคงเท่าเดิม แสดงว่า พลังงานจลน์สูงสุดของโฟโตอิเล็กตรอนไม่ขึ้นกับความเข้มของแสง แต่ขึ้นกับความถี่ของแสงที่มากระทบ

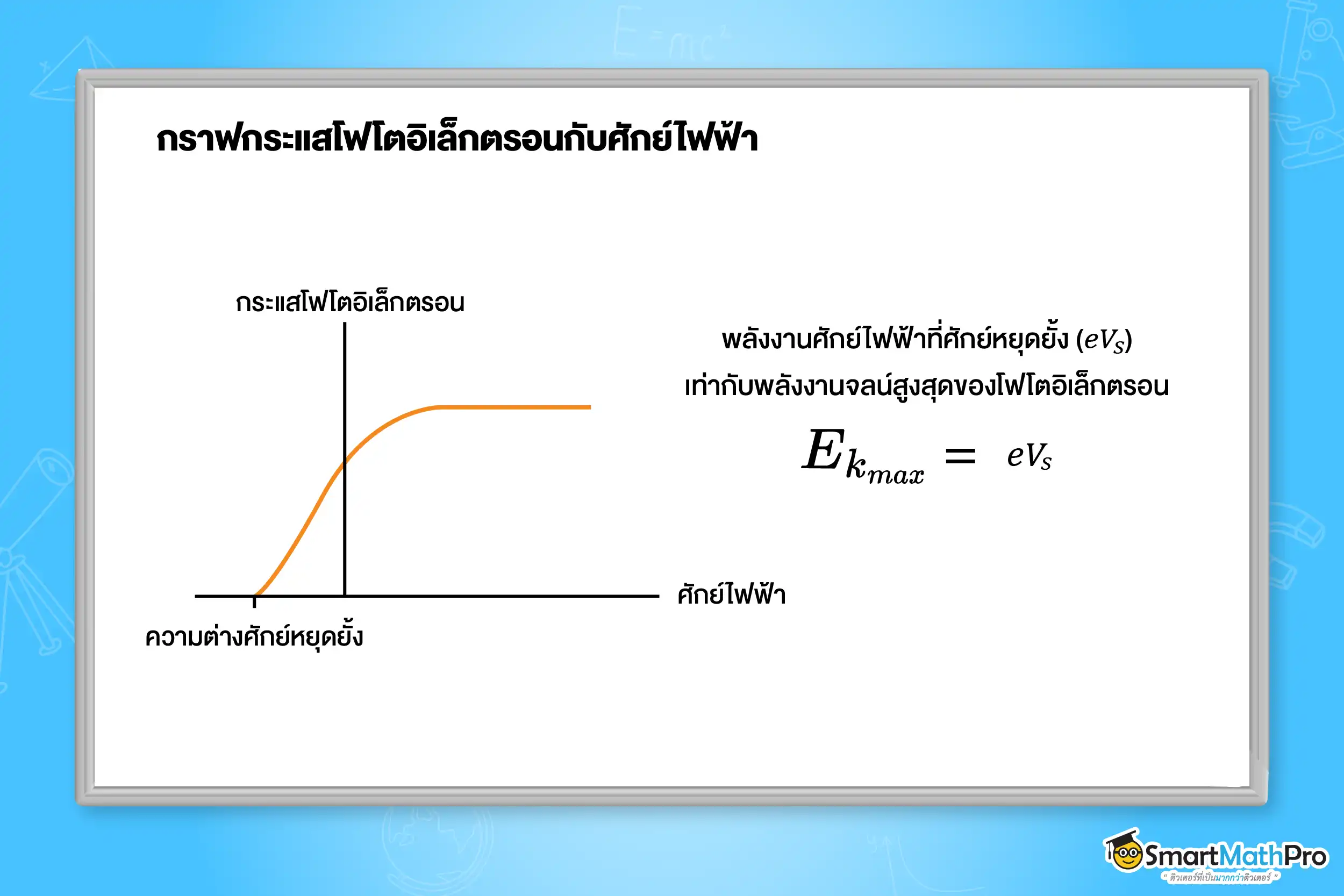
ความสัมพันธ์ระหว่างกระแสไฟฟ้าและความต่างศักย์สามารถแสดงได้ด้วยกราฟ ดังรูป

ตัวอย่างโจทย์ : ปรากฏการณ์โฟโตอิเล็กทริก

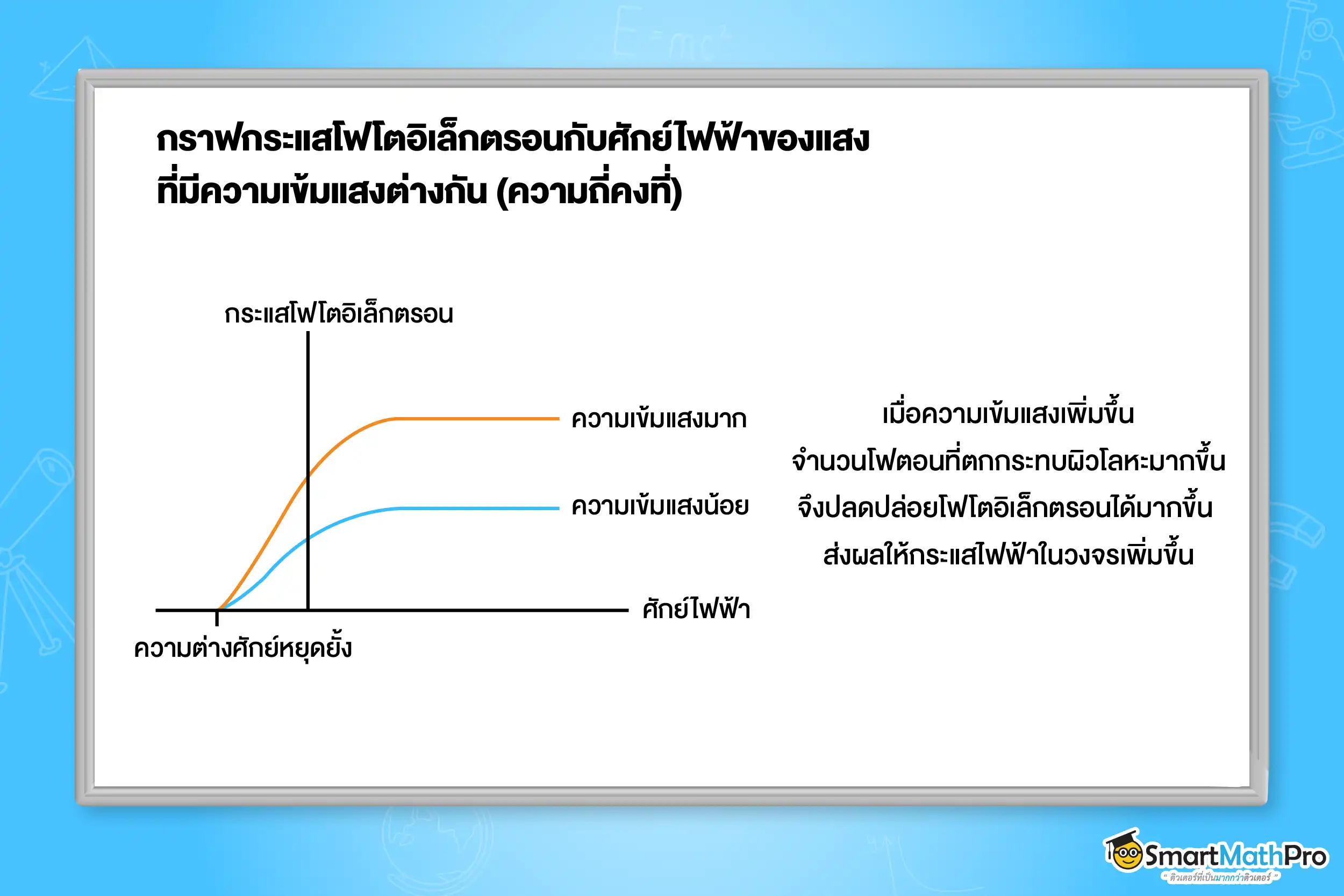
ฉายแสงที่มีความถี่ $1.25\times{10}^{15}\text{ Hz}$ ไปที่ผิวโลหะหนึ่ง ถ้าความถี่ขีดเริ่มมีค่าเป็น $5.10\times{10}^{14}\text{ Hz}$ จงหาฟังก์ชันงานของโลหะและ พลังงานจลน์สูงสุดของโฟโตอิเล็กตรอน ตามลำดับ

1. $2.11\text{ eV},\ 2.75\text{ eV}$

2. $2.11\text{ eV},\ 3.06\text{ eV}$

3. $5.20\text{ eV},\ 2.75\text{ eV}$

4. $5.20\text{ eV},\ 3.06\text{ eV}$

วิธีทำ หาฟังก์ชันงาน จากสมการ $W=hf_0$

$W=\left(6.626\times{10}^{-34}\text{ J}\cdot \text{s}\right)\left(5.10\times{10}^{14}\text{ Hz}\right)$

$W=3.38\times{10}^{-19\ }\text{ J}$

$W=\frac{3.38\times{10}^{-19\ }\text{ J}}{1.60\times{10}^{-19\ }\text{J/eV}}$

$W=2.11\text{ eV}$

ดังนั้น ฟังก์ชันงานของโลหะนั้นมีค่าเท่ากับ $2.11$ อิเล็กตรอนโวลต์

หาพลังงานจลน์สูงสุดของโฟโตอิเล็กตรอน จากสมการ $E_{k_{max}}=hf-W$

$E_{k_{max}}=\left(6.626\times{10}^{-34}\text{ J}\cdot \text{s}\right)\left(1.25\times{10}^{15}\text{ Hz}\right)-(3.38\times{10}^{-19\ }\text{ J})$

$E_{k_{max}}=4.90\times{10}^{-19\ }\text{ J}$

$E_{k_{max}}=\frac{4.90\times{10}^{-19\ }\text{ J}}{1.60\times{10}^{-19\ }\text{J/eV}}$

$E_{k_{max}}=3.06\text{ eV}$

ดังนั้น พลังงานจลน์สูงสุดของโฟโตอิเล็กตรอนมีค่าเท่ากับ $3.06$ อิเล็กตรอนโวลต์

ตอบ ข้อ 2 $2.11\text{ eV},\ 3.06\text{ eV}$

ทวิภาวะของคลื่นและอนุภาค

สมมติฐานของเดอบรอยล์

เดอบรอยล์ได้เสนอแนวคิดว่า “ในเมื่อแสงซึ่งประพฤติตัวเป็นคลื่น สามารถแสดงสมบัติของอนุภาคได้ สิ่งที่เป็นอนุภาค เช่น อิเล็กตรอน ก็น่าจะแสดงสมบัติของคลื่นได้เช่นกัน”

ตามสมมติฐานของเดอบรอยล์ (de Broglie’s hypothesis) อนุภาคที่ประพฤติตัวเป็นคลื่นจะมีความยาวคลื่น $(\lambda)$ ซึ่งเรียกว่า ความยาวคลื่นเดอบรอยล์ (de Broglie wavelength) ซึ่งมีค่าขึ้นกับโมเมนตัม $(P)$ ของอนุภาค ตามสมการ

$\lambda=\frac{h}{P}=\frac{h}{mv}=\frac{h}{\sqrt{2mE_k}}$

โดย $\lambda$ คือ ความยาวคลื่นของอนุภาค

$P$ คือ โมเมนตัมของอนุภาค

$m$ คือ มวลของอนุภาค

$v$ คือ ความเร็วของอนุภาค

$E_k$ คือ พลังงานจลน์ของอนุภาค

เดอ บรอยล์ได้อธิบายสมมติฐานของโบร์ว่า การโคจรของอิเล็กตรอนรอบนิวเคลียสไม่เกิดการแผ่คลื่นแม่เหล็กไฟฟ้าออกมา เนื่องจากอิเล็กตรอนที่เคลื่อนที่รอบนิวเคลียสแสดงสมบัติเป็นคลื่นนิ่งได้ โดยมีความยาวเส้นรอบวงของวงโคจรมีค่าเป็นจำนวนเต็มเท่าของความยาวคลื่นของอิเล็กตรอน ดังรูป

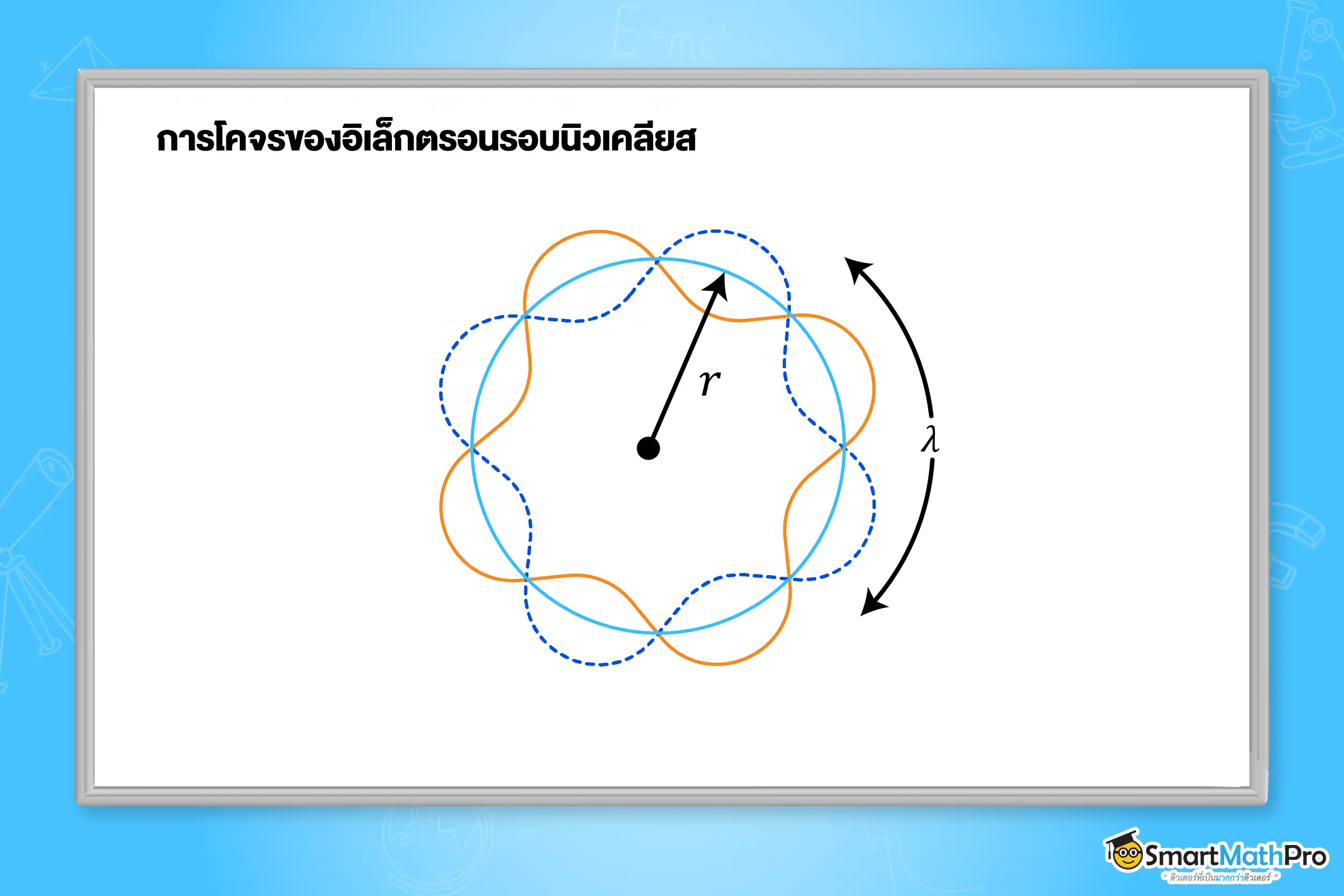
ช่วงความยาวคลื่นที่ทำให้เกิดคลื่นนิ่ง สามารถเขียนความสัมพันธ์ ได้ดังนี้

$2\pi\ r=n\lambda$ เมื่อ $(n=1,\ 2,\ 3,\ \ldots)$

$2\pi\ r=n\left(\frac{h}{mv}\right)$

$mvr=n\left(\frac{h}{2\pi}\right)$

$mvr=n\bar{h}$

โดย

$r$ คือ รัศมีวงโคจรของอิเล็กตรอน

$\lambda$ คือ ความยาวคลื่น

อธิบายสมมติฐานของโบร์ที่ว่า มีวงโคจรบางวงที่อีเล็กตรอนที่เคลื่อนรอบนิวเคลียสโดยไม่มีการแผ่คลื่นแม่เหล็กไฟฟ้า และอิเล็กตรอนจะมีขนาดโมเมนตัมเชิงมุม $L=mvr=n\bar{h}$

ตัวอย่างโจทย์ : ทวิภาวะของคลื่นและอนุภาค

อิเล็กตรอนที่ประพฤติตัวเป็นคลื่นมีความยาวคลื่น $0.20$ นาโนเมตร จะมีโมเมนตัมและพลังงานเท่าใด

วิธีทำ หาโมเมนตัมของอิเล็กตรอน จากสมการ $P=\frac{h}{\lambda}$

$P=\frac{6.626\times{10}^{-34}\text{ J}\cdot \text{s}}{0.20\times{10}^{-9\ }\text{m}}$

$P=3.31\times{10}^{-24\ }\text{kg}\cdot \text{m/s}$

ดังนั้น โมเมนตัมของอิเล็กตรอน มีค่าเท่ากับ $3.31\times{10}^{-24\ }\text{kg}\cdot \text{m/s}$

หาพลังงานของอิเล็กตรอน จากสมการ $E=\frac{P^2}{2m}$

$E=\frac{{(3.31\times{10}^{-24\ }\text{ kg}\cdot \text{m/s}})^2}{2(9.11\times{10}^{-31\ }\text{ kg})}$

$E=6.01\times{10}^{-18\ }\text{ J}$

$E=\frac{6.01\times{10}^{-18\ }\text{ J}}{1.60\times{10}^{-19\ }\text{ J/eV}}$

$E=37.6\text{ eV}$

ดังนั้น พลังงานของอิเล็กตรอนมีค่าเท่ากับ $37.6\text{ eV}$

ตอบ อิเล็กตรอนมีโมเมนตัมและพลังงาน $3.31\times{10}^{-24\ }\text{ kg}\cdot \text{m/s}$ และ $37.6\text{ eV}$ ตามลำดับ

ติว A-Level ฟิสิกส์ กับ SmartMathPro

พี่ขอแนะนำตัวช่วยอย่าง คอร์สเตรียมสอบมหาลัยฯ ของ SmartMathPro เลยย มีให้เลือกมากมายทั้งสนาม TGAT / TPAT หรือ A-Level และสอนโดยติวเตอร์ที่มีความเชี่ยวชาญในแต่ละวิชาด้วย

โดยในแต่ละคอร์สจะสอนปูพื้นฐานแบบละเอียด อิงตาม Test Blueprint ปีล่าสุด (ใครที่พื้นฐานไม่แน่นก็สามารถเรียนได้) พร้อมพาตะลุยโจทย์แบบไต่ระดับ ตั้งแต่โจทย์ซ้อมมือไปจนถึงข้อสอบเก่าหรือโจทย์ที่ใกล้เคียงกับข้อสอบจริง แถมยังแจกเทคนิคในการทำข้อสอบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้นและช่วยเพิ่มโอกาสในการอัปคะแนนให้อีกด้วย สำหรับน้อง ๆ คนไหนที่สมัครตอนนี้ รับฟรี Unseen Mock Test ชุดพิเศษ และสิทธิพิเศษต่าง ๆ ประจำเดือน ถ้าใครสนใจ คลิก เข้ามาดูรายละเอียดแต่ละคอร์สได้เลยยย

ข้อสอบฟิสิกส์อะตอมพร้อมเฉลย

1. จากแบบจำลองอะตอมไฮโดรเจนของโบร์ ถ้ารัศมีการโคจรของอิเล็กตรอนสำหรับสถานะกระตุ้นที่สองของอะตอมไฮโดรเจนเป็น $a$

คำถาม รัศมีการโคจรของอิเล็กตรอนสำหรับสถานะพื้นเป็นเท่าใด [A-Level ฟิสิกส์ ปี 68]

$\frac{3a}{4}$
$\frac{a}{2}$
$\frac{a}{3}$
$\frac{a}{4}$
$\frac{a}{9}$

เฉลยข้อสอบฟิสิกส์อะตอมข้อที่ 1

วิธีทำ จาก $r_n=a_0n^2$
แทนค่า $r_3=a_03^2$ (สถานะกระตุ้นที่สอง, $n=3$ )
$r_3=r_13^2$
$a=r_13^2$
$r_1=\frac{a}{9}$
ตอบ รัศมีการโคจรของอิเล็กตรอนสำหรับสถานะพื้นเท่ากับ $\frac{a}{9}$ (ตัวเลือกที่ 5)

2. อะตอมไฮโดรเจนเปลี่ยนระดับพลังงานจากสถานะที่ $n$ ไปยังสถานะพื้นที่มีพลังงาน $-13.6$ อิเล็กตรอนโวลต์ โดยแผ่รังสีที่มีพลังงาน $10.2$ อิเล็กตรอนโวลต์ ออกมา

คำถาม $n$ มีค่าเท่าใด [A-Level ฟิสิกส์ ปี 68]

เฉลยข้อสอบฟิสิกส์อะตอมข้อที่ 2

วิธีทำ จาก $E_1=-13.6\text{ eV}$ และ $E_n=-\frac{13.6}{n^2}\text{ eV}$

จะได้ว่า $E_n-E_1=10.2$

$-\frac{13.6}{n^2}-\left(-13.6\right)=10.2$

$-\frac{13.6}{n^2}=10.2-13.6$

$-\frac{13.6}{n^2}=-3.4$

$n^2=\frac{13.6}{3.4}$

$n^2=4$

$n=2$

ตอบ $n$ มีค่าเท่ากับ $2$

3. หากฉายคลื่นแม่เหล็กไฟฟ้าที่มีพลังงาน $4 \text{ eV}$ เข้าไปยังผิวโลหะ $x$ จะพบว่าสามารถเกิดกระแสไฟฟ้าในวงจรโฟโตอิเล็กทริกได้ และอิเล็กตรอนที่หลุดออกมาจะมีพลังงานจลน์สูงสุด $1.8\text{ eV}$ จงหาว่าถ้าให้พลังงานแสงที่มีความถี่เป็นครึ่งหนึ่งของกรณีแรก อิเล็กตรอนจะหลุดออกมาโดยมีพลังงานจลน์สูงสุดเท่าใด [แนว A-Level ฟิสิกส์ ปี 67]

$-0.2\text{ eV}$
$0.2\text{ eV}$
$0.8\text{ eV}$
$1.5\text{ eV}$
ไม่มีอิเล็กตรอนหลุดออกมาเลย

เฉลยข้อสอบฟิสิกส์อะตอมข้อที่ 3

วิธีทำ หาฟังก์ชันงานของโลหะ $x$
จาก $hf=W+E_{k_{max}}$
แทนค่า $4=W+1.8$
$W=2.2\text{ eV}$

ดังนั้น โลหะ $x$ มี $W=2.2\text{ eV}$

หาพลังงานของแสงในกรณีที่สอง $(f_2=\frac{f}{2})$
จาก $hf_2=\frac{hf}{2}$
$hf_2=\frac{4}{2}$
$hf_2=2\text{ J}$

ดังนั้น พลังงานของแสงในกรณีสองเท่ากับ $2\text{ J}$
หาพลังงานจลน์สูงสุด
จาก $hf=W+E_{k_{max}}$
แทนค่า $2=2.2+E_{k_{max}}$
$W=-0.2\text{ eV}$
ดังนั้น ติดลบแสดงว่า $hf<W$ จึงได้ว่าไม่มีอิเล็กตรอนหลุดออกมาเลย
ตอบ ไม่มีอิเล็กตรอนหลุดออกมาเลย (ตัวเลือกที่ 5)