สรุป คลื่น ฟิสิกส์ ม.5 พร้อมโจทย์และเฉลยฟรี

วันนี้พี่มีสรุปเนื้อหาวิชาฟิสิกส์ ม.5 เรื่อง “คลื่น” มาให้น้อง ๆ ได้อ่านกันด้วยน้าา โดยในบทความนี้จะกล่าวถึงความหมาย, ประเภท, ส่วนประกอบ, อัตราเร็วของคลื่น, พฤติกรรมของคลื่น เป็นต้น พร้อมแจกแบบฝึกหัดและเฉลยให้ไป
ลองทำท้ายบทความอีกด้วยย

สนใจหัวข้อไหน ... กดอ่านเลย

คลื่นคืออะไร ?

คลื่น (Wave) คือ การถ่ายทอดพลังงานจากแหล่งกำเนิดไปยังบริเวณรอบ ๆ ผ่านการสั่นหรือการรบกวนของตัวกลาง โดยที่อนุภาคของตัวกลางไม่ได้เคลื่อนที่ตามคลื่น แต่จะสั่นอยู่กับที่ และส่งต่อพลังงานไปยังอนุภาคข้างเคียง ทำให้เกิด
การเคลื่อนที่ของคลื่นจากจุดหนึ่งไปยังอีกจุดหนึ่ง

คลื่นมีกี่ประเภท ?

คลื่นสามารถแบ่งออกได้หลายประเภท ตามลักษณะต่าง ๆ ดังนี้

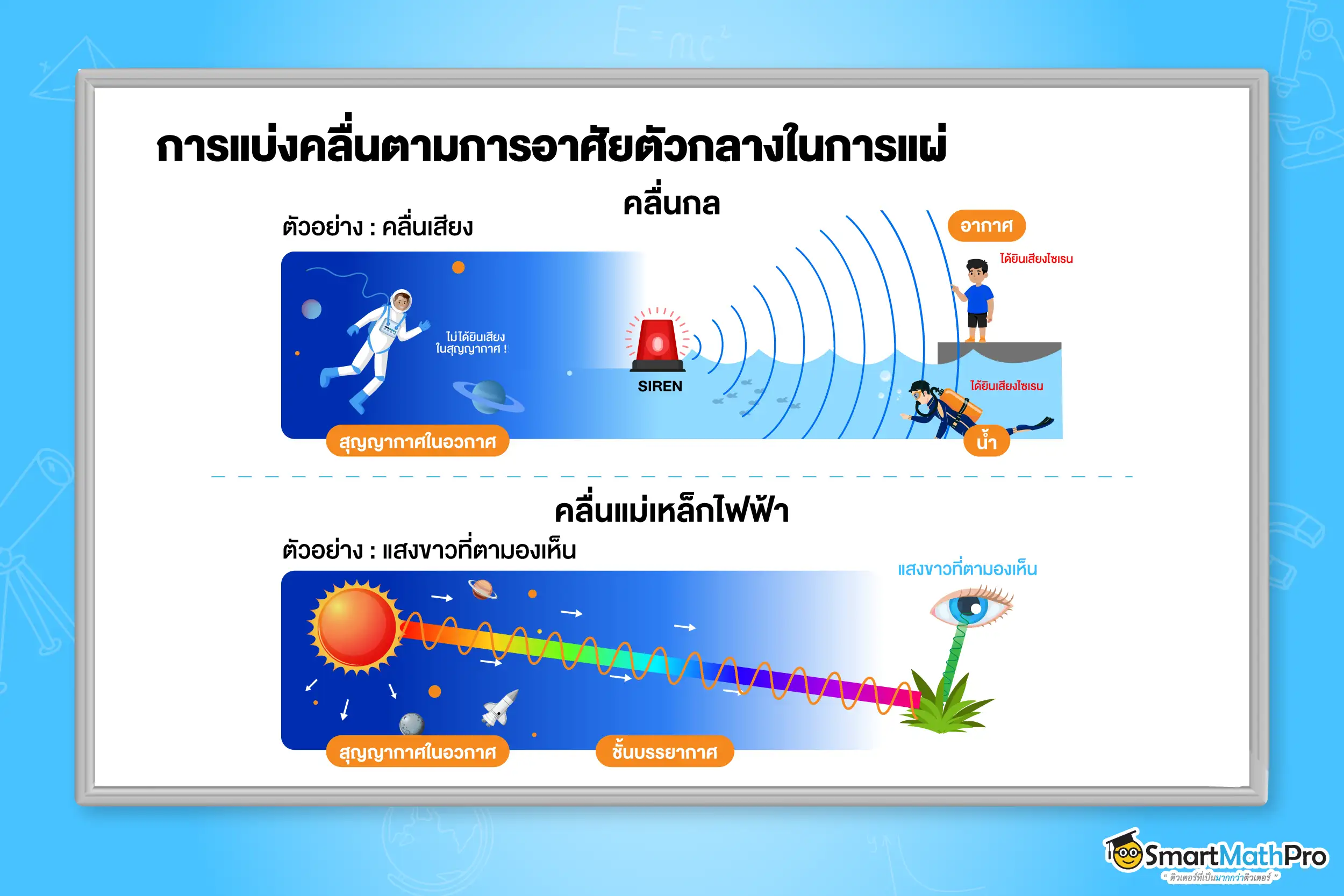
แบ่งตามการอาศัยตัวกลางในการแผ่ของคลื่น
- คลื่นกล (Mechanical Wave) เป็นคลื่นที่เคลื่อนที่โดยอาศัยตัวกลางซึ่งอาจเป็นของแข็ง ของเหลว หรือแก๊ส ก็ได้ เช่น คลื่นน้ำ, คลื่นในเส้นเชือก, คลื่นเสียง
- คลื่นแม่เหล็กไฟฟ้า (Electromagnetic Wave) เป็นคลื่นที่ไม่จำเป็นต้องอาศัยตัวกลางในการเคลื่อนที่ สามารถเคลื่อนที่ในสุญญากาศได้ มี 7 ชนิด คือ คลื่นวิทยุ, คลื่นไมโครเวฟ, รังสีอินฟราเรด, แสง, รังสีอัลตราไวโอเลต, รังสีเอกซ์, รังสีแกมมา

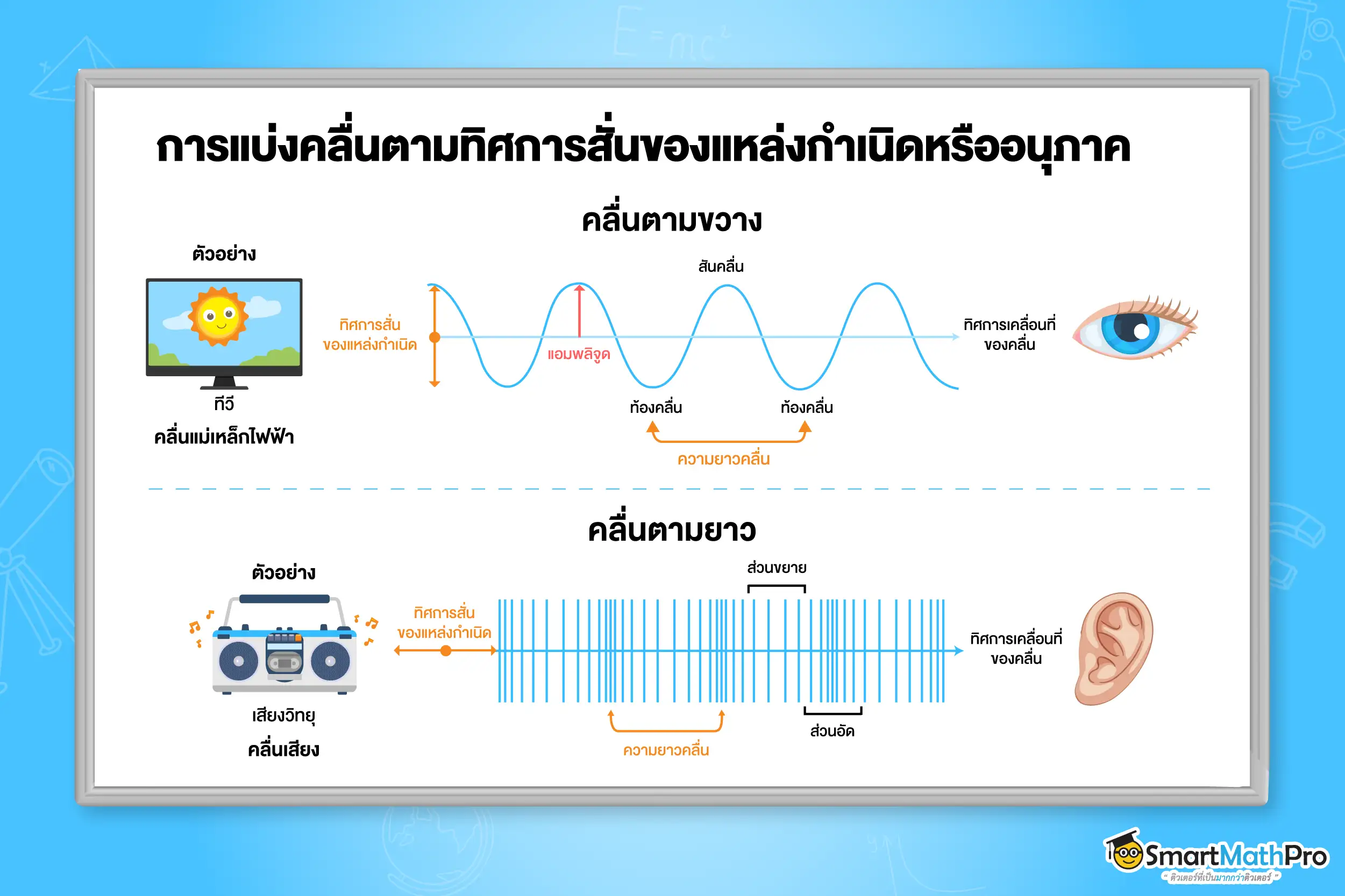
แบ่งตามทิศการสั่นของแหล่งกำเนิดหรืออนุภาค
- คลื่นตามขวาง (Transverse Wave) เป็นคลื่นที่มีทิศการสั่นของตัวกลางอยู่ในแนวตั้งฉากกับทิศการเคลื่อนที่ของคลื่น เช่น คลื่นผิวน้ำ, คลื่นในเส้นเชือก, คลื่นแม่เหล็กไฟฟ้าทุกชนิด
- คลื่นตามยาว (Longitudinal Wave) เป็นคลื่นที่อนุภาคของตัวกลางเคลื่อนที่ตามหรือขนานกับทิศ
  การเคลื่อนที่ของคลื่น เช่น คลื่นเสียง, คลื่นที่เกิดจากการอัดและขยายตัวในขดลวดสปริง

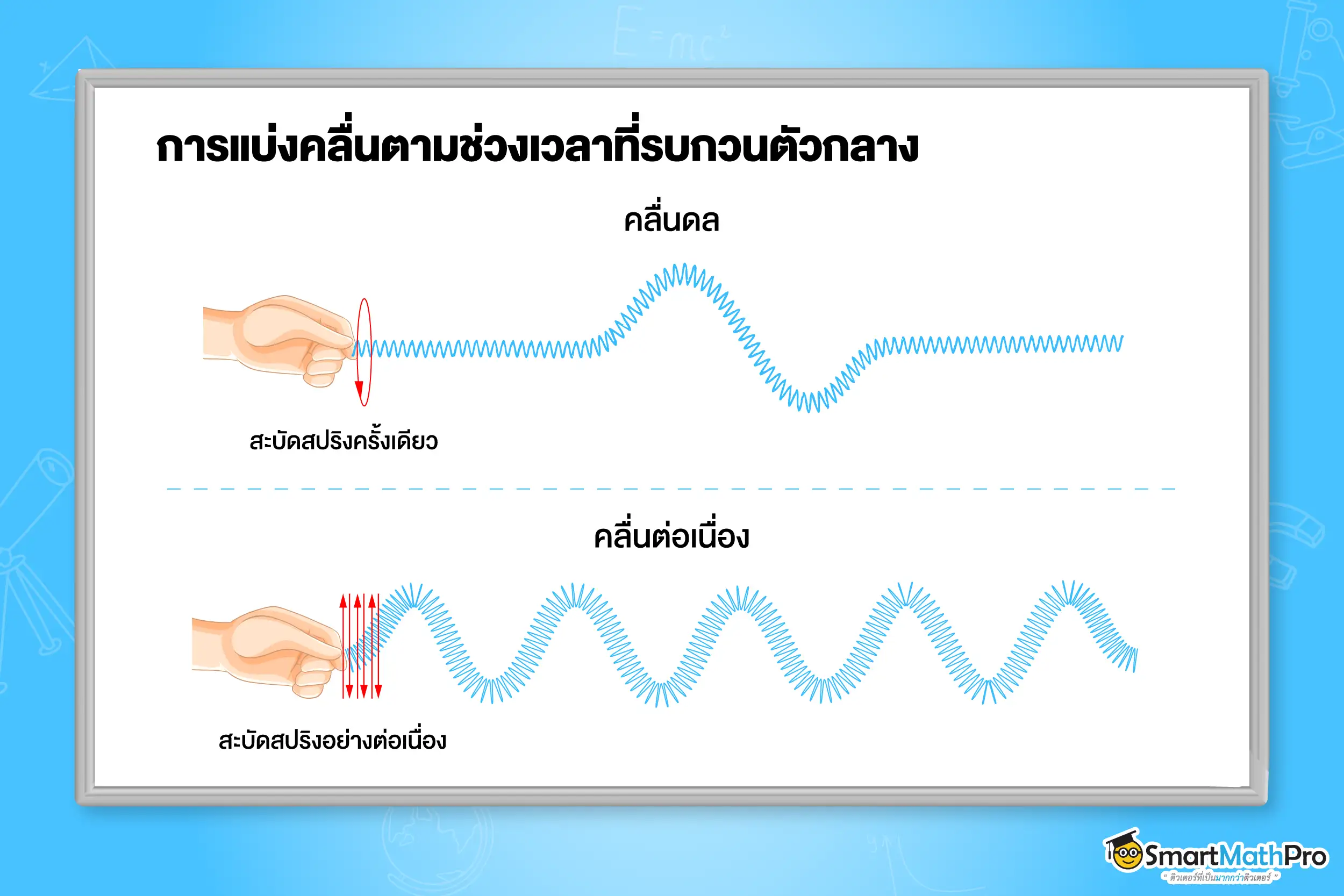
แบ่งตามช่วงเวลาที่รบกวนตัวกลาง
- คลื่นดล (Pulse Wave) เป็นคลื่นที่เกิดจากการรบกวนตัวกลางเป็นช่วงเวลาสั้น ๆ ทำให้เกิดคลื่นแผ่ออกไปจำนวนน้อยเพียง 1 หรือ 2 ลูกคลื่น เช่น การสะบัดปลายเชือกเพียงครั้งเดียว, การดีดสายกีตาร์
  เพียงครั้งเดียว
- คลื่นต่อเนื่อง (Continuous Wave) เป็นคลื่นที่เกิดจากเกิดจากการรบกวนตัวกลางอย่างต่อเนื่อง เกิดคลื่นแผ่ไปเป็นขบวนอย่างต่อเนื่อง เช่น การสะบัดปลายเชือกขึ้นลงสม่ำเสมอ, การดีดสายกีตาร์อย่างต่อเนื่อง

ตัวอย่างโจทย์เกี่ยวกับประเภทของคลื่น

คลื่นใดต่อไปนี้ เป็นคลื่นที่จำเป็นต้องอาศัยตัวกลางในการเคลื่อนที่
ก. คลื่นแสง ข. คลื่นเสียง ค. คลื่นผิวน้ำ
ข้อใดถูกต้อง

ทั้ง ก ข และ ค
ข้อ ข และ ค
ข้อ ก เท่านั้น
ผิดทุกข้อ

อธิบายเฉลยโจทย์เกี่ยวกับประเภทของคลื่น

ตอบ ตัวเลือก 2. ข้อ ข และ ค

วิธีทำ
วิเคราะห์ข้อ ก ข และ ค
คลื่นแสง $\to$ เป็นคลื่นแม่เหล็กไฟฟ้า ไม่จำเป็นต้องใช้ตัวกลาง
คลื่นเสียง $\to$ เป็นคลื่นกล ต้องอาศัยตัวกลาง (อากาศ น้ำ ของแข็ง)
คลื่นผิวน้ำ $\to$ เป็นคลื่นกล ต้องอาศัยตัวกลาง (น้ำ)

ส่วนประกอบของคลื่น

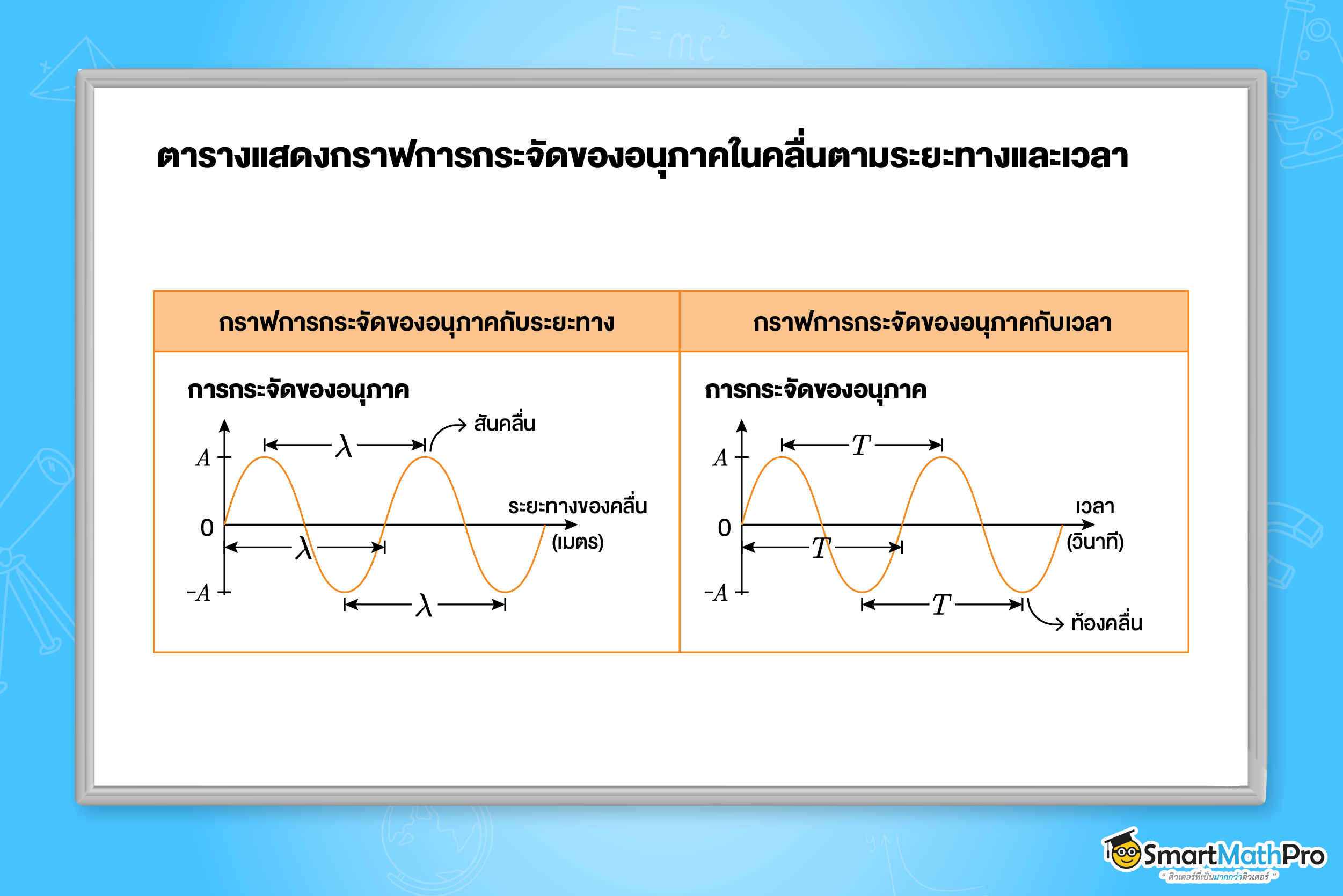
การทำความเข้าใจองค์ประกอบพื้นฐานของคลื่นจะช่วยให้เราเข้าใจธรรมชาติและการทำงานของคลื่นได้ดียิ่งขึ้น

สันคลื่นและท้องคลื่น (Crest and Trough)
- สันคลื่น คือ จุดที่คลื่นยกตัวขึ้นสูงสุด
- ท้องคลื่น คือ จุดที่คลื่นยุบตัวลงต่ำสุด
ความยาวคลื่น (Wavelength : $\lambda$ )
ความยาวคลื่น คือ ระยะทางที่คลื่นเคลื่อนที่ครบหนึ่งรอบพอดี ซึ่งเท่ากับระยะห่างระหว่างสันคลื่นที่อยู่ติดกัน
สองสัน หรือท้องคลื่นที่อยู่ติดกันสองท้อง
แอมพลิจูด (Amplitude : $A$ )
แอมพลิจูด คือ ขนาดของการกระจัดสูงสุดของอนุภาคตัวกลางจากตำแหน่งสมดุล ซึ่งเท่ากับระยะของคลื่นที่วัดจากแนวสมดุลไปถึงสันคลื่นหรือท้องคลื่น
ความถี่ (Frequency : $f$ )
ความถี่ คือ จำนวนรอบของคลื่นที่เคลื่อนที่ผ่านจุดใดจุดหนึ่งในหนึ่งหน่วยเวลา
คาบ (Period : $T$ )
คาบ คือ ช่วงเวลาที่คลื่นใช้ในการเคลื่อนที่ครบหนึ่งรอบพอดี คาบเป็นส่วนกลับของความถี่ โดยมีความสัมพันธ์กันดังนี้
สูตรความสัมพันธ์ระหว่างคาบและความถี่
$T=\frac{1}{f}$
โดยที่
$T$ คือ คาบ มีหน่วยเป็นวินาที $(s)$
$f$ คือ ความถี่ มีหน่วยเป็นเฮิรตซ์ $(Hz)$ หรือ รอบต่อวินาที $(s^{-1})$
เฟส (Phase)
เฟส คือ ตำแหน่งหรือสถานะของคลื่น ณ ขณะใดขณะหนึ่ง โดยปกติเราจะอ้างอิงเฟสเป็นมุมในวงกลมหนึ่งรอบ
( $0$ ถึง $360$ องศา หรือ $0$ ถึง $2\pi$ เรเดียน) จุดที่มีเฟสเดียวกันจะเคลื่อนที่ในทิศทางเดียวกันและมีขนาดการกระจัด
เท่ากัน เช่น สันคลื่นทุกจุดมีเฟสเดียวกัน และท้องคลื่นทุกจุดก็มีเฟสเดียวกัน

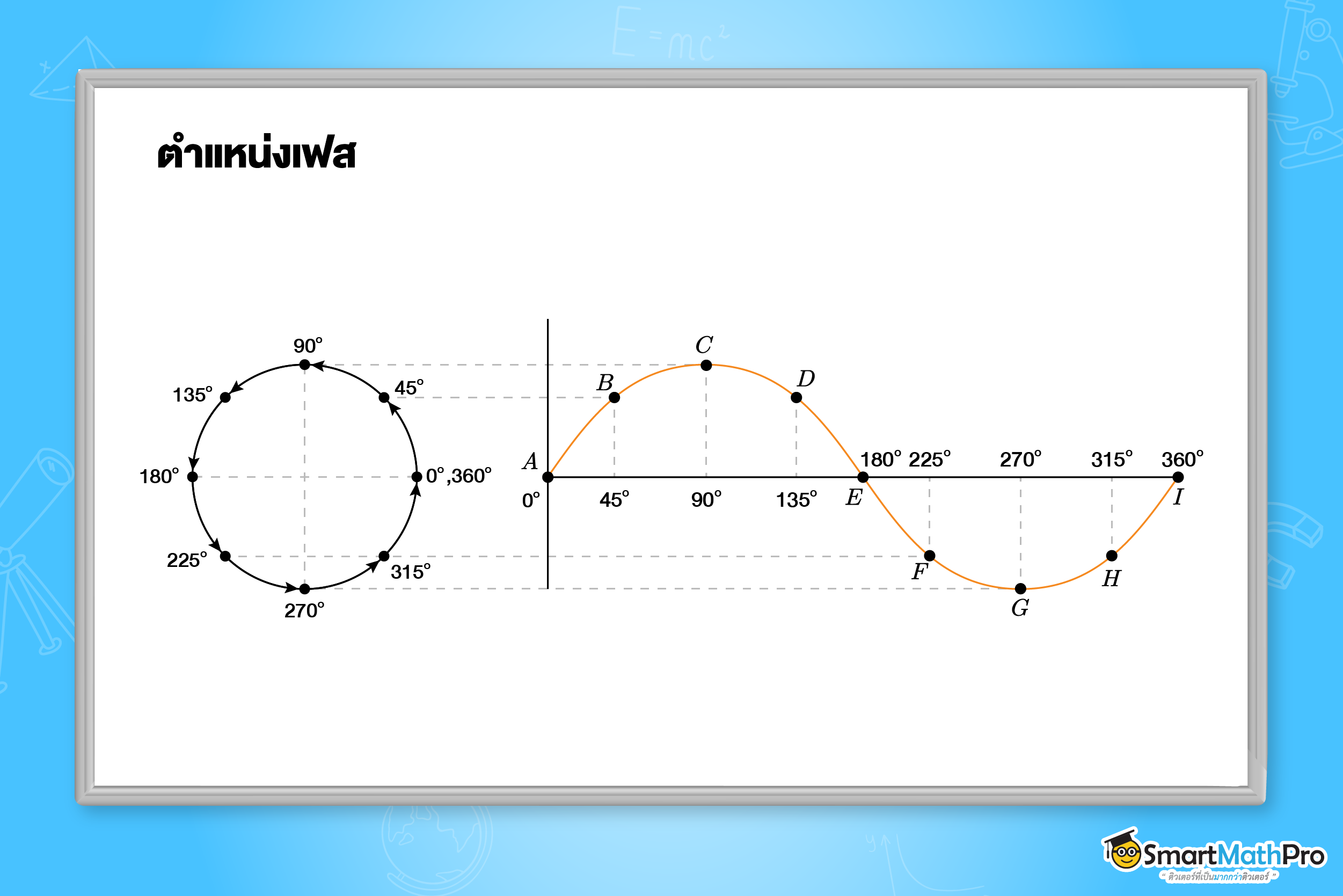
- เฟสตรงกัน
  เฟสตรงกัน คือ จุด 2 จุด บนคลื่นที่มีการกระจัดเท่ากัน และลักษณะการสั่นไปทางเดียวกัน ซึ่งมีเฟสที่เท่ากันหรือต่างกันเป็นจำนวนเต็มของรอบ (เช่น 0, 1, 2, 3… รอบ) เช่น จากภาพ จุด A และจุด I มีเฟสตรงกัน
- เฟสตรงข้ามกัน
  เฟสตรงข้ามกัน คือ จุด 2 จุด บนคลื่นที่มีการกระจัดเท่ากัน แต่มีตำแหน่งและทิศทางการสั่นตรงข้ามกัน ซึ่งมีเฟสที่ต่างกันครึ่งรอบ (เช่น $180$ องศา หรือ $\pi$ เรเดียน) เช่น จากภาพ จุด C และ จุด G มีเฟสตรงข้ามกัน
- ความต่างเฟส
  ความต่างเฟส คือ ผลต่างของเฟสระหว่างสองจุดบนคลื่นเดียวกัน หรือระหว่างคลื่นสองคลื่น ณ ขณะเวลาใดเวลาหนึ่ง

หน้าคลื่นและรังสี

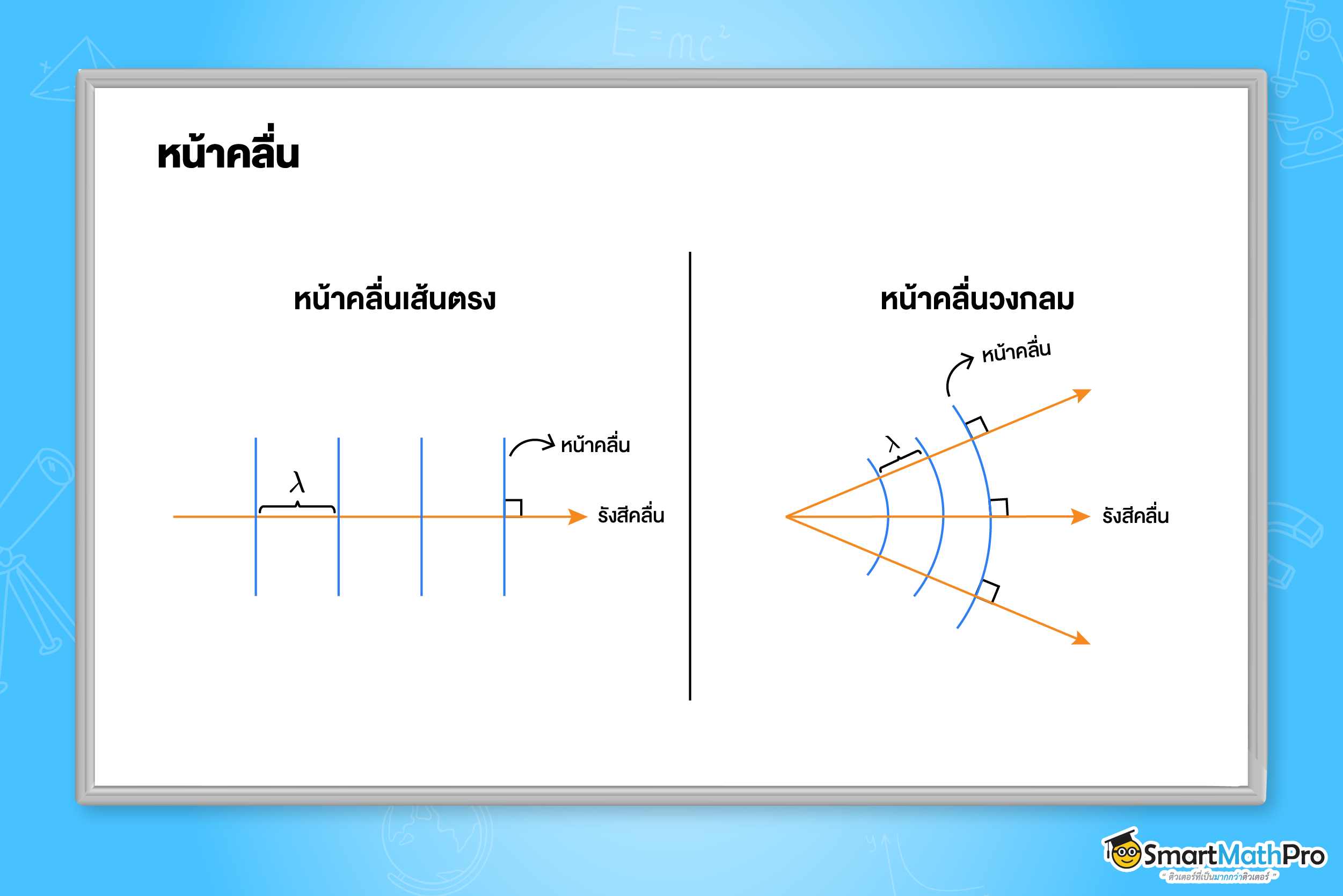
หน้าคลื่น คือ เส้นที่ลากตามแนวสันคลื่นหรือตามแนวท้องคลื่น (ระยะห่างระหว่างหน้าคลื่นจึงเท่ากับความยาวคลื่น) แบ่งออกเป็น 2 ประเภท ดังนี้
- หน้าคลื่นเส้นตรง มีลักษณะเป็นระนาบแบน เกิดจากแหล่งกำเนิดที่เป็นสันยาว
- หน้าคลื่นวงกลม มีลักษณะเป็นรูปวงกลม เกิดจากแหล่งกำเนิดแบบจุด

รังสีคลื่น คือ สัญลักษณ์ที่ใช้แสดงทิศการ เคลื่อนที่ของคลื่น ซึ่งมีทิศตั้งฉากกับหน้าคลื่น

ตัวอย่างโจทย์เกี่ยวกับส่วนประกอบของคลื่น

คลื่นลูกหนึ่งมีความยาวคลื่น $4$ เมตร และมีความถี่ $10$ เฮิรตซ์ จงหาความต่างเฟสระหว่างจุดสองจุดบนคลื่นนี้ที่อยู่ห่างกัน $2.5$ เมตร

อธิบายเฉลยโจทย์เกี่ยวกับส่วนประกอบของคลื่น

ตอบ ความต่างเฟสระหว่างจุดสองจุด มีค่าเท่ากับ $\frac{5\pi}{4}$ เรเดียน

วิธีทำ

หาความต่างเฟส
$\Delta \phi =\frac{2\pi\Delta x}{\lambda}$

$\Delta \phi =\frac{2\pi(2.5)}{4}$

$\Delta \phi =\frac{5\pi}{4}$ เรเดียน

อัตราเร็วคลื่น

อัตราเร็วคลื่น (wave speed) คือ ระยะทางที่คลื่นเคลื่อนที่ได้ในหนึ่งหน่วยเวลา มีหน่วยเป็น เมตรต่อวินาที $(m/s)$

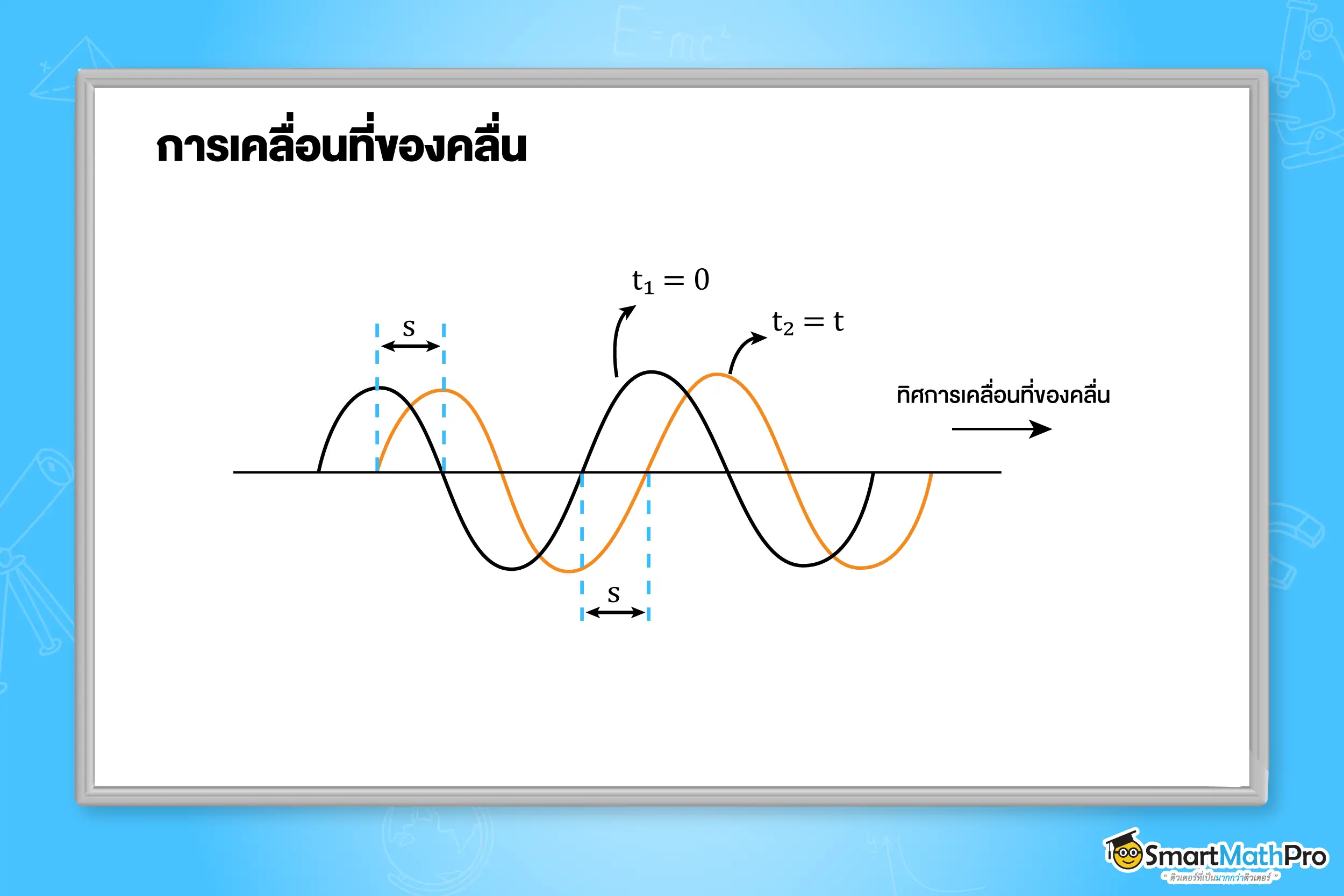
สูตรอัตราเร็วคลื่น

$v=\frac{s}{t}=\frac{\lambda}{T}=f\lambda$

โดยที่
$v$ คือ อัตราเร็วคลื่น มีหน่วยเป็น เมตรต่อวินาที $(m/s)$
$f$ คือ ความถี่ มีหน่วยเป็น เฮิรตซ์ $(Hz)$ หรือ รอบต่อวินาที $(s^{-1})$
$\lambda$ คือ ความยาวคลื่น มีหน่วยเป็น เมตร $(m)$

ตัวอย่างโจทย์เกี่ยวกับอัตราเร็วคลื่น

คลื่นเสียงความถี่ $500$ เฮิรตซ์ เคลื่อนที่ในอากาศด้วยความยาวคลื่น $0.68$ เมตร
อยากทราบว่าอัตราเร็วของคลื่นเสียงในอากาศ ณ ขณะนั้นมีค่าเท่าใด

อธิบายเฉลยโจทย์เกี่ยวกับอัตราเร็วคลื่น

ตอบ อัตราเร็วของคลื่นเสียงในอากาศ ณ ขณะนั้นมีค่าเท่ากับ $340$ เมตรต่อวินาที

วิธีทำ
หาอัตราเร็วคลื่น
$v=f\lambda$

$v=500(0.68)$

$v=340$ เมตรต่อวินาที

อัตราเร็วของคลื่นในตัวกลาง

เมื่อคลื่นเดินทางจากตัวกลางหนึ่งไปยังอีกตัวกลางหนึ่ง ความถี่ $(f)$ ของคลื่นจะคงที่เสมอ เพราะความถี่ถูกกำหนดโดยแหล่งกำเนิดคลื่น แต่อัตราเร็วคลื่น $(v)$ และความยาวคลื่น $(\lambda)$ จะเปลี่ยนแปลงไป เพื่อให้สอดคล้องกับคุณสมบัติของตัวกลางใหม่

อัตราเร็วคลื่นในเส้นเชือก

สูตรอัตราเร็วคลื่นในเส้นเชือก

$v=\sqrt{\frac{T}{\mu }}$

โดยที่

$v$ คือ อัตราเร็วคลื่นในเส้นเชือก มีหน่วยเป็น เมตรต่อวินาที $(m/s)$
$T$ คือ แรงตึงในเส้นเชือก มีหน่วยเป็น นิวตัน $(N)$
$\mu$ คือ มวลต่อความยาว มีหน่วยเป็น กิโลกรัมต่อเมตร $(kg/m)$

อัตราเร็วคลื่นในคลื่นผิวน้ำ
สูตรอัตราเร็วคลื่นในคลื่นผิวน้ำ

$v=\sqrt{gh}$

โดยที่

$v$ คือ อัตราเร็วคลื่นในคลื่นผิวน้ำ มีหน่วยเป็น เมตรต่อวินาที $(m/s)$
$g$ คือ ความเร่งเนื่องจากแรงโน้มถ่วง มีหน่วยเป็น เมตรต่อวินาทีกำลังสอง $(m/s^{2})$
$h$ คือ ความลึกของน้ำ มีหน่วยเป็น เมตร $(m)$
**สูตรนี้ใช้ได้ในกรณี $h$ ไม่ลึกมาก

ตัวอย่างโจทย์เกี่ยวกับอัตราเร็วของคลื่นในตัวกลาง

สระน้ำตื้นแห่งหนึ่งมีความลึก $0.2$ เมตร จงหาอัตราเร็วคลื่นที่ผิวน้ำเคลื่อนที่ในสระนี้ (กำหนดให้ $g=9.8 m/s^{2}$ )

อธิบายเฉลยโจทย์เกี่ยวกับอัตราเร็วของคลื่นในตัวกลาง

ตอบ อัตราเร็วคลื่นผิวน้ำที่เคลื่อนที่ในสระนี้มีค่าเท่ากับ $1.4$ เมตรต่อวินาที

วิธีทำ
หาอัตราเร็วคลื่นผิวน้ำ
$v=\sqrt{gh}$

$v=\sqrt{(9.8)(0.2)}$

$v=\sqrt{1.96}$

$v=1.4$ เมตรต่อวินาที

พฤติกรรมของคลื่น

พฤติกรรมของคลื่น คือ ปรากฏการณ์ต่าง ๆ ที่คลื่นแสดงออกมาเมื่อเคลื่อนที่ผ่านตัวกลาง หรือพบเจอสิ่งกีดขวาง ซึ่งเป็นคุณสมบัติพื้นฐานที่คลื่นทุกชนิดไม่ว่าจะเป็นคลื่นกล (เช่น คลื่นน้ำ คลื่นเสียง คลื่นในเส้นเชือก) หรือคลื่นแม่เหล็กไฟฟ้า (เช่น คลื่นแสง คลื่นวิทยุ) จะแสดงออกมาเหมือนกัน มี 4 พฤติกรรมหลัก ๆ ดังนี้

การสะท้อนของคลื่น (Reflection)

การสะท้อนของคลื่น คือ ปรากฏการณ์ที่คลื่นเคลื่อนที่ไปกระทบกับสิ่งกีดขวางแล้วสะท้อนกลับมาในตัวกลางเดิม เช่น คลื่นน้ำที่กระทบกำแพงแล้วสะท้อนกลับ หรือแสงที่ตกกระทบกระจกแล้วสะท้อนเข้าตาเรา

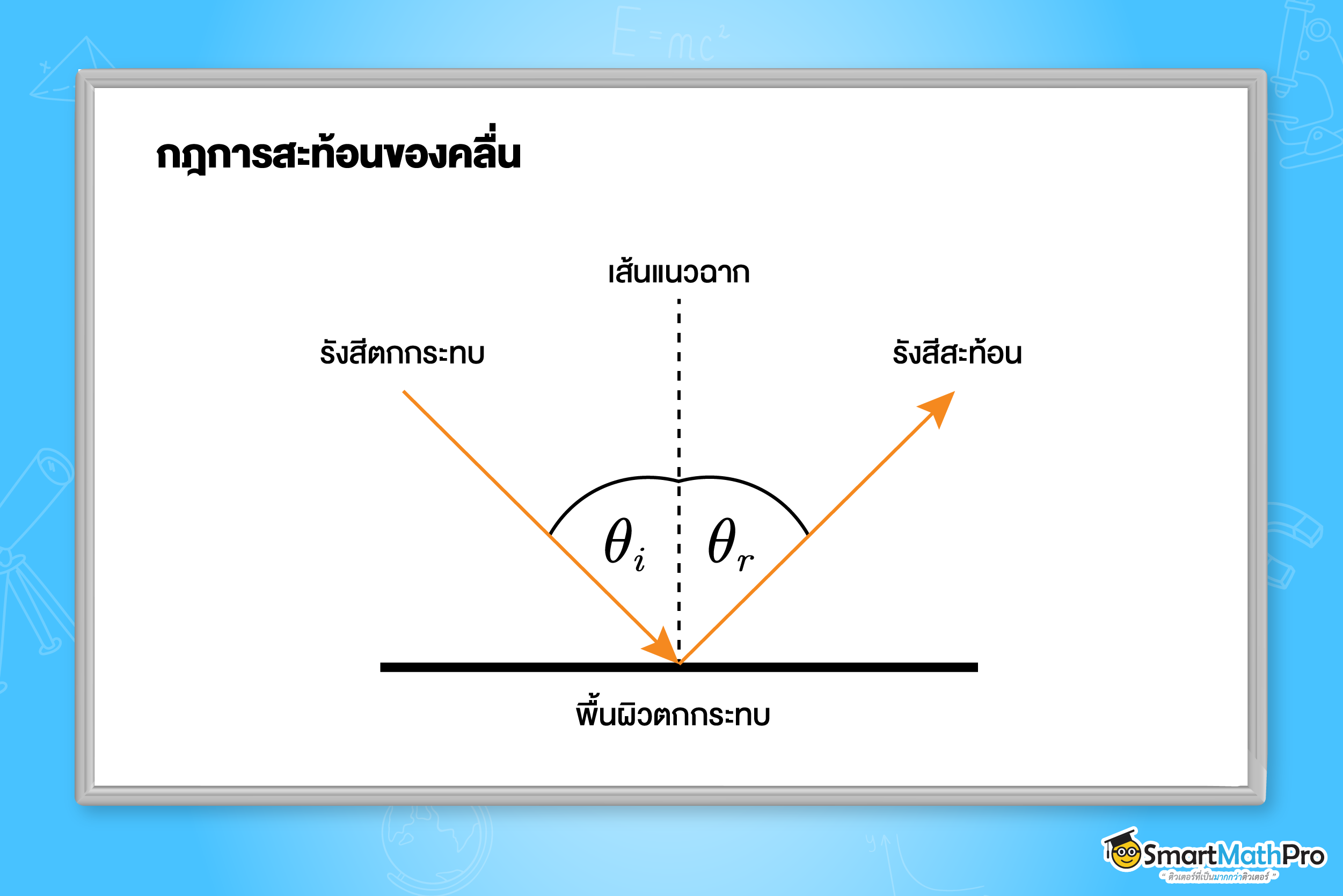
กฎการสะท้อนของคลื่น

รังสีตกกระทบ (Incident Ray), รังสีสะท้อน (Reflected Ray) และเส้นแนวฉาก (Normal Line) อยู่ในระนาบเดียวกัน
มุมตกกระทบ (Angle of Incidence: $\theta _{i}$ ) เท่ากับ มุมสะท้อน (Angle of Reflection: $\theta _{r}$ ) $\theta _{i}=\theta _{r}$

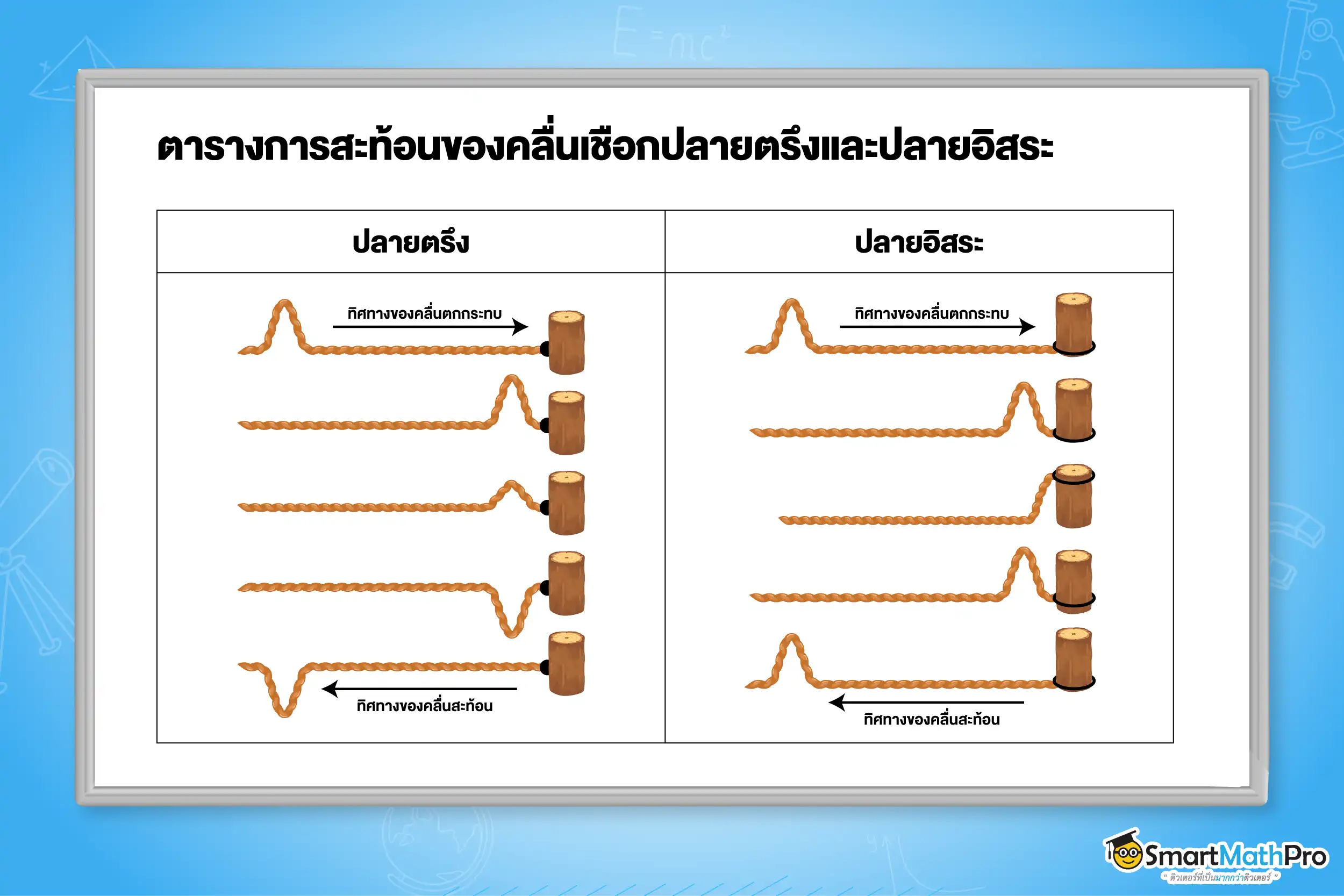
การสะท้อนของคลื่นในเส้นเชือก

เมื่อคลื่นในเส้นเชือกเดินทางไปชนปลายเชือกจะเกิดการสะท้อนกลับ แบ่งเป็น 2 กรณี

ปลายตรึง คลื่นสะท้อน กลับเฟส (เฟสเปลี่ยน $180$ องศา)
ปลายอิสระ คลื่นสะท้อน ไม่กลับเฟส (เฟสคงเดิม)

ตัวอย่างโจทย์เกี่ยวกับการสะท้อนของคลื่น

อธิบายเฉลยโจทย์เกี่ยวกับการสะท้อนของคลื่น

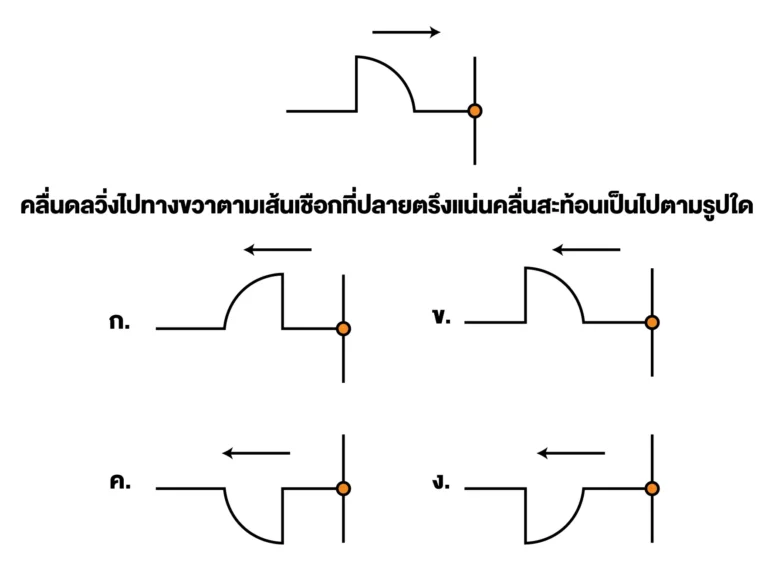
ตอบ ค.

วิธีทำ
ปลายตรึงแน่น
เมื่อคลื่นกระทบปลายตรึงแน่น จะเกิด การกลับเฟส
หมายความว่า ส่วนที่อยู่เหนือแนวสมดุล (สันคลื่น) จะกลายเป็นส่วนที่อยู่ใต้แนวสมดุล (ท้องคลื่น)
และส่วนที่อยู่ใต้แนวสมดุล (ท้องคลื่น) จะกลายเป็นส่วนที่อยู่เหนือแนวสมดุล (สันคลื่น) ดังนั้น ข้อ ก. และ ข. จึงไม่ถูกต้อง

ทิศทางการเคลื่อนที่กลับกัน
คลื่นที่สะท้อนจะวิ่งกลับในทิศทางตรงกันข้ามกับคลื่นตกกระทบ (จากขวาไปซ้าย) ดังนั้น ข้อ ง.
จึงไม่ถูกต้อง

การหักเหของคลื่น (Refraction)

การหักเหของคลื่น คือ ปรากฏการณ์ที่คลื่นเคลื่อนผ่านรอยต่อระหว่างตัวกลาง 2 ชนิด ที่แตกต่างกัน แล้วทำให้อัตราเร็วของคลื่นและความยาวคลื่นเปลี่ยนไป แต่ความถี่ของคลื่นยังคงเดิม โดยคลื่นจะเบนทิศของการเคลื่อนที่ไปจากเดิมหรือไม่ก็ได้

*ความรู้เพิ่มเติม* ในกรณีที่คลื่นตกกระทบโดยหน้าคลื่นตกกระทบขนานกับรอยต่อของตัวกลาง (มุมตกกระทบเท่ากับ $90$ องศา) คลื่นจะไม่เปลี่ยนทิศทาง

ตัวอย่างโจทย์เกี่ยวกับการหักเหของคลื่น

คลื่นน้ำเคลื่อนที่จากบริเวณน้ำลึกไปยังบริเวณน้ำตื้น ในบริเวณน้ำลึกหน้าคลื่นอยู่ห่างกัน $10$ เซนติเมตร ถ้าหน้าคลื่นตกกระทบทำมุมกับรอยต่อ $53$ องศา และหน้าคลื่นหักเหกับรอยต่อทำมุม $37$ องศา ความยาวคลื่นผิวน้ำในบริเวณน้ำตื้นจะเป็นเท่าใด

อธิบายเฉลยโจทย์เกี่ยวกับการหักเหของคลื่น

ตอบ ความยาวคลื่นน้ำในบริเวณน้ำตื้นเท่ากับ $0.075$ เมตร หรือ $7.5$ เซนติเมตร

วิธีทำ
กำหนดให้ บริเวณน้ำลึกเป็นตัวกลางที่ 1 และบริเวณน้ำตื้นเป็นตัวกลางที่ 2
ในบริเวณน้ำลึกหน้าคลื่นอยู่ห่างกัน $10$ เซนติเมตร หมายถึงความยาวคลื่นเท่ากับ $10$ เซนติเมตร

หาความยาวคลื่น
จากกฎของสเนลล์

$\frac{sin\theta _{1}}{sin\theta _{2}}=\frac{\lambda _{1}}{\lambda _{2}}$

$\frac{sin53^{\circ}}{sin37^{\circ}}=\frac{10\times 10^{-2}}{\lambda _{2}}$

$\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{10^{-1}}{\lambda _{2}}$

$\lambda _{2}=10^{-1}\times \frac{3}{4}$

$\lambda_{2}=0.075$

มุมวิกฤต (critical angle)

ถ้ามุมตกกระทบทำให้มุมหักเหมีค่าเป็น $90^{\circ}$ หรือรังสีหักเหอยู่ในแนวรอยต่อระหว่างตัวกลางพอดี เรียกมุมนี้ว่า มุมวิกฤต

ตัวอย่างโจทย์เกี่ยวกับมุมวิกฤต

ในการทดลองโดยใช้ถาดคลื่น พบว่าความเร็วของคลื่นในน้ำลึกเป็น $2$ เท่าของความเร็วในน้ำตื้น
ถ้าจะทำให้เกิดการสะท้อนกลับหมด คลื่นจะต้องเริ่มเคลื่อนที่จากบริเวณใด และมีมุมวิกฤตกี่องศา

อธิบายเฉลยโจทย์เกี่ยวกับมุมวิกฤต

ตอบ การสะท้อนกลับหมดจะเกิดขึ้นเมื่อคลื่นเริ่มเคลื่อนที่บริเวณน้ำตื้นไปสู่บริเวณน้ำลึก และมีมุมวิกฤต $30$ องศา

วิธีทำ
การสะท้อนกลับหมดจะเกิดขึ้นเมื่อคลื่นเคลื่อนที่บริเวณน้ำตื้นไปสู่บริเวณน้ำลึก (คลื่นเคลื่อนที่ไปสู่ตัวกลางที่มีความเร็วมากขึ้น)
กำหนดให้ บริเวณน้ำตื้นเป็นตัวกลางที่ 1 และบริเวณน้ำลึกเป็นตัวกลางที่ 2
หามุมวิกฤต
จากกฎของสเนลล์

$\frac{sin\theta _{c}}{sin90^{\circ}}=\frac{v_{1}}{v_{2}}$

$sin\theta_{c}=\frac{v_{1}}{2v_{1}}$

$sin\theta_{c}=\frac{1}{2}$

$\theta_{c}=30^{\circ}$

การแทรกสอดของคลื่น (Interference)

การแทรกสอดของคลื่น คือ ปรากฏการณ์ที่เกิดขึ้นเมื่อคลื่นตั้งแต่สองขบวนขึ้นไปเคลื่อนที่มาพบกันในตัวกลางเดียวกัน
*ความรู้เพิ่มเติม* แหล่งกำเนิดอาพันธ์ คือ คลื่นที่มีความถี่เท่ากัน และเฟสตรงกัน หรือเฟสต่างกันคงที่

โดยใช้หลักการรวมกันของคลื่น เมื่อมีคลื่นสองขบวนจากแหล่งกำเนิดสองแหล่งมาเจอกัน

$\to$ ตำแหน่งที่เกิดการเสริมกัน (สันคลื่นเจอสันคลื่น หรือ ท้องคลื่นเจอท้องคลื่น)
เรียกว่า ตำแหน่งปฏิบัพ (Antinode)

$\to$ ตำแหน่งที่เกิดการหักล้างกัน (สันคลื่นเจอท้องคลื่น) เรียกว่า ตำแหน่งบัพ (node)

เมื่อเกิดการแทรกสอดจากแหล่งกำเนิคลื่นอาพันธ์ $S_{1}$ และ $S_{2}$ ที่มีเฟสตรงกัน

แนวกึ่งกลางระหว่าง $S_{1}$ และ $S_{2}$ จะเป็นแนวที่มีการแทรกสอดแบบเสริมกัน หรือแนวปฏิบัพ $A_{0}$
แล้วจะสลับด้วยแนวบัพ แนวปฏิบัพ ทั้งสองข้างอย่างสมมาตร
เส้นที่ลากเชื่อมโยงจุดที่มีการแทรกสอดแบบเสริม เรียก แนวปฏิบัพ $A$
เส้นที่ลากเชื่อมโยงจุดที่มีการแทรกสอดแบบหักล้าง เรียก แนวบัพ $N$

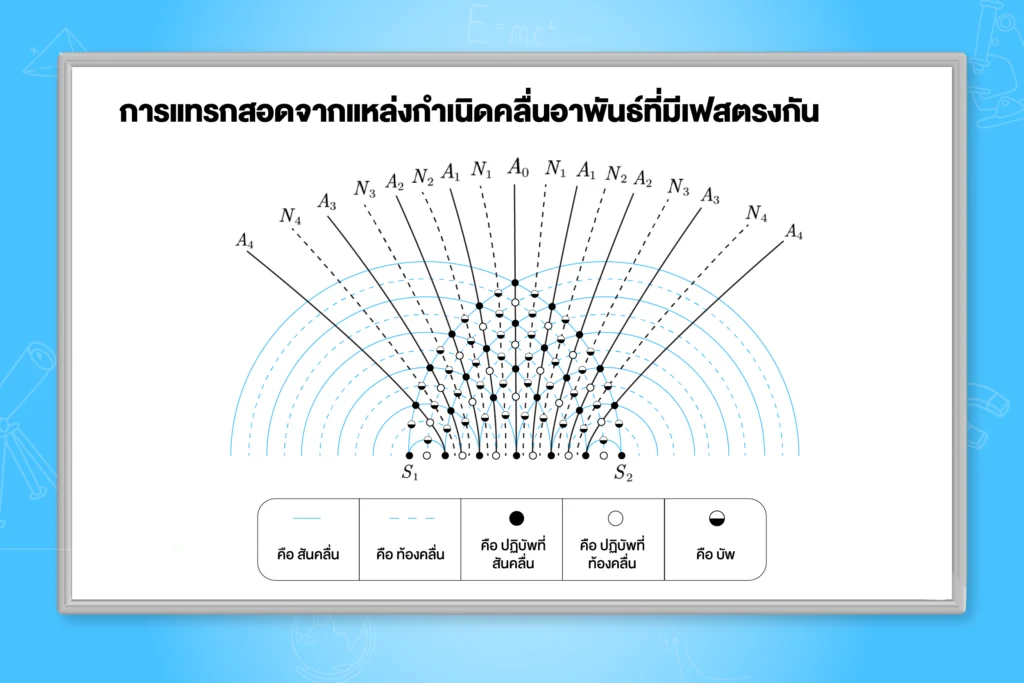
โดย
$P$ คือ จุดบนเส้นแนวปฏิบัพหรือบัพใด ๆ

$S_{1}P$ คือ ระยะจากแหล่งกำเนิดคลื่น $S_{1}$ ถึงจุด $P$ มีหน่วยเป็น เมตร $(m)$

$S_{2}P$ คือ ระยะจากแหล่งกำเนิดคลื่น $S_{2}$ ถึงจุด $P$ มีหน่วยเป็น เมตร $(m)$

$d$ คือ ระยะห่างระหว่างแหล่งกำเนิดคลื่น $S_{1}$ และ $S_{2}$ มีหน่วยเป็น เมตร $(m)$

$n$ คือ เลขของแนวปฏิบัพหรือบัพ

ตัวอย่างโจทย์เกี่ยวกับการแทรกสอด

1. $S_{1}$ และ $S_{2}$ เป็นแหล่งกำเนิดอาพันธ์เฟสตรงกัน จุด $P$ ห่างจาก $S_{1}$ และ $S_{2}$ เป็นระยะ $5$ เซนติเมตร และ $7$ เซนติเมตร ตามลำดับ ถ้าแหล่งกำเนิดคลื่นทั้งสองมีความความยาวคลื่น $2$ เซนติเมตร การแทรกสอดที่จุด $P$ อยู่บนแนวบัพหรือปฏิบัพที่เท่าไร

อธิบายเฉลยโจทย์เกี่ยวกับการแทรกสอด

ตอบ จุด $P$ อยู่บนแนวปฏิบัพที่ $1$

วิธีทำ
แหล่งกำเนิดอาพันธ์เฟสตรงกัน แนวกึ่งกลางระหว่าง $S_{1}$ และ $S_{2}$ จะเป็นแนวที่มีการแทรกสอดแบบเสริมกัน หรือแนวปฏิบัพ $A_{0}$

หาแนวปฏิบัพ $A$ ที่จุด $P$
จากสูตร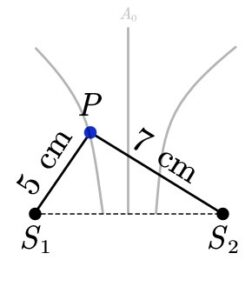

$\left |S_{1}P-S_{2}P\right |=n\lambda$
$\left |(5\times 10^{-2})-(7\times 10^{-2})\right |=n(2\times 10^{-2})$

$2\times 10^{-2}=(2\times 10^{-2})n$

$n=1$

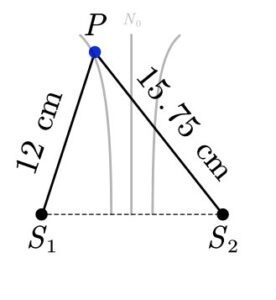
2. แหล่งกำเนิดอาพันธ์ $2$ แหล่ง ห่างกัน $10$ เซนติเมตร ให้คลื่นมีความยาวคลื่น $2.5$ เซนติเมตร เฟสตรงข้ามกัน จุด $P$ อยู่ห่างจากแหล่งกำเนิดทั้งสอง เป็นระยะ $12$ เซนติเมตร และ $15.75$ เซนติเมตร ตำแหน่งต่อไปนี้ อยู่บนแนวบัพหรือปฏิบัพที่เท่าใด

อธิบายเฉลยโจทย์เกี่ยวกับการแทรกสอด

ตอบ จุด $P$ อยู่บนแนวปฏิบัพที่ $2$

วิธีทำ

แหล่งกำเนิดอาพันธ์เฟสตรงข้ามกัน แนวกึ่งกลางระหว่าง $S_{1}$ และ $S_{2}$ จะเป็นแนวที่มีการแทรกสอดแบบหักล้างกัน หรือแนวบัพ $N_{0}$

หาแนวบัพ $N$ ที่จุด $P$
จากสูตร

$\left |S_{1}P-S_{2}P\right |=n\lambda$

$\left |12-15.75\right |=n(2.5)$
$3.75=2.5n$
$n=1.5$
เนื่องจาก ค่า $n$ ไม่เป็นจำนวนเต็ม แสดงว่าจุด $P$ ไม่อยู่บนแนวบัพ $N$
ดังนั้น สามารถหาแนวปฏิบัพ $A$ ที่จุด $P$

จากสูตร
$\left |S_{1}P-S_{2}P\right |=(n-\frac{1}{2})(\lambda )$

$\left |12-15.75\right |=(n-\frac{1}{2})(2.5)$

$1.5=n-\frac{1}{2}$

$n=2$

คลื่นนิ่ง (Standing wave)

คลื่นนิ่งเกิดขึ้นเมื่อมีคลื่นสองขบวน จากแหล่งกำเนิดอาพันธ์สองแหล่ง เดินทางสวนกัน แล้วเกิดการรวมกันโดยเราจะเรียกคลื่นนิ่งเป็น loop

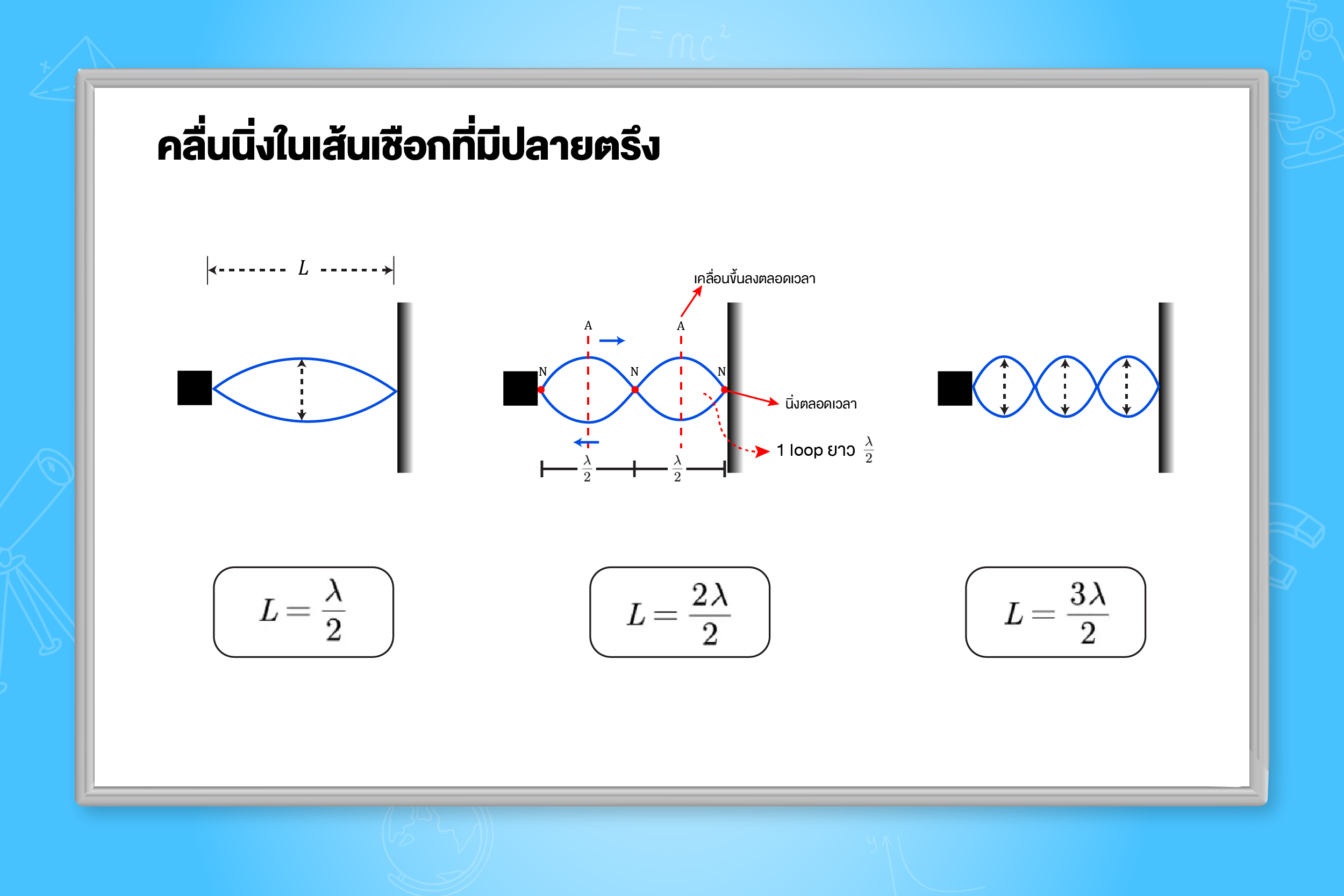
เราเรียกความถี่ของการสั่นที่ทำให้เกิด 1 loop ว่า ความถี่มูลฐาน หรือความถี่ฮาร์มอนิกที่ 1 ถ้าเราเพิ่มความถี่ของ
การสั่นเป็น 2 เท่าของความถี่มูลฐาน จะมี loop การสั่นเพิ่มเป็น 2 loop เรียกความถี่ดังกล่าวว่าความถี่ฮาร์มอนิกที่ 2

ตัวอย่างโจทย์เกี่ยวกับคลื่นนิ่ง

คลื่นในเส้นเชือกเคลื่อนที่ด้วยอัตราเร็ว $1$ เมตรต่อวินาที ไปยังอีกด้านหนึ่งที่ถูกยึดแน่นไว้ แล้วสะท้อนกลับเกิดเป็นคลื่นนิ่งดังรูป ถ้าเชือกนี้ยาว $8$ เมตร คลื่นจะมีความถี่กี่รอบต่อวินาที

อธิบายเฉลยโจทย์เกี่ยวกับคลื่นนิ่ง

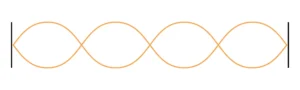
ตอบ คลื่นจะมีความถี่ $0.25$ รอบต่อวินาที

วิธีทำ

จากภาพจะเห็นว่าความยาว $8$ เมตร มีคลื่นนิ่งอยู่ทั้งหมด $4$ loop สามารถนับได้ว่าคลื่นนิ่งในเส้นเชือกนี้ประกอบ ด้วย $2$ ความยาวคลื่นเต็มพอดี

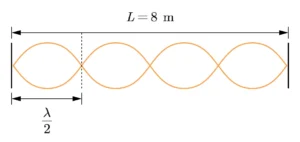
หาความยาวคลื่น
จากสูตร

$L=\frac{4\lambda }{2}$

$8=\frac{4\lambda }{2}$

$8=2\lambda$

$\lambda =4 m$

เมื่อทราบความยาวคลื่นในเส้นเชือกจะสามารถ

หาความถี่ของคลื่น
จากสูตร

$v=f\lambda$

$1=f(4)$

$f=\frac{1}{4}$

$f=0.25 Hz$

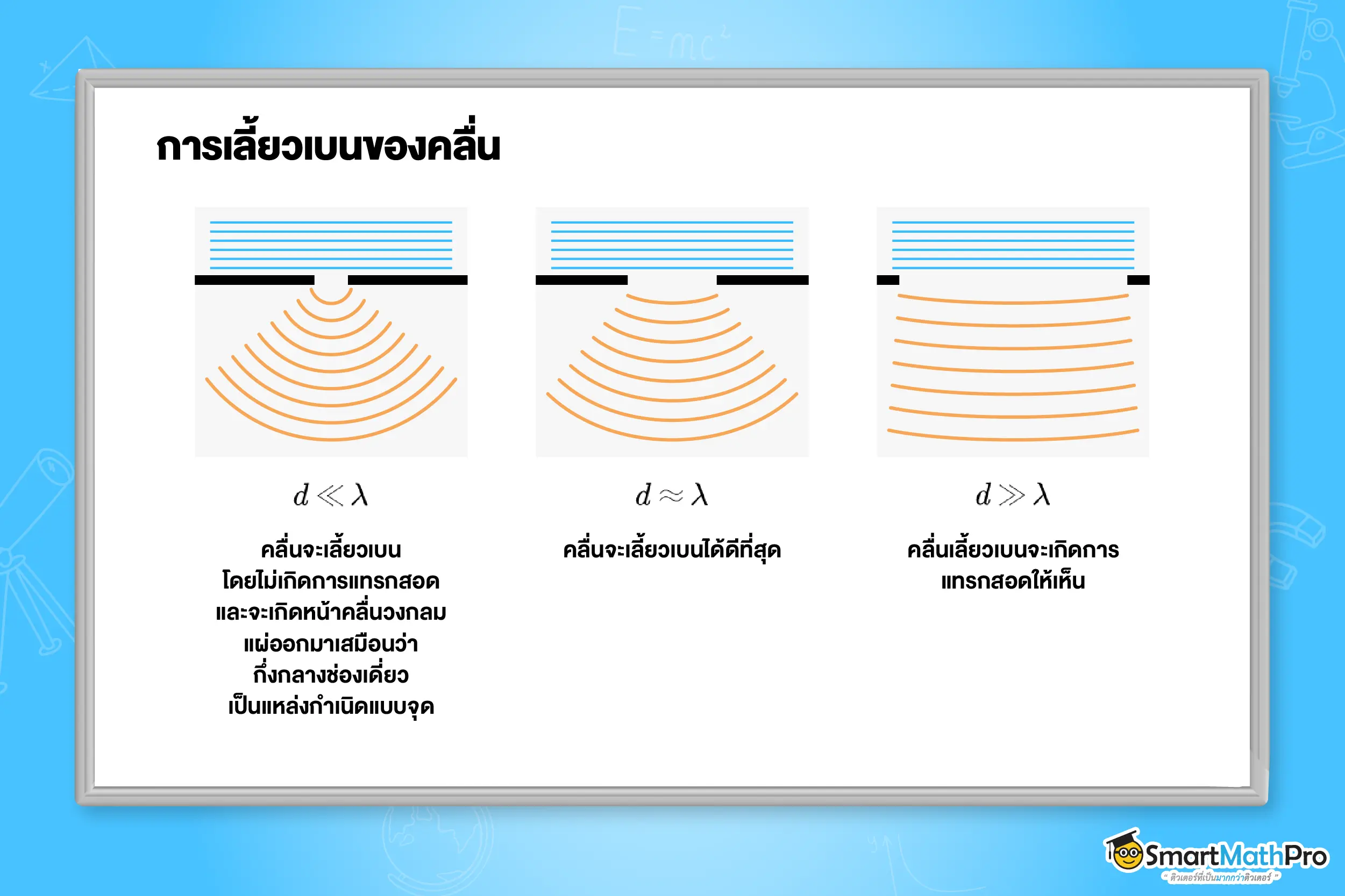
การเลี้ยวเบนของคลื่น (Diffraction)

การเลี้ยวเบนของคลื่น คือ ปรากฏการณ์ที่คลื่นสามารถเคลื่อนที่ผ่านสิ่งกีดขวางในตัวกลางเดียวกัน แล้วสามารถเลี้ยวอ้อมผ่านสิ่งกีดขว้างนั้นไปได้

การเลี้ยวเบนอธิบายโดยหลักของฮอยเกนส์ (Huygens’ Principle) ซึ่งกล่าวว่าแต่ละจุดบนหน้าคลื่นถือได้ว่าเป็นจุดกำเนิดคลื่นวงกลมใหม่ ที่มีเฟสและความยาวคลื่นเดียวกันออกไป

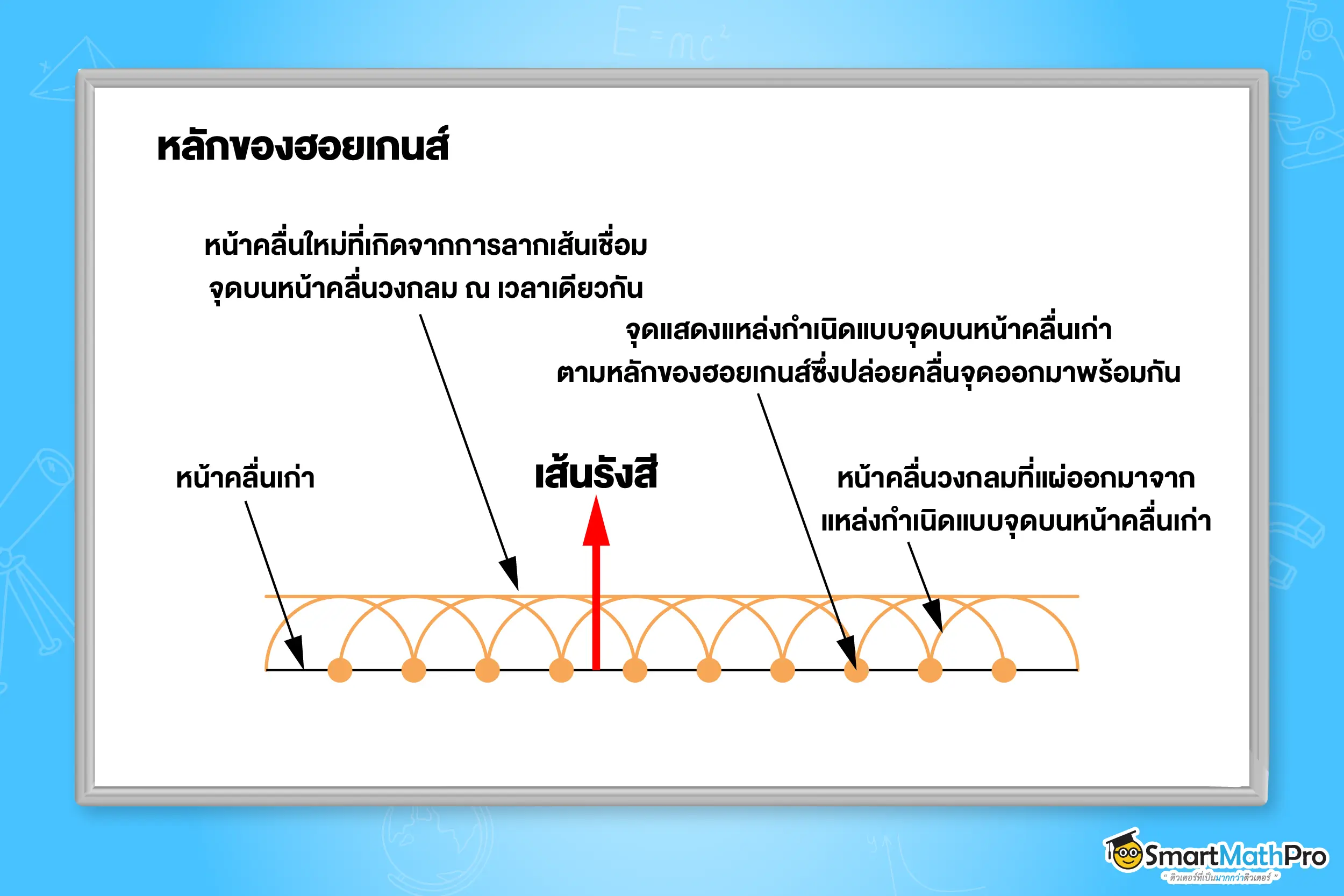
เมื่อคลื่นเคลื่อนที่มาถึงบริเวณที่มีสิ่งกีดขวาง ตรงจุดที่เป็นขอบของสิ่งกีดขวาง คลื่นจะเปลี่ยนทิศทางการเคลื่อนที่
อ้อมขอบของสิ่งกีดขวางไปด้านหลังของสิ่งกีดขวางได้โดยทิศทางของการเคลื่อนที่จะเปลี่ยนไปและแอมพลิจูดของคลื่นที่อ้อมไปนั้นมีค่าน้อยลง แต่ความยาวคลื่นกับความถี่ยังคงเท่าเดิมและสามารถเกิดการแทรดสอดของคลื่นที่ด้านหลัง
สิ่งกีดขวางได้

เก็บเนื้อหา A-Level ฟิสิกส์ให้แม่นกับ SmartMathPro

สำหรับสนามสอบ A-Level ก็จะเป็นอีกสนามที่มีความสำคัญมากเพราะสามารถใช้ยื่นคะแนนได้หลายคณะและเป็นวิชาที่ต้องอาศัยการเตรียมตัวค่อนข้างนาน สำหรับใครที่กลัวเตรียมตัวไม่ทันอยากจะประหยัดเวลาในการเตรียมสอบ

พี่ขอแนะนำคอร์สเรียนพิเศษสนาม A-Level ของ SmartMathPro ที่มีทั้ง A-Level คณิต 1,2 /
A-Level ภาษาอังกฤษ / A-Level ฟิสิกส์ / A-Level ภาษาไทย / A-Level สังคม เลยน้าา

โดยสำหรับใครที่ไม่มีพื้นฐานก็สามารถเรียนได้ เพราะพี่สอนตั้งแต่ปูพื้นฐาน ไปจนถึงพาทำโจทย์ตั้งแต่ระดับง่ายไปจนถึงความยากใกล้เคียงกับข้อสอบจริงเลย แถมมีเทคนิคในการทำข้อสอบอีกเพียบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้น > <

และสำหรับใครที่ยังไม่เริ่ม เริ่มติวตอนนี้ก็ยังทันน้าา แอบกระซิบว่าถ้าสมัครคอร์สตั้งแต่ตอนนี้พี่มี Unseen Mock Test ชุดพิเศษ 1 ชุด แถมฟรีไปให้ลองทำพร้อมสิทธิพิเศษประจำเดือนอีกมากมายด้วย ถ้าน้อง ๆ คนไหนสนใจคอร์สเตรียมสอบ A-Level สามารถ คลิก เข้ามาดูรายละเอียดได้เลยย

ข้อสอบเรื่องคลื่นพร้อมเฉลย

อธิบายเฉลยข้อสอบเกี่ยวกับคลื่น

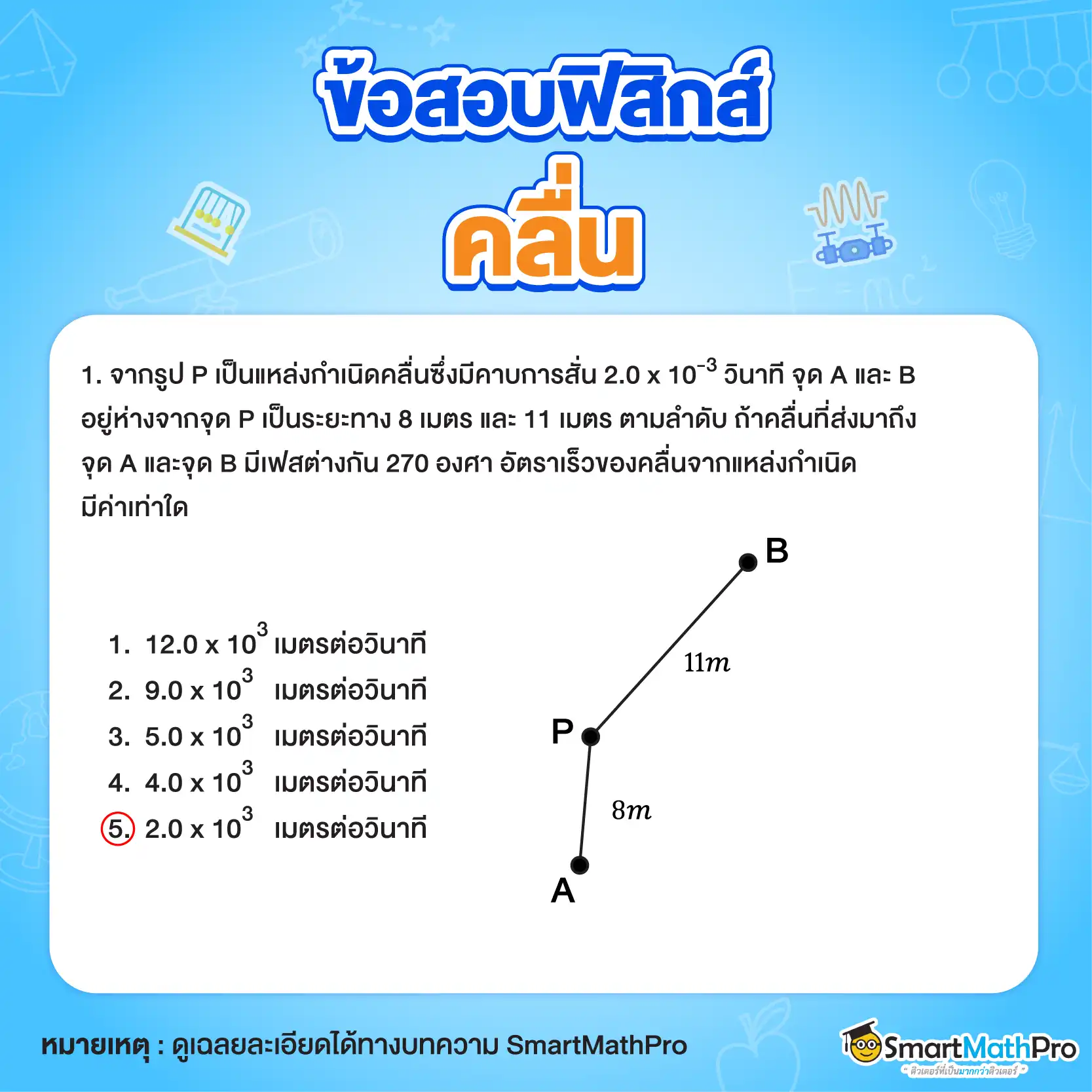
ตอบ ตัวเลือก 5. อัตราเร็วของคลื่นจากแหล่งกำเนิดมีค่าเท่ากับ $2\times 10^{3}$ เมตรต่อวินาที

วิธีทำ

หาความยาวคลื่น
$\Delta \phi =\frac{360\Delta x}{\lambda}$

$270=\frac{360(11-8)}{\lambda}$

$\lambda =\frac{360(3)(2)}{270}$
$\lambda =4 m$

หาอัตราเร็วของคลื่น
$v=f\lambda$

$v=\frac{\lambda }{T}$

$v=\frac{4}{2\times 10^{-3}}$

$v=2\times 10^{3}$ เมตรต่อวินาที

อธิบายเฉลยข้อสอบเกี่ยวกับคลื่น

ตอบ ตัวเลือก 1. $30\sqrt{2}$

วิธีทำ

กำหนดให้ บริเวณน้ำลึกเป็นตัวกลางที่ 1 และบริเวณน้ำตื้นเป็นตัวกลางที่ 2 จากกฎของสเนลล์จะได้

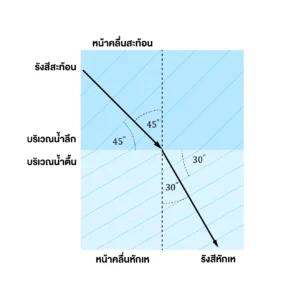
$\frac{sin\theta _{1}}{sin\theta _{2}}=\frac{v_{1}}{v_{2}}$

$\frac{sin45^{\circ}}{sin30^{\circ}}=\frac{60}{v_{2}}$

$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}=\frac{60}{v_{2}}$

$v_{2}=\frac{60}{\sqrt{2}}$

$v_{2}=\frac{60}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}$

$v_{2}=\frac{60\sqrt{2}}{2}$

$v_{2}=30\sqrt{2} m/s$

เป็นอย่างไรกันบ้างกับ “สรุปเนื้อหาเรื่อง คลื่น ฟิสิกส์ ม.5” และแนวข้อสอบที่พี่นำมาฝากในวันนี้ แนะนำว่าถ้าใครอยากจะแม่นเนื้อหาเรื่องนี้ นอกจากก็อ่านเนื้อหาแล้ว ก็ควรทบทวนอย่างเป็นประจำและฝึกทำแบบฝึกหัดเยอะ ๆ เพื่อให้เข้าใจ
มากขึ้นด้วยน้าา